Additive predictions of aboveground stand biomass in commercial logs and harvest residues for rotation age Pinus radiata plantations in New South Wales, Australia

Xixi Qiao · Huiquan Bi · Yun Li ·Fabiano Ximenes · Christopher J. Weston ·Liubov Volkova · Mohammad Reza Ghaf fariyan

Abstract Two systems of additive equations were developed to predict aboveground stand level biomass in log products and harvest residue from routinely measured or predicted stand variables for Pinus radiata plantations in New South Wales, Australia. These plantations were managed under three thinning regimes or stand types before clear-felling at rotation age by cut-to-length harvesters to produce sawlogs and pulpwood. The residue material following a clear-fell operation mainly consisted of stumps,branches and treetops, short of f-cut and waste sections due to stem deformity, defects, damage and breakage. One system of equations did not include dummy variables for stand types in the model specif ication and was intended for more general use in plantations where stand density management regimes were not the same as the stand types in our study.The other system that incorporated dummy variables was for stand type-specif ic applications. Both systems of equations were estimated using 61 plot-based estimates of biomass in commercial logs and residue components that were derived from systems of equations developed in situ for predicting the product and residue biomass of individual trees. To cater for all practical applications, two sets of parameters were estimated for each system of equations for predicting component and total aboveground stand biomass in fresh and dry weight respectively. The two sets of parameters for the system of equations without dummy variables were jointly estimated to improve statistical ef ficiency in parameter estimation. The predictive performances of the two systems of equations were benchmarked through a leave-one-plot-out cross validation procedure. They were generally superior to the performance of an alternative two-stage approach that combined an additive system for major components with an allocative system for sub-components. As using forest harvest residue biomass for bioenergy has increasingly become an integrated part of forestry, reliable estimates of product and residue biomass will assist harvest and management planning for clear-fell operations that integrate cut-to-length log production with residue harvesting.

Keywords Plot-based biomass estimates · Wood product · Harvest residue · Bioenergy · Systems of additive and allocative equations · Prediction error variance functions

Introduction

Pinus radiata(D. Don) is a versatile, fast-growing, mediumdensity softwood species native to a very limited natural range along the Californian central coast and to two Mexican islands of f Baja California (Lavery and Mead 1998; Rogers 2004; Rogers et al. 2006; Mead 2013). Following its introduction and domestication elsewhere in the world over much of the last century (Burdon et al. 2017), it has been transformed from an agroforestry, landscaping, ornamental and Christmas tree species that has little economic importance within its home countries to a major softwood plantation species outside of its native range with much improved growth performance and responsiveness to management and cultivation (Lewis et al. 1993; Rogers 2004; Mead 2013).Now it is the most extensively planted exotic coniferous species over four continents in the Southern Hemisphere. With a total worldwide area exceeding 4.3 million hectares and expanding (Mead 2013; Burdon et al. 2017),Pinus radiataplantations are the mainstay of the forest economy in Australia, Chile, New Zealand, Spain and South Africa, serving domestic markets and generating income from export (Lewis et al. 1993; Lavery and Mead 1998; Toro and Gessel 1999;Turner et al. 1999). The harvested wood has a wide range of end-uses such as structural sawtimber, board products,veneer, pulp, reconstituted wood, posts and poles. The harvesting and wood processing residues are increasingly used for bioenergy generation (Acuña et al. 2010; Mead 2013;Burdon et al. 2017; Ghaf fariyan et al. 2017; Lock and Whittle 2018; Van Holsbeeck et al. 2020).

Following New Zealand and Chile, Australia is the third largestP. radiatagrower with a current plantation estate of more than 0.77 million ha (Downham and Gavran 2019).About one-third of this resource is in the State of New South Wales (NSW) where the f irst commercial plantation was established about a century ago (Horne 1988). Since then,the practice ofP. radiataplantation silviculture has evolved continuously as plantation areas further expanded to cover an increasing range of site qualities and previous land-uses(Horne 1988; Turner et al. 2001). For plantations established in the 1980s and later, the practice has generally been to set the initial planting stocking to 1000 − 1300 trees/ha, except for steeper slopes where stands are established with a lower stocking of 700 − 900 trees/ha and no thinning operations are intended (Anon. 2016). For more productive sites,either one or two thinnings are prescribed to reduce stocking down to 450 − 550 trees/ha at the age of f irst thinning around 14 years and down to 200 − 300 trees/ha at the age of second thinning around 23 years (D. Watt, pers. comm.).Although experiments with more than two thinnings have been reported (Horne and Robinson 1988), the practice has not been adopted in plantation management. The decision to thin a particular area is also dependent on other factors such as drought exposure, tree health, customer product requirements, and economic and market considerations (Anon.2016). For poorer sites, no thinning is specif ied before the f inal harvest at the typical rotation age of 30 to 35 years. All thinnings and f inal harvesting are now routinely carried out by cut-to-length (CTL) harvesters as the CTL technology has been widely adopted by harvesting companies and contractors across Australia since its introduction to the country in the early 1990s (Priddle 2005; Lu et al. 2018; Shan et al.2021). This technology processes trees at the stump through a combination of harvester and forwarder. It leaves short of f-cut and waste sections, branches and unprocessed tree tops on site, yielding higher levels of residue than traditional whole-tree harvesting (Ghaf fariyan et al. 2012, 2015; Ghaffariyan and Apolit 2015).

The continuous harvesting of rotation ageP. radiataplantations throughout the year as determined through yield scheduling in NSW provides a sustained steady f low of commercial logs and a concomitant potential supply of residue biomass to be utilized for bioenergy generation. To facilitate the assessment of carbon f low through harvested wood products and the estimation of residue biomass potentially available for harvesting in these plantations, Wang et al. ( 2017) developed systems of additive and allocative aboveground biomass equations for individual trees using data from 239 trees that were destructively sampled and completely weighed in rotation age stands under three thinning regimes: unthinned (T0), once thinned (T1) and twice thinned (T2), referred to as stand types in plantation management. The additive equations predicted the total tree biomass in two major additive components, i.e., commercial log products and residue, in both fresh and dry weight.The allocative equations divided the product biomass into two sub-components, i.e., sawlogs and pulpwood, and separated the residue biomass into three sub-components: stump(including wood and bark biomass from ground level to stump height), branch and treetop, short of f-cut and waste sections due to stem deformity, defects, damage and breakage. These systems of equations for individual trees provide a sound basis for estimating total aboveground stand biomass in commercial logs and residues to complement the existing volume-based stand-level yield information that are most commonly reported and used in resource planning and decision support systems for forest management. When diameter and height measurements of individual trees are available from pre-harvest inventories, aboveground stand biomass in commercial logs and residues can potentially be obtained by scaling up estimates for individual trees, similar to the approach often adopted in forest biomass estimation(Snowdon 1992; Parresol 1999; Liu 2009; Vargas-Larreta et al. 2017). This potential can only be fully realised if three additional calculations are made in the scaling up process.First, dead standing, broken or badly damaged trees need to be included in the calculation of residue biomass. However, such trees are not routinely captured during pre-harvest inventory as they do not produce any commercial logs and so are most likely to be pushed over or cut and discarded as waste during harvesting. Second, not every tree produces both sawlogs and pulpwood; a small proportion of trees may only yield sawlogs but not any pulp wood (Wang et al.2017). Therefore, individual trees need to be allocated into two groups according to a predetermined empirical probability before the estimation of their sawlog and pulpwood biomass. Third, as is often the case in operational inventory,total tree height, a predictor variable in the systems of equations of Wang et al. ( 2017), is measured only for a certain number of selected trees but not for all individual trees in a plot. For the majority of trees, total tree height has to be estimated f irst before their biomass can be calculated using the systems of biomass equations.

Even with these additional calculations, scaling up biomass estimates of individual trees over a management area beyond the scale of inventory or sample plots may still face dif ficulties as individual tree data are usually not available at a larger scale. In present-day Australian softwood resource planning systems, stand level attributes such as stand height,density, basal area and volumes of log products that are extracted from plot-based inventory data are extrapolated or imputed spatially over a particular management area or at a broad estate level (Rombouts et al. 2015; Caccamo et al. 2018). In addition, growth and yield estimates forP.radiataplantations are often based upon models that predict stand-level attributes for any given stand type and age (Ferguson and Leech 1978; García 1984; Horne and Robinson 1988; Candy 1989; Whyte and Woollons 1990; Kimberley et al. 2005; Castedo-Dorado et al. 2007). Therefore, a more direct and ef ficient approach would be to link stand-level attributes derived from inventory plots, resource planning systems and outputs from conventional growth and yield models to biomass estimation of commercial logs and residues at the same spatial scale. Such an approach was suggested by LeMay and Kurz ( 2008) for estimating biomass,carbon stocks and stock changes in forests. To serve as an essential linkage of this kind, stand level biomass equations have been developed and adopted for plantations as well as natural forests (Bi et al. 2010; Castedo-Dorado et al. 2012;Paré et al. 2013; Jagodziński et al. 2019; Dong et al. 2019).These equations predict total aboveground stand biomass in terms of the structural components such as stemwood, bark,branches and foliage of all trees in a stand. To ensure the logical consistency of biomass additivity and the statistical ef ficiency in parameter estimation at the same time, stand biomass equations have increasingly been specif ied as a system of additive equations with cross-equational parameter constraints and estimated by taking into account the inherent error correlation among the system equations for the biomass components (Bi et al. 2010; Castedo-Dorado et al.2012; Jagodziński et al. 2019; Dong et al. 2019). However,stand-level systems of biomass equations for commercial logs and harvest residuals have so far not been developed for rotation age stands ofP. radiataor any other species.Building upon and extending the work of Wang et al. ( 2017)on individual trees, this paper aims to develop additive systems of stand biomass equations for predicting the fresh and dry weights of commercial logs and harvest residues and the weights of their respective sub-components in rotation ageP. radiatastands under three thinning regimes in NSW,Australia.

Material and methods

Study area and source of data

The Bathurst management area of the Northern Softwood Region, Forestry Corporation of NSW (FCNSW) encompasses 18 disjunct State Forest Plantations ofP. radiata,totalling 70,000 hectares spread across an east–west distance of about 130 km and a north–south distance of about 190 km on the central west slopes of NSW, Australia. The geographical location, geology, climatic and site conditions,history of plantation establishment of the management area and the initial planting density, three thinning regimes, and the rotation length of these plantations were described in detail by Knott and Ryan ( 1990) and by Wang et al. ( 2017) in an open access publication. As the second part of the same project on product and residue biomass carried out in the management area, this study used the same data set of plot measurements as described by Wang et al. ( 2017), which contained diameter at breast height overbark (DBHOB at 1.3 m above ground level as def ined in Australia) and total tree height (H) measurements of individual trees from 60 circular plots established across 12 selected compartments(i.e. sampling sites) in the management area. According to the current Australian soil classif ication, the soils of these sites included Ferrosols, Kurosoils and Dermosols with either clay loam, sandy loam or sandy clay loam texture on a variety of parent materials, including dacitic tuf fs, mudstone, shale, siltstone, and volcanic diorite (Dr. J. Turner,pers. comm.). Half of the 60 plots were in unthinned (T0)stands and the other half were evenly split between T1 and T2 stands. All T0 plots had a radius of 15 m. The T1 plots had a radius of 20 m, except for four which had a radius of 25 m. All T2 plots had a 25 m radius but one with a radius of 20 m. The increase in plot size from T0 to T2 stands was intended to take in at least 30 trees in every plot, which was considered the minimum number of trees required to provide reliable estimates of stand attributes for predicting aboveground stand biomass (c.f. Garcia 1998, 2006, Zhou et al. 2019) and to produce a full range of sawlog and pulpwood products for an adequate representation of product and residue biomass. The stand age of these plots ranged from 28 to 42 years, stand density from 163 to 1188 trees/ha, stand basal area from 30.5 to 89.2 m 2 /ha, and dominant height, calculated as the average height of the 100 largest diameter trees/ha, ranged from 26.6 to 38.5 m. The key stand attributes of these 60 plots were summarized and tabulated for each stand type in Wang et al. ( 2017). Besides the 60 plots, this study included one additional plot in an unthinned stand that was established and measured in the same way as part of the same project. However, the sampling site was later abandoned because a deep gully cutting through the compartment created spatial constraints for the placement of all 5 sample plots as intended for each site at a distance from each other that was practically operable for destructive sampling. Therefore, there were a total of 61 plots used in this study. The addition of this single plot to the data set did not alter the ranges of the key stand attributes previously tabulated in Wang et al. ( 2017), therefore the descriptive statistics of the stand attributes are not presented again here.

Stand biomass calculation

Across the 61 plots, we measured 3298 trees, including both live and standing dead trees, and trees with a broken stem or top or with other damages or anomalies. The DBHOB of these trees and broken stems varied between 6.2 and 71.6 cm and their total tree height (H) ranged from 1.5 to 43.0 m(Fig. 1). Obviously not all trees could produce a sawlog or even pulpwood. Firstly, the minimum small end diameter overbark (SEDOB) was 15 cm for small sawlogs and 8 cm for pulpwood and the minimum log length was 3.6 m according to log specif ications for the management area. Small trees not reaching the commercial size could only be cut to waste during harvesting and accounted for as part of residue in biomass calculations. Slightly larger trees that just became commercial in size could be harvested for pulpwood only but not sawlogs. Some larger live trees of full commercial size with a broken top or upper stem could be salvaged to produce either pulpwood or sawlogs or both. Secondly, standing dead trees and some live trees with severe stem damage beyond salvage could only be treated together with the small trees as part of the harvest residue in a plot. Therefore, the trees had to be screened and sorted into two broad groups,commercial and non-commercial, and subgroups within each broad group before calculating their product and residue biomass and that of the constituent components.

Tree assortment

An extensive exploratory analysis was carried out with the aid of statistical graphics to screen the data in several steps for further assortment. In the f irst step, standing dead trees with either a broken stem or not were identif ied by the binary mortality column and by reading the descriptive f ield notes of individual trees stored as character strings in the data f ile.At the same time, a small number of 24 live trees with eithera broken top or stem were also tagged. In the second step,the scatter plot of H against DBHOB for the remaining live trees that did not have any descriptive note f lagging stem brokage or damage were inspected to detect further outliers or anomalies. To facilitate this process, two nonlinear conditional quantile curves in the form of the three parameter Chapman-Richards function as specif ied below were drawn through the data cloud:

Fig. 1 (Left) Caterpillar plots of tree size for the 61 plots,where T1 plots are within the light blue strip, while T2 and T0 plots are above and below the blue stripe. Each horizontal line shows the median (red dot) together with the complete range of DBHOB or total tree height of all individual trees, i.e.either alive or dead, in a plot.(Right) Scatter plot of total tree height against DBHOB of all trees in each of the three stand types, where the dead trees and broken stems are shown by the grey circles. The upper and lower curves in each panel show the 0.50th and 0.005th nonlinear conditional quantiles of total tree height for any given value of DBHOB for all live trees across the 61 plots. The parameters for the two curves are , and as printed in the panel for T1 plots (see text)

whereHτ,aτ,bτandcτare total tree height in m and the three parameters corresponding to the chosen quantile τ of 0.5 and 0.005, andDrepresents DBHOB in cm (Fig. 1). This equation form was among the most commonly used model forms for tree height and diameter (H − D) models (see Huang et al.1992, 1999; Bi et al. 2000; 2012). For each value of, the three parameters in Eq. ( 1) were estimated by using the R package for quantile regression, quantreg (Koenker 2017,2018). The f irst quantile curve at τ = 0.5 showed the median of H for any given DBHOB and so represented the central trend of the height and diameter relationship. It was used to estimate the value of H for a small number of trees with a broken stem as described later. The second quantile curve at τ=0.005 delineated the lower limit of H for any given DBHOB. A small number of 12 live trees falling below this curve were deemed broken (Fig. 1). Although not evidenced by any descriptive f ield note, the abnormality was possibly overlooked during f ield measurements. In the third step, for every live tree with a broken stem, the height that the tree would reach if the stem were not broken was estimated from its DBHOB using the 0.50th nonlinear conditional quantile curve in the same form of Eq. ( 1) but f itted specif ically to the H and DBHOB data of other trees in the same plot. A broken stem that had a height greater than 50% of the estimated total tree height was regarded as salvageable and sorted into the commercial group. Otherwise, it was regarded as waste and put into the non-commercial group. In the f inal step,the stem prof iles of individual trees were predicted using the three overbark taper equations developed by Wang et al.( 2017) for trees in T0, T1 and T2 stands respectively in the form of the trigonometric variable-form taper equation of Bi ( 2000). Then the stem prof iles were evaluated against the SEDOB and log length specif ications of the smallest piece of commercially acceptable pulpwood in a simulated log cutting as demonstrated by Lu et al. ( 2018) and Shan et al. ( 2021). Trees too small to produce any pulpwood were regarded as non-commercial and sorted accordingly.

The commercial group had 2878 trees, including 1592 trees from the 31 unthinned (T0) plots, 668 trees from the 15 T1 plots and 618 trees from the 15 T2 plots, and accounted for about 87.3% of the total number of trees across the 61 plots. Among these commercial trees, there were 182 small ones that could only be harvested for pulpwood and 90% of them were in the T0 plots. The remaining 2696 trees in this group were found to be large enough to produce both sawlogs and pulpwood when their predicted stem prof iles were evaluated against the commercial log specif ications in log cutting simulations as described above. For any tree with a broken stem, a complete stem prof ile was derived f irst using its DBHOB and estimated tree height as predictors. Then a partial log cutting simulation was performed on the remaining part of the stem prof ile. The non-commercial group had a total of 420 trees, including 44 small non-commercial trees,12 live trees with broken stems that were too short for any wood product, with the rest being standing dead trees either with or without a broken stem. Most of these trees were in the unthinned (T0) plots (Fig. 1), most likely as a result of self-thinning and/or natural mortality in the even-agedP.radiatastands similar to the self-thinning stands described by Bi ( 2001).

Biomass calculations for individual trees

For individual trees in the commercial group, one system of additive equations and two systems of allocative equations,i.e., model (10), (12) and (13) in Wang et al. ( 2017), were used to estimate their product and residue biomass. The system of additive equations was used for predicting the product and residue biomass and the total above ground biomass of individual trees from their DBHOB, H and two dummy variables indicating stand types. The f irst system of allocative equations was used to allocate the estimated product biomass of each tree into sawlogs and pulpwood components.The second was employed to allocate the estimated residue biomass to stump, branch and waste components. The waste component included stem tops and short of f-cut sections due to stem anomalies and breakage during tree felling. Unlike the system of additive equations which has three predictor variables, the allocative equations rely on DBHOB only as the single predictor. For each of the three systems of equations, Wang et al. ( 2017) provided two sets of parameters for predicting fresh and dry weight respectively. In line with their work, both fresh and dry weight were obtained in our calculations of total tree and component biomass.

However, not all trees could produce both sawlogs and pulpwood in a harvesting operation. Some large trees would only produce sawlogs. Because the bucking pattern was optimised towards maximum value recovery, the remaining upper stem after sawlog cutting could no longer satisfy the SEDOB and length specif ications of even a small pulpwood log. On the other hand, small trees not reaching sawlog size could only produce pulpwood. As described in Wang et al. ( 2017), out of the 239 trees that were destructively sampled following stratif ied random sampling for developing the biomass equations, there were 36 trees that produced sawlogs only but not any pulpwood,representing about 15% of all sample trees. An extensive exploratory analysis showed that the occurrence of these trees could only be regarded as at random because it did not relate to or associate with any tree and stand attributes including DBHOB, total tree height, stand type and particular plots or sites. To mimic this pattern of log production in a rotation-age clearfell harvest, a binary random number was generated from a binomial distribution with ap-value of 0.15 for each tree. For trees with a random binary number of 1, all their product biomass was allocated to the sawlog component, none to pulpwood. For the 182 small trees that were identif ied to produce pulpwood only during tree assortment, their product biomass was allocated accordingly. For several live trees with a broken stem taller than 50% of their estimated total tree height,their product, stump and waste biomass was estimated but branch biomass was ignored. The estimation followed an ad hoc procedure that involved the combined use of the following biometric functions: (1) a plot-specif ic nonlinear H–D quantile curve, (2) a stand-type-specif ic taper equation as described previously, (3) the total stem (i.e.,both stemwood and bark) biomass equation of Baker et al.( 1984) forP. radiata, and (4) the allocative systems of biomass equations of Wang et al. ( 2017). For the sake of brevity, the procedure was not described in detail in this paper.

As there were four categories of trees in the non-commercial group, their biomass calculation varied accordingly.For small live trees with an unbroken stem, the total aboveground tree biomass was treated as residue biomass and allocated to the stump, branch and waste components using both the additive and allocative equations of Wang et al. ( 2017).For live trees with a broken stem that was shorter than 50%of their estimated total tree height, the ad hoc procedure described above was followed, but the calculated stem biomass was allocated only to the stump and waste components.For standing dead trees with an unbroken stem, the stem dry weight was calculated using the total stem biomass equation of Baker et al. ( 1984) and allocated to stump and waste components. For standing dead trees with a broken stem, the dry weight of the stem was estimated through the ad hoc procedure described above. For the live trees in both the commercial and the non-commercial groups, biomass was calculated in both fresh and dry weight. The total stem moisture content of standing dead trees would naturally be lower than that of live trees as observed for other species (Bi et al. 2015).The dead stems were neither completely fresh as live stems nor as dry as oven-dried biomass samples. As dead stems were not sampled for moisture content, their average fresh weight to dry weight ratio remained unknown. However,to obtain at least some estimate of the fresh weight for the biomass components of dead trees, the dry weight of each biomass component was multiplied by a factor calculated as the average ratio of the fresh weight to dry weight of the product part of the commercial trees.

Scaling up individual tree biomass to stand-level

The calculated fresh and dry weights of product and residue biomass and those of their respective components of all standing individual trees, either dead or alive, within a plot were summed component by component and divided by the plot area to obtain the stand level estimates of component as well as total aboveground stand biomass in tons per hectare. At the same time, stand attributes of live trees in the plot were calculated, which included stand age, density, basal area and stand height, taken as the mean height of 100 largest diameter trees/ha on a pro rata basis. The scaled-up biomass of all major and sub-components of the 61 plots were examined in relation to the four stand attributes through interactive scatter plot matrix to assess their inter-variable dependence or correlation structures (Fig. 2).For each component, the relationship between the scaledup fresh and dry weight was examined in preparation for model building (Fig. 3). In addition, the percentage allocations of total aboveground stand biomass in both fresh and dry weight to the two major components as well as to the f ive sub-components were derived for each plot. The patterns of biomass allocation were then summarized across the three stand types to gain a better understanding of the data to be modelled (Fig. 4).

Specif ications of two- and single-stage systems of equations

Two approaches to model specif ication were compared for predicting the scaled-up stand level component and total biomass in both dry weight and fresh weight. The f irst was the two-stage approach of Wang et al. ( 2017), which combined one system of additive equations for product, residual and total aboveground biomass at the f irst stage with two systems of allocative equations at the second stage to allocate the predicted product and residue biomass from the f irst stage to their respective components. The f irst-stage system of additive equations incorporated all stand variables as predictors:

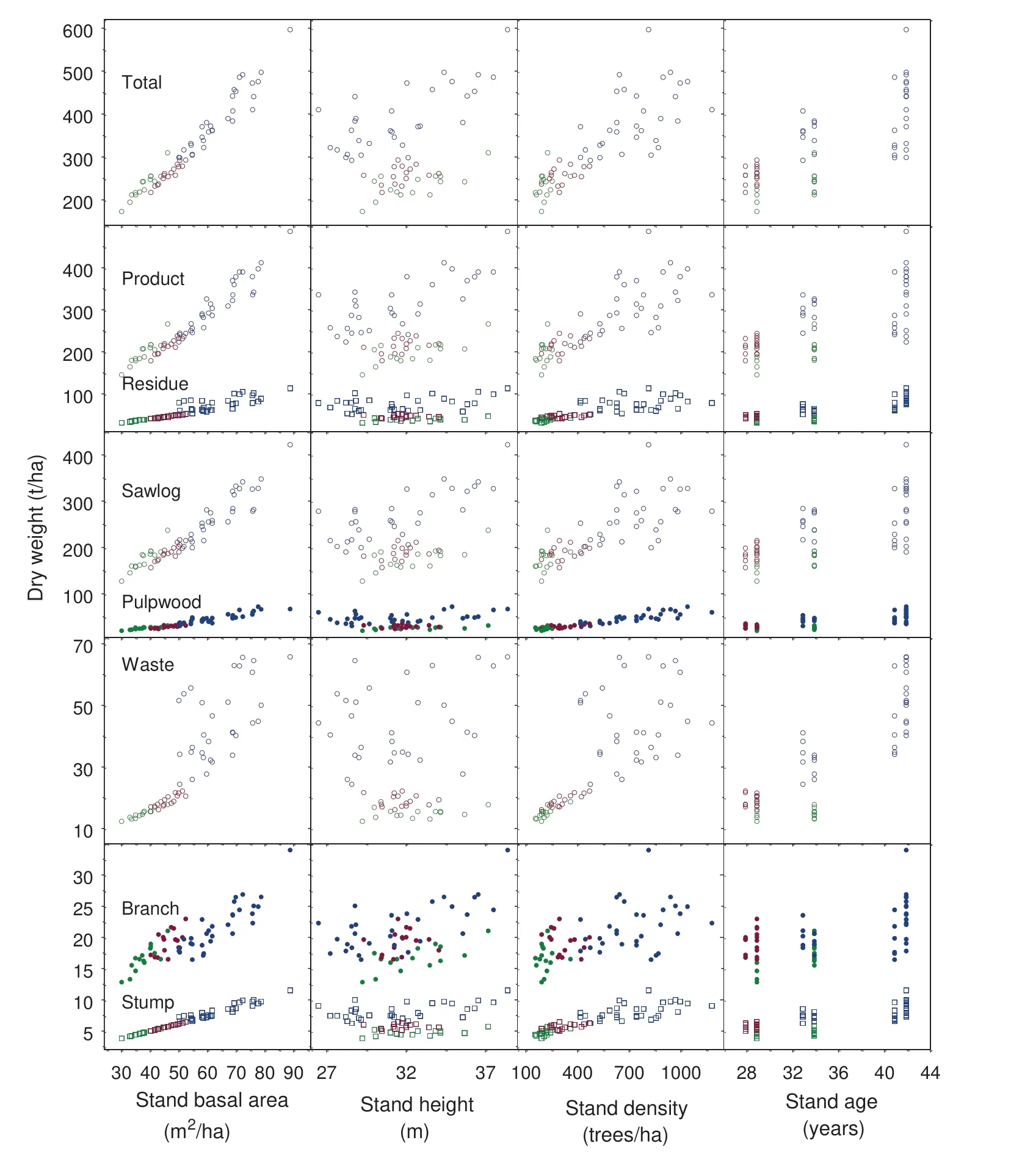
Fig. 2 Scatter plots of scaled-up component and total aboveground stand biomass in dry weight against four stand variables for T0 (blue), T1 (red)and T2 (green) stands

Fig. 3 Multi-panel display of fresh and dry weight relationships for component and total aboveground stand biomass of the 61 plots in T0, T1 and T2 stands (blue, red and green circles). In each panel, the line through the data points indicates the average fresh to dry weight ratio for all stand types. The line of unity was plotted below the average ratio line to serve as a reference

Fig. 4 Boxplots summarizing the percentage allocations of total aboveground stand biomass in both fresh and dry weight to the two major and f ive sub-components across the three stand types

whereYsawandYpulpstand for sawlog and pulpwood biomass in either fresh or dry weight in t/ha,is the corresponding predicted product biomass from the f irst stage system of additive equations,rijare coef ficients,11and12are the error terms. Another was for allocating residue biomass to three components:

where T0 and T2 are dummy variables, equal to 1 for the stand type they represent and 0 otherwise, anddijare their coef ficients. The incorporation of the two dummy variables in the exponent of G gave the best predictive performance among alternatives that were carefully compared during model specif ication, although the details were not given here for the sake of parsimony. Similar approaches of incorporating dummy variables in a single or a system of biomass equations can be found in Zeng et al. ( 2011); Fu et al. ( 2012,2014) and Wang et al. ( 2017). The predicted product and residue biomass,proandres, for dif ferent stand types would be allocated to their respective subcomponents through the same systems of allocative equations as specif ied in Eqs. ( 3)and ( 4). Incorporating dummy variables for stand types into the systems of allocative equations created a higher level of complexity in both model specif ication and estimation but led to little gain in predictive performance.

Unlike the two-stage model specif ications in the f irst approach, a single system of additive equations was specif ied for all f ive biomass components in the second approach:

where all variables, coef ficients, error terms and their properties are as previously described. Unlike the two-stage systems of Eqs. ( 2 and 5), the two single stage systems of Eqs. ( 6 and 7) did not include component equations for product and residue biomass.

Parameter estimation

As often observed in both individual tree and stand level biomass data, heteroscedasticity existed in the scale-up data for all the component and the total aboveground stand biomass, although to dif ferent degrees (Fig. 2). To negate the ef fects of heteroscedasticity on the second order properties of parameter estimates, all systems of additive and allocative equations were estimated using the generalised method of moments (GMM) in the PROC MODEL procedure of SAS/ETS. Under heteroscedastic conditions, the GMM estimator produces ef ficient parameter estimates without any specif ication of the nature of the heteroscedasticity (Greene 1999).It has been used to estimate systems of additive as well as allocative biomass equations (Bi et al. 2004, 2010, 2015;Wang et al. 2017). In addition to the GMM, the systems of equations were also f itted to the data using weighted nonlinear seemingly unrelated regressions (WNSUR) as demonstrated by Parresol ( 2001). Consistent with the f indings of Wang et al. ( 2017) when estimating systems of biomass equations for individual trees, the mean squared errors for the system equations indicated that GMM was equivalent or slightly better than WNSUR. Therefore, parameter estimates obtained using WNSUR are not reported here.

Although developed within the framework of nonlinear error-in-variable models, the system of allocative equations can be regarded as a system of simultaneous equations when the number of equations is equal to the number of variables with errors in the system (Tang et al. 2000, 2001, 2008). In such cases, the system of allocative equations can also be estimated by WNSUR and GMM using the PROC MODEL Procedure of SAS/ETS without resorting to the specialist software ForStat 2.2 developed by the Chinese Academy of Forestry and documented in detail by Tang et al. ( 2008). As exemplif ied by Dong et al. ( 2015) and Wang et al. ( 2017),the SAS procedure and ForStat produced almost identical parameter estimates and validation statistics.

The three dependent variables,Ypro,YresandYtotin Eq. ( 2)represented either fresh or dry weight, so the system of three equations was estimated twice to obtain two separate sets of parameter estimates initially for fresh and dry weight,respectively. The initial values for the parameters of each system equation were obtained through linear least squares regression after transforming the equation into a log linear form. The Marquardt method was specif ied in the procedure to minimize the objective function since this method is essentially an improved Gauss–Newton method by incorporating the steepest descent method into the iterative update scheme (Marquardt 1963; Draper and Smith 1998). This method has been found most useful for parameter estimation of nonlinear growth models in forestry, particularly when parameter estimates are highly correlated (Fang and Bailey 1998; Fekedulegn et al. 1999; Bi et al. 2012). As there was a close linear relationship between the fresh and dry weight of each biomass component (Fig. 3), the residual errors of the fresh and dry systems of equations were highly correlated. However, the separate estimations did not take such correlations into account. To overcome this def iciency and further gain statistical ef ficiency in parameter estimation, the two systems of equations for fresh and dry biomass were jointly estimated as one system of six equations within the same the PROC MODEL Procedure. In the same way,the fresh and dry systems of additive equations specif ied in Eq. ( 5) were jointly estimated and so were those specif ied in Eq. ( 6). However, the systems of equations specif ied in Eq. ( 7) were still estimated separately for fresh and dry weight because convergence could not be reached for joint estimation. Following parameter estimation, a generalizedR 2was calculated for each system equation in the form of the model ef ficiency coef ficient originally proposed by Nash and Sutclif fe ( 1970):

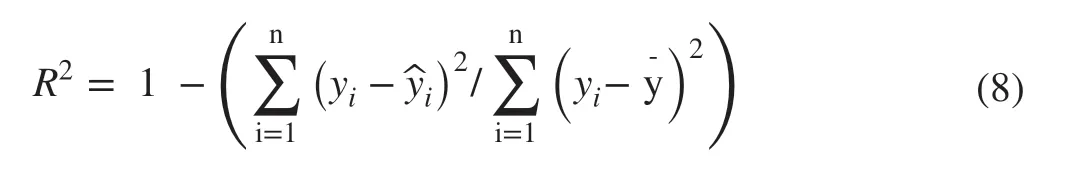
Evaluation and comparison of prediction accuracy

Benchmarking statistics

The predictive performances of the two- and single-stage systems of biomass equations were evaluated and compared through a leave-one-plot-out cross validation procedure that was carried out for both fresh and dry weight of all biomass components. All previously specif ied systems of additive and allocative equations were repeatedly f itted 61 times.Each time, biomass data from one of the 61 plots were left out from the f itting process. From the systems of equations estimated using data from the remaining 60 plots, the predicted values of total aboveground stand biomass, all major and sub-component biomass were obtained for the left-out plot that was independent of the f itting process. For each of these predicted values of theith left-out plot () , a prediction error () was calculated as the dif ference between the observed (yi) and predicted biomass, i.e.=yi−, in t/ha.For the two single-stage systems of equations (Eqns. 6, 7),the predicted value of product and residue biomass were taken as the sum of their respective predicted components.Following the repeated f itting, six benchmarking statistics were calculated for the predictions of all component and total aboveground stand biomass in fresh and dry weight for the 61 plots. These benchmarking statistics included the mean error of prediction (MEP), the mean percentage error of prediction (MPEP), the mean absolute error of prediction(MAEP), the mean percentage absolute error of prediction(MPAEP), the mean squared error of prediction (MSEP) and the prediction coef ficient of determination () and were calculated:

In addition to the benchmarking statistics, the predicted biomass of all major and sub-components in each plot was divided by the predicted total aboveground stand biomass and converted to percentage allocations for the plot. The model-derived allocations were compared with the observed percentage allocations of total aboveground stand biomass to the major and sub-components as summarised in Fig. 4 through simple scatter plots to further assist model evaluation and comparison of prediction accuracy.

Prediction error variance and approximate conf idence bands

In addition to the benchmarking statistics, a prediction error variance function was derived for each system equation in order to delineate an approximate conf idence band containing about 90% of the observed data about the mean curve of predicted biomass from the equation. Similar to the close match between PRESS and ordinary residuals that is often observed in linear regression analysis without the presence of outliers (Allen 1974; Myers 1990), the prediction errors () from the leave-one-plot-out cross validation procedure had an almost total correlation along the identical(45 degree) line with their corresponding residuals obtained when all data were used for parameter estimation. Pearson’s correlation coef ficient between PRESS and ordinary residuals was at least 0.99 or greater for every biomass component for all systems of equations. Therefore, the widely applied methods of modelling residual heteroscedasticity as shown for example in Parresol ( 2001), Bi et al. ( 2004, 2010, 2015)and Wang et al. ( 2017) were followed for modelling prediction error variance in this study. For each system equation,the prediction error variance,Var() , was assumed to be a power function of the estimated mean ( Y):

AsVar() was an unknown quantity, the squares of prediction errors (2) were used as representatives of their variances:

Equation ( 15) was linearized by taking logarithmic transformation of both sides and estimated through least squares regression for system equations that did not incorporate dummy variables. For systems of equations with dummy variables, a single dummy variable was incorporated in the intercept term to separate the thinned and unthinned stands:

where ln indicates natural logarithm,Iis a dummy variable which equals 0 for unthinned stands and 1 for thinned stands of both T1 and T2 types, d and b are parameters.This prediction error variance function was adopted after a comparison with the alternative function with two dummy variables. Adding an extra dummy variable did not make the skedastic patterns of prediction error more discernible for all system equations.

As the prediction error variance function was estimated using log transformed data, it had an inherent bias when back transformed from logarithm. The existence of such bias has been well-recognised in biomass estimation as well as in applied statistics (Baskerville 1972; Beauchamp and Olson 1973; Wiant and Harner 1979; Flewelling and Pienaar 1981;Sprugel 1983; Snowdon 1991; Shen and Zhu 2008; Zeng and Tang 2011). To reduce such bias, Snowdon’s ( 1991) bias correction factor (s) was calculated for the residual variance function of each system equation. The more complex functional methods proposed by Shen and Zhu ( 2008) were also attempted, but they brought little gain over Snowdon’s much simpler factor. Following the steps outlined in Bi et al.( 2015) and Wang et al. ( 2017), the estimated variance function,Var(), was multiplied bysf irst, then the square root of the product was used to weigh the prediction errors. The 5th and 95th percentiles from the distribution of weighted residuals were taken as the approximate lower and upper conf idence limits of prediction error at the 90% level. For any predicted value of biomass, Y, the approximate 90%conf idence band of the observed data were delineated by

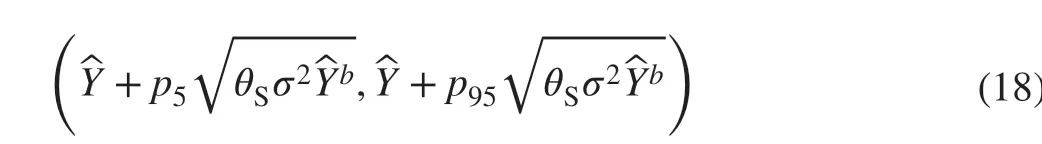
wherep5andp95are the 5th and 95th percentiles of the distribution of weighted errors of prediction. Conf idence intervals thus obtained were not necessarily symmetric about zero since the distribution of weighted errors of prediction can be skewed.

Results

Two-stage systems of equations for general application

There were similarities as well as dif ferences between the two sets of parameters for the f irst stage system of additive Eqs. ( 2) that were jointly estimated for predicting the fresh and dry weight of product, residue and total stand biomass.In the component equation for product biomass, the parameter associated with stand basal area,12, was estimated to be 0.90 and 0.84 respectively for fresh and dry weight predictions (Table 1). The estimated13, the parameter associated with stand height, was 0.81 and 0.78 for the same two types of predictions. For neither parameter was the dif ference between the estimates for fresh and dry weight predictions signif icant at α = 0.05 according to the t-statistics that could be easily derived from the standard errors of the parameter estimates. In comparison, the remaining three parameters,10,11, and14, each had two signif icantly dif ferent estimates for predicting the fresh and dry weight of product biomass. In the case of14, the estimated value was -0.05 for fresh and 0.05 for dry weight predictions.

In the component equation for residual biomass, the parameter associated with stand basal area,22, was estimated to be 2.01 and 1.71 for fresh and dry weight predictions (Table 1). The parameter associated with stand height,23, was − 0.73 and − 0.62 for the same two types of predictions. The dif ference between the two estimates for fresh and dry weight predictions was marginally signif icant for22and not signif icant for23. The other three parameters,20,21and24, each had signif icantly dif ferent values for predicting fresh and dry weight biomass. The joint estimation of the two systems of additive equations for predicting the fresh and dry weight of product, residue and total stand biomass resulted in smaller standard errors for the estimated parameters as compared with the initial separate estimations.The percentage reductions in the standard error of parameter estimates in the component equation for product biomass ranged between 4.9% and 14.9% among the fresh weight parameters and between 8.6% and 21.6% for the dry weight parameters. In the component equation for residue biomass,the reductions ranged between 5.1% and 11.9% for the fresh weight parameters and between 8.4% and 21.8% for the dry weight parameters.The two sets of parameter estimates for the f irst secondstage Eq. ( 3) that allocated the predicted product biomass to sawlog and pulpwood in fresh and dry weight respectively were similar (Table 2). In contrast, signif icant dif ferences were detected by t-tests between the two sets of parameter estimates for the other second-stage Eq. ( 4) that allocated the predicted residue biomass into stump, branch and waste components in fresh and dry weight. The value ofR2was the highest for the sawlog allocation and the lowest for the branch allocation in both fresh and dry weight.

Table 1 Two sets of parameter estimates and their standard errors (SE) for the system of additive equations without dummy variables for stand types (Eq. 2). The two sets of parameters were estimated jointedly for predicting respectively the fresh and dry weight of product ( ̂Ypro) ,residue ( ̂Yres) and total stand biomass ( ̂Ytot) . PR(%) stands for percentage reductions in standard error of parameter estimates resulted from the joint estimation as compared to the separate estimation of the two systems of equations

Table 2 Parameter estimates and their standard errors (SE)for the two systems of allocative Eqs. ( 3) and ( 4) that allocate the predicted product and residue biomass from Eq. ( 2) into their respective components in fresh and dry weight

Two-stage systems of equations for specif ic stand types

With the incorporation of dummy variables for stand types in the f irst-stage system of additive Eq. ( 5), the parameter associated with stand age,11, in the component equation for product biomass had two similar estimates for fresh and dry weight predictions (Table 3). The two estimates of12, the parameter associated with stand basal area, were both in the close neighbourhood of 1;that of13, the parameter associated with stand height,also had similar values for fresh and dry weight predictions. In the component equation for residue biomass, the three parameters,21,22and23, each had two estimated values that were not signif icantly dif ferent for fresh and dry weight predictions, but the other two parameters,20and24, showed otherwise. The joint estimation of the two systems of additive equations for fresh and dry weight predictions also led to smaller standard errors for the estimated parameters as compared with the initial separate estimations. The percentage reductions in standard errors for parameter estimates in the component equation for product biomass ranged between 4.4% and 18.7% for fresh weight parameters and between 10.1% and 22.8% for dry weight parameters. In the component equation for residuebiomass, the reductions ranged between 3.9% and 15.7%for fresh weight parameters and from 9.9% to 24.2% for dry weight parameters (Table 3). Now Yproand Yresfrom the f irst-stage systems of additive Eq. ( 5) with dummy variables were taken as the predictor variables in the two second-stage systems of allocative Eqs. ( 3 and 4). The new parameter estimates shown in Table 4 were similar to their counterparts in Table 2 with only slight, nonsignif icant dif ferences, but their standard errors tended to be smaller.

Table 3 Two sets of parameter estimates and their standard errors (SE) for the system of additive equations with dummy variables for stand types (Eq. 5).The two sets of parameters were estimated jointly for predicting respectively the fresh and dry weight of product ( ̂Ypro) ,residue ( ̂Yres) and total stand biomass ( ̂Ytot) . PR(%) stands for percentage reductions in standard error of parameter estimates resulted from the joint estimation as compared to two separate estimations of the system of equations

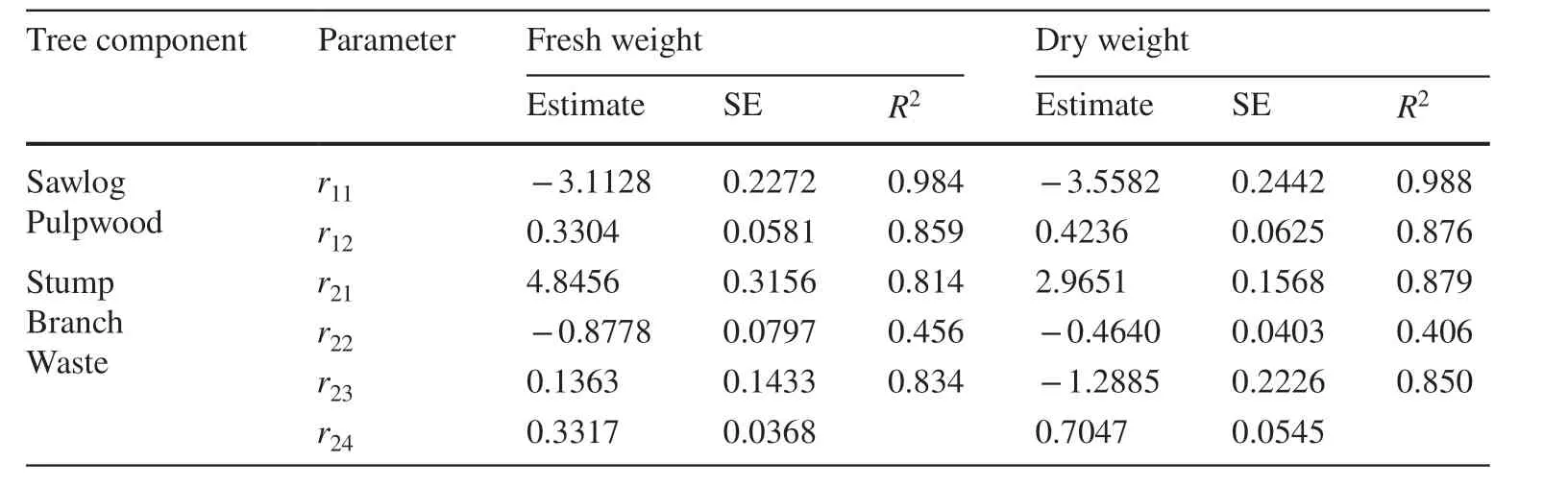
Table 4 Parameter estimates and their standard errors (SE)for the two systems of allocative Eqs. ( 3) and ( 4) that divide the predicted product and residue biomass from Eq. ( 5) into their respective components in fresh and dry weight

Single-stage systems of additive equations for general application

The joint estimation of the two single-stage systems of additive Eq. ( 6) for respective fresh and dry weight predictions also resulted in appreciable reductions in the standard errors of all parameter estimates as compared with the initial separate estimations. The percentage reduction ranged from 2 to 34% for parameters in the fresh weight equations and from 3.8% to 35% for parameters in the dry weight equations. In the component equation for sawlog biomass, the estimated12, the parameter associated G was 0.98 for fresh weight and 0.92 for dry weight (Table 5). The estimated13, the parameter associated H, was 0.84 for fresh weight and 0.82 for dry weight. The estimated14, the parameter associated with N, was slightly less than zero for fresh weight, but about zero for dry weight. The values ofR2ranged between 0.75 and 0.97 for the fresh weight components and between 0.85 and 0.98 for the dry weight components. For total aboveground stand biomass in both fresh and dry weight,theR2value was greater than 0.99.

Single-stage systems of additive equations for specif ic stand types

The incorporation of dummy variables for stand types in the single-stage systems of additive Eqs. ( 7) improved the f it for all f ive component equations (Table 6). The values ofR2ranged between 0.85 and 0.99 for the fresh weight components and between 0.89 and 0.99 for the dry weight components. For total aboveground stand biomass in both fresh and dry weight,R2values were greater than 0.99 and closer to 1.In the component equation for sawlog biomass, the estimated12, the parameter associated G was 1.11 for fresh weight and 1.05 for dry weight, but the dif ference was only marginally signif icant. The estimated13, the parameter associated H, was 0.71 for fresh weight and 0.74 for dry weight. Here the dif ference was small and not signif icant. The estimated14, the parameter associated with N, was − 0.099 for fresh weight and − 0.075 for dry weight prediction. Both estimates were signif icantly less than zero and the dif ference between them was not signif icant. Although estimated separately for fresh and dry weight predictions because convergence could not be reached for joint estimation, the incorporation of dummy variables also gained some ef ficiency in the parameter estimates. The standard errors of parameter estimates for predictor variables as shown in Table 6, when evaluated relative to the values of the estimated parameters, were more or less comparable to that for the same predictors without the incorporation of the dummy variables for stand type as shown in Table 5.

Comparative prediction accuracy

Benchmarking statistics

Although without dummy variables for stand types, the general two-stage systems of equations predicted component and total stand biomass in fresh and dry weight with only small biases (Fig. 5). The MEP values were between − 0.07 and 0.43 t/ha for product, residue and total stand biomass and between − 0.30 to 0.55 t/ha for subcomponent biomass predictions. The corresponding MPEP values ranged from 0.08% to 0.48% for product, residue and total stand biomass and from − 1.22% to 2.54% for component biomass predictions. With the incorporation of dummy variables, the stand type-specif ic systems of equations had slightly smaller biases for predicting major component and total stand biomass, but a similar degree of bias to that of the general two-stage systems of equations for all sub-component biomass predictions (Fig. 5). The incorporation of dummy variables substantially increased the precision of prediction for the major component and total stand biomass as well as sawlog and waste biomassin both fresh and dry weight, for which the values of MSEP decreased by between 5 and 67%. Consequently,the model-derived biomass allocations were closer to and more consistent with the observed percentage allocations of total aboveground stand biomass to the major and subcomponents (Fig. 6). The allocations to product biomass in fresh weight were in the range of 73%–83% with an average of 78% for the unthinned (T0) stands, between 76 and 83% with a mean of 80% for the T1 stands, and within 80–86% with an average of 83% for the T2 stands. When biomass predictions were in dry weight, the derived allocations to product biomass slightly increased to 76%–84%with an average of 81% for the T0 stands, to 80%–85%with a mean of 83% for the T1stands and to 83%–87%with an average of 85% for the T2 stands. The biomass allocations to sawlogs were the highest for the T2 stands,averaging 72% and 75% in fresh and dry weight respectively, greater than the corresponding values of 69% and 72% for the T1 stands and 67% and 69% for the T0 stands.The thinned stands had slightly greater allocations to the branches but less allocations to the waste component than the unthinned stands (Fig. 6).

Table 5 Two sets of parameters and their standard errors (SE)for the single-stage system of additive equations (Eq. 6)that were jointly estimated for predicting respectively the fresh and dry weight of component and total aboveground stand biomass. PR (%) stands for percentage reductions in standard error of parameter estimates resulted from the joint estimation as compared to two separate estimations of the systems of equations

The benchmarking statistics from the leave-one-plot-out cross validation procedures also showed that the singlestage systems of additive equations performed generally better than the two-stage systems of additive and allocative equations (Fig. 5). When dummy variables for stand types were not incorporated as predictors in the models, the MSEP values for fresh weight predictions from the singlestage system of additive equations (Eq. 6) were 2.0% smallerfor total stand biomass, but 5.0% and 9.3% larger for product and residue biomass than that from the two-stage systems of equations (Eqs. 2, 3 and 4). The MSEP values for the sawlog and pulpwood components in the product category were 9.2% and 26.6% smaller, while that for the stump, branch and waste components in the residue category were respectively 10.6% larger but 72.6% and 12.9% smaller. For dry weight predictions, the MSEP values were 1.9%, 3.6%, and 9.3% larger for product, residual and total aboveground stand biomass, but were 10.6% and 48.3% smaller for the sawlog and pulpwood components and 82.2%, 96.7%, and 7.0%smaller for the stump, branch and waste components. With the incorporation of dummy variables for stand types in the model specif ications, the MSEP values for fresh weight predictions from the single-stage system of additive equations(Eq. 7) were 9.1% and 2.2% smaller for product and residue biomass, but 6.4% larger for total stand biomass than that from the two-stage systems of equations (Eqs. 5, 3 and 4).For the sawlog and pulpwood components, the MSEP values were 13.9% and 37.7% smaller, while for the stump, branch and waste components they were 10.4%, 93.6%, and 23.1%smaller, respectively. The MSEP values for dry weight predictions from the single-stage system of additive equations (Eq. 7) were 5.6% and 4.2% smaller for product and residue biomass, but 4.5% larger for total biomass. For the sawlog and pulpwood components, the MSEP values were 14.2% and 53.1% smaller. For the stump, branch and waste components, they were 84.8%, 97.1%, and 17.5% smaller respectively. For both single- and two-stage models, the incorporation of dummy variables for stand types led to substantial reductions of MSEP for most biomass components and total stand biomass in both fresh and dry weight (Fig. 5).

Table 6 Two sets of parameter estimates and their standard errors (SE) for the single-stage system of additive Eqs. ( 7)that were obtained by running two separate estimations for predicting respectively the fresh and dry weight of component and total aboveground stand biomass

Fig. 5 Dot plots displaying six benchmarking statistics of predictive performance in fresh and dry weight (upper and lower halves) as calculated in Eqs. ( 9– 14) for each system of equations. In each panel,statistics for predictions of product, residue and total aboveground stand biomass are shown from top down within the shaded strip,while that for predictions of sawlog, pulpwood, stump, branch and waste biomass are shown from top down in the unshaded area

The mean error of prediction (MEP) and mean percentage error of prediction (MPEP) for all component and total stand biomass in both fresh and dry weight were small and practically negligible for both single- and two-stage models,regardless of whether dummy variables were incorporated into the models. The mean percentage error of prediction(MPEP) was mostly within ± 0.5% for product, residue and total stand biomass across the four systems of equations (Fig. 4). The values of MPEP for sawlog biomass were within ± 0.18% and that for pulpwood biomass were mostly positive and less than 1.5%. For the three residue components, MPEP ranged narrowly between − 0.92% and 1.56%for the single-stage models (Eq. 6, 7) and slightly wider,from − 1.22% to 2.85%, for the two-stage models (Eqs. 2,3, 4 and 5).

Prediction error variance and approximate conf idence bands

For the sake of parsimony, prediction error variance functions and approximate conf idence bands are presented here for the two single-stage systems of additive equations (Eqs. 6 and 7) only as their predictive performances were better than those of the two-stage models. For the general single-stage system of additive equations (Eq. 6), the exponent (b) in the prediction error variance function was almost zero for product biomass in both fresh and dry weight (Table 7). In this case, the prediction error variance was almost a constant that was determined solely by the estimated scale factor2and consequently the width of the approximate 90% conf idence band derived from Eq. ( 18) changed little as the predicted values of biomass increased (Fig. 7). This pattern of prediction error variance ref lected to a large degree that for predictions of sawlog biomass, the major component of product biomass as shown in Fig. 4. The estimated values ofbwere much smaller than 1 for predictions of sawlog biomass in both fresh and dry weight, therefore the approximate conf idence bands for the predictions expanded little with the predicted biomass. In contrast, the estimates ofbwere greater than 3 for predictions of pulpwood biomass in both fresh and dry weight (Table 7) and so the approximate conf idence bands expanded with the predicted values (Fig. 7). Unlike the case for product biomass, the estimated values ofbwere not close to zero but greater than 2 for residue biomass predictions in fresh as well as dry weight, so the approximate conf idence band became much wider as the predicted residue biomass increased. This expanding pattern of prediction error variance for residue biomass ref lected the pattern for waste biomass to a large extent and, to a lesser degree,the patterns for the stump and branch components (Table 7,Fig. 7).

Fig. 6 Observed allocations of total aboveground biomass to the f ive biomass components plotted against the corresponding model-derived allocations with a diagonal line of unity for the 61 plots in T0 (blue),T1 (red) and T2 (green) stands. The two columns of graphs on the left are for the system of Eq. ( 2) that did not incorporate dummy variables for stand types, while the two columns on the right are for the system of Eq. ( 5) where dummy variables were specif ied for stand type-specif ic applications

For the stand type-specif ic single-stage system of additive equations (Eq. 7), the estimated scale factor in log form(T2) that was associated with the dummy variable for thinned stands (T1 and T2) in the prediction error variance function (Eq. 17) was negative or close to zero for all but the stump component in both fresh and dry weight (Table 8). As a result, the approximate conf idence bands for thinned stands were slightly narrower than those for unthinned stands for predictions of all component and total aboveground stand biomass in both fresh and dry weight, except for the stump component (Fig. 8). The patten of change in the approximate conf idence band with the predicted biomass of each component was similar to that shown in Fig. 7 for the general system of equations. So, the comparative dif ferences in the skedastic pattern of prediction error across the major and sub-components were comparable to those for the general system of equations.

Discussion

Biomass data are inherently hierarchical at both individual tree and stand levels, where the total is the sum of all major components and each major component is comprised of certain sub-components. To maintain this inherent logical consistency in a system of equations for predicting component and total biomass, two approaches have been generally adopted over the past 20 years. One is the bottom-up additive approach, which is well known and has been widely applied in the English literature (Parresol 1999, 2001; Bi et al. 2001,2004). The other is the top-down allocative approach, which was developed within the framework of error-in-variable models by Tang et al. ( 2000, 2001) and has been used mostly in China. Although the two approaches dif fer in model specif ication and also in the method of parameter estimation, their predictive performance is, by and large, comparable, being either equivalent or with one being slightly superior to the other (Dong et al. 2015; Fu et al. 2016). Even when the additive and allocative systems of nonlinear biomass equations were specif ied within a probabilistic framework and f itted using Gaussian maximum likelihood estimation, their predictive performances were hardly dif ferentiable (Af fleck and Diéguez-Aranda 2016). The results of this study showed that the single-stage systems of additive equations generally performed better than the two-stage systems of additive and allocative equations (Fig. 5). The improvements were substantial for the f ive sub-components and less so for the two major components but slightly reversed for total stand biomass when the MSEP values of the two approaches from the leave-one-plot-out cross-validation process were compared.As predicting the biomass of the major and sub-components of rotation-age stands inP. radiataplantations was the primary objective of this study, the two single-stage systems of additive equations (Eqs. 6 and 7) are recommended for use in forest management.

The two single-stage systems initially included component equations for product and residue biomass that were constrained to be the sum of their respective sub-components in the model specif ications. However, placing two additional additivity constraints led to a greater degree of complexity in the model structure, particularly in the stand type-specif ic system of equations (Eq. 7) with dummy variables. It made little dif ference to the f it statistics when all data were used in the f itting but caused some complications in parameter estimation during the leave-one-plot-out repeated f itting and validation procedure. Parresol ( 2001)brief ly illustrated the way to impose multilayered hierarchical additivity constraints upon major and sub-components in a system of additive biomass equations, but he did not explore further through model estimation and comparison.Few subsequent studies have done so but they did show that imposing additional constraints brought little or no gain and even a slight loss in prediction accuracy for the major components in some circumstances (Dong et al. 2015; Zhao et al.2015; Widagdo et al. 2020). Although placing multilayered hierarchical additivity constraints in a system of biomass equations can be appealing theoretically, its practical implications in model specif ication, parameter estimation and prediction accuracy of component and total biomass may need to be carefully evaluated in future studies.

The joint estimation of two sets of parameters of the same system of additive equations for both fresh and dry weight predictions led to much improved statistical ef ficiency in parameter estimation as compared with running two separate estimations. The reductions in the standard error of parameter estimates ranged from 2 to 35% among the parameters of the three systems of equations (Eqs. 2, 5 and 6) that were each estimated this way (Tables 1, 3 and 5). The gain instatistical ef ficiency varied even among parameters of the same system equation for one biomass component. For the two systems of equations that predicted product, residue and total aboveground biomass in the two-stage approach (Eqs. 2 and 5), the gain in statistical ef ficiency was greater for the dry weight parameters than for the fresh weight equations.Interestingly, the results were mixed for the system of additive equations that predicted all f ive sub-components (Eq. 6),where the gain was greater for dry weight parameters for sawlog, stump and waste biomass but vice versa for pulpwood and branch biomass. The overall gain in statistical ef ficiency of parameter estimation could only be attributed to the close correlation between the fresh and dry weight of each and every component as well as the total aboveground stand biomass (Fig. 3). Such an overall gain will not only facilitate variable selection in the model building process,particularly when developing systems of additive biomass equations that involve a number of predictor variables, but also sharpen statistical inferences about the parameters once they are estimated. The joint estimation of two sets of parameters of one system of additive biomass equations has not been reported in the literature. This approach was contemplated but not implemented in the studies of Bi et al.( 2015) and Wang et al. ( 2017). Because of the advantages from the improved statistical ef ficiency in parameter estimation, this approach is recommended for use in future studies that aim to simultaneously predict the fresh and dry weight of component and total biomass of either individual trees or forest stands through a system of equations.

Table 7 Estimated scale factors 2 in log form and exponents ( b) of the prediction error variance functions for the general system of additive equations without dummy variables for stand types (Eq. 6)

Table 7 Estimated scale factors 2 in log form and exponents ( b) of the prediction error variance functions for the general system of additive equations without dummy variables for stand types (Eq. 6)

θs is Snowdon’s bias correction factor, p5 and p95 are the f ifth and ninety-f ifth percentiles of the weighted prediction errors. Two sets of estimates are shown for fresh and dry weight predictions of component and total aboveground stand biomass

?

As a by-product of timber harvesting, the amount of residue biomass is determined to a large degree by log specif ications used in bucking as well as the harvesting methods and technology. The commercial product specif ications for plantations in the study area were based largely on the minimum small end diameter overbark (SEDOB), which was 26 cm for sawlogs of 2.5–3 m in length, 15 cm for small sawlogs of 3.6–6.1 m in length, and 8 cm for pulpwood.The log specif ications and prices were used by cut-to-length harvesters to optimize the bucking strategies for individual trees during harvesting without on-site debarking (see Lu et al. 2018; Shan et al. 2021). As the cut-to-length harvesting yields signif icantly higher levels of residue than the traditional whole-tree or tree-length harvesting (Ghaf fariyan et al. 2012, 2015; Ghaf fariyan and Apolit 2015), the systems of equations developed here are only applicable to plantations with similar log specif ications and harvesting methods. A case in point is the simple linear relationship between the potential harvest residue biomass in dry weight and stand basal area reported by Cartes-Rodríguez et al.( 2016) forP. radiataplantations in south-central Chile. They destructively sampled 250 trees from 27 stands with stand basal areas over a range similar to that of the 61 plots in this study. But f ive of their 27 stands had stand densities between 1200 and 1600, much higher than the unthinned plots in our study. The destructive sampling appeared to mimic a tree-length (from stump to a SEDOB of 8 cm) harvesting with on-site debarking and stembark was treated as part of harvest residue. Their biomass samples were dried at 65 °C,much lower than the drying temperature of 103 °C in our case as documented in Wang et al. ( 2017). Lower drying temperatures tend to result in less loss of not only volatile organic compounds but also water in biomass samples.Matthews ( 2010) found approximately 2.5% of additional moisture in pine samples dried at 65 °C compared to when samples were dried at 103 °C in an air-conditioned laboratory at 20 °C and 40% relative humidity. These dif ferences in the method of harvesting, in the composition of harvest residues, and in the drying temperature of biomass samples could lead to dif ferences in the predicted residue biomass.For the same stand basal area, the predicted harvest residue biomass in dry weight from the simple linear relationship of Cartes-Rodríguez et al. ( 2016) was on average more than 60% greater than what was predicted by the systems of equations developed in this study.

Because the model specif ications for component equations in this study aligned with the log production processof typical clear-fell harvesting operations, the two systems of additive equations (Eqs. 6 and 7) are not directly comparable to other existing stand level systems of additive equations that predict the biological or structural component biomass ofP. radiataplantations as described in Bi et al. ( 2010)and Castedo-Dorado et al. ( 2012). Although predictions of component biomass are not comparable, those of total aboveground stand biomass can readily be compared. The three systems of equations developed by Bi et al. ( 2010)were intended for general worldwide as well as countryspecif ic applications in Australia and New Zealand. They were based on published stand level biomass data from plantations less than 5 years old to rotation age, but with an overwhelming majority concentrating in younger age classes. In comparison to the two systems of equations (Eqs. 6 and 7)developed in this study, the three, systems of equations for general use and for plantations in Australia and New Zealand overestimated the total aboveground stand biomass by an average of 11.2%, 21.5%, and 9.8% across the 61 plots.By contrast, the system of biomass equations developed by Castedo-Dorado et al. ( 2012) forP. radiataplantations in northwest Spain showed only a slight underestimation of 0.5% when averaged across the 61 plots. These comparative dif ferences may need to be further examined to evaluate if the systems of equations developed by Bi et al. ( 2010) need to be improved and updated with additional biomass data from rotation age stands.

Fig. 7 Multi-panel display of observed component and total aboveground stand biomass in fresh and dry weight plotted against their predicted values from the system of equations that did not include dummy variables for stand types (Eq. 6).In each panel the diagonal line of unity was shown together with the 90% upper and lower conf idence limits of prediction error that were derived from Eq. ( 18) using parameter values in Table 7

Table 8 Estimated scale factors2 in log form and exponents( b) of the prediction error variance functions for the stand type-specif ic system of additive equations (Eq. 7). The dummy variable I equals 1 for thinned stands and 0 for unthinned stands. θs is Snowdon’s bias correction factor, p5 and p95 are the f ifth and ninety-f ifth percentiles of the weighted prediction errors. Two sets of estimates are shown for fresh and dry weight predictions of component and total aboveground stand biomass

Table 8 Estimated scale factors2 in log form and exponents( b) of the prediction error variance functions for the stand type-specif ic system of additive equations (Eq. 7). The dummy variable I equals 1 for thinned stands and 0 for unthinned stands. θs is Snowdon’s bias correction factor, p5 and p95 are the f ifth and ninety-f ifth percentiles of the weighted prediction errors. Two sets of estimates are shown for fresh and dry weight predictions of component and total aboveground stand biomass

?

Fig. 8 Multi-panel display of observed component and total aboveground stand biomass in fresh and dry weight plotted against their predicted values from the system of equations that incorporated dummy variables for stand types (Eq. 7). In each panel the diagonal line of unity was shown together with the 90% upper and lower conf idence limits of prediction error for unthinned (red lines) andthinned (blue lines) stands. The conf idence limits were derived from Eq. ( 18) using parameter values in Table 8

Extending the work of Wang et al. ( 2017) on individual trees to stand level, this study provided the f irst example of how stand level product, residue and their sub-component biomass of rotation-ageP. radiataplantations could be estimated through a system of equations with either an additive and/or allocative model specif ication. Of the two systems of equations that are recommended for use, one system (Eq. 6) was intended for more general application in plantations where stand density management regimes were substantially dif ferent from the stand types in our study,while the other system (Eq. 7) was intended for stand typespecif ic applications in plantations in NSW and other states of Australia where the silvicultural regimes are the same as,or similar to, the T0, T1 and T2 stands. When using either of the two systems of equations to estimate log product and harvest residue biomass of a rotation-age stand, it would be prudent to compare its stand attributes with those of the three stand types in this study. The average and range of stand density, basal area, dominant height tabulated for each stand type in Wang et al. ( 2017) would serve this purpose.In addition, it should be kept in mind that the two systems of equations were developed for cut-to-length harvesting with no on-site debarking and so may not be suitable for other harvesting methods such as whole tree harvesting with on-site debarking.

The two systems of equations provide reliable estimates of not only the total amount of product and residue biomass but also their compositions across the stand types. The thinned stands had a greater proportion of product biomass in sawlogs than the unthinned stands. In unthinned stands, a greater proportion of residue biomass potentially available for harvesting was observed and predicted to be in short of fcut and waste sections (Figs. 4 and 6), while more residue biomass was found in treetops and branches in the thinned stands. As using forest harvest residue biomass for bioenergy has increasingly become integrated into commercial forestry(Hall 2002; Campbell and Anderson 2019; Hanssen et al.2019; Van Holsbeeck et al. 2020), reliable estimates of this nature will assist harvest and management planning for clearfell operations that integrate cut-to-length log production with residue harvesting ( Ghaf fariyan et al. 2012, 2015).Stump biomass as a component of harvest residues inP.radiataplantations is unlikely to be collected for bioenergy purposes at present, unlike in some other forests ( Persson and Egnell 2018; Eufrade-Junior et al. 2020). However, it is an essential part of the predicted total aboveground stand biomass, from which root biomass can be estimated by applying a root/shoot ratio of 0.2 as recommended by Beets et al. ( 2007) forP. radiatastands across all stand ages and sites.

Conclusions

The use of harvest residue biomass for renewable energy generation has become an integral part of the sustainable management ofP. radiataplantations in Australia and other major growing countries. To facilitate this trend, this study developed the f irst systems of equations for predicting stand level product, residue, and their sub-component biomasses in fresh and dry weight of rotation-age plantations to be clear felled by cut-to-length harvesters. Two systems of additive equations are recommended for use based on their comparative predictive performances: one (Eq. 6) for general and the other (Eq. 7) for stand type specif ic applications. Both systems of equations are driven by stand level predictor variables that are commonly obtained from inventory plots and outputs from conventional growth and yield models at the same spatial scale. Thus, these systems of equations could readily be incorporated into forest resource information systems to assist the sustainable management ofP. radiataplantations.

AcknowledgementsThe ef forts of Mirella Blasi and Rebecca Coburn in plot establishment, tree measurements and destructive sampling were critical to the successful undertaking of this research. Gavin Jef fries,Mike Freeman, William Shearman of the Northern Softwood Region of the Forestry Corporation of NSW provided support to the project.

Declaration

Conf lict of interestThe author declares that they have no conf lict of interest.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http:// creat iveco mmons. org/ licen ses/ by/4. 0/.