烧蚀磨损理论下多参数变化对火炮内弹道性能的影响分析

蒋俊君,陆 欣

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

火炮身管烧蚀现象普遍存在于各类型火炮的射击过程中,烧蚀现象的出现会引起火炮内膛结构发生改变,导致火炮内弹道起始条件变化,进而对火炮的使用性能、弹道性能产生不利的影响。目前火炮烧蚀内弹道仿真研究主要基于经典内弹道理论,在发射药及其燃烧规律、弹丸启动压力和炮膛结构差异方面展开研究。有学者研究表明:火药燃气的爆热越大炮膛烧蚀越严重,例如,某火炮使用爆热为5.338 MJ/kg的火药作为发射药,其寿命约为1 200发;而改用3.416 MJ/kg的发射药,其寿命延长至3 000发[1-2]。张喜发等[2]建立了启动压力与起始部膛线剩余高度的函数关系,用来计算烧蚀磨损后弹丸的启动压力,提供了火炮烧蚀内弹道仿真方法。金文奇等[3]引入了烧蚀磨损容积增量缩径长,建立了全膛烧蚀磨损特征的内弹道模型,利用数值解法进行了内弹道仿真计算,仿真精度高于常规火炮烧蚀内弹道方法,拓展了烧蚀磨损内弹道理论。还有学者利用少量试验数据,建立数学预测模型预测不同射弹数引起身管内膛烧蚀量。文献[4-5]分别提出BP神经网络和随机Wiener的方法对身管烧蚀量进行了预测,结果表明:预测数据与试验数据基本吻合,避免了为掌握烧蚀规律需要对火炮进行全寿命试验所花费的大量人力、物力。

以上学者研究了火炮烧蚀量计算方法及其对内弹道性能的影响。本文以某火炮为研究对象,将火炮烧蚀磨损量与射弹数相联系,研究身管磨损量对下一发射击过程内弹道性能的影响。建立火炮身管烧蚀模型,通过编程计算得到一定射弹数条件下火炮烧蚀磨损量及其对应的启动压力。通过计算拟合得到火炮烧蚀磨损量与射弹数之间的函数关系。在此基础上研究了不同启动压力对火炮初速、最大膛压的影响。

1 数值模型

1.1 物理模型

身管是将药室内火药能量转换为弹丸动能的装置[6]。随着火炮射弹数增加,身管烧蚀磨损量不断累积,导致身管内径不断增大,弹丸启动压力降低,使得火药燃烧规律发生变化:火药气体产生速率、压力增长率和火药能量利用率降低,导致最大膛压下降、燃气速度减小,造成火炮初速减退。故对于装备部队的制式火炮,身管的烧蚀磨损是其内弹道性能变化的主要原因[7]。根据烧蚀磨损的特点,在建模时遵循如下基本假设:

①药粒均在平均压力下燃烧,且火药燃烧遵循几何燃烧定律和燃速定律。

②弹带挤进膛线是瞬时完成,且挤进膛线后密封良好。

③用系数φ来考虑其他的次要功。

④内膛表面热散失用减小火药力f或增加比热比k的方法间接修正。

⑤火药燃气服从诺贝尔-阿贝尔状态方程。

⑥火药力f、余容α及比热比k均视为常数。

1.2 数学模型

要分析不同烧蚀磨损量对火炮内弹道性能的影响,首先,应求解内弹道方程组。

依据经典内弹道模型,建立火炮烧蚀磨损后内弹道方程组:

(1)

式中:χ,χs,λ,λs,μ为火药形状特征量;ψ为发射药已燃百分比;Z,Zk为发射药已燃相对厚度;μ1为燃速系数;2e1为弧厚;l为弹丸行程;n为燃速指数;φ为次要功系数;v为弹丸速度;S为炮膛横截面积;p为膛内气体压力;m为弹丸质量;l0为药室容积缩径长;lψ为药室自由容积缩径长;V0为新炮药室容积,ρz=ω/V0,ω为装药量,α、ρ、f分别为火药燃气余容、密度、火药力,θ为绝热指数参量。

后效期弹丸飞出炮口断面后,火药气体从膛内流出,直到膛内压力下降到约0.2 MPa,火炮的后效期才结束。后效期温度T、压力p、密度ρ可通过以下公式计算。

(2)

式中:Tk、pk、ρk分别为内弹道结束时期火药燃气温度、压力、密度,B1为后效期作用系数,n1为多变指数。

根据式(1)和式(2)可求出火炮射击过程身管内壁温度和火药气体对流换热系数,将其代入式(3)[8]得到身管烧蚀量。由于本文采用内弹道零维模型,故计算所得烧蚀量为射击引起烧蚀量的平均值。

(3)

式中:t1为身管内膛表面温度达到熔点的时间,t2为表面温度降低到熔点的时间,Ts为身管材料初温,ρs为身管密度,T为火药燃气温度,Tp为身管熔点,h为燃气与身管内壁之间对流换热系数。由式(3)可以计算出某一射击过程条件下身管烧蚀磨损量S′。径向磨损量Δd=2S′。

文献[2]给出了火炮烧蚀磨损后的启动压力计算公式:

(4)

式中:N′为动载系数;K为弹带长度修正系数;d2为弹道直径;d4=d1-2atshi/(a+b),d1、a、b分别为阴线直径、阳线宽、阴线宽,tshi=tsh-Δd/2为剩余膛线深,tsh为膛线高;σs为弹带材料屈服极限;As,Bs分别为坡膛起点和终点结构参数。

通过以上步骤计算出火炮间歇发射一定数量弹丸后的磨损量,再求出发射下一发弹丸的启动压力,代入内弹道方程研究火炮烧蚀磨损量对内弹道性能影响。

2 结果与讨论

2.1 初始参数

以某火炮为研究对象进行数值模拟,计算参数如表1所示,表中,ρp为火药密度,Lg为弹丸行程长。采用龙格-库塔法对内弹道方程求解,根据气体状态方程计算出燃气温度、密度。再根据马蒙托夫经验公式计算对流换热系数。

表1 某火炮装填与结构参数

2.2 弹丸启动压力计算

根据式(4)可以计算不同磨损程度下对应的启动压力,该型火炮计算启动压力参数如表2所示。

表2 某火炮启动压力相关计算参数

利用式(4)计算出启动压力随径向磨损量变化规律,如图1所示。

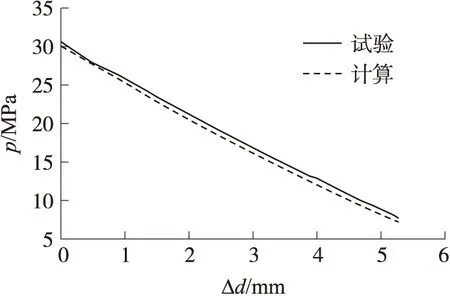
图1 p-Δd曲线计算值与实测值的比较

试验数据来自文献[2],当径向磨损量Δd=5.27 mm时所对应的启动压力为7.76 MPa,同磨损量条件下通过数值计算所得启动压力为7.14 MPa。从图中可以看出通过计算所得启动压力与试验误差较小,说明所建立的火炮烧蚀模型是合理的。

2.3 内弹道仿真与分析

模拟火炮自然射弹一定发数,每次射击过程都是待身管冷却至初始温度后再进行射击,基于该条件下得到径向磨损量Δd与射弹数N的函数关系,如图2所示。

图2 径向磨损量Δd与射弹数曲线

拟合后得出径向磨损量Δd与射弹数N的函数关系:

Δd=0.335+0.015N+5.67×10-6N2

(5)

2.4 烧蚀磨损对内弹道性能的影响

从图3可知,弹丸在膛内的速度随着身管磨损量增加不断下降,当磨损量Δd=3.56 mm时,炮口初速相较于新炮下降了3.7%。身管磨损量加剧会导致药室容积增加,火药燃气密度减小,做功能力减小,火药利用率降低;弹丸定位点前移,行程长减小。最终造成弹丸速度上升梯度变缓慢。

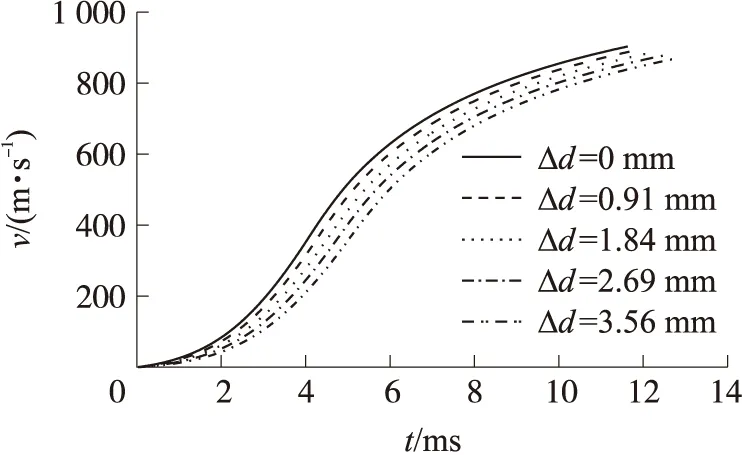
图3 不同身管磨损量条件下速度-时间曲线

从图4可知,随着身管烧蚀磨损量的增加,弹丸的启动压力不断下降,最大膛压也不断降低。当径向磨损量Δd=3.56mm时,最大膛压仅为新炮最大膛压的88.5%。膛压达到最大的时间和内弹道时间均随着烧蚀磨损加剧而延迟。

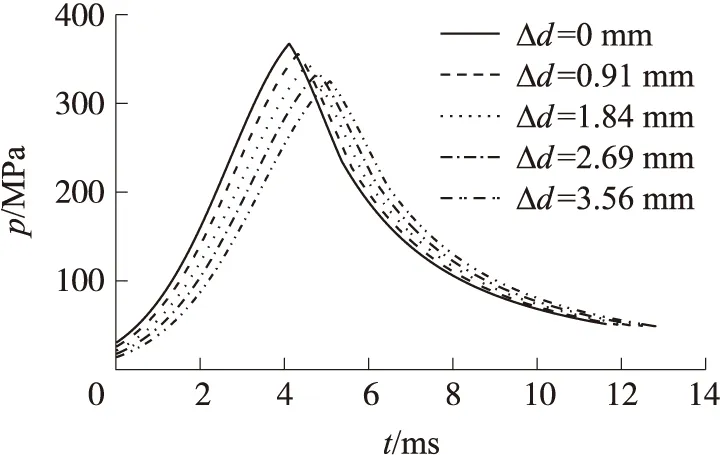
图4 不同身管磨损量条件下膛压-时间曲线

从图5可知,随着火炮烧蚀磨损量的增加,弹丸的速度和炮口初速不断降低,变化速率也较为缓慢,新炮条件下弹丸速度随行程变化最快。

图5 不同身管磨损量条件下速度-行程曲线

从图6可知,随着火炮烧蚀磨损程度加剧,火炮最大膛压点向炮口方向移动,且数值上不断减小。新炮条件下最快达到压力最高点。达到最高压力点之后,新炮膛内压力随行程变化较快,而随着磨损量的增加,压力随行程变化较为缓慢。

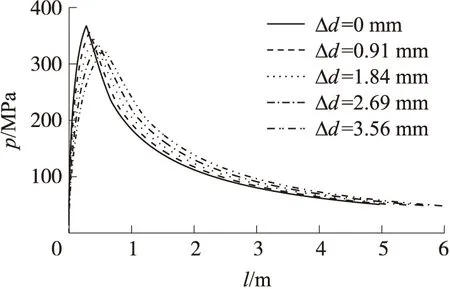
图6 不同身管磨损量条件下压力-行程曲线

作出径向磨损量、火炮相对初速下降百分比Δv0/v0、火炮相对最大膛压下降百分比Δpm0/pm0函数图,如图7和图8所示。

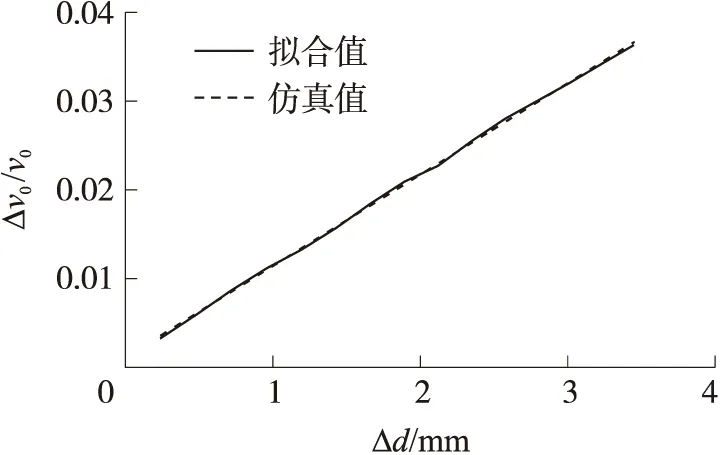
图7 不同身管磨损量条件火炮相对初速下降百分比曲线

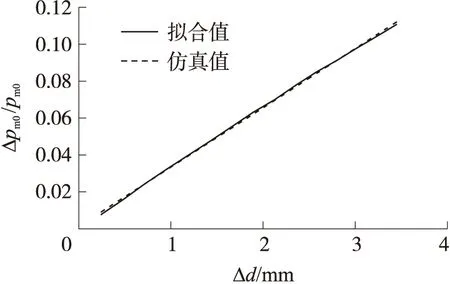
图8 不同身管磨损量条件火炮相对最大膛压下降百分比曲线

从图7可以看出,火炮相对初速下降百分比随磨损量的增加而增大,且二者成线性相关,经过拟合得出火炮相对初速下降量预测数学模型:

Δv0/v0=0.001+0.010Δd

(6)

式中:v0为新炮条件弹丸初速,Δv0为不同磨损条件下弹丸初速同新炮条件下弹丸初速差值。

从图8可以看出,火炮相对最大膛压下降百分比随磨损量的增加而增大,且二者成线性相关,经过拟合得出火炮相对最大膛压下降量预测数学模型:

Δpm0/pm0=0.001 58+0.032 1Δd

(7)

式中:pm0为新炮条件下最大膛压,Δpm0为不同磨损条件下最大膛压同新炮条件下最大膛压差值。通过式(5)可以计算出任意射弹数条件下对应的磨损量,基于此条件可以研究对下一射击过程内弹道性能的影响。

3 装填参数对烧蚀内弹道性能影响研究

3.1 火药力对烧蚀内弹道性能影响

其他条件相同的情况下仅改变火药力来研究不同磨损量情况下炮口相对初速下降百分比。

从图9可以看出,当火药力增大,随着径向磨损量增加,火炮初速相对减退量减小。同一磨损量条件下,增大火药力,相对初速减退量会降低。

图9 不同火药力条件下炮口相对初速下降百分比曲线

3.2 装药量对烧蚀内弹道性能影响

为了发挥火炮火力的机动性,通常选择改变装药量使弹丸获得不同的初速。不同装药量条件下身管磨损程度不同引起的初速变化情况需要被研究。图10为不同装药量条件下炮口相对初速下降百分比与径向磨损量关系图。

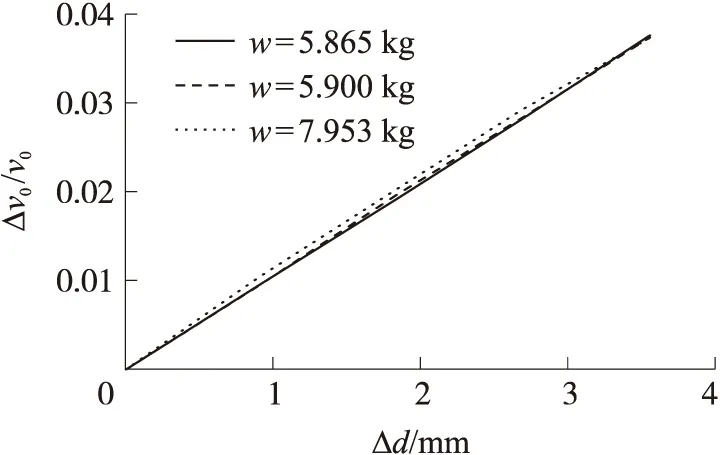
图10 不同装药量条件下炮口相对初速下降百分比曲线

从图10可以看出,当装药量增大时,随着磨损程度加剧,炮口相对初速下降百分比逐步减小。

4 烧蚀磨损对火炮寿命影响

内膛烧蚀磨损使火炮内弹道性能不断下降、最大射程减小、地面密集度和立靶密集度散布增大 、引线连续瞎火、出现近弹、早炸等现象,最终导致身管寿命终止。当出现初速下降过大(如超过60 m/s左右),或弹丸摆动过大时,身管就将报废[8]。火炮内膛最大磨损量Δdmax是判别身管寿命的重要参数,最大径向磨损量和膛线高度存在非常好的对应关系,二者可以建立起稳定的函数关系[2],其表达式为

Δdmax=2(tsh+A1)

(8)

式中:tsh为火炮膛线高度,对于深膛线的中、大口径火炮,取值为1.0～1.6mm,本文取A1=1.1用作计算该火炮身管的最大径向磨损量,由此计算得出火炮寿命终止时对应的径向磨损量Δdmax=7.6 mm。对应的射弹数为420。再将其代入式(4)计算出身管寿命终止所对应的启动压力为3.78 MPa。代入内弹道方程组计算该条件下内弹道诸元。

图11为身管达到预测寿命和新炮条件下弹丸速度对比图,新炮达到炮口的速度为903 m/s,磨损量为7.6 mm火炮达到炮口速度为835 m/s,初速相比与新炮下降了7.53%,无法满足射击精度,达到身管报废标准。

图11 内膛最大磨损量与新炮条件下速度-时间曲线

5 结论

本文基于经典内弹道模型和火炮身管烧蚀理论,研究了一定射弹数条件下身管烧蚀磨损量对火炮内弹道性能的影响,得出以下结论:

①随着烧蚀磨损加剧,火炮内膛直径不断增加,使得弹丸定位点前移,导致弹丸行程长度减小,火药燃气对弹丸做功减小导致弹丸速度和火炮膛压均减小。

②当装药量增大时,随着磨损加剧,炮口相对初速减退量减小;当火药力增大,随着磨损加剧,炮口相对初速减退量增大。

③射弹数达到约420发时,径向磨损量Δdmax=7.6 mm,炮口初速相比于新炮下降了7.53%,无法满足射击精度,此时身管报废。本文仿真计算的结果可以为预测该火炮寿命提供依据。