侵爆战斗部对钢筋混凝土靶的侵彻能力计算方法
2021-12-24刘兴锋周兰伟朱荣刚
刘兴锋,周兰伟,朱荣刚
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国航空工业集团公司 洛阳光电设备研究所,河南 洛阳 471003)
钢筋混凝土是指通过在混凝土基体中加入钢筋而构成的一种复合材料。钢筋混凝土因其具有优异的力学性能,被广泛应用于各类军事和民用工程。钢筋混凝土靶的抗侵彻能力由混凝土和钢筋配置共同决定,钢筋排布造成靶板不同位置抗侵彻能力的差异性。研究战斗部对钢筋混凝土靶板侵彻能力的计算方法,对于侵彻类型战斗部的研制和防护结构的设计具有重要意义。
对钢筋混凝土侵彻问题的研究主要有3种方法:试验方法、理论分析方法和数值模拟方法。研究混凝土侵彻和贯穿问题中最早使用的是试验方法,在试验基础上得到了许多经验公式。如最早使用的Petry公式[1]、俄国的别列赞公式[2]、美国Sandia国家实验室提出的Young公式[3]、工程兵三所公式[4]等均可用于预测不同尺寸弹体对混凝土靶板的侵彻深度或贯穿速度。赵南等[5]开展的弹体高速侵彻钢筋混凝土试验的试验结果与Young公式基本一致。周阳等[6]基于侵爆战斗部对钢筋混凝土结构的侵彻以在楼房内部爆炸时的情况为例,评估了弹药对楼房的毁伤能力。理论分析方法中应用的模型主要有空腔膨胀模型和弹塑性流动力学模型。LUK和FORRESTAL[7-8]将空腔膨胀模型用于混凝土材料,认为材料的响应可以分为弹性区和塑性区,其使用球形空腔膨胀模型分别建立了卵形弹和半球形弹高速侵彻混凝土板的理论模型。刘志林等[9]在空腔膨胀模型的基础上,考虑钢筋在侵彻过程中对弹丸的阻力,建立了弹丸侵彻钢筋混凝土靶的工程解析模型。随着计算机技术的发展,数值模拟方法在侵彻问题中得到了广泛的应用。孟阳等[10]使用HJC混凝土损伤本构模型对钢筋混凝土靶板在冲击载荷下的响应进行了数值模拟,得到的弹道极限和剩余速度结果与试验数据吻合较好。KONG等[11]对K&C模型的强度进行了修正,并加入了拉伸损伤、应变率效应和拉压的不对称性,数值模拟结果在混凝土破坏和弹丸剩余速度方面与试验较为吻合。冯君等[12]基于LDPM离散单元建立钢筋混凝土数值计算模型,研究了侵彻位置对出靶速度的影响。
通常试验得到的经验公式形式比较简单且使用方便,但由于经验公式一般通过拟合试验数据获得,使用范围存在一定局限性。理论分析方法中的方程是基于物理和力学原理的抽象简化建立的,可以反映弹靶相互作用的主要机理,但是方程的推导及求解过程复杂,且模型简化过程中会忽略钢筋配置方式、命中靶板位置等细节。数值模拟方法将弹、靶离散成单元或粒子,通过赋予单元或粒子基本的力学特性,然后利用质能守恒方程、材料本构关系并结合初始边界条件建立方程组进行求解,数值模拟结果的准确性严重依赖于本构模型和失效准则。
在钢筋混凝土侵彻问题相关的研究中,通常将钢筋以配筋率的形式均匀分布在混凝土中或将钢筋层等效为一定厚度的均质薄钢板,这无法反映具体钢筋配置方式和命中位置对侵彻能力的影响。对于钢筋混凝土这类非均质材料,命中位置对侵彻能力的影响尤为明显。极限穿透速度是评价战斗部性能的一个重要指标,而使用平均极限穿透速度作为评价指标时更加全面。为此,本文通过试验和数值模拟相结合的方法,综合考虑命中位置和弹靶尺寸参数的影响,通过3个典型命中位置研究战斗部对钢筋混凝土靶板的侵彻能力计算方法。
1 侵爆战斗部侵彻钢筋混凝土靶试验
根据侵彻能力计算方法研究的需要,设计并进行了侵爆战斗部侵彻钢筋混凝土靶板的试验研究。
1.1 战斗部
战斗部弹体材料为高强度35CrMnSi;主体为圆柱形,外径86 mm,总长209 mm;头部为卵形,长度110 mm。战斗部外形及弹体结构分别如图1和图2所示。战斗部总质量为4.2 kg,弹体内有模拟炸药装药和模拟引信,模拟引信质量为0.189 kg,模拟炸药装药质量为0.59 kg。

图1 战斗部外形

图2 弹体结构
1.2 钢筋混凝土靶板
钢筋混凝土靶板尺寸为1 600 mm×1 600 mm×200 mm,浇筑时间为1.5个月,混凝土标号为C35,内部为符合三级标准(HRB400以上)的直径12 mm螺纹钢筋。钢筋沿厚度方向布置成一层,平面上呈网状结构,钢筋间隔为250 mm×250 mm,共14根钢筋(7×7排布),最外侧钢筋距边缘50 mm,钢筋距上靶面100 mm,钢筋混凝土靶板结构尺寸如图3所示。

图3 钢筋混凝土靶板的结构尺寸
1.3 试验结果
通过大口径火炮发射2发战斗部。试验中战斗部垂直撞击靶板,第一发试验弹撞靶速度为288 m/s,战斗部穿透了钢筋混凝土靶板,靶后剩余速度为102 m/s;第二发试验弹撞靶速度为258 m/s,战斗部穿透了钢筋混凝土靶板,靶后剩余速度为64 m/s。靶板损伤情况如图4所示。由钢筋混凝土靶板的毁伤状态可知,战斗部均命中单根钢筋,钢筋产生了较大弯曲变形,第一发战斗部造成单根钢筋断裂。混凝土穿孔近似为圆形,战斗部的贯穿造成靶板前后表面大面积混凝土崩落。战斗部表面有少量磨损,但质量损失很小,可忽略不计。

图4 靶板损伤情况
2 数值模拟分析
建立战斗部和靶板的有限元模型,并根据试验结果验证了计算模型的正确性,分析侵彻过程中钢筋混凝土靶的响应状态。
2.1 有限元模型
根据试验情况,使用有限元软件ANSYS/LS-DYNA建立侵爆战斗部和分离式钢筋混凝土靶板的有限元模型,使用梁单元对钢筋划分网格,其余结构均使用实体单元划分网格。在模拟战斗部后端增加配重块替代模拟引信,通过耦合算法定义钢筋和混凝土的相互作用。鉴于梁单元的力学性能,梁单元只能在长度方向上分割,本次建模时均采用了完整模型。战斗部侵彻钢筋混凝土靶板的有限元模型如图5所示(分别为剖去二分之一战斗部和四分之三混凝土)。

图5 有限元计算模型
2.2 材料模型及参数
钢筋对混凝土起到强化作用,能够大幅度提高混凝土靶板的抗侵彻性能。钢筋耦合在混凝土中,在侵彻过程中会发生大变形、拉断情况,随动强化作用明显,须考虑材料的应变率效应。战斗部壳体材料为高强度钢,计算时采用随动硬化模型描述弹体和钢筋材料的力学行为,由式(1)定义其应变率效应。
(1)

弹体与钢筋的材料参数如表1所示,表中,ρ为材料密度;E为弹性模量;μ为泊松比;εs为失效应变;Et为切线模量。

表1 弹体和钢筋的材料参数

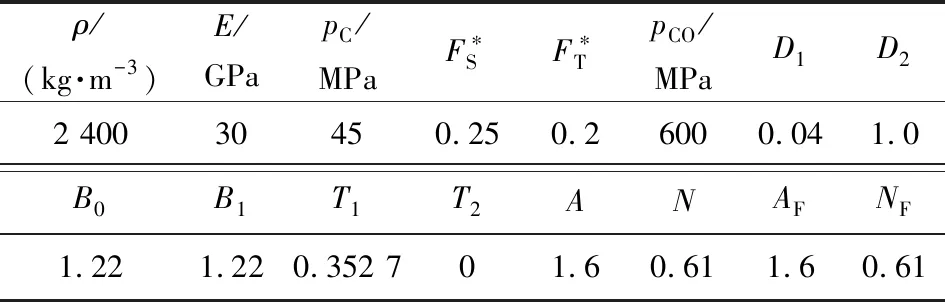
表2 混凝土材料参数
2.3 有限元计算结果以及与试验的对比
按照试验中战斗部的着靶状态和速度,计算了战斗部对钢筋混凝土靶板的侵彻。战斗部以288 m/s的撞靶速度侵彻钢筋混凝土靶板单根钢筋中心处的侵彻过程如图6所示。
从图6可以观察到侵彻过程中钢筋和混凝土靶板的响应。100 μs时,战斗部在混凝土表面开坑。随着侵彻深度的增大,混凝土内裂纹范围逐渐增大。370 μs时,战斗部头部已完全侵入混凝土,由于钢筋的约束作用,钢筋网格面阻碍了裂纹的扩展,增强了混凝土抗侵彻的能力。同时,靶板背面的混凝土在拉应力作用下产生裂纹。500 μs时,混凝土中的裂纹已扩展至整个厚度方向,战斗部头部与钢筋接触,钢筋产生较大变形。1 300 μs时钢筋已断裂,此时战斗部完全侵入混凝土靶板,混凝土靶板背面产生较大面积的鼓包和裂纹。2 000 μs时,混凝土靶板正面入口处有混凝土崩落,钢筋断裂后产生较大程度的弯曲变形。3 000 μs时,战斗部穿出混凝土靶板,靶板背面产生大面积混凝土的崩落,混凝土背面崩落尺寸大于正面崩落尺寸。
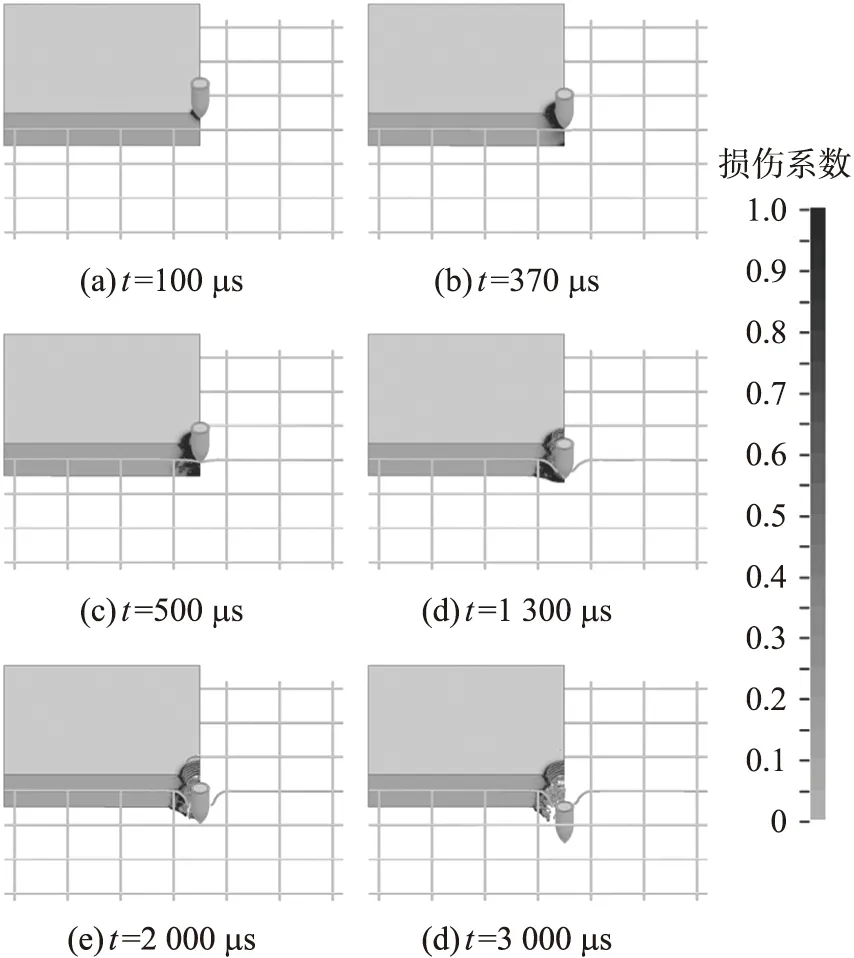
图6 战斗部侵彻钢筋混凝土过程
战斗部分别以288 m/s和258 m/s撞靶速度侵彻靶板,加速度、速度和位移曲线如图7所示。

图7 战斗部运动曲线
战斗部接触到混凝土表面后在混凝土表面开坑,侵彻阻力随战斗部头部与靶板的接触面积的增大而增大,减加速度迅速增大。1 000 μs左右时,混凝土基体基本失效,战斗部加速度趋于0,速度变化平缓。此后,战斗部近似以匀速穿出钢筋混凝土靶板,并且弹体仍保持完整。
有限元模型的计算结果及与试验的对比见表3,表中,v0为初速;vs为战斗部穿透靶板后的剩余速度;δ为仿真值与试验值的相对误差。由数值计算结果与试验结果的对比可知,剩余速度相对误差在15%以内,验证了数值计算模型的正确性。可以采用上述模型进行计算,预测战斗部贯穿钢筋混凝土靶板后的剩余速度,并得到战斗部对钢筋混凝土靶板的极限穿透速度。

表3 数值计算结果及与试验的对比
3 战斗部命中靶板位置对极限穿透速度的影响
极限穿透速度是评价战斗部性能的一个重要指标,可将其作为战斗部侵彻能力的一个表征量。由于钢筋混凝土靶板为非均质材料,极限穿透速度与战斗部命中靶板的位置有关,因此需根据靶板特点研究命中典型位置对极限穿透速度的影响。
3.1 命中典型位置的确定
为使计算得到的极限穿透速度具有一定的代表性,更好地评价战斗部命中靶板位置对极限穿透速度的影响,结合钢筋混凝土靶板的结构特点,选择3个典型命中位置:钢筋节点、单根钢筋中心和钢筋网格中心,如图8所示。

图8 战斗部命中靶板位置
3.2 命中不同位置时战斗部极限穿透速度
根据上节所确定的战斗部的命中位置,使用升降法分别使战斗部以不同的速度垂直侵彻钢筋混凝土靶板。由于数值计算中给定的初始撞靶速度是离散值,穿透靶板的最小撞靶速度与未穿透靶板的最大撞靶速度差值不超过Δv(文中取5m/s)时,停止下一组数值计算。取穿透靶板的最小撞靶速度及剩余速度,根据能量守恒原理将所计算速度作为该命中位置的极限穿透速度vb,则极限穿透速度的绝对误差小于Δv,相对误差小于Δv/vb,计算结果见表4(“-”表示未穿透)。由计算结果可知,战斗部命中单根钢筋处和钢筋节点处的极限穿透速度分别比命中网格中心处的极限穿透速度高15.9%和29.2%,命中位置对极限穿透速度的影响明显。

表4 极限穿透速度计算结果
4 战斗部侵彻靶板的平均极限穿透速度
由第3节计算可知,命中位置对极限穿透速度影响明显。将命中区域各点的极限穿透速度加权计算得到的速度称为平均极限穿透速度,并将其作为战斗部侵彻能力的评价指标。在本节中综合考虑命中位置和弹靶尺寸参数的影响,通过3个典型命中位置研究战斗部对钢筋混凝土靶板的平均极限穿透速度计算方法。
4.1 战斗部极限穿透速度函数的建立
结合工程中常使用的钢筋排布方式,假设钢筋混凝土靶板的钢筋网格为相同的矩形,尺寸为l1×l2。不考虑钢筋直径和靶板边界。矩形钢筋网格具有对称性,仅需分析四分之一钢筋网格区域(含边界)。以钢筋节点为坐标原点,坐标轴与钢筋轴线重合建立如图9所示的平面直角坐标系Oxy,记战斗部命中靶板(x,y)处的极限穿透速度为vb(x,y)。根据战斗部直径d与网格尺寸的大小关系分为2种情况:d 图9 坐标系及计算域 当d 战斗部命中钢筋时与钢筋的接触长度是连续变化的,对于等厚度的钢筋混凝土靶板,做出以下假设:速度函数v(x,y)具有连续性,且在各区域Ωi(i=1,2,3,…,7)内为线性分布,即: v(x,y)=kix+miy+bi(x,y)∈Ωi (2) 式中:ki,mi,bi(i=1,2,…,7)为对应区域Ωi时函数待求参数。 根据第3节中确定的3个典型命中位置,记钢筋节点处、单根钢筋中心处、网格中心处战斗部对靶板的极限穿透速度分别为vb(0,0)=v1,vb(l1/2,0)=vb(0,l2/2)=v2,vb(l1/2,l2/2)=v3。当l1≠l2时,取命中较短单根钢筋中心处的极限穿透速度为v2。 当d (3) 当d≥min{l1,l2}时,可解得极限穿透速度函数表达式为 (4) 为了验证极限穿透速度函数的正确性,使用已验证的有限元模型计算d 表5 函数值与数值计算的对比 由表5中的数值计算结果可知,战斗部轴线穿过单根钢筋时,随着命中点与钢筋节点距离的减小,极限穿透速度略微增大。vb(x,y)函数值与数值计算结果相对误差的绝对值均在3%以内,验证了极限穿透速度函数值与数值计算结果的一致性。 战斗部命中钢筋混凝土靶板的位置具有随机性,假设命中各点的概率相等,则战斗部穿透钢筋混凝土靶板的平均极限穿透速度为 (5) 式中:Ω为积分区域;S为积分区域总面积。 分别代入2种情况下的战斗部极限穿透速度表达式,并化简得到战斗部的平均极限穿透速度为 (6) 本文提出了一种计算侵爆战斗部对钢筋混凝土靶侵彻能力的方法,该方法基于战斗部侵彻靶板3个典型位置的极限穿透速度得到战斗部的平均极限穿透速度,综合考虑了命中位置及弹、靶尺寸的影响,将其作为战斗部侵彻能力的评价指标时更加全面。此外还得到以下结论: ①战斗部命中靶板单根钢筋处和钢筋节点处的极限穿透速度分别比命中网格中心处的极限穿透速度高15.9%和29.2%,研究战斗部侵彻能力时要考虑命中位置的影响; ②基于3个典型命中位置的极限穿透速度建立极限穿透速度函数,并验证了速度函数值与数值计算结果具有良好的一致性。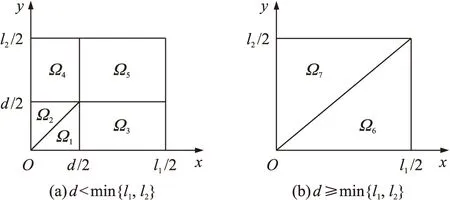


4.2 极限穿透速度函数验证

4.3 平均极限穿透速度计算

5 结论
