旋转稳定弹的自转角加速度特性

常思江,王中原,陈 琦,李东阳

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

旋转稳定弹是一类由线膛火炮发射、通过高速自旋形成陀螺效应来保持稳定飞行的弹丸,具有阻力小、结构简单、定向性好等特点。国内外仍大量装备并经常使用旋转稳定弹,从5.6 mm到155 mm等一系列口径上均有对应的装备。旋转稳定弹在飞行过程中围绕自身纵轴高速旋转(小口径枪弹的转速可达2 500 r/s),导致其具有一些典型的外弹道特性,如反映动力平衡角影响的偏流特性、高频与低频圆运动叠加的攻角特性等。因此,旋转稳定弹的转速特性一直以来都是外弹道领域的重要研究内容。一般外弹道学教科书中[1-2],主要研究了旋转稳定弹的炮口转速和转速的衰减特性,利用这些特性可开展一些应用,如通过分析炮弹高转速产生的离心惯性力指导引信解保机构及过载特性设计。近年来,针对一些特殊应用,研究人员也开展了相关研究。文献[3]针对前、后两体差动自旋的有控旋转稳定弹,进行了转速特性研究。文献[4]针对细长体弹箭,研究了不同转速对共振的影响。文献[5]研究了超高速炮射动能弹的转速特性,旨在指导其后体结构的设计与优化。文献[6]为了分析某榴弹引信弹道炸的原因,也对其转速特性进行了研究。随着传感器及信息融合技术的不断发展,可测得的旋转稳定弹弹道参数也越来越多,利用这些参数的变化特性,可以开展更多的应用和研究。

本文基于外弹道学理论,从旋转稳定弹的自转动力学微分方程入手,研究旋转稳定弹自转角加速度在弹道上的变化特性,并利用若干典型旋转稳定弹的数据进行分析和验证,以期为旋转稳定弹丸外弹道特性的深入应用提供理论依据。

1 理论分析

根据外弹道理论[1-2],旋转稳定弹自转动力学可采用如下简化微分方程表示:

(1)

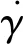
根据自转动力学微分方程(1),可考察旋转稳定弹自转角加速度的一阶导数,即:

(2)

将式(1)代入上式等号右端表达式,可得:

(3)

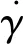
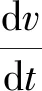
(4)

根据外弹道质点弹道方程[2],将dv/dt的表达式代入上式,可得:

(5)

式中:g为重力加速度;θ为弹道倾角;阻力参数bx=cxρS/(2m),其中m为弹丸质量,cx为弹丸阻力系数。

根据式(5)可知,旋转稳定弹自转角加速度的一阶导数是否为0,主要取决于弹道上弹丸的阻力参数、极阻尼力矩参数及重力加速度沿速度方向分量这三者的关系。当式(5)成立,表示阻力、极阻尼力矩及重力加速度三者形成平衡关系。当角加速度一阶导数为0,表明旋转稳定弹的自转角加速度出现极值点。由于阻力参数bx和极阻尼力矩参数kxz均为正数,欲使式(5)成立,唯有当θ<0,即弹道降弧段上才有可能实现。

进一步考察角加速度二阶导数,即:

(6)

将上式整理,可得:

(7)

当自转角加速度出现极值点时,式(4)成立,将其代入式(7)可得:

(8)

将式(5)代入上式,经整理可得:

(9)

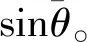
根据二次函数的求根公式,可得:

(10)

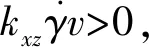
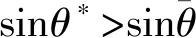
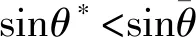
从外弹道学角度,如果某个弹道参数在弹道上存在极值点,将是比较有用的特性。譬如,外弹道学中的空气弹道特性,即弹丸在过顶点后降弧段上会出现速度极小值。了解和掌握这些特性,对于弹道的求解或计算、试验数据的判断和处理都是非常有益的[2]。

2 实例计算与分析

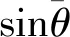
本节选取7.82 mm枪弹[7]、105 mm榴弹[7]、某76 mm、某130 mm以及某155 mm旋转稳定弹作为算例,开展外弹道计算,所用初速如表1所示。

表1 外弹道计算用初速值

计算结果如图1～图6所示,图中,θ0为射角。图1和图2为小射角下(5°和10°)各弹丸的降弧段自转角加速度及一阶导数曲线,图3和图4为中射角下(30°)各弹丸的降弧段自转角加速度及一阶导数曲线,图5和图6为大射角下(53°)各弹丸的降弧段自转角加速度及一阶导数曲线。

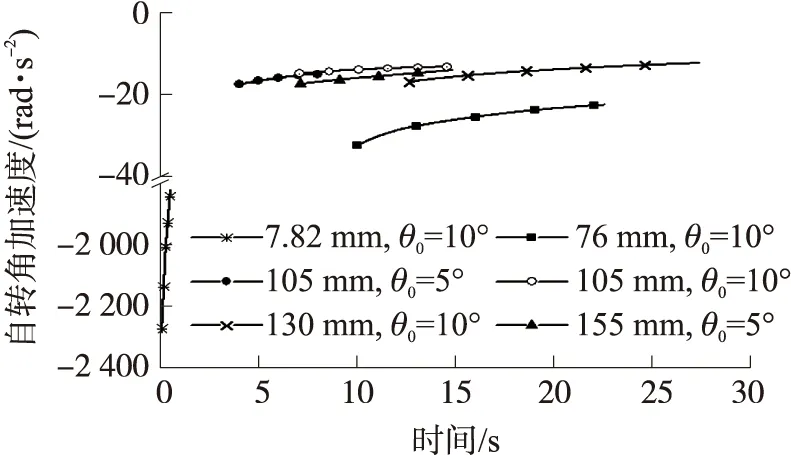
图1 小射角下各弹丸的自转角加速度

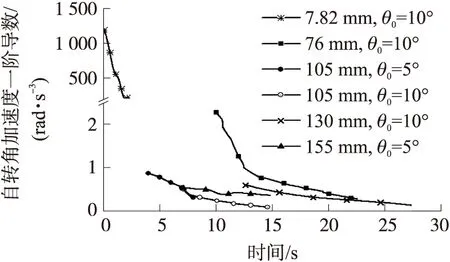
图2 小射角下各弹丸的自转角加速度一阶导数

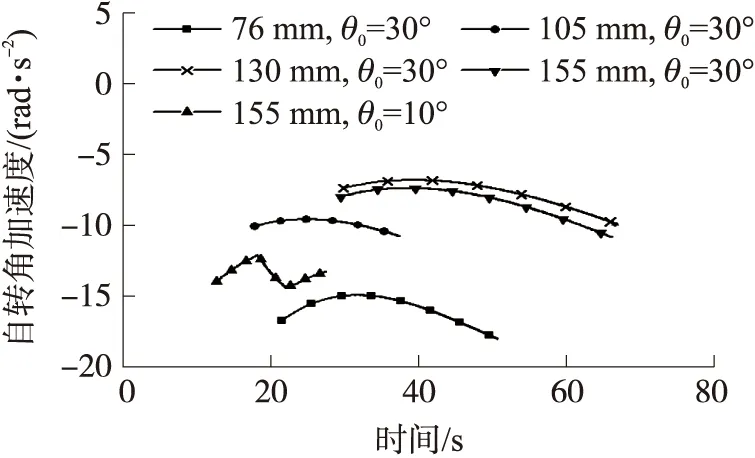
图3 中射角下各弹丸的自转角加速度

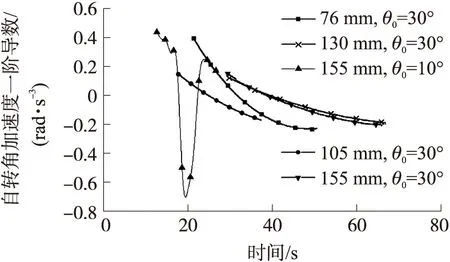
图4 中射角下各弹丸的自转角加速度一阶导数

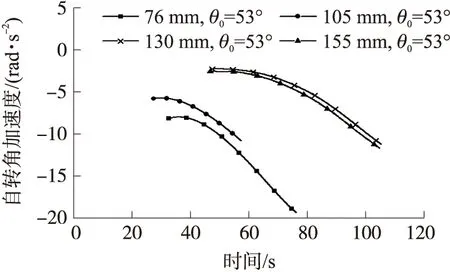
图5 大射角下各弹丸的自转角加速度

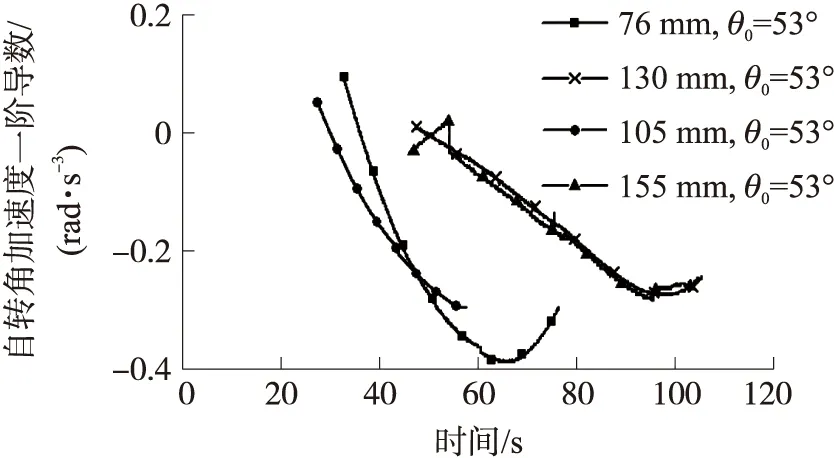
图6 大射角下各弹丸的自转角加速度一阶导数

从上述结果可知,对于不同弹丸和不同发射条件,自转角加速度是否会出现极值点(是否满足式(5)),不可一概而论。

如图1和图2所示,5种旋转稳定弹(除155 mm弹丸外)在射角5°或10°的小射角下,降弧度上的自转角加速度一阶导数均达不到零点,故自转角加速度曲线均无极值点。但155 mm弹丸在10°射角下,自转角加速度一阶导数却2次过零点(如图4),自转角加速度曲线出现2个极值点(如图3)。图3和图4中其他弹丸在30°中等射角下,降弧度上的自转角加速度一阶导数均过零点一次,自转角加速度曲线对应为极大值点。当射角增加到53°(大射角),如图5和图6所示,降弧度上的自转角加速度一阶导数过零点一次,自转角加速度曲线出现极大值。

当前对旋转稳定弹自转角加速度特性的研究尚属起步阶段,实际应用较少。自转角加速度本质上反映的是炮弹在高速旋转条件下的受力情况。而引信的设计、作用等往往与炮弹受力密切相关,故这方面会有相关应用。例如,目前已有传感器能够较为准确地测得旋转稳定炮弹的自转角加速度,当弹丸自转角加速度在弹道上存在拐点时,可作为引信识别弹道状态、触发后续动作的依据。根据上述研究结果,这一拐点是否存在与炮弹的射角有关,实际应用时应考虑炮弹自转角加速度在不同射角下的变化情形(如图1～图6所示曲线),采取合理的设计策略。

3 结论

本文利用外弹道学理论,对旋转稳定弹的自转角加速度特性开展了理论研究,可得到如下结论:

①在弹道降弧段上,当旋转稳定弹的速度、阻力系数、极阻尼力矩系数及弹道倾角等参数满足一定关系时,其自转角加速度的一阶导数会出现零点,由此推断其自转角加速度在弹道降弧段上有可能出现极值点。

③若弹丸的射角较小(如第2节算例中的5°或10°,但155 mm弹丸10°射角情形除外),弹道降弧段上的参数组合往往不能满足上述极值条件,自转角加速度曲线无极值点。因此,实际中如要应用自转角加速度的极值特性,必须要考虑射角条件,必要时可采用文中的式(5)和式(10)进行预判。

本文研究结果可为这一弹道特性的深入应用或相关产品开发提供必要的依据,也是对外弹道学中弹丸空气弹道特性结论的一个补充。