基于K近邻算法识别手写数字

2021-12-23马玉贤郭秀娟

吉林建筑大学学报 2021年6期

马玉贤，郭秀娟

吉林建筑大学电气与计算机学院,长春 130118

随着经济的发展,金融市场也日益加快,然而仍有大量的手写数字报告、汇款单等需要计算机进行识别管理,如果用计算机可以进行手写数字识别,将能节省大量的人力财力物力.所以,手写数字识别系统的开发对生产生活有重要的作用[1].K近邻算法是目前理论上比较成熟的算法,与其他算法相比直观简单,实用性较强,已经被广泛应用于各种分类问题[2],所以采用K近邻算法进行手写数字的识别有较好的效果.

1 K近邻算法的原理

K近邻算法属于分类与逻辑回归的算法,是机器学习中简单而且有效的算法.K近邻学习算法属于机器学习中的分类算法[3],工作机制相对来说比较简单:给定一个样本集合,也称作样本训练集,并且知道样本数据集中数据与其所属分类的对应关系.输入一个新的没有分类的数据之后,计算机提取数据的特征并且与数据集中的特征对比,找出与其特征相近的K个数据,在K个数据当中出现的分类频次最高的分类作为这个新数据的分类.

1.1 欧拉距离

通常情况下,使用欧拉距离公式来计算向量点的距离.关于欧拉距离的计算:

二维平面上两点A(x1,y1)与B(x2,y2)之间的欧拉距离:

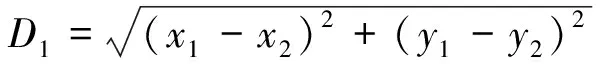
(1)

三维平面上两点A(x1,y1,z1)与B(x2,y2,z2)之间的欧拉距离:

(2)

N维向量A(x11,x12,…,x1n)与N维向量B(x21,x22,…,x2n)之间的欧拉距离:

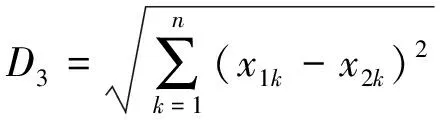
(3)

1.2 K值的选择

如果选择较小的K值,训练实例集合就会变小,训练的近似误差会变的很小,训练数据与输入的新数据相近才能有效果.K值变小的情况下,容易受到异常值的影响,更容易出现过拟合问题.选择较大的K值,训练实例会变大,训练的近似误差亦会变的很大,如果训练数据与新输入的新数据不相关也会产生不同效果,容易出现样本均衡的问题,使模型变得简单,出现欠拟合问题.所以,一般情况下将数据分为训练集和测试集来选取最优K值.

1.3 K近邻算法的一般步骤

(1) 获取训练数据集,抽取其特征.

(2) 数据集中一部分作为训练数据,一部分作为测试数据,用于验证.

(3) 选取一个K值,使用交叉验证法,即使用训练集和验证集选取最优K值.

(4) 计算与K值最相近的K个样本实例.

(5) 通过测试样本集判断准确性.

(6) 修改K值,跳到步骤(3),选取更准确的K值.

2 K近邻算法在手写识别系统中的实现

2.1 数据收集与图像预处理

由于Python使用简单,易于读写,支持面向对象的编程,所以算法的实现使用Python语言进行编程,采用Python3.7版本,以Pycharm Community作为集成开发环境.首先将需要识别的手写数字进行预处理,以满足算法的要求,把图片处理成黑白图片；其次将其转换为32×32的数组放入文本文档中；最后将图像转换成文本格式的文件(如图1所示).从sklearn手写数据集中收集2 000个从0到9的手写数字样本,用来训练分类器,另外收集900个测试数据样本,用来测试分类器的效果.

图1 手写数字数据集(部分) 图2 错误率随K值变化图3 运行结果(部分)Fig.1 Handwritten digit data set(partial) Fig.2 The error rate varies with the value of K Fig.3 Running results(partial)

2.2 准备数据与算法实现

将图片转换成向量,为了方便算法处理数据,把32×32的图像预处理为一个1×1 024的向量.然后对数据集中的每个点依次执行以下操作:

(1) 使用欧拉距离计算已知类别数据集中的点与当前点之间的距离.

(2) 计算出距离大小按照递增的次序对数据进行排序.

(3) 选取与当前点距离最小的K个点.

(4) 确定前K个点所在类别的出现频率.

(5) 确定前K个点出现频率最高的类别,作为此点的预测分类标签.

使用K近邻算法对预处理过的手写数字文件进行识别,取不同的K值,并且对错误个数与错误率进行统计,选取最优K值,识别错误率统计如图2所示.由实验统计可知,当K=3时,K值的错误率最低,因此选取K=3为最优K值.当K=3时,部分程序运行结果如图3所示.

2.3 结果分析

实验表明,当K=3时,运行结果中错误个数为10,准确率高达98.94 %,在算法中取不同的K值,实验准确率会有不同结果.所以,当采用交叉验证法选取合适的值时,K近邻算法对手写数字的识别会有较高的准确率,证明了该算法用于手写数字识别系统的可行性,且具有研究价值.各类别分类识别准确率见表1.

表1 各类别分类识别准确率Table 1 Classification and recognition accuracy of each category

3 K近邻算法优缺点分析

K近邻算法作为简单有效的分类算法,优点比较明显,新的数据集直接可以计算不必再重新训练,算法也比较简单,相对于其他算法来说比较容易实现,准确度较高,对异常值不敏感,容忍度较高.在手写数字识别方面,识别准确,误差小.但是在某些方面也存在缺陷,一是由于图像具有高维度特征,运算复杂,K近邻算法无法准确提取特征,通常情况下会受到干扰；二是,如果验证数字足够多则会出现一定量的误差.在执行此算法时,其训练时间复杂度为O(n),相比支持向量机等算法来说较低.但是在本次实验中,每次的距离运算均有210维度的运算,算法对测试向量需做高达两千多次的距离运算,这会导致计算复杂度过高,运行效率降低.样本数据过多时,要计算新数据到所有点的距离,会导致计算量过大.另外,也可以对K邻近点进行加权计算,距离远的权重小,距离近的权重大,会提高分类的准确性.K近邻算法属于一种惰性学习方法,在预测时会效率低下.在空间复杂度上,该算法必须将所有的训练数据进行保存,还要为测试样本预留出另外的存储空间,如果样本数据过多,就会占用大量内存,使空间复杂度变高.