基于支持向量机回归的二次网供热负荷预测分析

王春青，王 凇，郑 杨，许添强，张 晗，李 超，王亦姝

1吉林建筑大学 市政与环境工程学院,长春 130118 2吉林省宇光热电有限公司,长春 130000

0 引言

目前,建筑能耗占我国总能源消耗的40 %,建筑能耗中又以供热制冷为主[1].随着国家对节能的重视以及计量供热的逐步推广,如何及时准确地调整实际供热负荷成为至关重要的问题.由于供热系统滞后性特点,采取调节措施之后需要一段时间才能起到控制作用,故有必要提前预测负荷变化趋势,以便提前应对,确保负荷供应与用户实际需求相匹配,避免造成能源浪费.

近年来,在负荷预测方面,国内常采用时间序列(Time series,缩写TS)、神经网络(Neural Networks,缩写NN)和支持向量机(Support vector machine,缩写SVM)等方法.邓盛川等[2]人通过自回归积分移动平均(Autoregressive integral moving average,缩写ARIMA)模型预测未来24 h的热负荷,得到预测最大误差为 3.14 %,但该模型对历史数据要求高,易受负荷变化影响,抗干扰能力较弱.王美萍等[3]人通过对供热负荷影响因素分析改善了小波神经网络,结果表明采用相关性较大的影响因素作为输入变量预测结果更接近实际值,然而该方法仍无法从根本上解决神经网络易陷于局部极小值,存在“过拟合”等问题.支持向量机回归(Support vector machine regression,缩写SVMR)是在SVM理论基础上推广的回归算法.该方法具有可靠的统计理论基础,能很好地适应高维度和小样本数据,使其用于供热负荷多因素非线性预测成为可能.

本文针对供热系统的影响因素及SVMR参数重要性,拟尝试按照交叉验证(Cross validation,缩写CV)与网格搜索(Grid search,缩写GS)和CV与遗传算法(Genetic algorithm,缩写GA)相结合的思想构建GS-KCV-SVMR模型和GA-KCV-SVMR模型,这样既能弥补以往参数选择时经验不足,又能利用GS和GA的全局搜索能力,克服训练时间过长等缺点.

1 SVMR算法介绍

1.1 SVMR理论

设数据训练样本为：

S={(x1,y1),(x2,y2),…,(xn,yn)},xi∈Rn,yi∈R

(1)

式中,xi为样本空间内的输入向量;yi为样本空间内的输出向量;n为高维空间向量的维数;i为样本数.

根据统计学理论在特征空间中构造最优回归函数:

yi=f(xi)=ωφ(xi)+b

(2)

式中,ω为权值向量;φ(xi)为映射函数;b为偏置量.

SVMR主要是通过非线性变换使下方目标函数最小化:

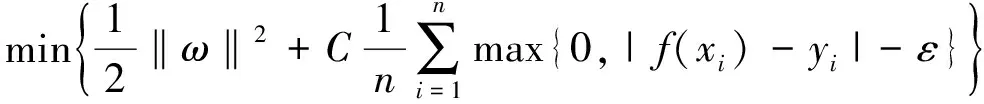
(3)

式中,C为惩罚参数;ω为上式的权值向量;ε为误差上限,即当预测值f(xi)与实际值yi的误差不超过给定误差精度ε时,说明回归函数与该点是拟合的.

引入拉格朗日乘子和对偶理论[4],最终数学描述如下:

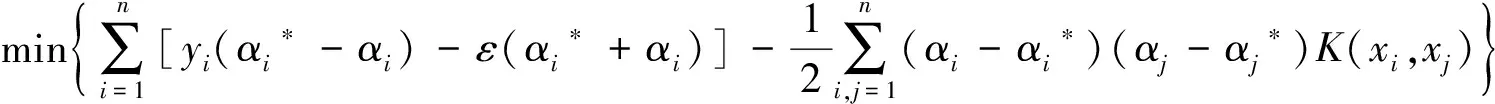
(4)

(5)

式(4),式(5)中,αi,αi*,αj,αj*为Lagrange乘子;ε为上式的误差上限;K(xi,xj)为内积核函数.核函数共有4种,由于径向基函数(Radial basis function,缩写RBF)应用范围广,且只有一个待优化参数γ,因此本文选用RBF为核函数,其表达式为:K(xi,xj)=exp(-γ‖xi-xj‖2)

1.2 支持向量回归参数

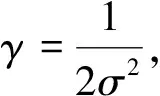
(1) 惩罚参数C表示预测值与实际值拟合偏差的惩罚程度,C越大越重视离群点,越趋向于训练集,拟合度较好,但泛化能力差;C越小,对离群点惩罚越小,容错能力增强,拟合度越差.

(2) 核函数参数γ反应训练数据特性,影响每个支持向量对应高斯作用范围,当γ过小即σ过大时,模型测试效果较差,训练效果较好,易出现“过拟合”现象;反之当γ过大即σ过小时,模型平滑效应太大,测试效果不好,训练误差也大,易出现“欠拟合”现象.

2 优化方法介绍

2.1 交叉验证

在参数寻优方法中,CV可适用于数据量不大的样本,能够有效避免“过拟合”与“欠拟合”[6].CV的基本思想是将原始数据划分成训练集和验证集,通过训练集建模,再用验证集测试.最常用的CV方法是K折交叉验证(K fold cross validation,缩写KCV),KCV将样本分割成K组,其中一组作为验证集,剩下K-1组作为训练集,交叉验证重复K次,最终得到K组模型,将每组模型测试结果相应评价指标的平均数作为KCV性能指标,该方法使所有数据都参与了验证,结果具有说服力.董美蓉等[7]人研究表明,当K=5时最低均方误差(Mean square error,缩写MSE)最小,故本文采用5折交叉验证,评价指标为均方误差MSEcv,即:

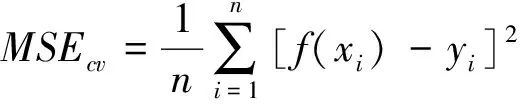
(6)

式中,yi为实际值;f(xi)为预测值.对预测模型而言,MSEcv值越小表示预测精度越高,反之预测精度越低.

2.2 网格搜索

GS是一种基于穷举法的最基本参数优化算法[8],其实质是将待优化参数赋值在一定范围的坐标系中,通过调整搜索范围和步长,每一点对应一组参数,GS-KCV-SVMR模型操作步骤如下:

(1) 确定参数C,γ的取值范围为C,γ∈[2-8,28],设置参数步长为1.

(2) 用KCV方法计算模型MSE值,并取平均值.若多组参数的评价指标相近,选取C最小的一组,若相同的C对应多个γ时,选择第一组为最佳参数对.这种方法既保证寻找出的参数是交叉验证下的全局最优解,又具有较好的拟合度和泛化能力.

(3) 不断重复步骤(2),直至找出最佳参数.具体流程如图1所示.

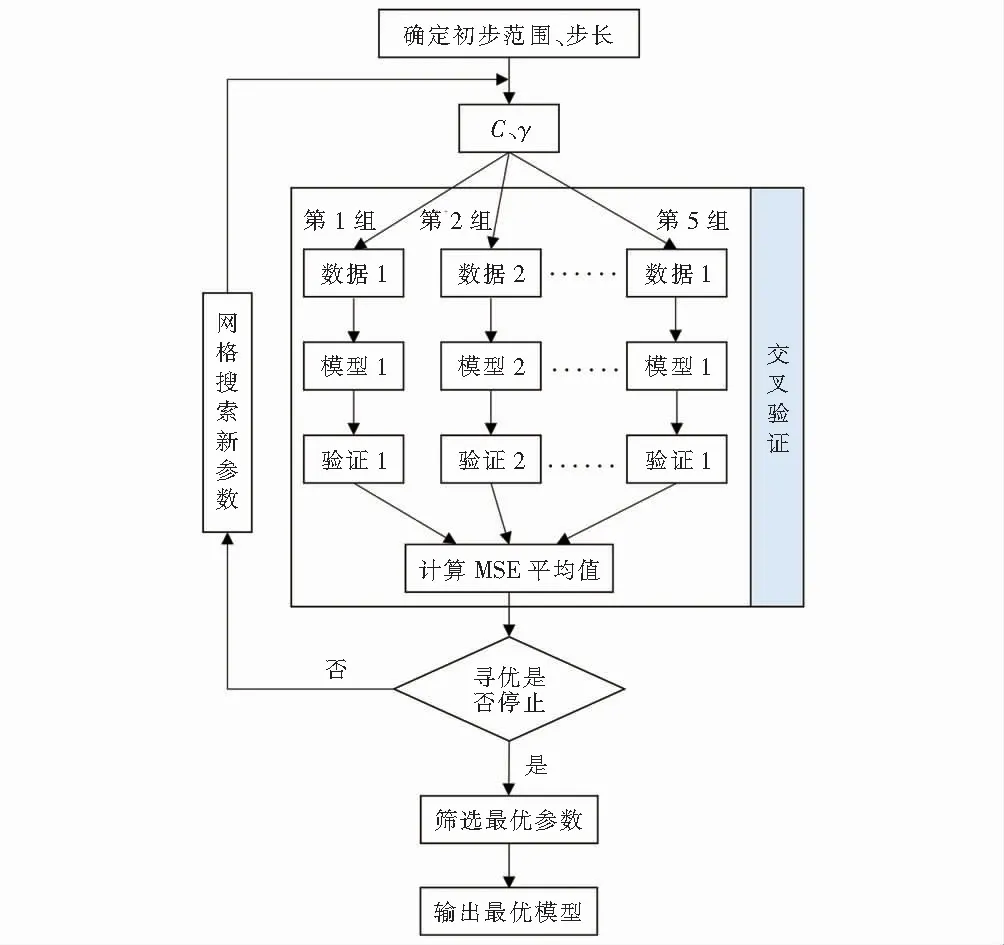
图1 GS-KCV-SVMR优化流程Fig.1 Optimization process of GS-KCV-SVMR

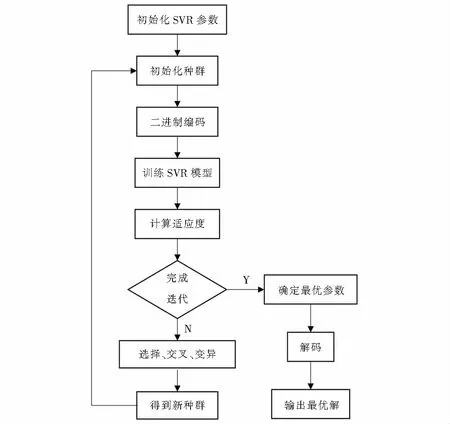
图2 GA-KCV-SVMR优化流程Fig.2 Optimization process of GA-KCV-SVMR

2.3 遗传算法

GA是Holland受达尔文进化论启发而提出的一种通过模拟自然进化过程搜索全局最优解的算法.该算法通过数学方法将优化目标参数组编码至生物染色体中,再选择适应度大的染色体复制、交叉、变异,直至适应度最佳的个体产生.由于其具有高效性、鲁棒性和全局最优性,已被广泛用于机器学习、图像处理和组合优化等领域.最主要的步骤是确定种群规模、编码方式、适应度函数及自身参数设定.GA优化SVMR参数流程如图2所示.

(1) 初始化SVMR参数,设置C,γ∈[2-8,28].

(2) 初始化种群及编码方式,设置种群规模为100,进化代数为30,采用由0,1组成的二进制编码.

(3) 计算适应度,本文采用的适应度为式(6)的均方误差.

(4) 个体选择,本文模拟转盘旋转过程,适应度越大即均方误差越小的个体被选中的概率越大.

(5) 交叉遗传,设置交叉概率为0.8.

(6) 变异操作,为增加种群多样性避免陷入局部最小值,随机选择发生变异基因,设置变异概率为0.2.

3 实验建模

3.1 数据来源

本文采集了长春市某住宅小区换热站低区数据,供热面积为168 616.7 m2,选取该区2020年10月23日～2021年4月2日供暖数据为样本,以天为单位,共计163组.采集数据包括室外环境温度、二次网供回水温度、二次网供回水压力和累计供热负荷等.

3.2 数据预处理

由于数据采集周期较长,易受人为操作,仪器故障等影响产生少量缺失值和异常值,SVMR模型对这些异常数据极为敏感,因此需在建模前对此类数据进行处理.本文结合插值法和多项式拟合法:对单一异常值,采用插值替换法即用其前后相邻数据的平均值替换原值;对局部异常值,采用多项式拟合平滑处理.考虑到各类数据的量级、单位不同,采用Mapminmax函数将所有数据归一化处理至[0,1]的概率分布中,变为无量纲表达式,从而简化计算.

3.3 输入变量选取

供热负荷预测的影响因素主要有室外天气因素和系统运行因素.室外因素有室外温度、风速风向和太阳辐射等,其中室外温度对热负荷的影响最大[9];系统运行因素有供回水温度和供回水压力等.张佼等[10]人研究表明,在输入变量中加入前3 d热负荷可更好地满足预测精度要求.故本文将室外温度、二次网供回水温度、二次网供回水压力、当日前3 d供热负荷作为初步输入变量,将当日后第7 d供热负荷即预测日负荷作为输出变量.然后通过皮尔逊相关系数法分析各输入变量与输出变量的相关性和显著性,分析结果见表1.

表1 各输入变量与预测日供热负荷相关性及显著性分析Table 1 Correlation and significance analysis of each input variable and the heating load on the predicted day

由表1可见,室外温度、供回水温度和当日前3 d负荷与预测日负荷均呈非常显著的强相关性,其中前3 d负荷距离当日时间越近相关性越强,满足时间序列中的热惰性滞后等特点;回水压力与预测日负荷呈不显著、弱相关,因此将该因素剔除,供水压力虽与预测日负荷呈非常显著、弱相关,但为保证模型准确度,不将此变量作为输入变量.

综上,本文以室外温度Tw、供水温度Tg、回水温度Th和当日前3 d的供热负荷Qt-1,Qt-2,Qt-3为输入变量,以预测日的供热负荷Qt+7为输出变量.预测模型的表达式为:

Qt+7=f(Tw,Tg,Th,Qt-1,Qt-2,Qt-3)

(7)

4 实验分析

4.1 评价指标

除上文中选用的MSE外,回归中还用平均绝对误差MAE(Mean absolute error,缩写MAE)和拟合优度R2作评价指标,具体公式如下:

(8)

(9)

4.2 结果分析

本文以采暖季2020年10月23日～2021年3月5日数据为训练样本,以2021年3月6日～2021年4月2日数据为测试样本.表2为不同优化模型下惩罚参数C和核函数参数γ选择结果,其中SVMR模型参数由人工试算得出,GA-KCV-SVMR的适应度曲线如图3所示,将两种方法优化后的参数输入SVMR模型并进行下一步预测.

表2 不同优化模型下参数选择结果Table 2 Parameter selection results under different optimization models

图3 GA-KCV-SVMR的适应度曲线Fig.3 The fitness curve of GA-KCV-SVMR

对样本数据进行训练.由SVMR模型、网格搜索优化模型和遗传算法优化模型得到供热负荷预测值、供热负荷实际值及它们之间的相对误差RE(Relative error,缩写RE),如图4～图5所示.

由图4可知,SVMR,GS-KCV-SVMR,GA-KCV-SVMR均相对成功地预测了未来7 d的负荷变化趋势,相比其他模型SVMR误差偏大,进一步说明了参数优化对负荷预测模型的影响.由图5可知,SVMR预测模型相对误差较大,最大值为±18 %,GS-KCV-SVMR,GA-KCV-SVMR相对误差较小,平均值分别为±10 %和±5 %.

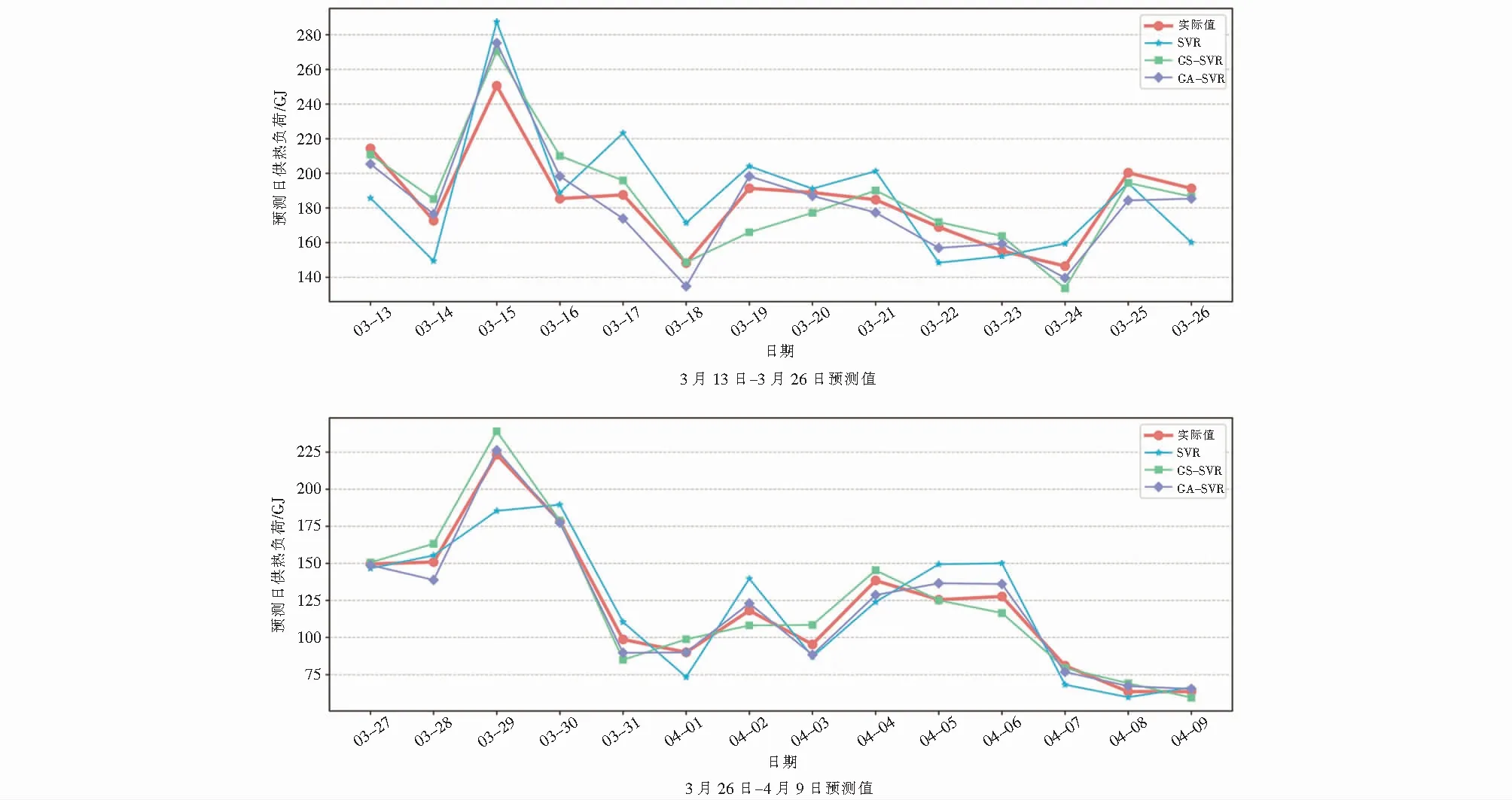
图4 不同预测模型3月13日～4月9日供热负荷预测曲线Fig.4 Heating load predicted curve of different predicting models from March 13 to April 9

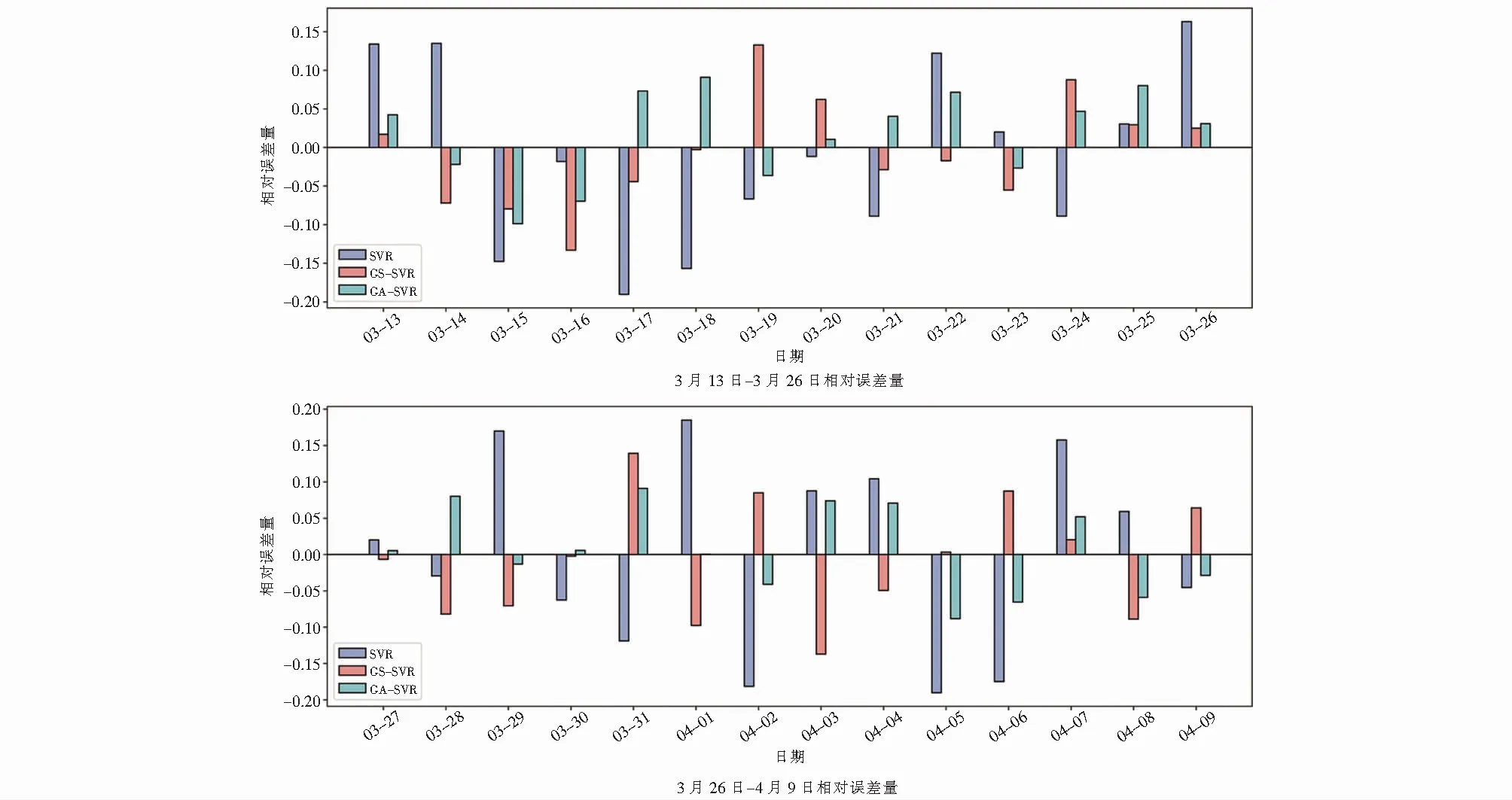
图5 不同预测模型3月13日～4月9日供热负荷预测相对误差Fig.5 The relative error of heating load predicted by different predicting models from March 13 to April 9

图6为不同预测模型评价指标对比,由图6可见,3种预测模型的拟合优度R2均超过了80 %,其中GA-KCV-SVMR分别比SVMR和GS-KCV-SVMR提高了11 %和13 %;GA-KCV-SVMR的MSE值为88.68,分别比SVMR和GS-KCV-SVMR减少了289.86和37.01;此外,SVMR的MAE值最大,分别比GS-KCV-SVMR和GA-KCV-SVMR增加了7.13和6.42.

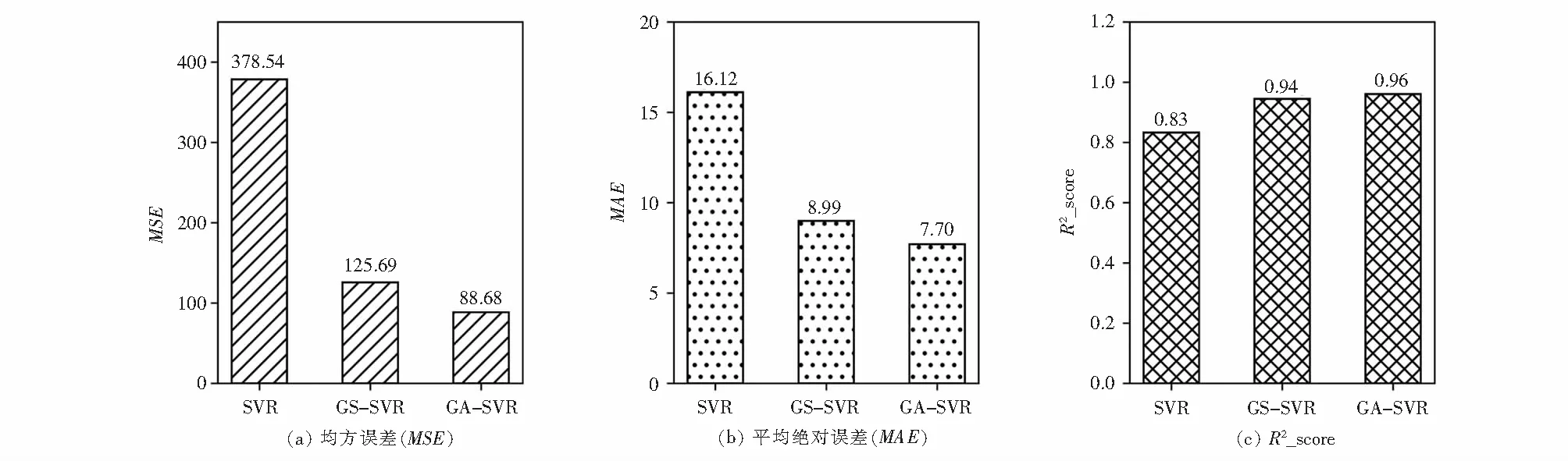
图6 不同预测模型评价指标对比Fig.6 Comparison of evaluation indexes of different prediction models

5 结论

(1) 本文以室外温度和系统运行影响因素为输入变量,建立了SVMR供热负荷预测模型,并通过网格搜索和遗传算法优化模型参数,克服了传统SVMR模型参数选择的盲目性和随意性,按照交叉验证思想,有效避免“过拟合”与“欠拟合”,为预测模型建模提供了参考.

(2) 仿真结果表明,经遗传算法优化,SVMR模型最大相对误差RE为±8 %、均方误差MSE为88.68、拟合优度R2为96 %,优势较为明显,在热源分配和运行调度方面有一定实用价值.