基于归一化磁源强度垂向差分的磁源参数快速估计方法

黄远生，王彦国，罗潇

(1.东华理工大学 地球物理与测控技术学院,江西 南昌 330013；2.海南水文地质工程地质勘察院，海南 海口 571100；3.核工业230研究所,湖南 长沙 410011)

0 引言

磁异常快速反演一直是磁法数据处理与解释的研究重点与热点，该类方法能够在无先验信息约束下快速获取场源的位置与几何参数。目前较为常用的快速反演方法有欧拉反褶积法、解析信号法、tilt-depth法等。欧拉反褶积是Peters[1]提出的，Thompson[2]推导了二维欧拉反褶积，Reid 等[3]将其推广至三维。张量欧拉反褶积[4]扩展了欧拉方程个数，提高了反演解收敛性；Huang 等[5]证明了位场解析信号同样满足欧拉齐次方程；AN-EUL 法[6]能够快速估算场源深度与构造指数；Tilt-Euler 法[7]无需已知场源构造指数，避免了因构造指数选取不当导致反演解发散的问题；张量局部波数的欧拉反褶积法[8]进一步扩展了方程组个数，获得了良好的应用效果。不过欧拉反褶积及其改进方法的反演解中存在大量的虚假解，需要建立有效的筛选机制，另外背景场、噪声干扰及窗口大小选择也会对反演结果产生一定影响。二维磁解析信号振幅不受磁化方向影响[9]，Macleod[10]推导出了二维磁解析信号振幅的通用表达式；Salem 等[11]在解析信号及其水平总梯度基础上采用线性最小二乘法计算磁源深度及构造指数；Salem 等[12]又根据解析信号及磁异常垂向导数解析信号关系进行磁源参数估计；Ma 和Du[13]在解析信号振幅的解析信号与解析信号比值基础上提出了改进解析信号来实现单一场源深度及构造指数的估算；Cooper[14-15]同样采用不同阶次解析信号来估计岩脉及台阶的深度；Cooper 和Whitehead[16]利用不同阶次解析信号比值进行场源深度估算，不过改进方法不需要已知构造指数；Cooper[17]又采用了解析信号对数实现磁源深度估计工作。Wang等[18]采用解析信号及其倒数进行磁源参数反演计算，对深部场源反演效果较好。但三维解析信号在一定程度上受磁化角度影响，在三维磁异常反演中使用较小。Tilt-depth 法可用于快速估算场源上顶深度，该方法是由Salem 等[19]在Tilt 梯度及磁场通用梯度公式进行理论推导而来；Fairhead 等[20]提出了基于化极与化赤相结合的tilt-depth 法，还可以实现场源磁化率估计；张恒磊等[21]提出了基于二阶导数的磁源边界与顶部深度快速反演方法，有效地消除了区域场对反演结果的影响；Wang 等[22]提出了改进tilt-depth 法来估计磁源的上顶与下底深度，并采用多特征点联合计算来提高反演解的可靠性；Cooper[23]在Hilbert 变换基础上推导出了岩脉模型的垂直磁化磁位的tilt-depth 公式，提高了方法实用性及稳定性；曹伟平等[24]对tilt-depth 法进行了深入研究，指出了该方法并不适用于埋深大、水平尺度小的磁源深度反演计算。由于tilt-depth 法及改进算法均需要在化极或化赤基础上完成计算，因此并不能直接用于斜磁化磁源深度的估算。

归一化磁源强度是在磁梯度张量特征值基础上提出的，该方法不(少)受磁化方向影响，是三维磁异常解释的常用工具。Wilson[25]首先给出了磁偶极子下归一化磁源强度的表达式，Beiki等[26]给出了归一化磁源强度的通用表达形式，建立了归一化磁源强度与场源位置、构造指数的关系，同时结合欧拉反褶积实现了三维磁源的位置及构造指数反演；Pikington 和Beiki[27]在归一化磁源强度基础上实现了剩磁情况下的磁源空间位置及磁化率反演；Guo等[28]将归一化磁源强度与相关成像结合来反映地下磁性体的三维空间展布状态；饶椿锋等[29]将归一化磁源强度与正则化共轭梯度法结合来反演磁源的磁化率。本文在归一化磁源强度垂向差分基础上，提出了一种场源快速反演方法，并进行了模型分析与实例应用。

1 基本原理

对于体积为V，磁化强度为M的磁性体，其磁位U的表达式[30]为：

(1)

式中：|r-r0|是观测点到场源点的距离。

磁梯度张量[31]可以表示为：

(2)

式中：μ0为真空磁导率；Bx、By、Bz是磁场B的x、y、z这3个方向分量。对梯度张量Γ进行对角化处理，得：

(3)

式中：l1、l2和l3为Γ的特征向量；λ1、λ2、λ3为对应的特征值。Wilson[25]给出磁偶极子的归一化磁源强度μ的定义，并推导出梯度张量特征值表达式：

(4)

Beiki等[26]给出了归一化磁源强度的统一表达式：

(5)

式中：α是与磁化强度有关的物理量；(x,y,z)和(x0,y0,z0)分别是观测点与场源点坐标；N为构造指数，与磁源几何形状有关，当N=0，1，2，3时，分别对应台阶、岩脉、圆柱体及球体。

当Δz→0，对于两个不同高度z1,z2，有：

(6)

(7)

分别将式(6)、(7)对式(5)做比值，得：

(8)

(9)

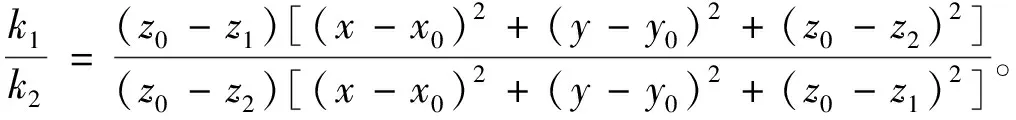
(10)

当x→x0,y→y0时：

(11)

则磁源深度z0可表示为：

(12)

将z0表达式带入式(8)或(9)，可求得构造指数N：

(13)

显然，估计场源深度z0和构造指数N，需要事先给定场源的水平位置(x0,y0)，Δz取值以及z1、z2的大小。由于归一化磁源强度的垂向差分极大值对应着场源水平位置，因此场源的水平坐标(x0,y0)则看作是归一化磁源强度垂向差分(Δμ1)极大值位置；Δz不易过大，一般取0.05～0.2倍点距，否则式(6)、(7)不满足，反演误差较大，本文取0.1倍点距；z1、z2的大小需要根据磁异常的信噪比决定，当噪声含量较小时，z1、z2可较小。另外，当异常较为复杂时，|z2-z1|≤5Δx且z1和z2两者取值均不易过大，以避免延拓过大导致不同场源异常相互影响而使反演结果误差增大。需要指出的是，由于反演结果仅在场源位置(x0,y0)有效，而远离场源位置的反演结果完全无参考意义，因此在反演图中可仅保留归一化磁源强度垂向差分极大值附近的结果。

2 模型试验

2.1 单一球体

为了验证本文算法的正确性，设计了一个单一球体模型，模型参数为：半径为0.5 km，埋深为1 km，磁化倾角和磁化偏角均为60°，磁化强度为1 A/m。图1a为单一球体模型的磁异常，图1b与1c是归一化磁源强度及其垂向差分结果，可以看出，归一化磁源强度(图1b)极大值与球体质心相吻合，等值线成同心圆分布，异常特征完全不受磁化方向影响，而归一化磁源强度垂向差分(图1c)相对于归一化磁源强度，异常更加汇聚。图1d和1e是本文算法获得的磁源深度及构造指数，可以看出，深度及构造指数反演图均在球体质心位置存在极小值，极小值分别为1.02 km及3.1，均与理论值1 km和3非常接近，这反映了本文算法的正确性。

图1 单一球体磁异常反演结果(z1=0 km, z2=0.2 km)

2.2 组合模型

为了验证本文方法对复杂情况的处理能力，设计了一个球体、长方体、薄板、岩脉构成的组合模型，各个模型体参数见表1。图2是组合模型产生的磁异常，可以看出，归一化磁源强度(图3a)能够利用极大值很好地反映出球体质心、棱柱体及薄板边界和岩脉位置；归一化磁源强度垂向差分(图3b)对各模型体刻画的更加精细，异常分辨率获得了明显的提高。图3c、d是本文方法反演得到的场源埋深及构造指数。在球体①质心的反演深度为1.52 km，构造指数反演值为3.0；棱柱体②边界位置上的深度反演解在0.5～0.7 km之间，平均值为0.61 km，构造指数反演解集中在0.2～0.5之间，平均值为0.34；薄板体③边界上的深度反演值在0.47～0.65 km之间，平均值为0.51 km，构造指数在0.55～1之间，平均值为0.77；岩脉④的反演深度集中在1.0～1.15 km，平均值为1.08 km，构造指数在1.05～1.25之间，平均值为1.16。从反演结果可以看出，由于异常叠加影响，反演结果均与理论值存在偏差，但较接近于理论值，且深度反演的平均相对误差仅为8.3%，反演结果仍较可靠。

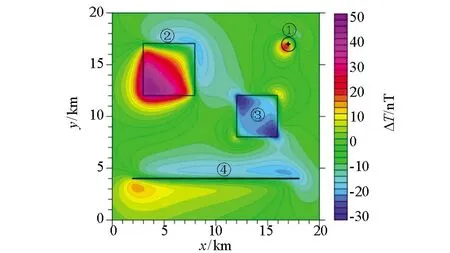
图2 组合模型正演磁异常

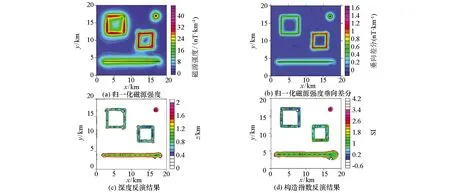
图3 组合模型磁异常的反演结果(延拓点距z1=0 km，z2=-0.2 km)

表1 模型体参数

为了了解噪声干扰对本文算法的影响情况，对叠加异常(图2)添加了1%的随机噪声，见图4。图5、6和7分别是选取了不同延拓高度的归一化磁源强度及其垂向差分，和深度及构造指数反演结果。

图4 含1%随机噪声的组合模型磁异常

图5 含噪组合模型磁异常的反演结果(z1=0 km, z2=-0.2 km)

从图5可以看出，未延拓情况下的归一化磁源强度(图5a)虽然存在明显的异常波动，但仍可以清晰地展示出所有模型体的水平位置；垂向差分(图5b)受噪声干扰影响明显，仅能识别出薄板的边界位置，对其他模型反映极为模糊；反演得到的深度(图5c)和构造指数(图5d)也仅在薄板边界上有异常展示，但反演结果波动大，与真值也存在较大偏差。

从图6中可以看出，向上延拓3倍点距的归一化磁源强度(图6a)异常较为圆滑，垂向差分(图6b)的稳定性获得较大程度上的提升，能够较好地展示所有模型体的水平位置。图6c和6d是场源深度与构造指数反演结果，表2也给出了无噪声和含噪声不同延拓高度时的反演结果。在该延拓情况下，球体质心埋深反演结果为1.46 km，构造指数为2.88；棱柱体深度反演解在0.4～1.1 km之间，均值为0.74 km，构造指数反演解在0～1.2之间，均值为0.63；薄板的深度反演值在0.4～0.8 km之间，均值为0.51 km，构造指数反演值在0.4～1.5之间，均值为0.76；岩脉深度反演解在0.8～1.4 km之间，均值为1.09 km，构造指数反演值在0.7～1.6之间，均值为1.18。对比无噪声时的反演结果可知，所有模型体的深度反演精度都有所降低，尤其棱柱体深度的相对误差高达48%，不过其他模型体的深度反演误差均小于10%，且深度反演的平均相对误差为 15.4%，因此，认为反演结果仍具有一定的可靠性。

表2 无噪及含噪组合磁异常不同高度上的反演结果

图6 含噪组合模型磁异常的反演结果(z1=-0.3 km, z2=-0.5 km)

从图7可以看出，向上延拓5倍点距的归一化磁源强度(图7a)及其垂向差分(图7b)异常更加圆滑。图7c和7d是场源深度与构造指数反演结果，球体质心埋深反演结果为1.54 km，构造指数为 3.05；棱柱体深度反演解在0.5～1.4 km之间，均值为0.94 km，构造指数反演解在0.3～1.5之间，均值为0.80；薄板的深度反演值在0.3～0.7 km之间，均值为0.45 km，构造指数反演值在0.3～1之间，均值为0.61；岩脉深度反演解在0.8～1.3 km之间，均值为1.09 km，构造指数反演值在0.5～1.5之间，均值为1.18。对比z1=-0.3 km，z2=-0.5 km时的反演结果可知，几乎所有的模型体深度反演精度进一步下降，尤其棱柱体深度的相对误差由48%升至88%，深度反演的平均相对误差为27.4%。由此可见，延拓高度较大时，虽然归一化磁源强度及其垂向差分异常更加光滑，但是反演精度却有所下降，主要在于延拓高度较大时，不同场源的异常相互影响更严重。

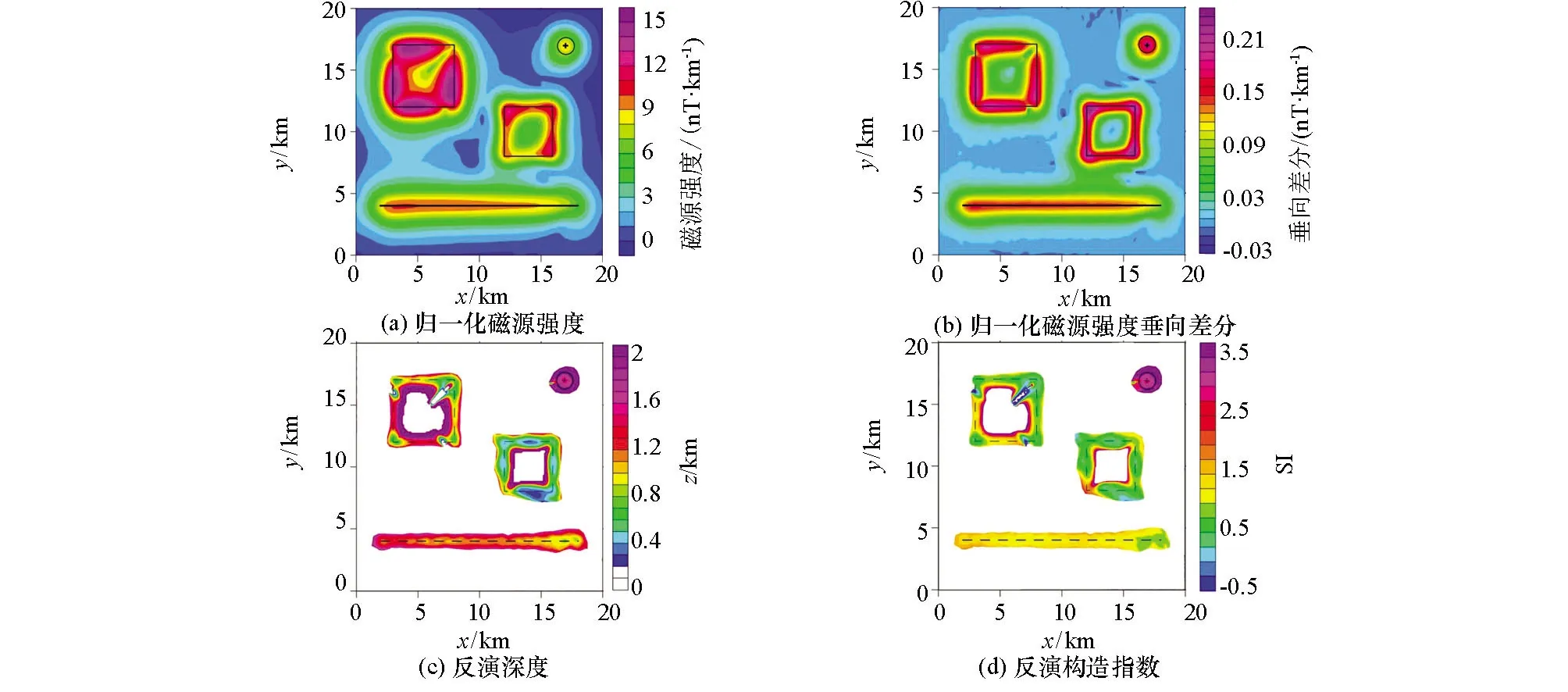
图7 含噪组合模型磁异常的反演结果(z1=-0.5 km, z2=-0.7 km)

3 实例应用

为了验证本文方法的实用性，选取了内蒙古M地区的地面磁异常进行实验。图8是研究区的地质图，可以看出，该地区地表分布的是沉积岩和火山岩，具有一定磁性的晚奥陶世闪长岩主要分布在中西部(东2～10 km，北3～6 km)、中部(东23～28 km，北3～7 km)及中北部(东29～35 km，北5～9 km)3块，其他类型岩石基本无磁性。图9a是研究区地面磁异常，测网密度为250 m(东)×50 m(北)，图中可以看出，测区中部存在一条近EW走向转EN走向的条带状磁异常，在测区东部还存在一个明显的高磁异常圈闭区，地表出露的闪长岩上方基本都是以高磁异常显示。图9b是z1=-0.5 km时的归一化磁源强度，可以看出，归一化磁源强度异常形态更加简洁，高异常分布区与磁异常中的高异常区基本吻合，其主要原因是该地区处于高纬度地区，高磁异常基本与磁性体位置相对应。图9c是z1=-0.5 km时的归一化磁源强度垂向差分结果，可以看出，该图与归一化磁源强度基本一致，不过异常更加收敛，另外东侧的高异常分布区较模糊，这可能反映了该区磁源埋深较大。图9d和9e是利用本文算法得到的磁源深度z0及构造指数N分布图，可以看出，地表出露的闪长岩分布区，反演深度基本都是0 km，构造指数多分布在1附近，即可当作岩脉看待；中部条带状磁异常上的深度反演结果基本都在0～1 km之间，即隐伏的高磁性体(推测为闪长岩)埋深相对较浅，构造指数反演结果则由西往东有逐步增加的趋势，基本从1变化到3，这可能是西侧磁性体宽度小而东侧偏大，或东侧磁源从浅往深规模逐渐扩大所致；东部高磁异常圈闭区的深度反演结果表明该磁性体从西南往东北埋深逐渐减小，而构造指数从西南往东北同样逐渐减小，这可能反映了磁性体形态上从穹窿状往脉状的一种转变。

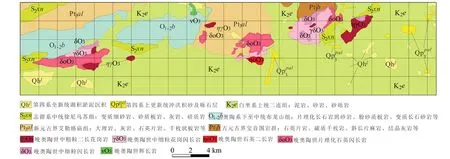
图8 内蒙古M区地质

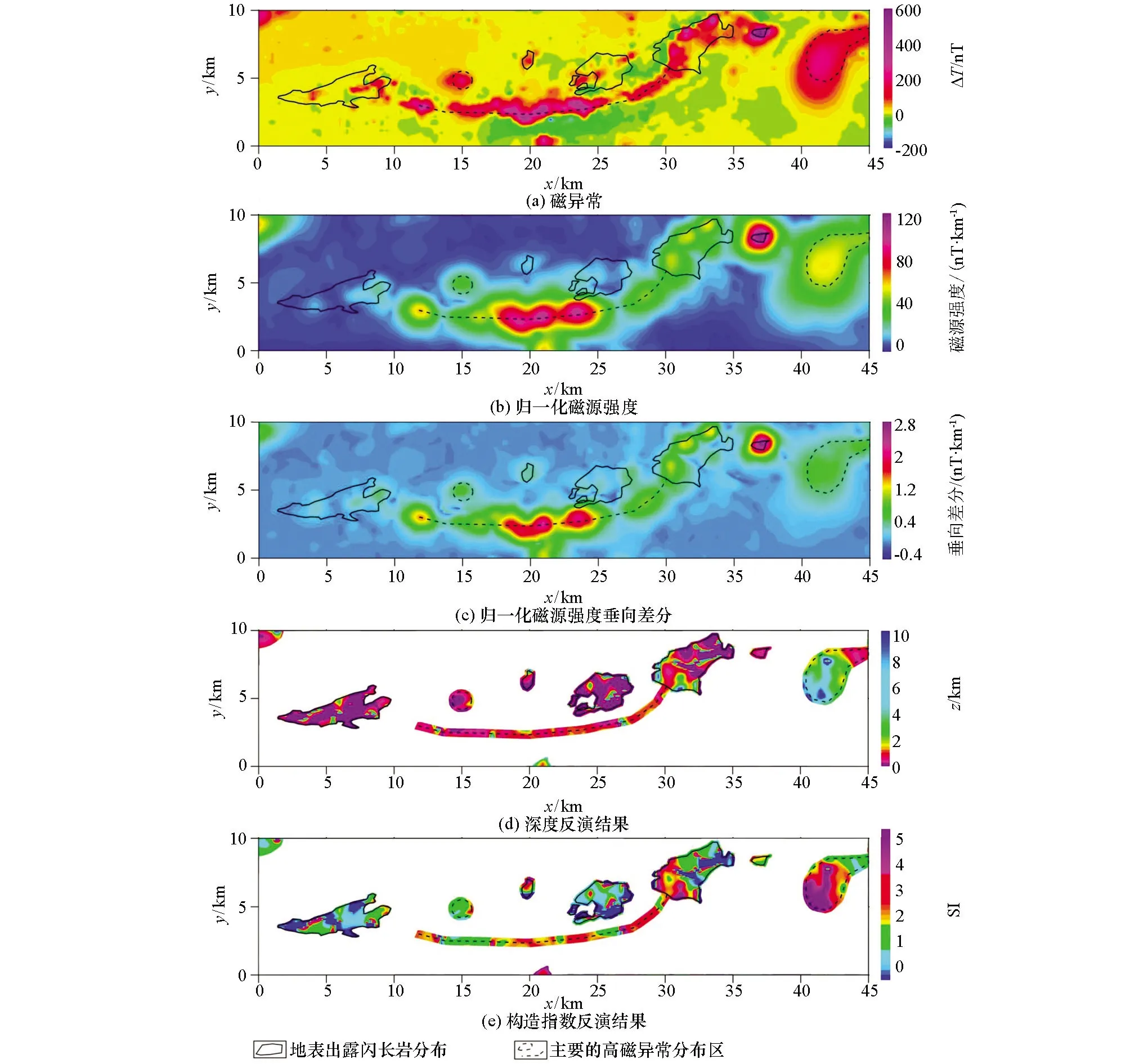
图9 内蒙古M地区磁数据处理(z1=-0.5 km，z2=-0.75 km)

4 结论

归一化磁源强度是三维磁数据解释常用的方法，主要在于该方法不(少)受磁化方向影响。本文在归一化磁源强度基础上，进行了垂向差分计算，并根据不同高度上差分关系，提出了一种磁源参数快速反演方法。模型分析表明了归一化磁源强度垂向差分提高了原方法的分辨率，能更清晰地展示异常间关系；基于归一化磁源强度垂向差分的反演方法能够有效地反演出磁源的深度与构造指数。在内蒙古M区实例应用中，归一化磁源强度垂向差分识别出了一条近东西走向的高磁异常带和一个范围较大的高磁异常圈闭区，反演算法计算结果表明了东西走向的高磁异常带对应的磁源埋深较浅，形状偏向于岩脉，而高磁异常圈闭区对应的磁源埋深较大。本文提出的磁异常快速反演方法能够很好地估计场源位置信息与几何形状信息，方法原理简单，易于实现，为三维斜磁化磁异常解释提供了新的研究思路。