一种实测重力异常区域场的消除方法

2021-12-23王正科卢琳刘花婷

物探与化探 2021年6期

王正科，卢琳，刘花婷

(陕西地矿第二综合物探大队有限公司,陕西西安 710016)

0 引言

实测重力异常包含了从地表(观测面)到深部所有密度不均匀引起的重力效应，即是观测面以下所有不均匀密度体的叠加异常。在解译某个(类)目标地质体所产生的重力异常时，必须从实测重力异常中分离出单纯由该地质体引起的异常，再对这个异常进行反演获取目标地质体形体、规模等参数。然而，要把单个地质体所引起的重力异常从实测重力异常中分离出来还是非常困难的，因此实测重力异常的分离就是地质解释工作中的重中之重。

对于实测重力异常的复杂性[1]，划分区域(场)异常和局部异常的方法多种多样，诸如：小波多尺度分析法、补偿圆滑滤波法、正则化位场分离法、圆周平均法、滑动窗口平均法、插值切割法、滑动趋势分析法等。这些方法均是对已经给定的场进行分离，每一种方法都有其局限性和不足之处，其中滑动窗口平均法的不足之处为：① 正方形窗口过大达不到分离局部异常的目的；过小则区域场中保留许多局部异常；② “虚假异常”是方法的固有原因，不可避免，使用此方法需要选择不同参数而做出多种相关图件，并需要在解释中相互参照对比和补充。

滑动趋势分析法的不足之处则是多项式的次数选择问题，次数高则会导致拟合异常的震荡效应加剧，叠加的局部异常趋势不明显。一般选取“1、2、3”次多项式，按照“最小二乘法”进行回归分析，取“最佳”(窗口多项式拟合值与节点异常值之差值最小)作为网格节点的局部异常值。

如此诸多分离重力异常的方法使用的网格化数据大多是仅考虑平面位置和异常的关系，而没有考虑高程和异常的关系，这样是不完整的。因为实测重力异常的观测面(地表)是不平整的，呈现的重力异常图与地形高程的关系比较密切，即是重力异常与地形海拔高程呈现“正”比或“负”(反)比关系。

关于实测重力异常与高程关系，彭聪等[2]、孟昭秦等[3]通过对重力测量成果进行了统计分析，提出按照矩形小区域分割法对布格重力异常与地形高程之间的关系，用异常与高程之一次、二次回归方程分离重力异常的方法，并分析了布格异常与高程呈现负相关的主要因素。龚育龄[4]列举不同类型的地形特征，对大地水准面上的重力值与地形高程进行相关分析，在区域性小比例尺及均衡补偿基本完善的前提条件下，两者有极好的线性相关关系，利用相关分析处理重力叠加场可以收到好的效果。陈超等[5]对重力测量经过外部改正所得的所谓“山形异常”的原因进行分析探讨，提出用滑动窗口调整中间层密度的方法和以相对海拔高差校正的方法来避免“山形”虚假异常的产生。

前人提到的用数理统计回归方法分离重力异常和消除虚假异常的方法，多数是在将所要研究的工作区用一定范围的窗口进行分区划分，用平均值或随机均匀地选取一定数量的测点来进行统计分析，取得了非常好的效果。

1 方法原理

本文所述“回归剩余异常法”主要是针对离散观测点单点来进行回归分析[6]的，并且不受工作区域大小、工作区包含测点的多少限制的一种重力异常分离方法，并且对实测重力异常的分离不仅仅局限于布格重力异常(简称“布格”)，同时对自由空间重力异常(简称“自空”)和未做地形改正校正的简单布格重力异常(简称“简布格”)也采用同样的方法进行分离，做到多参数对比分析，相互借鉴，相互补充。

由于是用单点异常值来进行分析，因此也就不受工作比例尺的约束，再加上运用多种异常值来进行相互补充，得到的结果更接近于实际情形。

1.1 方法原理

回归剩余异常：

gs=g-gj，

(1)

回归异常(图1)：

gj=k·hj+c，

(2)

其中，一次项系数k：

(3)

常数项(截距)c：

(4)

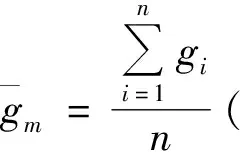
注：式(1)～(4)中的g可以用“自空”、“简布格”和“布格”的任意一项。

对于重力异常来说，重力观测结果经过各项改正后所得异常与测点高程(h)的一阶次成比例对比分析。在分析过程中，将这些(类)异常与高程进行线性回归统计是较为合理的，如果采用二阶次[7]及以上的曲面方程，则会导致局部场和区域场均出现局部“振荡跳跃”现象，与重力场波长长的特点是相悖的(图1)。

图1 回归分析方法示意

再者所用的异常值除“简布格”外，其他用来进行回归计算的参数种类与前人[8]所述基本一致的，只是各项改正中的的参数项有所不同，即：① 高度改正中增加了与纬度有关的变化项和高度改正补偿项，而非仅用与高度有关的一次项；② 中间层改正中采用半径为20 km圆形平板公式，而非单纯的平板公式。

1.2 引入关系项

比较两种数值之间的关系时，常用两者之间的相关系数[9](无量纲)来表示它们之间的密切程度，对于一个工作区来说，由于待比较数值之间呈现离散状分布，一般采用小区域内两者数值之间的相关系数进行比较，也就是用一个固定的窗口进行滑动计算，得到与待比较数值范围相同的一组关系数据，再进行图示关系分析。两种数值的相关系数计算公式如下：

(5)

式中：a1、a2为窗口内两类数值；m为窗口内单类数值的个数(两类数值个数相同)。

对于相关系数，一般认为其值|v|≤1.0。多数情况下在讨论相关系数时，当|v|≥0.8时为强相关；当0.3≤|v|<0.8时为弱相关；当|v|<0.3时则为不相关。

2 实例

2.1 A区重力测量

从A区(工作比例尺≤1∶200 000)重力测量成果分析对比看(图2)，由于研究区地形条件复杂，所得布格异常[10]较为简单，布格异常呈现“地势高、场值低”的近似反比例关系。布格异常相与高程回归分析得到的剩余异常的形态与地形接近于正比例关系，更凸显工作区域的异常特征。

对比两者(图2a、b)用“滑动平均场法”(两项数据处理的半边长是相同的，仅是为说明问题而非正常的地质解释。下同)得到的剩余异常(图2d、e)可以看出如下区别：① 两者的“零”值线圈定范围变化不大；② 回归剩余异常之剩余异常的幅值变化更为明显，“局部”异常之延伸追索更为直观，(同性状)条带状分布特征更为突出；③ 反观相关系数(图2f)，两者之“滑动平均场法”剩余异常的强相关性更为明显。与地形等高线对比，“正”相关对应地形“低”，“负”(反)相关对应地形“高”。

2.2 B区重力测量

从B区(工作比例尺1∶50 000～1∶200 000)重力测量成果分析对比看(图3)，“布格”异常(图3a)与地形等高线(图3c)相似很强。去掉与高程有关之项(即布格异常与高程回归分析结果)后，得到的图形(图3b)规律性(异常展布特征)也很强。

再看两者(图3a、b)之“滑动平均场法”剩余异常(图3d、e)之间的特性：① “布格”剩余异常之局部异常较为“凌乱”，而“布格”回归剩余异常之剩余异常的规律性较强，局部异常的“追索”和“连通”效应较为明显，展布规律与“布格”剩余异常存在“差异”；② 由于“布格”异常含有与测点高程有关的区域项，其相对变化较大，则剩余异常的“幅值”较大而连续性较差。反观“布格”回归剩余异常之剩余异常的“幅值”较小而连续性较好；③ 从相关系数图2f看，虽然图3d、e所反映的结果不尽相同，可是能够反映出两者之间有一定的连续性，且“正”相关大多与局部地形高或过渡带有关，“负”(反)相关多于局部地形低有关。

2.3 小比例尺与中比例尺重力测量对比分析

众所周知，对于开展不同比例尺重力测量工作(包括磁法测量工作和其他诸如电法勘探、地震勘探等)时，为了不同的工作目的，工作部署和布置是有区别的，特别是开展大比例尺工作时，对于探测目标的不同，多数情况下还要采用不同工作比例尺进行组合，即目标测区需要开展大(或超大)比例尺工作，周边区域(非探测区)采用中比例尺工作进行填补(此区域采集的资料主要是用于扩大数据处理的应用而减少目标测区的边部损失)。

这里就图2和图3进行对比分析，说说两者的普遍性和特殊性。

首先是普遍性：① 对于重力测量来说，通过高程与相应的“简布格”、“自空”和“布格”进行相关分析，用单个测区的所有数据进行统一分析时，其分析结果是独立不变的，即相关系数、参数(“简布格”、“自空”和“布格”)与高程之间的关系方程也是各自独立不变的；② 通过分析所得到的回归剩余异常的规律性更明显，即相应的重力高和重力低更突出；③ 均是浅部小尺度目标体的反映。

其次是特殊性：① 小比例尺所得回归剩余异常与常规分析之剩余异常差异不大(范围、延伸近似一致，只是幅值变化较大)，而中比例尺所得回归剩余异常则与常规方法存在差异，其局部异常的延伸、规模和幅值有时会截然不同；② 小比例尺之测点的间隔较大，统计分析所用到的测点数少及其控制范围也较大，所反映的是较大尺度的地质体。中比例尺之数据点间隔较小，统计分析所控制的范围也较小，分析结果所反映的地质体的尺度也较小；③ 同样，由于中比例尺之数据点密集，所反映的细节较为丰富(图3中e)，相对于小尺度的地质体的延伸可能与大尺度地质体不一致。

这样即可得到，不论哪种工作比例尺所得到的重力测量成果，通过多点线性回归统计法所得到的回归剩余异常均能够反映出相应比例尺工作的成果。

通过与常用的方法进行比较(图2和图3中的d、e)，不仅局部异常的展布范围相同或相似，而且，众多的局部异常还表现为幅值加大，“连通”、“延伸”和平面“展布”也更加明显，“分级”的效果会更加明确，仔细分析所得结果可能还会有所新的发现(图3中的d、e)。

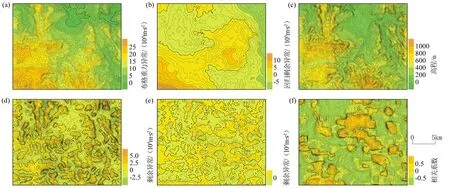
a—“布格”异常；b—“布格”回归剩余异常；c—地形等高线; d—(a)的“平均场”剩余异常；e—(b)的“平均场”剩余异常；f—(d)和(e)的相关系数

3 讨论

3.1 “简布格”、“自空”与“布格”三者回归剩余异常之间关系

图4为小比例尺重力测量工作之“简布格”、“自空”和“布格”之回归剩余异常对比。从图可以看出，“简布格”与“自空”之回归剩余异常相似程度较高，相关系数接近于1.0(|v|>0.999 5)，两者表现为强正相关(即为“同高”或“同低”)，与两者的数据处理过程是密切相关的。而“自空”与“布格”、“简布格”与“布格”之回归剩余异常虽然也呈现强“正”相关性(图4e和f)，但弱相关区域明显加大。

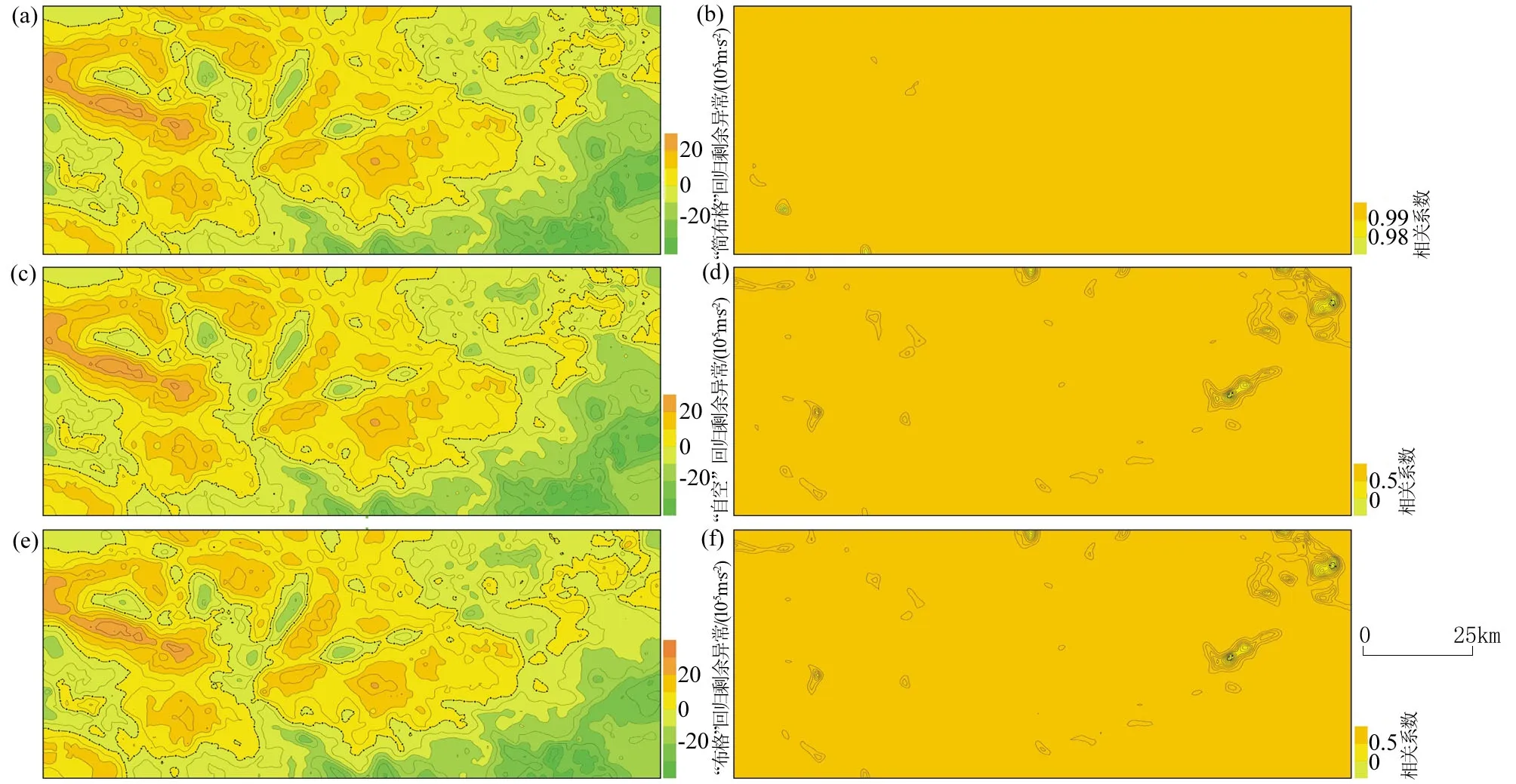
a—“简布格”回归剩余异常；b—“自空”回归剩余异常；c—“布格”回归剩余异常; d—(a)与(b)相关系数；e—(b)与(c)相关系数；f—(a)与(c)相关系数

图5为中比例尺重力测量工作之“简布格”、“自空”和“布格”之回归剩余异常对比。由于工作比例尺的不同，工作成果显示的效果也不同(大比例尺工作的测点较为密集，即测点之间的间隔距离较小)，所可以显示的成果有所变化。这里就图形显示的规律加以描述(不涉及地质解释)。

从图5可以看出，“简布格”与“自空”回归剩余异常在工作区域内的大部分区域(超过90%以上)呈现“正”相关，“弱”相关与“负”(反)相关展布区域极小；“自空”和“布格”、“简布格”与“布格”之回归剩余异常之强“正”相关区域展布较大(60%～80%左右)，“弱”相关与“负”(反)相关区域明显加大，推测与局部地形的变化关系较大。

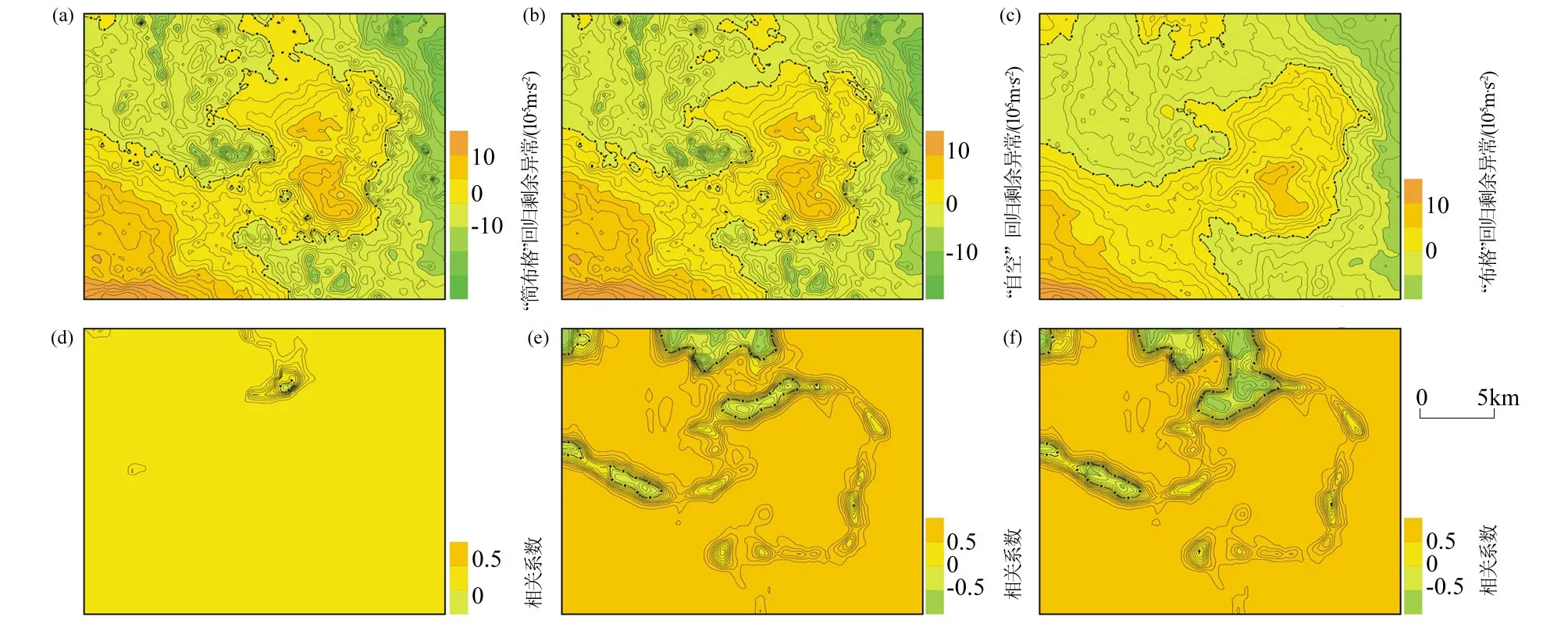
a—“简布格”回归剩余异常；b—“自空”回归剩余异常；c—“布格”回归剩余异常; d—(a)与(b)相关系数；e—(b)与(c)相关系数；f—(a)与(c)相关系数

3.2 关于地形改正问题

通过图4和5的对比分析，再结合重力测量原始资料的整理过程，不难发现：由于“自空”异常是在将实际观测所获得的重力原始成果(三维位置、重力值等)，经过正常场改正、高度改正得到的，其中仅涉及到测点的位置参数(平面位置和海拔高程)。而“简布格”异常是在“自空”异常的基础上进行了中间层改正。此两者按照同样的规律(“自空”和高程、“简布格”与高程)进行线性统计回归分析，所得回归剩余异常之数值和图形展布形式几乎是一模一样。

而“简布格”与“布格”则有所不同，即“简布格”是没有考虑地形影响的布格异常，“布格”则是考虑了测点周围之地形影响所得到的布格异常，两者之差就是一个地形改正。

然而，将加入地形影响后的布格异常按照本文提出的方法进行回归分析，两者之间的差异还较大(图4和图5中的a、c)，不仅幅值差异大，而且异常的展布方向也较大，特殊情况可能还会面目全非。

重力测量结果受到地形影响这是没有疑问的，从教科书和专业技术书籍中都可以找到答案。计算方法的数理推导过程也非常严谨和缜密，并且设计的理论模型也都可以得到很好的效果，所有这些理论同样得到了大家的公认。本文认为存在两方面的原因：

第一，就是关于地形改正之地形模型的问题。从重力测量的基本点出发，地形对重力测量的影响是在重力观测时刻测点周围地形的特征所产生的，观测时刻的地形影响是通过理论计算得到的。由于要用到计算机程序，那就要按照一定的假设条件进行过程分解和逐项计算，其中最主要的是地形模型的规则化(即按照一定的节点间距分解地形模型)，而后采用模型系数法进行地形改正值的计算。可是对于所用到的地形模型不是观测时刻的地形特征，而是之前(或之后)较长时间间隔的地形数据，两者之间存在差异(比如，开采矿产或基础建设导致的局部地形变化，而通过已有地形图进行地形数据采集时这些变化又没有实时修正，局部地形变化导致的也就欠缺了)，甚至有时还相当大。由此产生的地形改正计算误差是一定存在的，这就导致实际计算的地形改正值与实际差异较大。再者，在进行地形改正值计算时，对于近区、中区、远Ⅰ区和远Ⅱ区，由于相应的范围大小不同，可是计算机的内存有限，计算程序的设置不能无限，即通过有限的存储空间，计算大范围、大数据量之地形改正值的工作量巨大，耗费时间也会很长，导致工作周期拉大，同样是参与具体工作的工作者不愿看到的。

第二，鉴于上述因素的存在，导致地形改正不完善，这也是大家在实际工作中所遇到的。从图4和图5看，未考虑地形影响的“简布格”和“自空”回归剩余异常的相关关系图5d较好，相关系数v>0.9995，说明两者是“同高”或者“同低”，且回归剩余异常的量值也是相同的。那么，再看“自空”和“布格”以及“简布格”和“布格”之回归剩余异常则呈现局部的“弱”相关和“负”(反)相关，由于相互之间仅考虑了地形影响，则极大可能是地形改正值(量)在作怪。

因此，在进行重力测量成果分析时，可以直接用“布格”进行数据分析，同时也要结合“简布格”和“自空”异常进行对比分析，加深各种数据之间的相互联系，提高重力测量成果资料的服务水平。

3.3 关于重力起算点问题

图6(a、d、g和b、e、h用文献中的公式计算)和图7(a、d、g和b、e、h用文献中的公式计算)分别为同一个测区两个不同起算点、同一(不同适用期)规范中相应计算公式计算所得“简布格”、“自空”和“布格”异常，再按照本文提出的方法进行回归分析的对比图。

a、b—“简布格”回归剩余异常；c—(a)和(b)相关系数; d、e—“自空”回归剩余异常；f—(d)和(e)相关系数；g、h—“布格”回归剩余异常；i—(g)和(h)相关系数

a、b—“简布格”回归剩余异常；c—(a)和(b)相关系数；d、e—“自空”回归剩余异常；f—(d)和(e)相关系数；g、h—“布格”回归剩余异常；i—(g)和(h)相关系数

从对比图看，对通过不同重力起算点所得重力异常(“简布格”、“自空”和“布格”异常)，其回归分析结果的相关程度较为一致，且用不同适用期的规范给定计算公式的计算结果进行回归分析后，其结果的相似程度亦较高。究其原因可能有如下两点：

首先，局部异常也就是浅部场源引起的异常，识别和提取方法也主要是突出此类异常，不论几种不同适用期的“规范”给定的计算公式的参数状态如何变化，在区域场之上叠加的局部场，归咎到底也就是叠加的变化，而叠加的变化也就是高程(起算点高程和测点高程)和高程差(测点高程与起算点高程的差值)的变化，通过异常值与高程(或高程差)进行回归分析，也就是提取出与高程变化量有关的场值而已。

其次，重力测量的理论基础即是场源和场源与待测点的距离的关系，地球是一个大场源，也就是重力测量工作的大背景场，那么，地球表面的高低不平，即表示观测点与场源中心的距离不一，其代表的即是与场源距离有关的背景场，且该背景场就是所有测点的“共有”(高低不平表示共有程度不同)，消除这个“共有”，即得到观测面以下局部场源的场值，也就是局部异常。

由此得出，在进行地面重力测量工作时，在资料整理过程中只要是能够反映出观测面位置附近的场源在重力测量成果中的变化量，不论运用哪一种计算异常的公式，运用回归分析提取出的回归剩余异常是没有变化的。

3.4 与传统消除区域场的方法比较

传统意义上的消除区域场的方法是以窗口(方域、圆域、环带等)滑动平均计算剩余异常的基础上得到的，窗口大小的选择具有人为性，且窗口的大小导致所消除的区域场是变化的。窗口选择愈大，所得剩余异常就愈接近于布格重力异常，而窗口选择愈小，不仅剩余异常的局部跳跃明显，区域场的跳跃也更明显。本文提到的消除区域场的方法，用研究区内的全部数据进行分析研究，其结果只有一种，不存在人为因素的影响。

另外，异常与高程之间的线性回归分析，实际并非只消除了异常与高程之间的线性关系，只是更加突出了观测场(异常)的剩余异常(局部高点更明显)，而通过数据采集所获得观测场，布格改正(高度改正和中间层改正)起主导作用的是高程的一次项(即线性项)，实测布格重力异常包含观测面的不平整(高程变化)影响因素，消除这个因素的影响结果更能突现出局部异常。

对于比较平坦的研究区，高程变化较小，由于观测场是变化的，不可因高程变化小而不做改正。再说高程变化虽然不大，但相对于经过布格改正所得到的布格重力异常仍是区域场，则消除区域场仍然是研究工作顺利进行的必要环节。

观测场是观测数据经过各项改正所得到的实测场，这里的各项改正在“五统一”的基础上进行的，其中布格改正与高程有关，而高程是变化的，但是这种变化引起的异常并非虚假异常，这一点毋庸置疑。