关于HPM课堂教学评价的案例分析

汪晓勤

(华东师范大学教师教育学院 200062)

1 引 言

近年来，随着数学史与数学教育(HPM)专业学习共同体的不断扩大和HPM教学案例的不断增加，数学史的多元教育价值以及HPM教学理念受到越来越多一线教师的关注.HPM课例开发遵循“选题与准备—研讨与设计—实施与评价—整理与写作”的流程，其中课例的评价采用了四维度评价框架[1][2]，这四个维度分别是“史料的适切性”、“方法的多元性”、“融入的自然性”和“价值的深刻性”.其中，“史料的适切性”是指教学中所使用的历史素材是否满足科学性、可学性、有效性、人文性和趣味性，“方法的多元性”是指是否采用附加式、复制式、顺应式和重构式来运用数学史；“融入的自然性”是指数学史的运用是否实现了逻辑序、历史序和心理序的有机统一；“价值的深刻性”是指课堂上数学史是否有助于构建知识之谐、彰显方法之美、营造探究之乐、实现能力之助、展示文化之魅和德育之效.上述框架完全是“自下而上”得出的，还缺乏扎实的理论基础，且与数学教育领域已有的课堂评价方式之间缺乏密切的联系，因而还有很大的完善空间.

美国学者熊菲尔德(A. Schoenfeld)和他的研究团队提出“为强有力的理解而教”(Teaching for Robust Understanding，简称TRU)的课堂评价框架，该框架包含数学内容、认知需求、学习机会、学生表现和评价运用五个维度[3][4][5].本文融合原有的四维度评价框架和TRU评价框架，建立更为合理的HPM教学评价框架，并将其应用于HPM课例——“三角形的中位线”，以期为未来的HPM课例研究提供指导.

2 从TRU框架到HPM教学评价框架

表1给出了熊菲尔德用和他的团队建立的TRU课堂教学评价表[3][4][5].其中，“内容呈现”对应于“教什么”，“认知需求”、“学习机会”和“评价运用”对应于“怎么教”，“学生表现”对应于“怎么学”.整个框架具有鲜明的“以学生为中心”的特点.

表1 “为强有力的理解而教”的课堂评价框架

为了将TRU框架用于HPM课例的评价，需要将数学内容替换为与数学史相关的教学内容.与“数学内容的准确、连贯与合理性程度”相对应的，就是“数学史料的准确、连贯和合理性程度”，即四维度评价框架中的“史料的适切性”；教师如何利用数学史料设计和组织课堂活动为学生理解和掌握数学概念提供支持，与四维度框架中“方式的多元性”和“融入的自然性”相对应.

四维度框架并没有专门关注“学习机会”，而“方式的多元性”只是与“评价运用”部分相关；从学生表现可以看到数学史在课堂上实际体现的价值，因而“价值的深刻性”与“学生表现”之间则是“应然”和“实然”的关系.根据TRU评价框架，我们建立HPM课例评价的新框架，见表2.

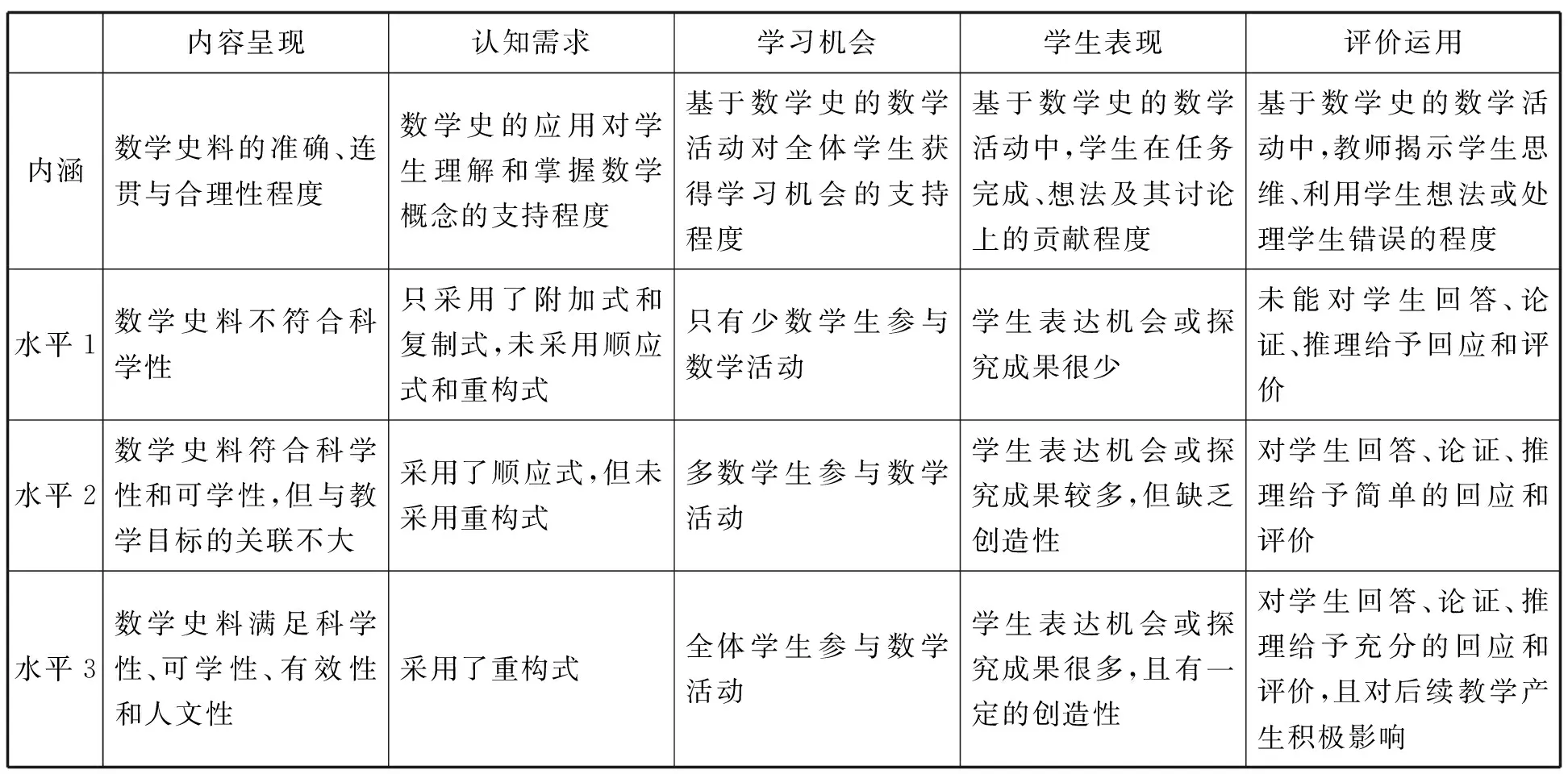
表2 HPM课堂教学评价新框架

3 案例分析

我们以 “三角形中位线”一课为例，来说明HPM课例评价框架的应用.

3.1 内容呈现

我们从科学性、可学性、有效性和人文性四个子维度来看本节课所用的数学史料.

其一，本节课所涉及的数学史料有数学问题(三角形面积问题)、数学定理(三角形中位线定理的历史、瓦里尼翁与中点四边形)和数学方法(出入相补法、面积法).数学问题出自《九章算术》方田章；数学定理的历史根据古巴比伦、古希腊、中国古代、17-18世纪欧洲的数学文献、早期美英几何教科书中的有关内容整理、归纳而成；数学方法中，出入相补法出自刘徽《九章算术》方田章“圭田术”注(图1)，面积法出自欧几里得《几何原本》

图1 《九章算术》书影(影印四库全书版)

卷六命题2(图2)；中点四边形定理出自18世纪法国数学家瓦里尼翁(P. Varigonon, 1654-1722)的《数学基础》(1734，图3).因此，本节课涉及的数学史料都具备科学性.

图2 《几何原本》书影(希思注释版)

图3 瓦里尼翁《数学基础》以及书中的插图

其二，由于三角形面积公式是学生十分熟悉的内容，尽管教师呈现了《九章算术》原文，但经过解释，学生在理解上毫无困难；历史上数学家所给出的各种方法都是通过学生自主探究再现于课堂的，而非教师的灌输；三角形中位线定理的历史通过HPM微视频呈现，为学生所喜闻乐见，其中所介绍的定理证明方法，与学生所采用的方法相对应；瓦里尼翁四边形则是三角形中位线定理的直接应用.可见，本节课所涉及的数学史料符合学生的认知基础，具备可学性.

其三，教师采用《九章算术》中的三角形面积问题三角形面积公式，对应于“经历三角形中位线概念的形成过程”这一教学目标，并为“经历三角形中位线定理的探索过程”这一教学目标埋下伏笔；刘徽的出入相补法和欧几里得的面积法，对应于“经历三角形中位线定理的探索过程”、“培养学生的逻辑推理素养”以及“理解从特殊到一般和转化的数学思想”的目标；瓦里尼翁中点四边形对应于“应用三角形中位线定理解决问题”的目标；中位线定理的历史发展概貌，则对应于“感受数学文化的多元性、体会数学背后所蕴含的理性精神”的目标.因此，本节课所运用的数学史料完全服务于教学目标，具备有效性.

其四，本节课所涉及的历史素材，都与数学家相对应，凸显三角形中位线定理发展过程中数学家的作用，并揭示定理所蕴含的理性精神，具备一定的人文性.倘若教师在教学中进一步引发学生思考“为什么不同时空的数学家会不断地去探究新方法”这一问题，对于人物的生平事迹也有涉及，则数学史料的人文性将得到加强.

总的说来，本节课在“内容呈现”维度上，基本达到了水平3.

3.2 认知需求

在数学史素材的运用方式上，本节课主要采用重构式来促进学生对概念、定理的理解与运用，并在重构的过程中，兼用了附加式、复制式和顺应式.

该找一个什么借口和她搭讪呢？说没有位子直接坐到她的对面吗？可是位子明明很富余呀。跟她打听点什么事情吗？可是能打听什么呢？跟她借点什么小东西吗？都什么年代了，哪有随便跟陌生人借东西的？再说了，男人能借的除了打火机还能是什么？在中国跟一个女子借打火机又算什么？咖啡厅不是不可以抽烟的吗？哎呀！

从历史上看，几何概念往往经历从“无意识几何”到“实验几何”、再到“演绎几何”的过程.古巴比伦泥版书记录了许多三角形土地分割问题，人们在分割土地的实践中，已经不自觉地应用了三角形中位线，但并未正式提出过“三角形中位线”的概念和性质，故属于“无意识几何”阶段.

虽然在古巴比伦泥版书和欧几里得《几何原本》之间相关史料是缺失的，但正如三角形内角和定理源于现实生活中的铺地砖(图4)一样，三角形中位线定理也可能有同样的起源.如图5所示，将四个同样的三角形拼成一个三角形，易于从中发现三角形中位线与底边之间的大小关系.显然，这样的发现过程属于“实验几何”阶段.中国古代数学家刘徽在推导三角形面积公式时也应用了中位线，但他所实施的“以盈补虚”操作，就三角形中位线定理而言，亦属于“实验几何”阶段.

图4 六个同样的三角形拼成一个六边形

图5 四个同样的三角形拼成一个三角形

欧几里得在《几何原本》卷六中严格证明了命题2：“将三角形两腰分割成成比例的线段，则分点连线段平行于三角形的底边.”[4]显然，三角形中位线定理是该定理的特殊情形，欧几里得的面积证明同样适用，这标志着中位线定理进入“演绎几何”阶段.

本节课对三角形中位线定理的历史发展过程进行了重构，如图6所示.教学中，这个重构的过程是通过“三角形面积的推导”“中位线定理的证明”和“中点四边形面积的探究”三个探究活动来实现的.

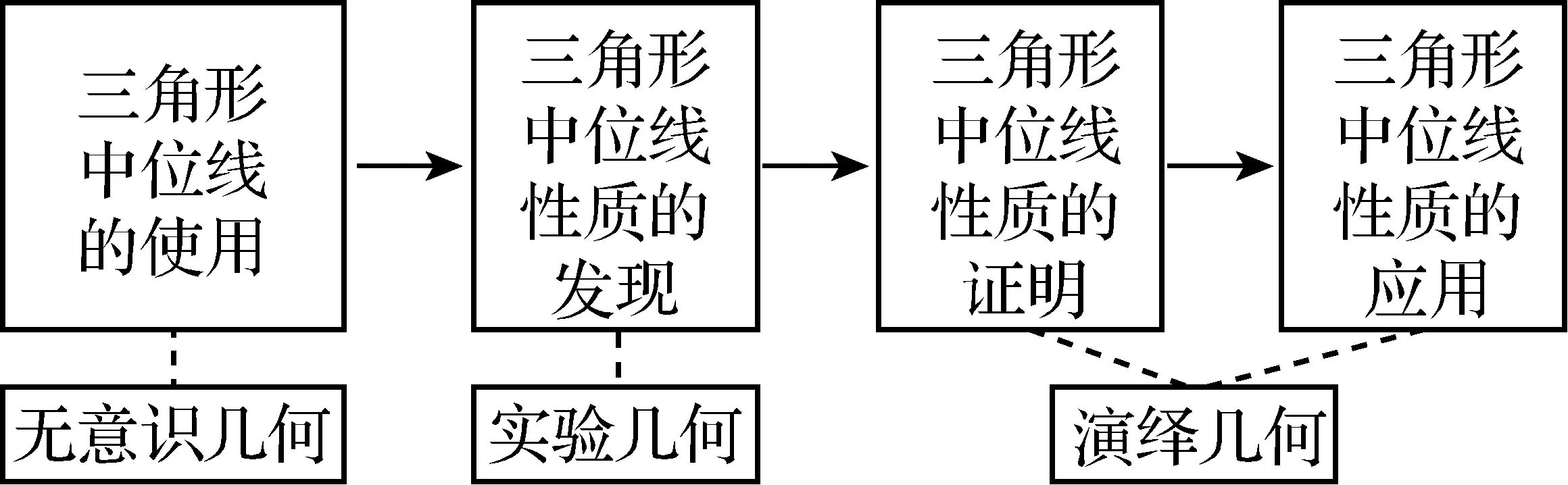
图6 三角形中位线定理产生与发展过程的重构

在第一个探究活动中，教师采用了《九章算术》中的原始问题，属于复制式，证明“圭田术”的问题，属于顺应式，对于学生推导三角形面积公式所采用的方法，教师通过“古今联系”的策略加以评价，属于顺应式.在第二个探究活动中，对于学生证明中位线定理的不同方法，教师也采用了“古今联系”的策略加以评价，故属于顺应式.在第三个探究活动中，教师根据瓦里尼翁中点四边形，提出新的面积问题，属于顺应式.HPM微视频的运用则属于附加式.

要满足学生的认知需求，教师需要为学生提供足够的思维空间，即充分“留白”.本节课中，教师通过数学史的四种运用方式，为学生留出“发现之白”、“论证之白”和“方法之白”，有效地促进了学生的学习.

总的说来，本节课在“认知需求”维度上达到了水平3.

3.3 学习机会

一枝独秀不是春，百花齐放春满园.将数学史融入数学教学，不是让少数学生受益，而是为全体学生创造学习机会.本节课中，探究活动分组开展，组内研讨、全班交流、个体展示、生生交流，绝大多数学生都有机会表达自己的想法，所有的学生都积极参与到活动之中.通过在线研讨、课堂观察以及课后与执教者的交流发现，有四个因素导致本节课在“学习机会”维度上取得成功.

一是教师的HPM教学理念.比利时-美国著名科学史家萨顿(G. Sarton, 1884-1956)曾经指出，数学史研究的主要目的是揭示数学的人性(humanity).数学史告诉我们，数学研究乃是人类的一种文化活动，是人在做数学，是人在创造历史.HPM以沟通历史与现实、融合数学与人文、创建人性化课堂为目标，其基本教学理念是教学的实施即文化活动的实施，以学生为中心，给予他们探究机会，让他们经历新知的发生和发展过程，从而将历史再现于课堂.本节课充分体现了这一理念.

二是基于数学史的探究任务的设计.本节课采用“温故知新”策略来设计探究任务：三角形面积公式的推导为“温故”，推导过程中使用了中位线并导致中位线性质的发现，为“知新”(图7).“温故”需要关注学生的认知基础，“知新”需要激发学生的学习动机，“温故知新”为全体学生的参与提供了保障.

图7 温故知新

三是 “同侪学习”的组织形式.本节课上，探究活动是按照小组合作(四人一组)的形式开展的，每一小组都需要汇报本组的探究成果，每一小组都需要倾听其他小组的汇报，当一个小组在某个地方被“卡住”时，别的小组需要予以解决.例如，当一个小组展示面积证法(下一节方法6)时，只证明了中位线与底边的位置关系而未能解决大小关系，另一小组给予了补充，从而完善了证明.为了小组的荣誉，每一位学生都需要贡献自己的智慧.四是学生本身的知识基础.同样一份HPM视角下的教学设计，在不同层次的学校实施的效果互不相同，很多时候，当学生的基础较弱或数学情感比较消极时，学生参与度会较低，这种情况下，为了增加全体学生的学习机会，教师需要对教学设计加以改进.本节课的成功，部分得益于学生良好的基础.

总的说来，本节课在“学习机会”维度上达到了水平3.

3.4 学生表现

本节课中，学生的表现主要体现在探究过程和结果上.探究活动1中，学生通过拼图得到三角形面积公式的两种推导方法：一是将三角形转化为平行四边形，二是将三角形转化为矩形(图8)，无意中都为三角形中位线性质的发现和证明埋下了伏笔.基于探究活动1中的方案，学生很快猜想出中位线的性质.在探究活动2中，学生相继给出六种方法证明中位线性质(图9)：方法1是课本上呈现的方法，是人们最常见的方法；方法2和3分别通过作中位线上的高线和中线，将以中位线为底边的小三角形进行分割，从而将原图形转化为矩形和平行四边形；方法4则是通过中位线上的任意一点与顶点的连线对小三角形进行分割，是对方法1-3的一般化、动态化.对于各种方法，学生都能够完整地表达证明的过程(图10)，气氛活跃，精彩纷呈.

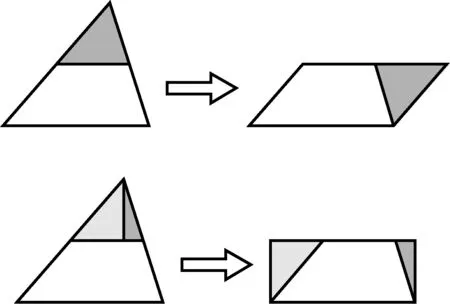
图8 三角形面积公式的推导方案

图9 学生关于三角形中位线定理的不同证明

图10 学生展示三角形中位线定理的不同证明

方法5分别过两腰中点作底边的垂线，从而将原三角形转化为矩形，但学生未能像方法4那样将该方法进行一般化、动态化.事实上，如图11所示，过两腰中点任作两条平行线，都可以证明中位线定理.

在探究活动3中，学生证明了中点四边形的形状，但由于没有足够的时间，他们未能用等积变形得出中点四边形的面积.

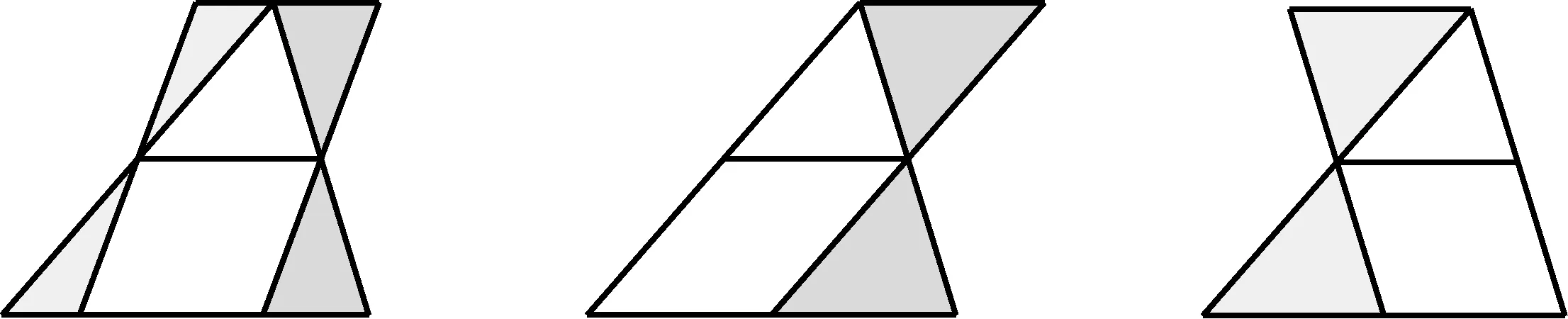
图11 方法5 的一般化(课堂上没有出现)

总的说来，本节课在“学生表现”维度上达到了水平3.

3.5 评价运用

本节课中，教师采用“古今联系”的策略来评价学生的探究成果.学生的方法2和方法5与刘徽的两种出入相补法完全一致(图12)，方法6的第一部分再现了欧几里得的方法.方法4 将方法1-3囊括其中，是对历史的完美超越.方法6的第二部分解决了《几何原本》未涉及的中位线与底边的大小关系，是对欧几里得方法的精彩补充.“古今联系”策略让学生仿佛穿越时空与数学家对话，既再现历史，又超越古人，有效地激发了学生的兴趣，增强了学生的自信心.此外，本节课中，“同侪互评”往往代替教师的评价，成了本节课的亮点之一.

图12 古今联系

但本节课中，尽管“古今联系”和“同侪评价”对学生产生了积极的影响，但对于后续教学，特别是中点四边形的探究，并未产生显著的影响.因此，本节课在“评价运用”上与水平3尚有一定的差距.

4 结语

综上我们看到，融合TRU框架和HPM四维度评价框架后所形成的新框架，涉及“教师教什么”、“教师怎么教”以及“学生如何学”，可用于HPM课例的评价；与旧的四维度评价框架相比，新框架更加关注学生的学习过程，并且避免了旧框架中“融入的自然性”和“价值的深刻性”两个维度的主观性，可操作性更强，因而更适用于教研活动.当然，该框架还需在未来的HPM教研实践中进一步加以完善.

对HPM课例的评价，主要关注与数学史相关的教学内容、教学方式、学习过程与教学成效.但从HPM视角设计和实施的一节课毕竟是数学课，而不是数学史课，不可能从头到尾都与数学史相关.因此，评价过程中需要注意与数学史相关的教学内容和无关数学史的教学内容的区别，客观地呈现数学史在教学中所扮演的角色.