高中基本不等式研究的回顾与展望①——基于中国知网中文核心期刊②文献的统计分析

于晓宇 李春兰

(内蒙古师范大学数学科学学院 010022)

1 前言

基本不等式联系着代数和几何中的两个基本量——算术中项、几何中项，涉及数学的基本运算(加法、乘法、除法、开方)，还具有以下特点.首先，基本不等式的证明方法层出不穷.“AG不等式(1)算术-几何平均值不等式，又名AG不等式.各种不同的证法一直是人们研究的一个热点……事实上至今已有上百种不同的证明方法.”[3]其次，基本不等式的应用十分广泛，尤其在求最值的问题中，且在其他很多学科中都有不可或缺的作用.1986年的《全日制中学数学教学大纲》首次要求学生掌握二元和三元的算术-几何平均值不等式，《普通高中课程标准实验教科书·数学》(2004年版)必修教科书只要求学生掌握二元形式，即基本不等式，将三元和多元的算术-几何平均值不等式编排在了选修中.虽然基本不等式出现在教学大纲中的时间偏晚，但其涵义——“和定积最大”，却早在1952年就已经出现在我国的教科书中了.

综上，基本不等式的重要性可见一斑.因此很有必要对以往高中基本不等式的研究文献进行系统的统计梳理与研究，总结研究取得的成果，展望可能的研究方向，为高中基本不等式的教学与研究提供借鉴与思考.

2 研究设计

2.1 数据采集

要回顾高中基本不等式研究的发展历程并展望其发展，以核心期刊中有关高中基本不等式的研究文献作为研究对象，应是可靠的数据来源.正如叶继元所言：“核心期刊是本学科中刊载专业论文量大，引用率高，代表该学科领域发展水平的少数期刊.”[4]考虑到核心期刊会不断更新，为了保证研究的可靠性，主要采取人工筛选的方式进行文献检索.

研究过程中使用中国知网进行文献检索，在高级检索条件下，篇名或关键词分别选择“基本不等式”“均值不等式”“均值定理”“平均值不等式”，期刊范围选择“核心期刊”；普通检索条件下，篇名分别设置为上述4类，将得到的文献进行人工筛选.截止到2020年12月22日，两种检索方式共筛选出115篇发表在核心期刊上的基本不等式研究文献.然后泛读所有搜集到的文献，剔除高等数学范围内，以及非高中阶段要求掌握的基本不等式(算术-几何平均值不等式)的研究文献，得到61篇高中基本不等式研究论文.

2.2 研究方法

借鉴牛伟强[5](2017)和陆珺[6](2019)等人文献分析的维度、参考朱立明[7]文献述评的特点，并结合本研究具体情况，将分析维度划分为年代分布、期刊分布、作者情况、研究类型和研究内容五个方面.将61篇文献编码便于统计和查找，再次泛读文献，按照分析维度记录相关内容.两轮泛读之后，有34篇精读文献被纳入文献研究范畴.

首先，使用内容分析法对61篇文献的内容进行客观、系统和量化的描述，用直观的图表展现高中基本不等式研究相关维度的变化历程.其次，使用文献研究法，对两轮泛读后确定的34篇精读文献进行分析和整理，进一步掌握前人已取得的研究成果以及现行的研究状况等.最后，分析和展望高中基本不等式研究的发展方向.

3 结果与发现

3.1 年代分布

分析文献的年代分布不仅能从宏观上回顾某一研究的文献分布情况，还能从图表中了解其动态的变化趋势.对搜集到的61篇文献进行年份统计(如图1).

图1 发文篇数年代分布

由图1发现高中基本不等式研究文献发表的时间范围为1992—2020年，时间跨度达30年，不少年份发文数量为0篇，年均发文量只有2篇，可见高中基本不等式研究年均发文量很低.根据图1，1992—2020年间发文量明显的增长发力点位于1993年，这应该与1993年的高考数学试卷中编排了一道利用基本不等式求函数最值的题目不无关系，在1995年达到峰值，但峰值也只有9篇，之后骤降，只有2000年发文数量超过5篇，2010—2014年连续5年的发文总量只有2篇，可谓是高中基本不等式研究的冰冻期.

3.2 期刊分布

统计发现61篇高中基本不等式研究文献分布在9种核心期刊(见表1)，其中仅2篇来自CSSCI来源期刊(含拓展版)(2)《数学教育学报》在2014年成为CSSCI扩展版来源.因此2009年发表在《数学教育学报》的1篇文章并不是来自CSSCI来源期刊(含拓展版)..发文量最多的是《数学通报》，其次是《数学通讯》和《中学数学》.表1中前3种期刊共发文51篇(83.61%)，可见这3种期刊是高中基本不等式研究的主要发文核心刊物.

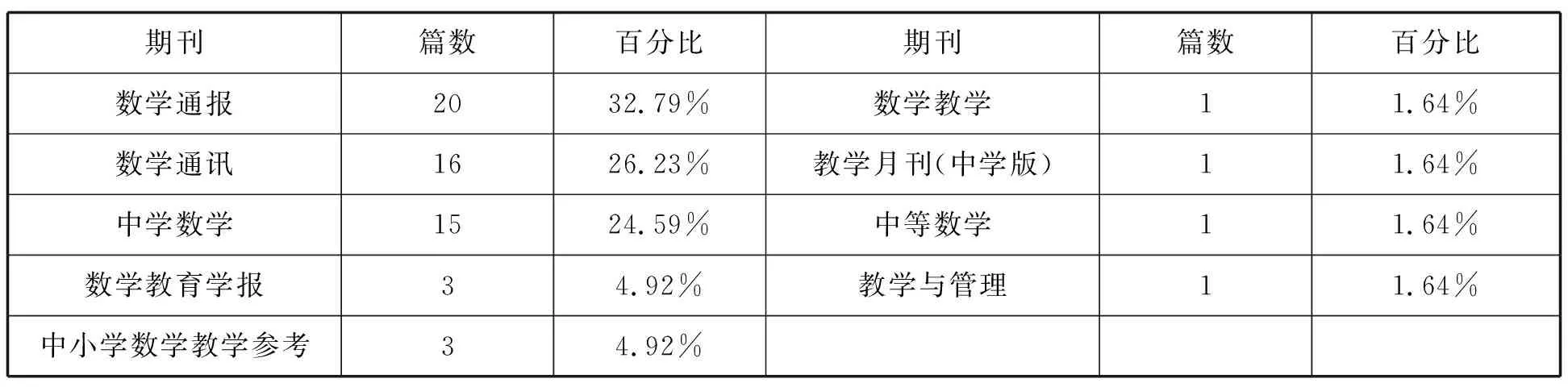
表1 高中基本不等式研究期刊分布

3.3 作者情况

作者的学术水平是文献研究水平的主要决定因素之一.从第一作者的机构、地区和合作情况三个角度分别对高中基本不等式研究的61篇文献进行统计.

3.3.1 作者机构分布

按第一作者单位对研究文献进行统计(见表2). 由表2可知，高中基本不等式研究文献的主要发文机构为中学校，发文量达47篇(77.05%).相比之下，高等院校发文较为零散，其中只有2所“211”“985”高校，各发文1篇.可见，中学教师是研究的主要力量，而高校教师却较少参与到基本不等式的研究中.

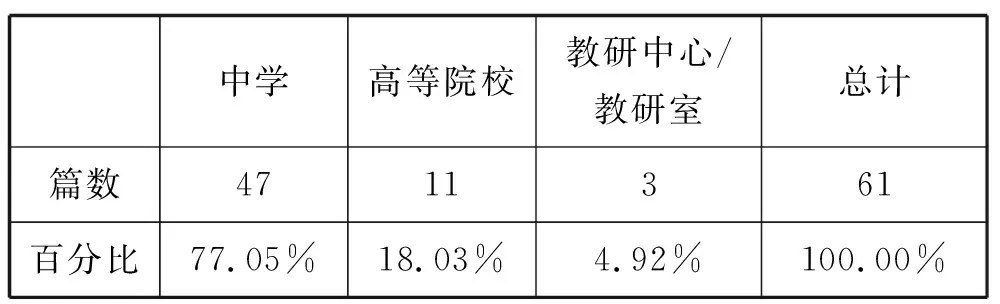
表2 高中基本不等式研究机构分布

3.3.2 作者地区分布

按第一作者所在行政区对研究文献进行统计(见表3).共涉及21个省、直辖市，文献产量从9篇到1篇不等，我国5个少数民族自治区中只有广西壮族自治区包含1篇文章.将表3的结果按东、中、西部的三大地理区域进行划分(见表4)，发现来自东部发达地区的文献共有37篇(60.66%)，而来自西部经济欠发达地区的文献数量最少，只有8篇(13.11%).可见教育研究人员的科研成果和方向在一定程度上受该地区的经济发展水平影响.

表3 第一作者行政区分布

表4 第一作者地理区域分布

3.3.3 作者合作情况

高中基本不等式研究以个人独立研究为主，合作研究较少(见表5).有49篇文献为作者独作(80.33%)，合作的文献只有12篇(19.67%). 在合作研究的12篇文献中，从作者身份来看，中学教师合作的有8篇(66.67%)，高校教师合作的有4篇(33.33%)，并未发现有高校教师与中学教师合作的文献.从作者工作单位来看，校内合作、跨校合作分别有6篇，在跨校合作中，有3篇是跨省合作，既包括中学教师的跨省合作，也包括高校教师的跨省合作.

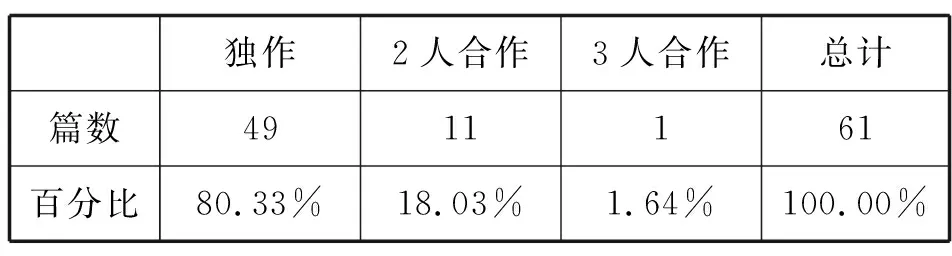
表5 高中基本不等式作者合作情况

3.4 研究类型

将61篇文献中涉及到的研究类型分为思辨研究、实证研究、历史研究和案例研究，并进行整理和统计(见表6).

由表6可知，高中基本不等式研究文献的研究类型主要以思辨研究为主，共有51篇文献(83.61%)，而实证研究、历史研究和案例研究的占比较小，说明有关高中基本不等式的研究类型较为单一，使用实证研究、历史研究和案例研究等类型的文献也很匮乏.

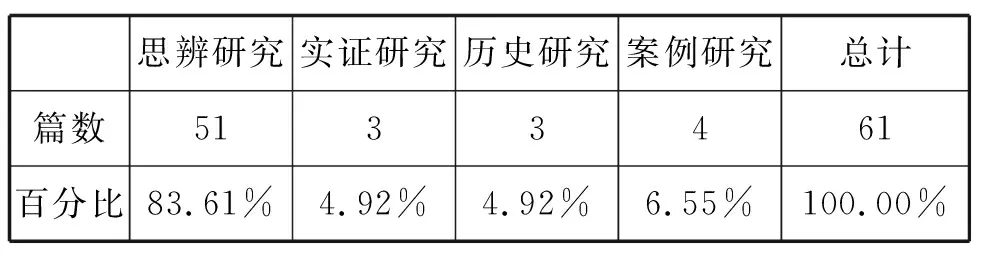
表6 高中基本不等式研究类型

对涉及到的研究类型按年代再进行整理(如图2)，在2008年以前，有关高中基本不等式研究文献的类型以思辨研究为主，1992—2008年间发表在核心期刊上的高中基本不等式研究文献共48篇，其中2篇分别是历史研究和案例研究，其余均为思辨研究.2009—2020年间共发表13篇文献，其中8篇文献采用了思辨研究之外的研究类型，并且在这期间还新增了实证研究的类型.从2009年开始，研究类型逐渐多样化，可见，学者们越发地关注到了基本不等式的价值所在.

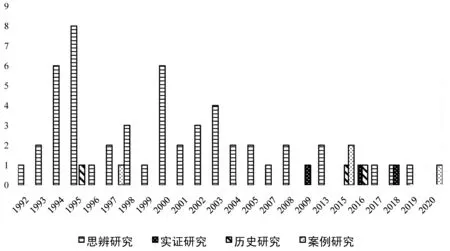
图2 研究类型年代分布

3.5 研究内容

3.5.1 内容分析结果统计

对搜集到的61篇文献进行系统的梳理和分析，发现关于高中基本不等式的研究主要集中在四个方面，按年份将研究内容整理(见表7).基本不等式的应用研究可谓是最“热”的研究话题，数量占到总文献的60.66%；其次是基本不等式的教学(19.67%)、证明(13.12%)及认识角度(6.55%)的研究.

表7 研究内容分布

高中基本不等式的应用又可以细分为5类，其中文献数量最多的3类是用基本不等式求最值(19.67%)、解决多种问题(14.75%)和证明不等式(14.75%)，总和已经接近文献总数的一半.最后按统计结果可以笼统地将9类研究内容分为3个数量层级.第1层级是10篇及以上，包括用基本不等式求最值和教学研究；第2层级是6-9篇，包含用基本不等式证明不等式、解决多种问题和非历史角度证明研究；第3层级是1-5篇，包括用基本不等式解决实际问题和错解研究、基本不等式的认识角度研究和历史角度证明研究.因此，研究人员更加关注的是利用基本不等式求最值和基本不等式的教学，而根据研究内容的年代分布图(如图3)可以看出，基本不等式的教学研究在最近几年引发了一波热度，从2015年开始，几乎每年都有学者从教学角度研究基本不等式.而应用研究似乎已经达到饱和，从2009年开始便一直处于低潮期.基本不等式的证明方法虽然多种多样，但是一直并未引起足够的关注.

图3 研究内容的年代分布

3.5.2 文献研究述评

(1)基本不等式的应用研究

基本不等式的应用是学者们偏爱的研究主题，相关研究文献数量有37篇(60.66%)，达到文献总数的一半以上.一方面，学者们利用基本不等式证明其他不等式，其中包括著名不等式——贝努利不等式(谭登林，1993)和数学竞赛中的不等式证明(刘祖希，2003等)等经典题目.

另一方面，基本不等式还是解决最值问题的有力工具.关于求函数最值，多数学者都是将所求最值函数进行一定的变形(毕明黎，1996等)，再巧妙运用基本不等式求得最值.还有学者从基本不等式本身出发，如巧妙设置带参数的基本不等式(邓光发，1998)等方法来求得函数最值.除了求函数最值，基本不等式也能求圆锥体积的最大值(杨志明，2003)、解决许多实际应用问题(赵存善，2003等).

上述证明和求解等问题都是学者们单独在某篇文章中进行讨论的，也有很多学者在一篇文章中同时讨论几类基本不等式的应用问题(明知白，1995等).这些问题多数来自教科书中题目改编、高考题、数学竞赛问题和实际问题等，题目类型也十分多样.除此之外，部分学者(陈东升，2008等)则是讨论了基本不等式的错解，以指出错因并改正.

从这些文献中可以发现，基本不等式的应用的确十分广泛，并不局限于证明不等式和求最值的问题中，学者们用开阔的思维，为我们展现出了一个华丽的基本不等式应用的舞台，让基本不等式自由地徜徉于数学的海洋中.

(2)基本不等式的证明研究

基本不等式的证明一直是数学家们感兴趣的研究内容之一，几何证明方法也渗透着数形结合的思想.整理发现有关基本不等式证明的文献有8篇(13.12%).贺贤孝(1995)和沈金兴(2016)都站在历史的角度论述了基本不等式的证明方法，但二者论述角度略有不同.贺贤孝只是总结了数学家曾证明基本不等式的方法，沈金兴却站在巨人的肩膀上，修改或借鉴前人的证明方法，目的是为了使其更适合课堂教学.不得不说，证明方法“花样百出”是基本不等式的一大亮点.除了借鉴前人的证明方法，很多学者也通过自己的思考探索出了多种基本不等式的证明方法，例如，刘会丰(2008)以“构造法”为线索，探索出了如构造二次方程、构造函数、构造图形等证明基本不等式的方法.

(3)基本不等式的教学研究

有关基本不等式教学研究的文献有12篇(19.67%)，都是以基本不等式为例来探讨教学中的其他问题.这部分文献的研究类型相比于前两类研究较为多样，包含了思辨研究、案例研究和实证研究三种.

采用实证研究类型的文献有3篇，张伟平(2009)从基本不等式中的“等号”出发，以大一新生为实证研究对象，调查了学生对等价思想的认识；黄娅(2016)从教师知识掌握的角度出发，针对“基本不等式”内容，对教师的“面向教学的数学知识(MKT)”进行了问卷调查和访谈；张令伟(2018)等将高三学生作为被试对象，探讨了基本不等式问题特征的不同相似关系对解题迁移的影响.

采用案例研究类型的文献有4篇，李正池(1997)和蔡欣(2015)记录了自己讲授 “基本不等式”的一节课.张蜀青(2015)则是记录了三节分别由两名中学教师和一名大学教师讲授的基本不等式公开课，通过“同课异构”，分析了中学教师与大学教师不同的讲授方法和其中暗含的教育理念.吴佐慧(2020)从HPM的新颖视角出发，通过数学史微视频以及探究活动等对基本不等式的教学进行了一次尝试.

其余文献均为思辨研究，以基本不等式教学为例探讨了教学中例如怎样培养灵感(李德钦，2001)、如何在教学中践行“三个理解”(陈义明，2017)、如何进行变式教学(钟志华，2019)等问题.其中余小芬(2018)以基本不等式一节为例，给出了创造性使用教科书的几种思路，并倡导读者大胆地对教科书进行二次开发.

从以上文献可以看出，有关基本不等式的教学研究，不论是从研究内容还是研究类型来看，都展现出了更加千姿百态的形式.

(4)基本不等式认识角度的研究

基本不等式结合了数学中的两个基本量——算术平均值和几何平均值，虽然看似结构简单，但却蕴含着十分丰富的内容.这类文献共有4篇(6.55%)，学者们虽然并未对基本不等式进行严格证明，却用别具一格的视角，带领读者重新认识基本不等式.其中几何视角占领更广阔的位置.例如，徐章韬(2004)和汪晓勤(2015)都是从几何方法入手，而汪晓勤则是从勾股容方图出发，得到了探究基本不等式的几何方法，同时启示读者：带着HPM的眼光去阅读数学历史文献能够为教学甚至我们的思想带来鲜活的养料.方亚斌(2013)从代数、方程、统计、向量等9个视角来认识基本不等式，视角更加多元和丰富.

4 反思与展望

纵观1992—2020年高中基本不等式研究，以时间为线索，研究内容和研究类型逐渐多元化.一方面，2008年以前的研究大多集中于基本不等式的应用，研究类型主要以思辨研究为主，从2009年开始，有关基本不等式的教学研究增多，研究类型更加多样.另一方面，早期的研究作者以中学教师为主，但近年来高校研究者也陆续参与到基本不等式的研究中.总之，有关高中基本不等式的研究持续时间久，研究内容、研究类型和合作情况等都表现出向好的态势，取得了一定的研究成果，但年均发文量却非常低，仍有很多问题值得关注.

4.1 现有研究的不足

首先，高中基本不等式研究论文的数量有待提升，研究类型有待丰富.统计发现高中基本不等式的年均发文量只有2篇，发表在CSSCI来源(含扩展版)期刊上的文献更是屈指可数，可见高中基本不等式还应该受到学者的更多关注.另外，虽然近年来文献的研究类型趋于多样化，但现有的文献类型主要还是以思辨研究为主，占全部文献的83.61%，因此在研究类型的选择和应用上还有待丰富和加强.

其次，高中基本不等式研究人员地区、机构分布不均衡且缺乏合作.研究人员大多来自东部经济发达地区，而中西部地区的研究成果却严重偏低，且中学教师是高中基本不等式研究的主力军.高等院校研究人员学术水平更高，无论是研究能力还是在研究方法的运用上都要更加专业，而中学教师又是教学的第一实践者，针对教学实践最有发言权.但目前高校研究人员与中学教师的合作还是个缺口.

最后，高中基本不等式研究内容关注程度不平衡.在搜集到的61篇文献当中，有37篇关于基本不等式的应用研究，占全部文献的60.66%，且研究重复率较高，许多研究成果只是“换汤不换药”.基本不等式的证明方法涉及几何代数等多个方面，具有重要的研究价值，但基本不等式的证明、教学等其他研究内容受到的关注度却偏低.

4.2 未来研究的展望

第一，注重基本不等式教学的实证和案例研究.基本不等式结构简单，但证明方法多样，不仅在中学数学证明不等式和求最值问题上应用广泛，还在高等数学的求极限、证明积分不等式方面发挥着独特的作用.因此基本不等式具有十分重要的教学价值，那么如何教学才能让学生在后续学习中将基本不等式的内容做到融会贯通？甚至为将来选择理工科、学习高等数学的学生奠定基础？这些问题仍值得探讨.未来的研究应以此为着眼点，注重基本不等式的实证和案例研究，将基本不等式的教育价值最大程度地发挥出来.

第二，加强基本不等式的教科书研究.“教材的编写与研究是教材建设工作相互联系的两个方面，前者为后者提供素材并展现其成果和水平，后者则为前者提供科学基础昭示其改进方向.”[8]一直以来，国内各版本、国内外不同版本教科书内容的比较研究都十分盛行，但基本不等式相关内容的教科书研究还未全面展开.据一线教师反馈，虽然基本不等式在教科书中所占比例非常小，但却是高中数学学习不可替代的重要内容之一.针对教科书对基本不等式的编排设置，有的教师认为其必修和选修内容设置重复，有的虽认为教科书的设置较为合理，但建议教学要切忌照本宣科.同时，以人教A版高中数学教科书为例，历年各套教科书对基本不等式的设置编排也经历着一定的变化，其中缘由还应深入研究.因此基本不等式在教科书中的安排设置研究是很有必要的，不仅能够为教科书编写提供参考，还能为一线教学带来启示.

第三，重视基本不等式的HPM研究.基本不等式不仅是高中数学的重要内容之一，其多元形式——算术-几何平均值不等式更是高等数学中的一块奠基石，而有关基本不等式的HPM研究却寥寥无几，其中汪晓勤教授和其团队贡献了更多的力量.“数学的历史是一座宝藏，从中可以发掘出取之不尽、用之不竭的教学资源.”[9]从历史中可以获得基本不等式多样的证明方法，还能将其他数学历史资源与基本不等式相联系，就如人教A版高中数学教科书就将赵爽弦图与基本不等式相联系，可见依然还有丰富的有关基本不等式的HPM资源等待挖掘.HPM研究不仅能丰富课堂教学，还能使学生乐学、好学，让原本看上去冰冷的基本不等式发挥独特的教育价值，为素质教育和立德树人提供良好的实施契机.