基于混沌理论的岸桥铰点状态识别方法

陈晴岚，胡 雄，王 冰

（上海海事大学物流工程学院，上海201306）

岸边集装箱起重机（岸桥）通常采用俯仰式的前大梁结构形式，前后大梁之间采用铰点连接，大梁上的小车轨道在铰点处断开，并留出一定的间隙，以保证前大梁被拉起时活动不受限制［1-2］。岸桥小车经过此处间隙时，不可避免地产生振动，使铰点区域承受剧烈的冲击。在长期频繁的冲击下，铰点区域内的部件可能发生松动、变形甚至损坏，加剧噪声和冲击振动，影响岸桥的安全运行［3］。因此，关注铰点的状态十分必要。铰点处的振动信号具有强烈的非线性、非平稳性的特点，很难利用传统的线性方法和频域分析方法对其进行分析，部分研究者尝试运用时频分析方法［4-5］或从统计学的角度［6］对其进行分析，在特征提取和状态评价方面取得了一定的进展。

鉴于混沌理论在多个领域内分析非线性、非平稳信号的成功运用［7-12］，笔者尝试运用混沌理论的方法对铰点振动信号进行分析。首先识别铰点振动信号是否具有混沌特性，在此基础上，对比分析不同状态下铰点振动信号的最大Lyapunov指数和混沌吸引子结构特征，探究运用混沌理论对铰点工作状态进行识别的有效性。

1 相空间重构技术

相空间重构是研究混沌时间序列的基础。Packard 等［13］提出，选取适当的延时值可以由一维时间序列重构相空间，用以从时间序列中提取更多有用的信息。Takens 定理表明：只要找到一个合适的嵌入维m≥2d+1（d为动力系统维数），便可在这个嵌入空间中把原系统的吸引子恢复出来，即在重构相空间中的轨线与原动力系统保持微分同胚［14］。相空间重构的具体原理如下：

设一维时间序列为{xi|i=1，2，…，N}，其中，N为时间序列的长度。选择合适的延迟时间τ和嵌入维数m，可将该一维时间序列重构为

式中：n=N-(m-1)τ为重构相空间中相点的个数；X中的每一行构成m维相空间中的一个相点。

对于无限长且无噪声的时间序列，嵌入维数m和延迟时间τ可以取任意值，但是实测的铰点振动信号的长度都是有限的，且存在大量噪声。因此，必须通过特定的方法计算合适的嵌入维数m和延迟时间τ。

1.1 延迟时间的计算

在相空间重构的过程中，若τ过小，重构相空间中相轨道间的相关性太强，相轨道被压缩，无法展示系统的动力特性；若τ过大，重构相空间中相轨道将变得毫不相关，相邻相轨道分叉，导致系统状态信息丢失。本文选择互信息法［15］计算延迟时间τ，该方法以Shannon信息熵为基础理论，是目前公认的能准确计算延迟时间的方法之一，在相空间重构中应用广泛，具体算法如下：

已知铰点振动信号的一维时间序列为{xi|i=1，2，…，N}，从中取序列X={xi|i=1，2，…，N-τ}，经延迟时间τ后形成序列Y={xi+τ|i=1，2，…，N-τ}，则对于不同的延迟时间τ，序列X和Y的互信息为

式中：H(X)、H(Y)分别为序列X和Y的 Shannon信息熵；H(X，Y)为两者的联合信息熵；p(xi)为xi在序列X中出现的概率；p(xi+τ)为xi+τ在序列Y中出现的概率；p(xi，xi+τ) 为xi在序列X中出现且xi+τ在序列Y中出现的概率。

取延迟时间-互信息曲线上第一个极小值对应的延迟时间作为相空间重构的最佳延迟时间。

1.2 嵌入维数的计算

在相空间重构的过程中，若m过小，原本相距较远的点在重构相空间中变得非常接近，吸引子发生折叠，无法恢复原吸引子的结构；若m过大，吸引子的几何结构将完全打开，但计算量会增大，且噪声的影响也会增大。本文采用CAO 法［15］确定嵌入维数m，该方法是一种伪近邻算法，算法简便，计算准确，是目前使用较多的算法，具体算法如下：

已知铰点振动信号的一维时间序列为{xi|i=1，2，…，N}，以m为嵌入维数，τ为时间延迟，重构相空间，在m维相空间中得到N-(m-1)τ个相点，其中Xi(m) =(xi，xi+τ，xi+2τ，…，xi+(m-1)τ)为第i个相点，令

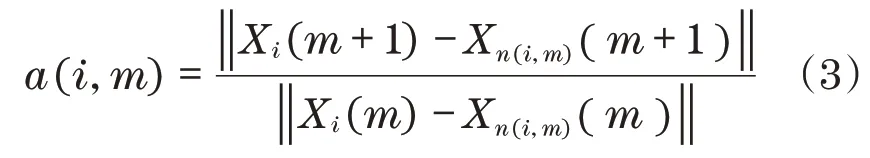
式中：i=1，2，…，N-mτ，Xi(m+1)为在m+1 维相空间中的第i个相点；Xn(i，m)(m)为在m维相空间中Xi(m) 的 最 近 邻 点 ；n(i，m) 为 整 数 ，且 1≤n(i，m) ≤N-mτ；‖ • ‖为相点间的欧氏距离。

可得a(i，m)的均值为

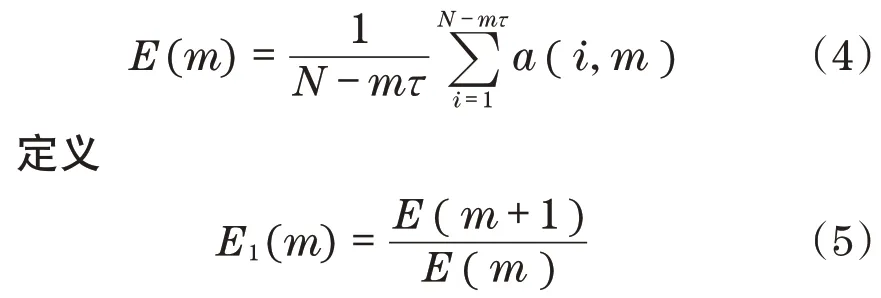
当嵌入维数m大于某值m0时，E1(m)将停止变化，m0则为最佳嵌入维数。由于有时无法判断有限长序列E1(m)究竟是在缓慢变化还是已稳定，通常再结合以下补充判断准则共同确定最佳嵌入维数：

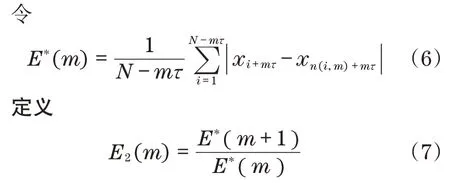
当嵌入维数m大于某值m0时，E1(m)和E2(m)都停止变化，m0则为最佳嵌入维数。

在本文中，当E1(m)呈单调上升趋势且始终大于0.8，并且E2(m)始终在1 附近时，认为E1(m)和E2(m)停止变化。

2 混沌识别技术

运用混沌理论的方法对铰点振动信号进行研究，首先要识别铰点振动信号是否具有混沌特性。目前混沌识别的方法很多，但由于每种方法的考察角度不同，各方法基本都只是从某一个方面来识别混沌，因此，为提高混沌识别的可靠性，通常需要结合多种方法进行识别［16］。本文采用功率谱法和李雅普诺夫指数（Lyapunov Exponent）法分别从定性和定量2 个角度对岸桥铰点振动信号进行混沌识别。

2.1 功率谱分析

功率谱反映了信号功率在频域内的分布情况。研究表明：随机噪声的功率谱曲线在整个频域内连续且相对平坦，没有明显的峰值；包含周期或准周期成分的信号，其功率谱中存在明显的尖峰；具有混沌特性的信号，其功率谱则具有连续性和宽峰的特点［17］。因此，根据功率谱图的分布特点可以识别出信号是否具有混沌特性。

2.2 最大Lyapunov指数

Lyapunov 指数是描述相空间内邻近轨道的平均发散率的物理量，在混沌识别的过程中，通常估计最大Lyapunov 指数。当该值大于零时，则表明系统具有混沌特性，且最大Lyapunov指数越大，相空间轨道发散越快。目前计算最大Lyapunov指数的方法主要有 Wolf 法、Jacobian 法、p-范数法和小数据量法等。其中，由Rosenstein等［18］提出的小数据量法是Wolf 方法的一种改进，有针对小数据组可靠性强、计算量较小、容易操作及精度较高的优点，且相对于其他方法更具有对相空间的嵌入维数、延迟时间、观测噪声等的鲁棒性［19］。因此，本文采用小数据量法计算铰点振动信号的最大Lyapunov指数，具体算法如下：

首先根据前述方法重构相空间，获得重构相空间 中 的 相 点Xi=(xi，xi+τ，xi+2τ，…，xi+(m-1)τ)，i=1，2，…，n，其中，n=N-(m-1)τ，τ为最佳延迟时间，m为最佳嵌入维数。然后对信号进行快速傅里叶变换，运用加权平均法［20］计算信号的平均周期P。根据下式寻找每个相点的最近邻点，并限制短暂分离：

式中：di(0)为第i个相点Xi和其最近邻点Xî的初始距离；‖ • ‖为 相点间的欧氏距离。

根据下式计算信号中每个相点和其最近邻点经过j个演化步长后的距离di(j)：

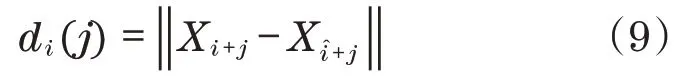
式中：j=1，2，…，T，T为演化长度。

再根据下式对每个演化步长j求出所有相点的lndi(j)的平均值y(j)，得到信号的演化步长-y曲线：

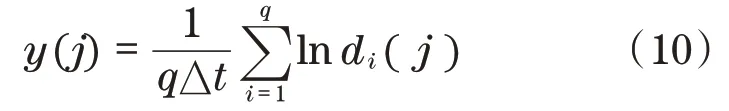
式中：q为非零di(j)的个数；Δt为时间序列的采样时间间隔。

运用最小二乘法对得到的曲线进行直线拟合，所得直线的斜率即为振动信号的最大Lyapunov指数。

3 实例分析

3.1 铰点振动信号采集

本文以上海某集装箱码头4#岸桥作为研究对象，探讨运用混沌理论对岸桥铰点振动信号进行分析的可行性和有效性。信号采集依托上海海事大学研发的Net-CMAS 系统完成，在该岸桥大梁的左右侧铰点处分别设置测点Z5V 和Z6V，在垂向安装振动加速度传感器PCB608A，铰点振动信号的测点位置以及传感器现场布置如图1所示。

图1 铰点振动信号测点位置及传感器现场布置Fig.1 Position of measuring points for vibration signals of hinge points and site layout of sensors

该岸桥铰点区域内的轨道垫板磨损严重，轨道固定螺栓有不同程度的磨损，轨道接头处也出现了裂纹，铰点处的振动冲击不断加剧，而且，现场检查发现左侧铰点区域的磨损情况明显比右侧严重。为防止工况进一步恶化，码头方于2017年2月对该区域进行了修复。

本课题组分别于修复前后对该岸桥进行了铰点冲击测试，每次测试包含2 种情况：①小车重载全速从陆侧出发经过铰点后到达海侧；②小车重载全速从海侧出发经过铰点后到达陆侧。每次测试时左右2 个测点的信号同时采集。为不失一般性，修复前后的测试分别进行4 次，最终获得32 组铰点振动信号，每组信号的采样频率均为4 129 Hz，采样时长均为6 s。为便于对信号进行描述和引用，将信号及其采集工况进行编号，信号的具体工况说明及编号如表1所示。

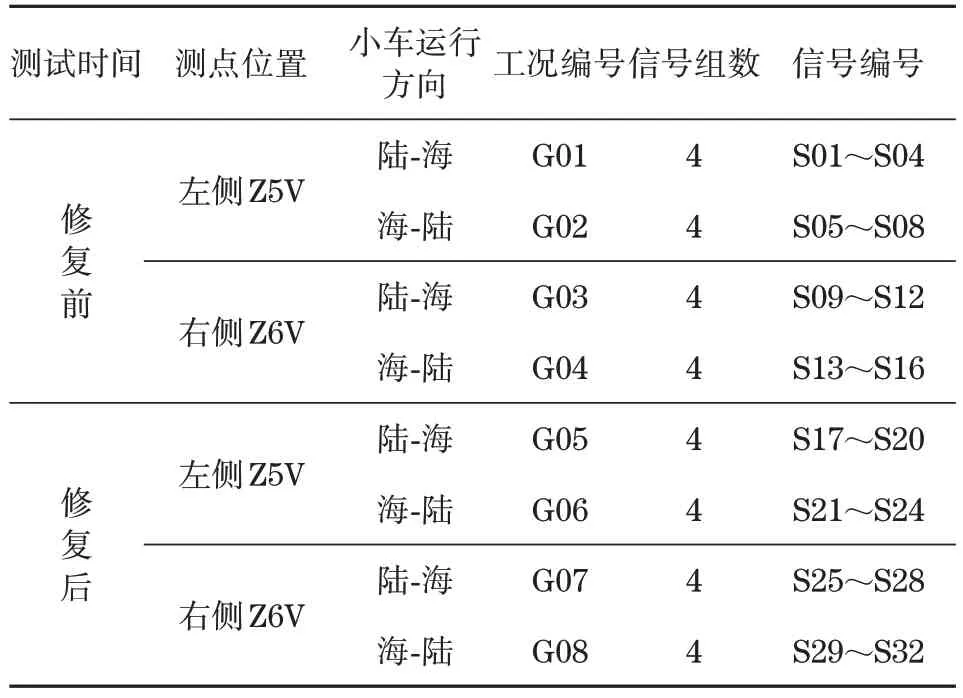
表1 信号的具体工况说明及编号Tab.1 Description of specific working conditions and the number of the signals

3.2 铰点振动信号混沌识别

先运用功率谱法从定性角度识别岸桥铰点振动信号是否具有混沌特性。以铰点区域修复前后同一测点在相同工作状态下的信号S01 和S17 为例，两者的时域曲线图和功率谱如图2所示。

图2 信号S01和S17的时域曲线和功率谱图Fig.2 Time domain curves and power spectra of Signal S01 and Signal S17

由图可见，2 组铰点振动信号的功率谱在整个频域内存在明显的峰值，但峰值与周围的谱线连成一片，具有宽峰的特点，而且在整个频域内功率谱是连续的，说明这2 组信号具有混沌特性。绘制其余各组铰点振动信号的功率谱，发现其余各组信号的功率谱图也具有同样的特点，说明铰点振动信号具有混沌特性。

运用前述小数据量法计算铰点振动信号的最大Lyapunov 指数，从定量的角度进行混沌识别。仍以图2 所示的2 组信号为例，取演化长度T=500，绘制2 组信号的演化步长-y曲线如图3所示。

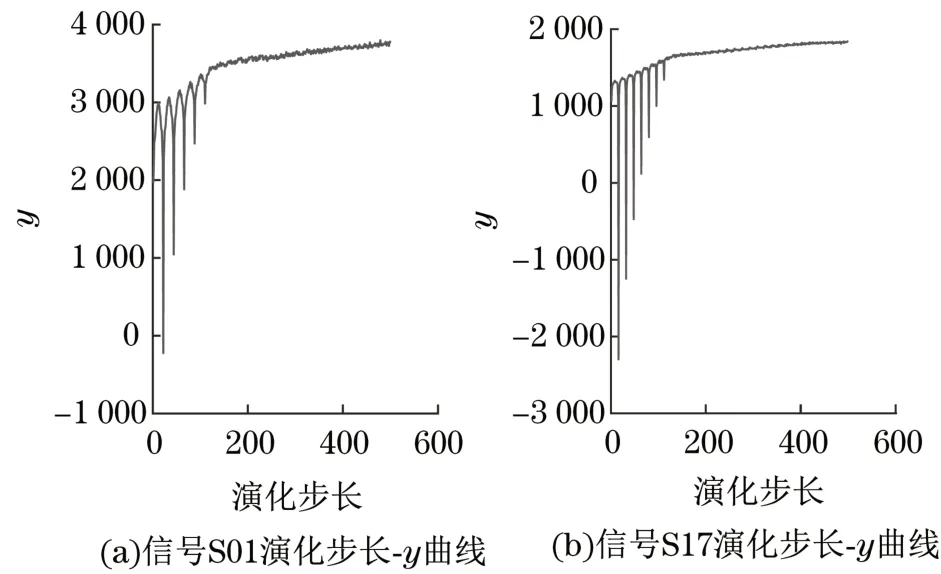
图3 信号S01和S17的演化步长-y曲线Fig.3 Evolution step-y curves of Signal S01 and Signal S17

经直线拟合，得到信号S01 和S17 的最大Lyapunov 指数分别为 1.945 0 和 1.200 9，均大于 0，说明这2 组信号都具有混沌特性。运用同样的方法计算其余各组信号的最大Lyapunov 指数，发现其余各组信号的最大Lyapunov指数也都大于0，进一步说明岸桥铰点振动信号具有混沌特性。

上述定性和定量分析都表明岸桥铰点振动信号具有混沌特性，可见运用混沌理论的方法对岸桥铰点振动信号进行研究是可行的。

3.3 基于混沌特性的铰点工作状态识别

最大Lyapunov指数和混沌吸引子结构特征是混沌理论中用于描述混沌信号的重要特征，下文依据这2个特征，从定量和定性2个角度，对岸桥铰点工作状态进行识别。首先对各组信号进行相空间重构，经计算得各组信号的最佳延迟时间在2~27之间，最佳嵌入维数在3~8 之间。为便于对比，在保证各组信号的吸引子结构都能完全打开的情况下，统一取延迟时间为27，嵌入维数为8。

3.3.1 基于最大Lyapunov指数的状态识别

经过计算得各组信号的最大Lyapunov指数及同种工况的均值如图4所示。

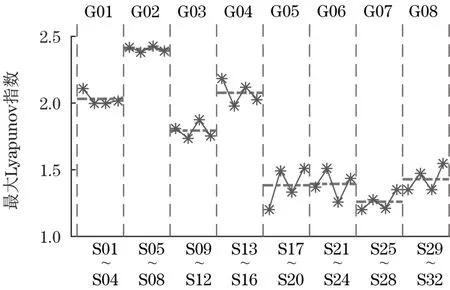
图4 各组信号的最大Lyapunov指数及同种工况的均值Fig.4 The maximum Lyapunov exponent of each signal and the mean value of the exponents under the same working condition

结合图4，从三方面验证运用最大Lyapunov指数区分岸桥铰点工作状态的有效性：

（1）修复前后的铰点振动信号对比。如图4所示，修复前（工况G01~G04）各组信号的最大Lyapunov 指数明显大于修复后（工况G05~G08）各组信号的最大Lyapunov指数，可见，信号的最大Lyapunov 指数成功区分出了铰点修复前后的状态，这也表明，铰点故障程度越深，最大Lyapunov指数就越大。

（2）小车运行方向不同的铰点振动信号对比。分别对比图中 G01 和 G02、G03 和 G04、G05 和 G06以及 G07 和 G08 这 4 对工况的最大 Lyapunov 指数均值，可以看出小车从海侧运行到陆侧时相应工况的最大Lyapunov 指数均值都大于反向运行工况，表明同等条件下，小车从海侧运行到陆侧时产生的振动比反向运行时大，与实际情况相符。可见，通过对比工况的最大Lyapunov指数均值可以依据小车运行方向对铰点振动信号进行分类。

（3）不同侧的铰点振动信号对比。分别对比图中工况对 G01 和 G03 以及工况对 G02 和 G04 的最大Lyapunov 指数均值，可以看出修复前左侧铰点振动信号的最大Lyapunov指数均值明显大于右侧，这与铰点区域修复前左侧铰点区域的磨损情况较右侧更为严重的实际情况相符。进一步对比工况对 G05 和 G07，以及工况对 G06 和 G08 的最大Lyapunov 指数均值，可以看出修复后左右两侧的冲击振动强度虽然仍有差异，但相对修复前，两者间差异明显减小，这与实际的修复效果也是一致的。

上述三方面的对比情况表明，最大Lyapunov指数可以有效区分岸桥铰点的工作状态。

3.3.2 基于混沌吸引子结构特征的状态识别

观察各组铰点振动信号的混沌吸引子发现，各组信号的混沌吸引子的结构在各个平面上的投影均呈现出四角星的形状；在同种工况下，信号的混沌吸引子结构相似，且重复性好，形状、大小、位置几乎相同，而工况不同时，信号的混沌吸引子结构则有不同程度的差异。不同工况下的铰点振动信号的混沌吸引子如表2 所示，囿于篇幅，表中仅列出每种工况下第一组信号的混沌吸引子。

结合表2，同样从三个方面验证运用混沌吸引子的结构特征区分岸桥铰点工作状态的有效性：

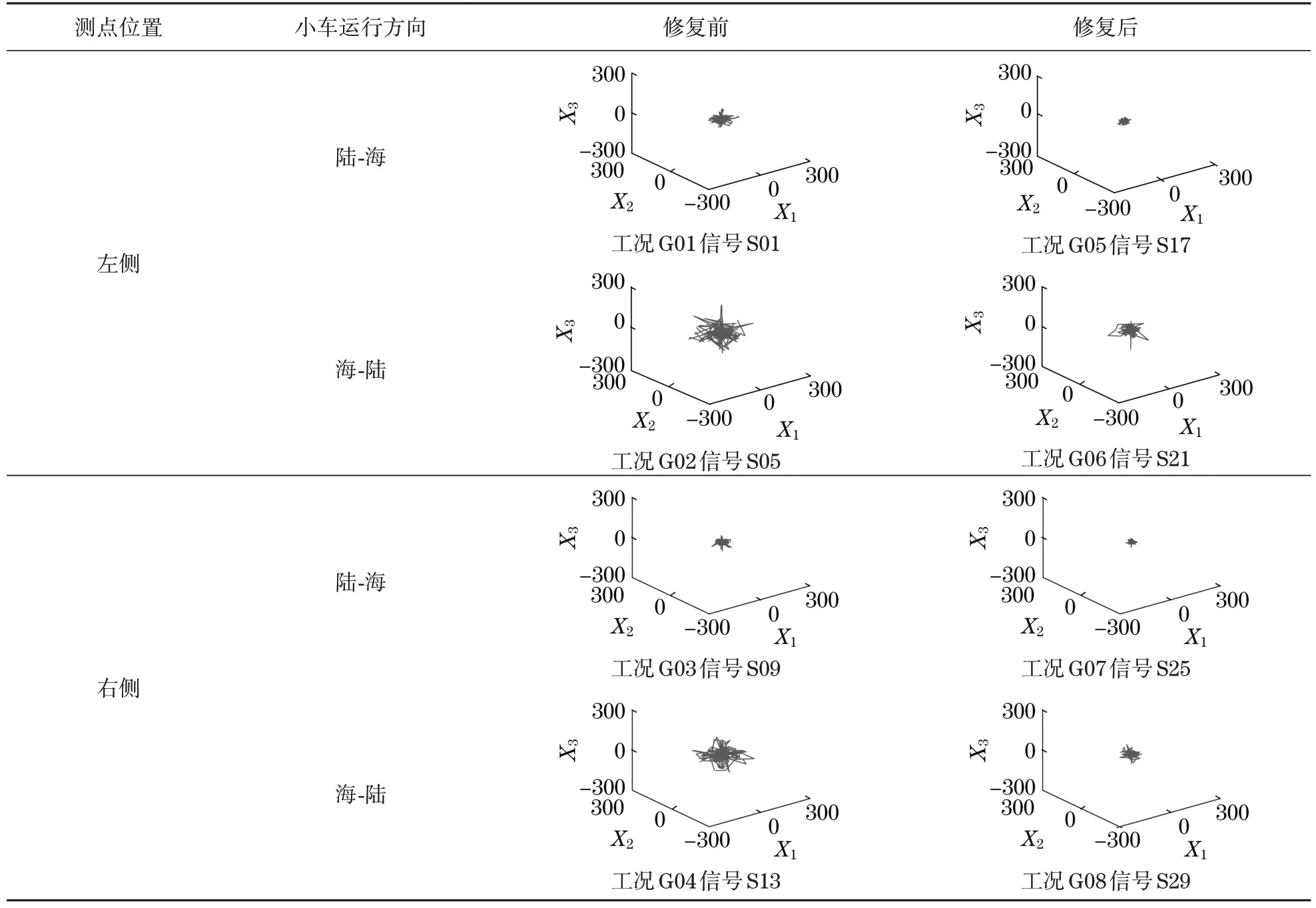
表2 不同工况下的铰点振动信号混沌吸引子Tab.2 Chaotic attractors of vibration signals of hinge points under different working conditions

（1）修复前后的铰点振动信号对比。观察修复前后的信号的混沌吸引子可以看出，在同样的测试条件下，修复后测得的信号的混沌吸引子，轨迹线较修复前的更为集中，体积比修复前的明显减小。可见混沌吸引子的结构特征可以有效区分铰点的状态，铰点的故障程度越深，相应的振动信号的混沌吸引子的轨迹线就越发散，吸引子的体积也越大。

（2）小车运行方向不同的铰点振动信号对比。从上一节的分析可知，通过对比工况的最大Lyapunov 指数均值，可以依据小车运行方向对铰点振动信号进行分类。但当2 种状态的最大Lyapunov 指数均值差异很小时，则可能因为计算精度不够而被误判为同一种状态，如图4 中工况G05和工况G06便存在被误判的可能。对比表2中这2 种工况的信号的混沌吸引子结构特征，却发现两者的混沌吸引子结构明显不同，工况G06的混沌吸引子比工况G05的体积大，而且试图脱离吸引子中心的轨迹也更多，说明在工况G06下铰点区域的振动更强烈。据此可判断在工况G06 下小车运行方向为从海侧到陆侧，在工况G05下小车运行方向为从陆测到海侧，显然与实际情况相符。可见，将混沌吸引子结构特征与最大Lyapunov 指数相结合，能克服单一使用最大Lyapunov 指数进行状态识别的不足，提高状态识别的准确性。

（3）不同侧的铰点振动信号对比。对比表2中工况对 G01 和G03，以及工况对G02 和G04 的信号的混沌吸引子，可以看出修复前左侧信号的混沌吸引子的体积比右侧信号的大，试图脱离吸引子中心的轨迹线也比右侧信号的多，说明左侧铰点振动信号的强度较右侧大，与修复前左侧铰点区域磨损较右侧更严重、振动更强烈的实际情况一致。再对比修复后的工况对G05 和G07，以及工况对G06 和G08 的混沌吸引子，可以看出修复后左右2 侧铰点振动信号的混沌吸引子体积大小较修复前更为接近，表明该次修复后改善了左右2侧铰点区域磨损不一致的情况，这与实际的修复效果一致。

上述分析表明：铰点振动信号混沌吸引子的结构特征也能有效区分岸桥铰点的工作状态，将混沌吸引子结构特征与最大Lyapunov指数相结合能克服单一使用最大Lyapunov指数进行状态识别的不足，提高状态识别的准确性。

4 结论

岸桥铰点振动信号蕴含着丰富的岸桥健康状态信息，鉴于铰点振动信号具有典型的非线性、非平稳特征，本文尝试运用混沌理论的方法对实测岸桥铰点振动信号进行分析，得到以下结论：

（1）岸桥铰点振动信号的功率谱具有连续性和宽峰的特点，且最大Lyapunov指数为正，说明岸桥铰点振动信号具有混沌特性，用混沌理论的方法进行分析是可行的。

（2）同种状态的岸桥铰点振动信号的最大Lyapunov 指数和混沌吸引子结构特征重复性好，而不同状态的铰点振动信号的这2 个特征则有不同程度的差异，特别是混沌吸引子的结构特征差异明显。

（3）将最大Lyapunov 指数和混沌吸引子结构特征结合起来可以准确区分铰点工作状态，说明运用混沌理论的方法对岸桥铰点振动信号进行分析在工程实际中切实有效，可以做进一步研究。