基于响应面分析法的桥式起重机主梁轻量化设计

张亮有，王亚湖，琚 超，程建博，刘孟飞

（太原科技大学机械工程学院，山西太原030024）

起重机广泛应用于车间、仓库、矿山、冶金等场所。由于其自身结构的特点，重型机械的设计为了追求较高的安全性能，往往会采用较大的安全系数。因此，我国的起重机结构比较笨重，体积比较大。针对这一问题，许多学者在对起重机结构优化、轻量化等方面做了大量的研究，在一定程度上推动了起重机的发展。

刘志刚等［1］采用响应面分析法对预弯机进行轻量化设计，优化后预弯机质量减小了8 330 kg。褚艳涛等［2］基于响应面模型对连杆进行轻量化研究，优化后质量比原结构减小了25.41%。潘峰等［3］基于改进的响应面法对车身进行了轻量化，使得整车耐撞性能得到提高的同时实现车身前部结构质量减小21.40%。万宇阳等［4］基于响应面法对挖掘机的动臂进行轻量化设计，在保证结构性能的前提下，动臂质量减小14.70%。本文采用响应面分析法结合有限元分析法对桥式起重机主梁进行轻量化设计，建立主梁质量和结构尺寸参数的优化目标函数，在满足设计和材料的要求下使主梁的质量最小。

1 主梁模型及简化

以QD 30 t、跨度25.5 m、工作A5 级的箱型桥式起重机主梁为研究对象，主梁质量在桥式起重机总 质 量 中 所 占 比 重 最 大［5］。 小 车 质 量Gx=10 500 kg，一根主梁的质量Gz=7 555.1 kg。小车轮距3.6 m，相邻之间的大隔板距离1 450 mm，大隔板厚度6 mm，上下盖板厚度16 mm，腹板厚度6 mm，腹板高1 450 mm［6］。

采用三维建模软件SolidWorks 对主梁模型进行相应的简化，可提高建模的效率，降低网格划分出错的概率，减少运算时间，如忽略主梁中的小隔板、加强筋等对主梁的稳定性、静态刚度和静态强度影响不大的部分［7］。为尽可能反映主梁的实际工况，对主梁进行客观分析和反复建模计算，得出只设置大隔板与实际工况更加贴切。主梁在SolidWorks环境下简化模型如图1所示。

图1 主梁三维模型简图Fig.1 Schematic diagram of the three-dimensional model of the main beam

2 有限元静力学分析

通过SolidWorks 与Workbench 的无缝链接，避免中间格式带来的模型导入错误，将模型导入到Workbench 中，设置起重机主梁的材料参数，模型的材料设置具体参数如表1所示。

表1 材料参数设定Tab.1 Material parameter setting

网格划分的质量对有限元模型的求解精度和速度都有关系，高质量的网格对应高的求解精度和较快的求解速度，主梁的网格划分后产生108 506个单元，212 776个节点。

主梁与端梁通过焊接连在一起，故可在主梁与端梁接触的端面上施加全约束来分析。主梁的自重可以选用标准重力加速度给予考虑。主梁所受的载荷施加在主梁上盖板与小车轨道相接触的区域［8］。轮压区的宽度约为小车行走轨道高度的3倍，这里只考虑最危险的工况即满载小车跨中的位置，选择最大的2 个轮压校核，小车受到的最大静轮压为117 600 N。

主梁应力云图如图2 所示，主梁的最大位移云图如图3 所示。由图可以得出，主梁的最大应力在上盖板与小车接触的轮压处，最大位移则在跨中的位置。 主梁最大应力和最大变形分别为126.52 MPa 和14.213 mm，均远小于主梁的许用挠度和许用应力（31.875 mm 和176 MPa），因此，有较大的优化空间，所以有必要对主梁结构进行优化设计。

图2 主梁的最大应力云图Fig.2 Maximum stress cloud diagram of the main beam

图3 主梁的最大位移云图Fig.3 Maximum displacement cloud map of the main beam

3 轻量化设计

3.1 优化的数学模型

根据设计要求，主梁截面的尺寸参数作为设计变量，最大许用挠度和许用应力为约束条件，质量为目标函数，建立如下优化数学模型［9］：

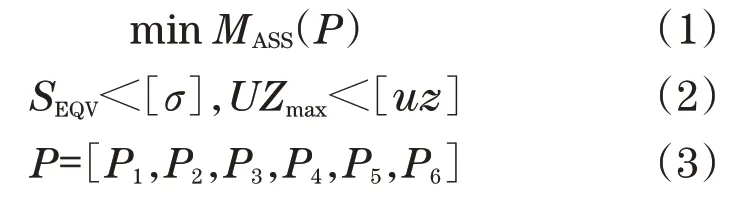
式中：MASS（P）为质量函数；SEQV、UZmax为约束条件；［P1，P2，P3，P4，P5，P6］为设计变量。

3.2 参数设置

根据起重机的工作原理并结合静力学分析得出的结果，将对分析结果影响较大的结构尺寸设为参数，包括上下盖板厚P1和P6，左右腹板厚度P2和P3，主梁腹板高P4，大隔板厚度P5，如图4所示。

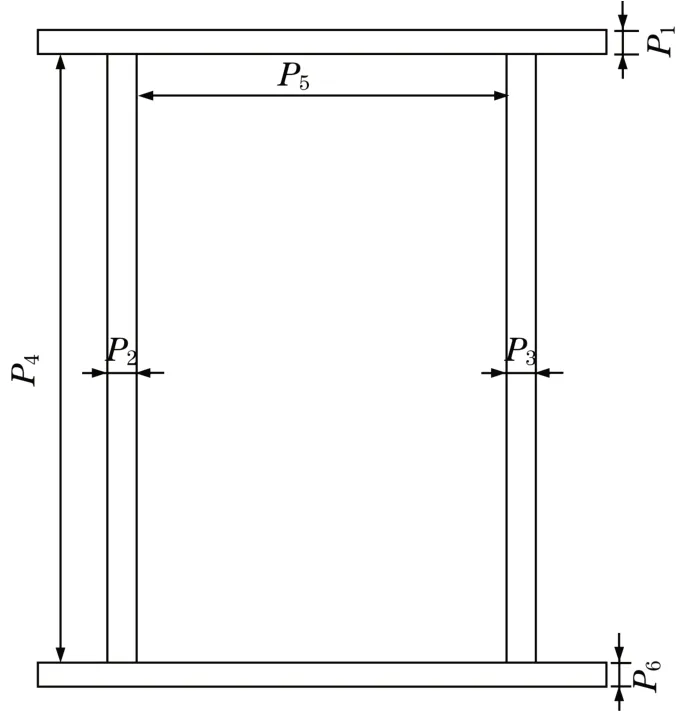
图4 主梁截面Fig.4 Main beam section

3.3 响应面分析

将主梁模型加载到Workbench 环境后，将主梁界面对静态分析结果影响较大的结构尺寸进行参数化设计。将静力学分析得出的最大应力、应变设为参数。参数设置完成后，从工具箱栏Design Exploration 中的Response Surface Optimization模型的优化考虑桥式起重机主梁在满载小车处在跨中的危险工况［10］。P1上限值 22 mm，下限值14 mm；P2上限值8 mm，下限值6 mm；P3上限值8 mm，下限值6 mm；P4上限值1 600 mm，下限值1 300 mm；P5上限值6 mm，下限值4 mm；P6上限值16 mm，下限值6 mm。

尺寸约束设置后，生成不同参数组合的表格数据，然后在实验设计类型栏中选用中心复合实验设计CCD。实验设计方法产生45 组样本点，部分优化数据如图5 所示。为了研究主梁的结构优化问题，需要对响应面进行分析。主梁上盖板厚为P1，腹板高为P4，最大总位移为P8，最大等效压力为P9。P1、P4和P8之间的响应曲面关系如图6 所示。上盖厚度P1、腹板高度P4与最大变形P9的响应面关系如图7 所示。每个输入和输出变量之间的敏感度关系如图8所示。

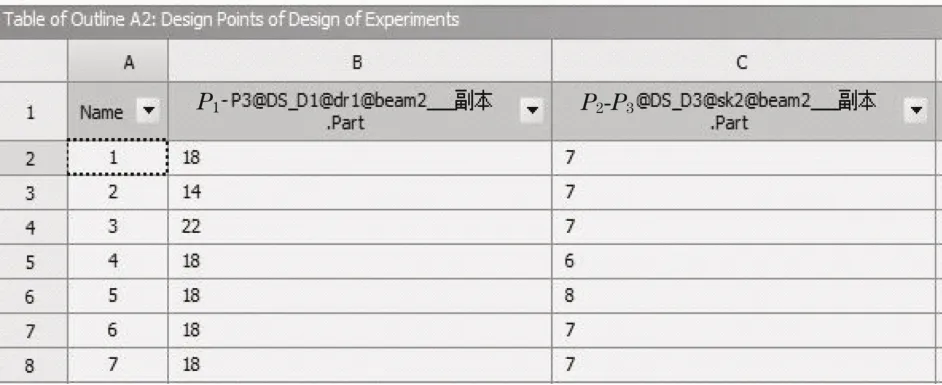
图5 优化数据表Fig.5 Optimize the data table

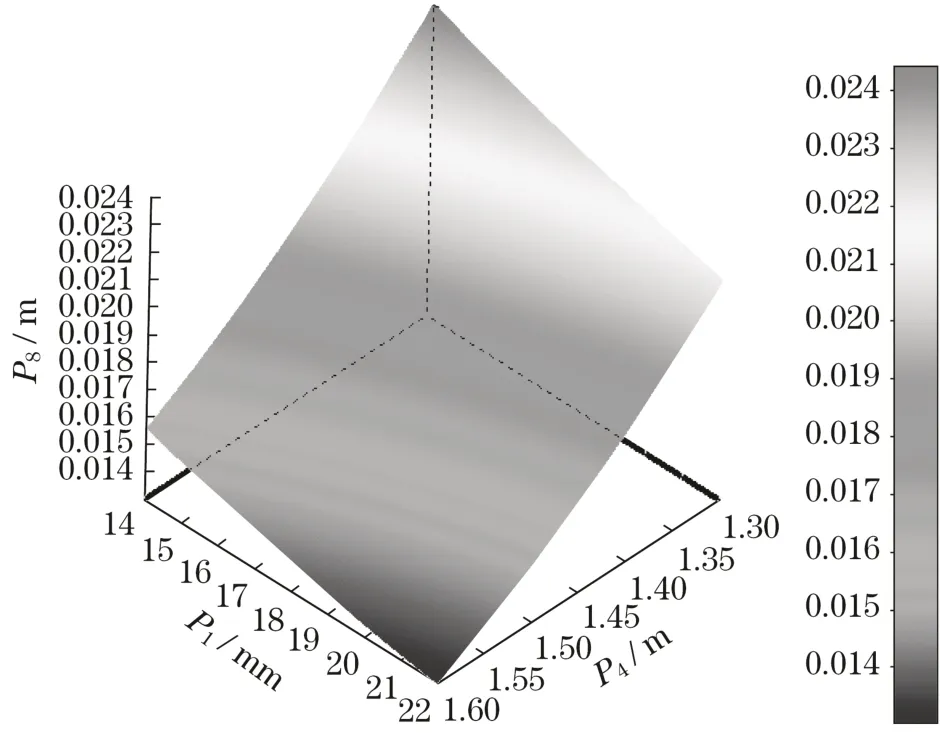
图6 P1和P4对应P8的响应曲面Fig.6 P1 and P4 correspond to the response surface of P8

图7 P1和P4对应P9的响应面Fig.7 P1 and P4 correspond to the response surface of P9

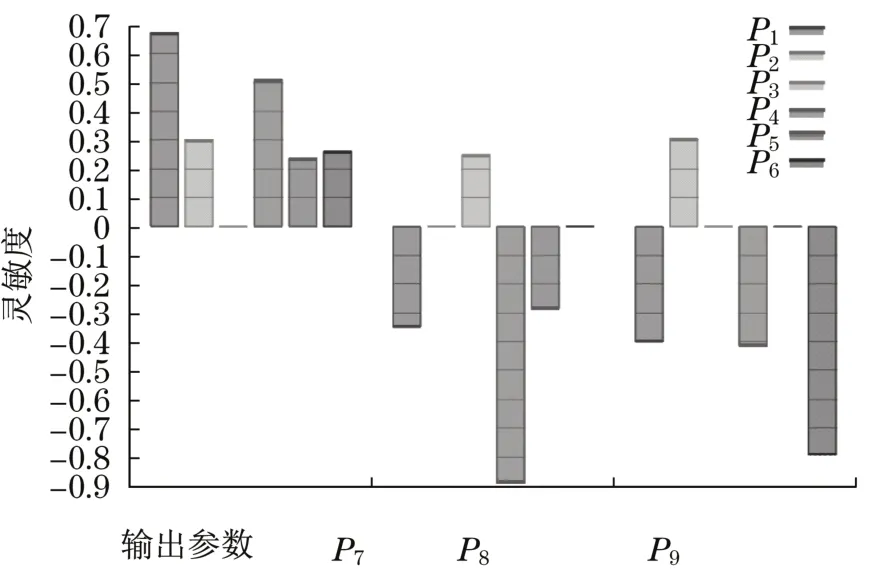
图8 相关参数灵敏度Fig.8 Sensitivity of related parameters

主梁结构优化前的参数与优化圆整后的参数如表2 所示。主梁上盖板的厚度和腹板高对主梁的质量影响较大，与前面得出的响应曲面和灵敏度分析的结果具有一致性。

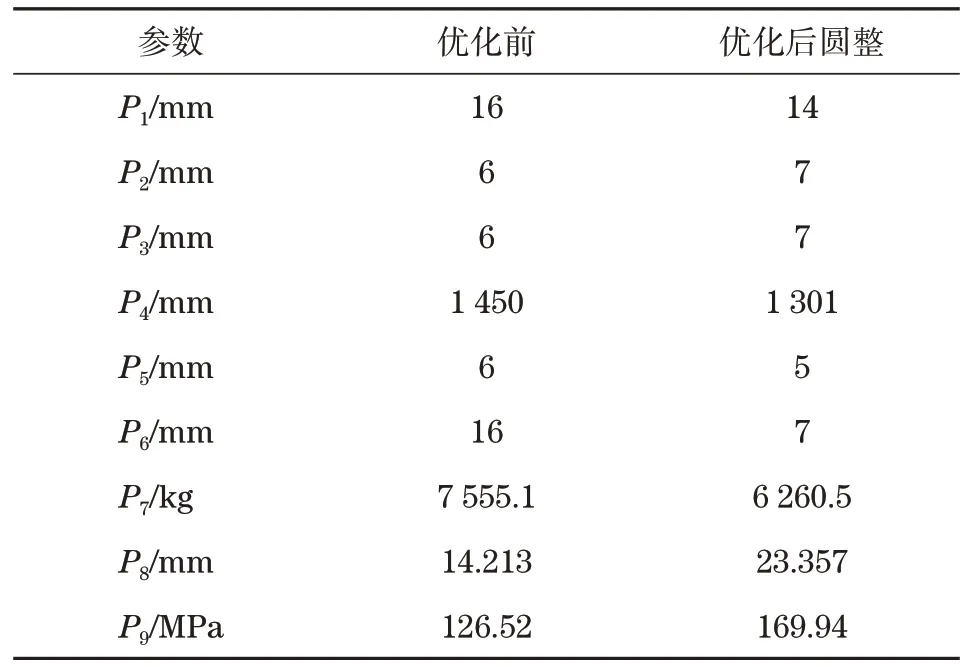
表2 优化前与优化圆整后的参数Tab.2 Parameters before optimization and after optimization rounding

4 结语

通过三维建模软件SolidWorks 对主梁简化建模，在Workbench 中对其进行静力学分析，将对主梁应力影响较大的结构尺寸设为参数，以轻量化为目标进行响应面优化设计。在满足刚度和强度的要求下取得了主梁质量减小17.14%，达到了起重机主梁结构简化、质量减小、节约成本的目的，同时也提供了一种作为参考的主梁优化设计方法。