基于随机生存森林的企业财务危机研究
2021-12-22肖叶宇
肖叶宇,张 闪
(1.吉林大学数学学院,吉林 长春 130012) (2.南京财经大学应用数学学院,江苏 南京 210023)
近年来随着我国证券市场的高速发展,上市公司的财务危机已成为投资者所关心的重要问题. 一旦上市公司因连续亏损或财务状况异常而被特别处理(ST),则该公司会被认为陷入财务危机,其投资者也会受到负面影响. 故而建立有效的企业财务预警模型,让上市公司及早发现危机并采取措施,对各利益相关方都有积极的意义.
目前我国的财务危机研究在统计方法上主要可分为两大类,一是将其看做二分类问题即公司是否被ST,所用模型包括判别分析模型、Logistic模型、支持向量机[1]等. 二是将生物统计里的生存分析理论引入财务危机问题中,由于生存分析模型可以处理删失数据,并给出研究对象各时间点的生存概率,所以将生存分析应用到财务危机预警中有很强的现实意义.
前人在财务危机研究中采用的生存分析模型多以Cox模型为主[2-3],但Cox模型依赖于比例风险假设,而且在确定变量的非线性影响、识别交互作用上都有局限性. 随机生存森林是在随机森林模型的基础上提出的一种可以分析右删失数据的集成树方法,它继承了随机森林的优点,故而可以克服这些局限,并且在高维数据下显著优于其它生存分析方法.
本文首先采用随机生存森林模型研究财务危机,所研究样本为沪深两市A股制造业上市公司,得到随机生存森林模型下各财务指标的重要性,然后比较随机生存森林和3种Cox模型的预测精度,最后结合模型结果给出分析与建议.
1 随机生存森林与企业财务危机
生存分析是医学领域研究生存时间的主要方法,在生存分析中生存时间的主要刻画方式有:生存函数和风险函数. 生存函数定义为:
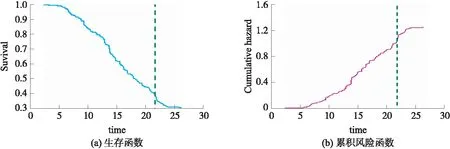
S(t)=P(T>t),0 (1) 表示为生存时间T超过t的概率,其中T为非负随机变量. 风险函数定义为: (2) 本文将公司的首次上市作为生存时间的起始事件,以公司被ST作为结局事件,二者间隔的时间为该公司的生存时间. 若某公司在观测结束时还未被ST便被视为删失个体,其生存时间为右删失数据. 若某公司被ST则为失效个体,其生存时间为完全数据. 首先使用Bootstrap重抽样在原始数据中抽取B个Bootstrap样本,其中每个Bootstrap样本的数据量与原始数据相同,由于是有放回抽样,故原始数据中约有37%的数据不会出现在一个Bootstrap样本里[6],这部分数据称为该Bootstrap样本的袋外数据. 在每个Bootstrap样本上都建立二元递归生存树模型,一棵树生长的过程中,在每个内部节点需要分裂时都随机选择p个候选变量(假设原有变量P个,P>p). 使用最大化子节点之间生存差异的候选变量对节点进行分裂,本文选择Log-rank统计量来刻画生存差异,Log-rank统计量的绝对值越大生存差异越大. 生存树生长为完整大小,不采取任何剪枝,每个节点必须包含最少d0个拥有不同生存时间的ST公司,当不满足该条件无法生成子节点时终止生长. 那么这些最后的节点就被称为终节点,记为H.设h为树的一个终节点,(T1,h,δ1,h),…,(Tn(h),h,δn(h),h)为终节点h中公司的生存时间和删失信息,对公司i而言,δi,h=1表示在Ti,h被ST,δi,h=0表示在Ti,h发生右删失.设t1,h (3) 注意到终节点h中的所有公司共用一个累积风险函数估计,那么一棵树的累积风险函数就可以写为: (4) 式中,xi代表公司i的协变量,h∈H. 式(4)是一棵生存树的累积风险函数,而随机生存森林的累积风险函数需要计算生存树的平均,包括袋外数据估计和Bootstrap估计. 每棵生存树都是使用独立的Bootstrap样本建立的,共有B个样本.则公司i的累积风险函数袋外数据估计为: (5) (6) (1)一致性指数(C-index) 随机生存森林使用C-index计算预测误差. C-index估计了在随机选择的一对个体中,拥有更差预测结果的个体最先发生失效的概率,而且不同于其他衡量指标,它考虑到了删失的情况. C-index的计算步骤如下: Step 2. 删掉样本配对中企业生存时间较短的公司是非ST公司的配对,删掉样本配对中企业生存时间相同且都是非ST公司的配对. 记剩下的有效配对数为P. Step 3. 在有效配对里,在Ti≠Tj时,若有更短的生存时间的企业有更差的预测结果则记为1,若预测结果相同则记为0.5;当Ti=Tj且两个企业都是ST公司时,若预测结果相同记为1,否则记为0.5;当Ti=Tj且只有一个是非ST公司时,若ST公司有更差的预测结果则记为1,否则记为0.5. 将上述有效配对的结果求和,记为C. 袋外预测误差PE则被定义为:PE=1-C. (2)Brier score与IBS 在生存分析中还有几种指标被用来评估模型:带有逆概率删失加权的Brier score和Integrated Brier score(IBS). 带有逆概率删失加权的Brier score定义为: (7) (8) 由上式可知Brier score是时间的函数,它的总体度量是Integrated Brier score: (9) 式中,τ>0,τ为样本中最大生存时间,用以总结测试集中的预测误差[9-10]. 变量重要性(VIMP)筛选变量:为计算变量x的VIMP,将袋外数据代入袋内数据生成的生存树中. 当遇到使用变量x的分割时,随机分配一个子节点. 每个袋外个体的累积风险函数将被重新计算并取平均值.x的VIMP等于使用随机x分配获得的袋外预测误差减去原始的袋外预测误差. VIMP值越大表示该变量具有预测能力,而零或负值表示这是非预测变量[7]. 通过计算变量的最小深度来筛选变量:变量的最小深度为从根节点到该变量最近的极大子树根节点的距离. 对于随机生存森林,计算每棵树下变量的最小深度,然后取平均. 最小深度越小则该变量对预测的影响越大[11]. (1)样本选取 本文研究观测期为公司首次上市到2020年12月31日,生存时间以年为单位. 研究样本来自沪深两市A股制造业上市公司,总计1 606家,其中ST公司306家,在观测期内未被ST的公司1 300家. 此外由于我国证券交易所多因连续两年亏损而对上市公司实施特别处理,故而为使模型具有预测性,若公司在T年被ST或删失,则选取该公司T-3年的指标来进行建模[12]. (2)财务指标初选 在财务指标的选取上,本文结合前人研究基础,从公司的偿债能力、比率结构、经营能力、盈利能力、现金流能力、风险水平、发展能力、每股指标、相对价值指标、股权集中度这10个方面出发,共选取50个指标作为初选财务指标,具体见表1. 同时由于部分公司的指标存在数据缺失,本文使用随机生存森林中的自适应树插值进行数据补全[7]. 表1 财务指标初选Table 1 Primary selection of financial indicators 通过五折交叉验证比较各参数选择下的预测误差,随机生存森林模型参数设置为:节点最小ST公司数为10,节点分裂时候选变量数为10,森林中有1 000棵树. 随后在此基础上计算变量最小深度和VIMP,其中VIMP为100次试验后取平均. 于是得到这两种重要性度量下最有预测性的10个变量,如表2所示. 表2 两种度量下变量重要性排名Table 2 Variable importance ranking under two measures 由表2可知,两种度量下重要性排名前10的变量基本相同,只是从第4位后顺序有所改变. 值得注意的是不管是最小深度还是VIMP,营业收入增长率和息税前利润都明显比其他变量更重要. 最重要的财务指标是营业收入增长率,它反映的是企业营业收入增长的比率,是评价企业发展能力和成长状况的重要指标,它的值越大表示对企业盈利有正面影响,则发生财务危机的可能性越低. 排名第2的是息税前利润,究其原因,它是扣除所得税和财务费用前的利润,是企业真实的经营利润,故而是企业盈利能力的直观体现. 本文采用C-index、Brier score和IBS 3种评价指标衡量随机生存森林(RSF)在企业财务危机中的预测性能,其中C-index越大模型预测性能越好,而Brier score和IBS越小预测性能越好. 本文将随机生存森林与Cox模型、后向逐步Cox模型和Lasso-Cox模型进行对比. 将原始数据集按7:3的比例随机划分为训练集与测试集,分别在训练集和测试集上计算C-index,并重复100次试验得到结果,如图1所示. 图1 4种模型在训练集(左)和测试集(右)上的C-indexFig.1 C-index of the four models on the training set(left)and test set(right) 由图1可知,在训练集上随机生存森林的C-index(中位数为0.870)要优于Cox(0.858)、后向逐步Cox(0.836)和Lasso-Cox(0.846). 在测试集上随机生存森林的预测性能优势更加明显,C-index中位数为 0.859,而Cox模型为0.815,后向逐步Cox为0.812,Lasso-Cox为0.814. 为计算4个模型的Brier score,对原始样本进行100次Bootstrap重抽样,对每个Bootstrap样本在袋内数据上训练模型,使用袋外数据计算Brier score,最后取100次的平均. 由于原始样本中公司的最大生存时间约为27年,故而在计算Brier score时时间设为0到27年. 如图2 所示,在绝大部分时间点上随机生存森林的Brier score都要小于3种Cox模型,因此随机生存森林的预测效果最好. 图2 4种模型的Brier scoreFig.2 Brier score of the four models 同时使用Integrated Brier score总结测试集中的预测误差,如表3所示,随机生存森林的IBS是最低的,即预测效果最好. 表3 4种模型的Integrated Brier scoreTable 3 Integrated Brier score of the four models 为了说明随机生存森林在财务危机问题上的预测性,本文选取股票代码为600866的公司进行分析. 该公司于1994年上市,2016年被ST,生存时间约为21.7年. 将该个体放入已训练好的随机生存森林模型中,计算其生存函数和累积风险函数,如图3所示. 图3 公司的生存函数(左)及累积风险函数(右)Fig.3 Survival function(left)and cumulative hazard function(right)of a company 图3绿色虚线横坐标为该公司被ST的时间. 从图3可以看出该公司在上市20年后生存概率已不到40%,更重要的是在上市21年左右该公司的累积风险函数陡升,也就是说这一时间段风险函数很大即被ST的概率极大,这一结论和该公司在上市21.7年后被ST的事实相吻合. 所以基于随机生存森林,根据公司的财务指标可以计算其生存函数和累积风险函数,从而判断该公司被ST的风险. 本文以沪深两市A股制造业上市公司为研究样本,从公司的偿债能力等方面初选50个财务指标,将随机生存森林模型引入企业财务危机研究中. 通过计算变量最小深度和VIMP得到两种度量下重要性排名前10的变量,发现前4位完全相同,分别是营业收入增长率、息税前利润、应收账款周转率和每股未分配利润,其中营业收入增长率和息税前利润对财务危机的影响最大,后6位变量基本相同只是顺序不同,所以公司若想对财务危机做出预警,需要重点关注这些财务指标. 本文将随机生存森林与Cox模型、后向逐步Cox模型和Lasso-Cox模型进行对比. 通过计算C-index、Brier score和IBS 3种模型预测评价指标,发现随机生存森林要优于3种Cox模型. 此外在随机生存森林模型下,根据公司的财务指标计算其生存函数和累积风险函数,从而得到财务危机的动态时点预测. 证券交易所可以据此随时评估公司的财务危机,必要时给公司预警,敦促其采取相应措施改善经营管理,故而将随机生存森林应用到财务危机预警中是可行的,且有很强的现实意义.
1.1 随机生存森林模型
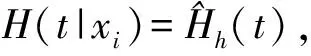

1.2 模型评价指标




1.3 变量选择方法
2 实证分析
2.1 数据描述

2.2 变量重要性

2.3 模型预测比较



2.4 个体分析
3 结论
