多无人系统跟踪与编队的自主式预测控制算法
2021-12-22曹越,王鹏,齐薇
曹 越,王 鹏,齐 薇
(空军工程大学信息与导航学院,西安,710077)
近年来,科技的进步推动了无人系统(如无人机、无人车、无人船/艇)迅猛发展。由多个无人系统基于相互间的交互协同组成一个编队(如无人机群[1]、无人车队[2]、无人船/艇队[3]),可以实现无人系统执行任务能力的质的提升。在多无人系统执行任务的过程中,组成指定队形来对目标进行跟踪(即多无人系统跟踪与编队)是一种常见的应用形式,已广泛地体现在军事和民用等领域(如战场目标侦察打击、毁伤效果评估、协同运输、搜索救援等)中[4]。而相应的多无人系统跟踪与编队问题也已成为了当前的研究热点,备受国内外研究机构与相关学者的重点关注[5-11]。
目前,针对多无人系统的跟踪与编队问题,已涌现出了许多成熟的控制方法,也促生了许多新的控制思路及相应的控制策略,其中多以分布式控制方式(即将整个无人系统的跟踪与编队问题分解成由各无人系统独立解决的控制子问题)为主[6-8],例如文献[6]采用的领航者-跟随者法、文献[7]利用的李雅普诺夫理论、文献[8]采用的滑模控制等等。以上方法相对忽略了无人系统的一些性能要求,而且无法解决一些具有物理约束的实际问题。
预测控制是一种与上述策略不同的控制方法,其控制输入一般通过滚动求解一个涉及未来输入、输出(或状态变量)的有限时域约束优化问题来计算获得,而通过在优化问题中设计合适的目标代价函数来反映控制性能,并对未来输入、输出(或状态变量)加以约束限制,使得预测控制具备了优化控制性能与处理物理约束的特殊能力,也因此成为解决多无人系统跟踪与编队问题的一类针对性方法。目前,针对无人系统跟踪与编队问题开展分布式预测控制研究需要重点解决以下难题:首先为各无人系统构造能够保证其运动控制稳定性的(鲁棒)正定不变集,然后在此基础上设计具有递归可行性保证的分布式控制实施算法[7-10]。
针对多无人系统跟踪与编队问题,现有的分布式预测控制研究均需要满足1个条件:假设跟踪目标时所形成的队形与编队指定的队形一致且不违反无人系统的物理约束[8-11]。然而,在无人系统执行实际任务时,这一前提条件往往不容易满足(如跟踪目标因约束影响而不可实现、编队因障碍影响而不可保持等)。考虑以上实际情况,本文借鉴文献[12]“在跟踪预测控制中引入人工规划目标”的思路,通过在目标代价函数中引入规划目标的方式,解决了跟踪与编队控制目标不一致的问题;进一步通过在控制优化问题中附加规划目标约束的方式,确保规划的目标具有可实现性;最终基于预测控制方法为各无人系统构造出具有递归可行性保证的控制优化问题并给出了相应的控制实施算法。
主要符号
Na多无人系统中无人系统的个数
Na′ 多无人系统的指标集合,即Na′={1,2,…,Na}
Ni无人系统i的邻居集合
Xi无人系统i的状态可容许集合
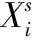
Ui无人系统i的控制输入可容许集合
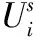
Rnn维的几何空间
Rm×nm×n维的实数矩阵集合
I适维的单位矩阵
Inn维的单位矩阵
0nn维的零矩阵
01×n1×n维的零向量
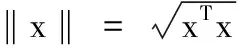
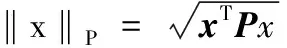
x(t|k)k时刻对k+t时刻状态x(k+t)的预测
N预测时域长度
N整数集合{0,1,2,…,N-1}
N+整数集合{0,1,…,N}
N-整数集合{1,2,…,N-1}
1 问题概述
考虑由Na无人系统所组成的多无人系统,动态方程为:
xi(k+1)=Aixi(k)+Biui(k),i∈Na′
(1)
式中:xi(k)=[pi(k);vi(k)]∈R2n与ui(k)∈Rm分别为无人系统i的状态与控制输入;pi(k)∈Rn与vi(k)∈Rn分别为无人系统i的位置与速度。
在每个无人系统的控制过程中,其状态与输入必须满足以下约束:
(2)
(3)
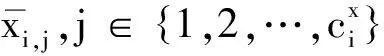
注:式(2)与式(3)是状态与输入约束的通用描述形式,选择状态约束参数Φi,j=[In,0n](或Φi,j=[0n,In])即可描述对无人系统i的位置(或速度)约束,而选择Φi,j=[01×(s-1),1,01×(n-s)]即可描述对无人系统i的第s维状态约束。选择类似形式的输入约束参数Ψi,l即可对不同的输入约束进行描述。
被跟踪目标r为一个虚拟的无人系统,其动态方程为:
xr(k+1)=Arxr(k)+Brur(k)
(4)
式中:xr(k)=[pr(k);vr(k)]∈R2n与ur(k)∈Rm分别为目标r的状态与控制输入;pr(k)∈Rn与vr(k)∈Rn分别为目标r的位置与速度。
本文旨在控制多无人系统跟踪到根据目标r所指定的位置,并形成指定的编队队形,即:

(5)

(6)
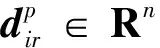
根据以上指定的控制目标,可以为各无人系统i生成目标代价函数:
Ji(xir,uir,xi•,k)=
(7)

注:对于式(5)与式(6)中所指定的控制目标,现有研究成果均要求满足跟踪与编队一致的条件,即
(8)
当该条件不满足时,式(7)中的跟踪目标代价与编队目标代价无法同时趋于零,即无法同时实现跟踪与编队。
本文针对一致性条件(8)不满足的情况,研究更为通用的跟踪与编队控制算法。
2 自主式预测控制算法

通常,各无人系统i利用其上一时刻的真实预测信息来构造当前时刻的假设预测信息,即:
(9)
根据假设预测状态(9),可得相应的状态编队预测偏差:
2.1 目标代价函数重规划
在无人系统执行跟踪与编队的实际任务时,跟踪目标所形成的队形与编队指定的队形往往存在不一致,为了解决这一问题,本文通过为各无人系统重新规划控制目标来对目标代价函数进行设计。

(10)

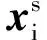
(11)

根据以上所构造的目标代价可知,令规划目标代价(10)最小,可实现对给定跟踪与编队之间的平衡;而令控制目标代价(11)越小,各无人系统对规划目标的收敛性越高。因此,将以上两项目标代价合并,为各无人系统设计出最终的目标代价函数:
(12)
2.2 规划目标的约束设计
在实际问题中,控制目标可能受到环境、无人系统性能等因素影响而不可实现,为了保证规划控制目标的可实现性,本小节对规划的控制目标进行相应的约束设计。
(13)
(14)
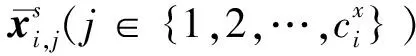

(15)
2.3 无人系统的终端约束设计
根据预测控制的常规方法,需要为各无人系统设计“三要素”(终端代价函数、终端约束集合与终端控制律)[13]。本文借鉴文献[11]设计终端约束的思路为各个无人系统i设计实时的终端约束如下:
(16)
(17)
(18)
(19)

(20)
2.4 控制优化问题构造与控制实施算法设计
对以上设计的代价函数与相关约束进行整合,可为各个无人系统i构造控制优化问题如下:
(21)
s.t.
xi(0|k)=xi(k)
(22)
xi(t+1|k)=Aixi(t|k)+Biui(t|k),t∈N
(23)
xi(t|k)∈Xi,t∈N-
(24)
ui(t|k)∈Ui,t∈N
(25)
(26)
(27)
(28)
(29)
相应的自主式预测控制实施算法设计如下:
2.4.1 离线设置
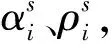
2.4.2 在线实施
在每个在线时刻k≥0,各无人系统i执行以下步骤:
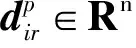
3 优化问题的LMI描述
为了便于对优化问题(21)~(29)进行求解,本节给出一系列变换步骤来将该优化问题转化成LMI形式,具体步骤如下:
1)应用舒尔补引理,预测时域内无人系统i的状态约束(24)与输入约束(25)分别等价于LMI:
(30)
(31)
2)应用舒尔补引理,预测时域内规划目标的状态约束(28)与输入约束(29)分别等价于LMI:
(32)
(33)
3)终端约束(26)中的约束条件(16)~(19)可分别由以下条件保证:
(34)
(Ai+BiKi(k))TPi(k)(Ai+BiKi(k))-
(35)
(36)
(37)
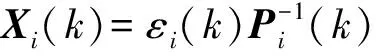
(38)
(39)
(40)
(41)
4)对目标代价函数(21)进行拆分,令:
(42)
(43)
(44)
应用舒尔补引理,式(42)~(44)可分别等价于LMI:
(45)
(46)
(47)
其中:

j,…,l∈Ni
将式(34)与(42)~(44)代入目标代价函数(21),可得其上界:
(48)
5)优化问题(21)~(29),可等价地转化为以下LMI形式的优化问题:
(49)
s.t. (30)~(33),(38)~(41),(45)~(47)
注:约束(22)表示无人系统i在初始时刻的预测值,无需转化为LMI形式;约束(23)与(27)已经分别包含在约束(24)与(28)转化为LMI形式的过程中,无需再单独转化。
4 仿真验证
本文通过一个仿真实例来验证自主式预测控制算法的有效性。考虑一个由3个无人系统组成的多无人系统,各个无人系统的动态方程为:
i∈Na′
(50)
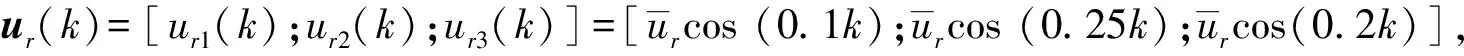
多无人系统指定的状态跟踪与编队偏差向量为:
给定跟踪与编队的权重参数为αi=1、ρi=0.5、βi=0.1,i∈Na′。在控制过程中,无人系统需要满足以下物理约束:
(51)
(52)

设定规划目标的速度与输入约束为:
(53)
(54)

在实施自主式预测控制实施算法中,利用MATLAB中的LMI工具箱(采用“mincx”命令)来求解优化问题。在整个仿真过程中,各个无人系统的优化问题均可求出最优解。仿真结果见图1~3。
从图1可以看出,各无人系统与规划目标的位置轨迹最终重合在一起,多无人系统最终成功地跟踪到了目标,各无人系统最终所形成的队形介于跟踪队形与编队队形之间。以上结果显示:各无人系统能够收敛到规划目标,而通过引入规划控制目标并对目标代价函数进行重新设计解决了跟踪与编队之间的不一致问题。

图1 各无人系统、规划目标与被跟踪目标的位置轨迹以及跟踪与编队的队形图

从图2可以看出,在k=20时,各无人系统便收敛到了规划目标。在k=30时,所有无人系统都已经跟踪上了被跟踪目标。在整个跟踪与编队的过程中,各个无人系统的状态以及规划目标的状态均能够满足指定的状态约束。

图2 各无人系统速度、规划速度与被跟踪目标速度的2-范数
从图3可以看出,在整个多无人系统进行跟踪与编队的过程中,各系统的输入以及规划目标的输入均未违反相应的输入约束,且最终均收敛到被跟踪目标的输入。
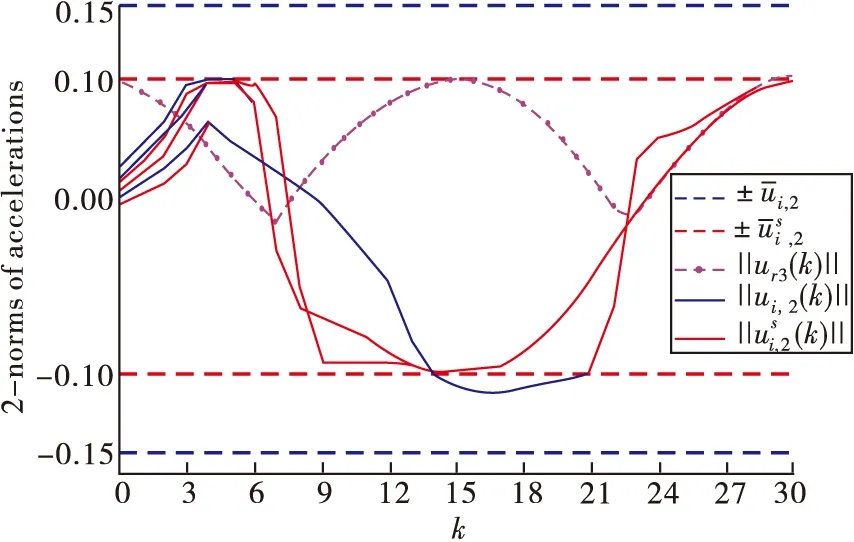
图3 各无人系统输入、规划目标输入与参考目标输入
5 结语
本文针对多无人系统的跟踪与编队问题设计了自主式预测控制算法,通过规划出一致、可实现的控制目标并令整个多无人系统实现该目标,最终解决多无人系统跟踪与编队控制目标不一致及不可实现的问题。本文的跟踪与编队控制算法设计均从单个无人系统自主进行跟踪与组成编队的角度出发,构造的控制优化问题也是由各无人系统独立求解,因此所给出的控制实施算法称为自主式预测控制算法,该算法可以拓展应用于由大规模无人系统所组成的无人集群进行动态编队与拆分重组等问题,具有较高的应用价值。下一步将基于该算法,考虑由大规模无人系统所组成的无人集群避障的需求,解决其进行动态编队与拆分重组等问题。
