基于模糊神经网络的无人机实时避障算法
2021-12-22吕智虎梁晓龙任宝祥张佳强侯岳奇
吕智虎,梁晓龙,任宝祥,李 哲,张佳强,齐 铎,侯岳奇
(1.空军工程大学空管领航学院,西安,710051; 2.陕西省电子信息系统综合集成重点实验室,西安,710051)
无人机具有隐蔽性好、机动性强、成本较低等特点,随着无人机应用领域不断拓展,所处的飞行环境也更加复杂,提高无人机的自主避障能力成为确保任务完成的必要条件[1]。
目前避障算法主要包括势场法[2]、基于图论的算法[3]和智能优化算法[4]。基于图论的避障算法主要有A*算法[5]、D*算法[6]、Voronoi图法[7]等。智能优化算法主要包括遗传算法[8]、蚁群算法[9]、人工蜂群算法[10]、粒子群算法[11]等。当前的无人机避障方法大部分是在障碍物信息已知的条件下进行全局路径预规划,对有碰撞风险的路径进行重规划从而实现避障要求。而在环境中障碍物信息未知的情况下,无人机难以进行全局路径规划,需要无人机能够实时探测并规划避障路径。
针对未知环境中的无人机避障问题,文献[12]提出了一种改进人工势场路径规划算法,实现了未知环境中对静态、动态障碍物的规避,但其避障路径中存在冗余路径。文献[13]提出一种多层双向A*算法,使智能体可以在复杂环境中实时规避突发障碍,但该算法仅适用于少量存在未知障碍物的情况。文献[14]将模糊神经网络应用于无人机电力巡检,无人机能够沿预设路径飞行并规避未知障碍物,但没有利用无人机运动方向与障碍物的角度信息,增加避障路径。
模糊神经网络能够结合已有的避障规则与障碍物特征,通过训练优化模糊控制器的参数,使无人机在障碍物信息未知的环境中依然能够实现避障[15]。
本文首先对模糊控制器的输入变量、输出变量以及初始隶属度函数进行设计,优化了模糊控制器的输入变量;其次利用模糊控制器得到无人机避障的理想路径,从该路径中提取避障过程中无人机运动状态、与障碍物位置关系的数据生成训练数据集,用于训练模糊神经网络;最后将训练后的模糊神经网络在新的未知环境中进行测试验证。
1 无人机实时避障问题建模
1.1 问题描述
在障碍物信息未知的室内飞行区域中,给定起始点O与目标点E,在飞行过程中无人机能够主动探测环境中障碍物信息,并对障碍物进行实时规避,最终安全抵达目标点,如图1所示。由于室内环境较为狭窄,因此选用低速微型无人机。
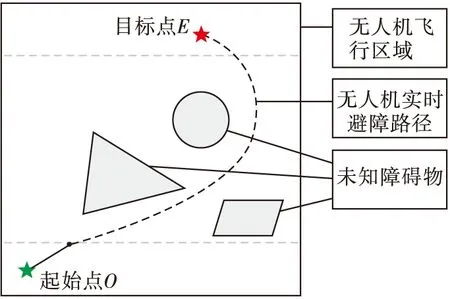
图1 避障环境模型
1.2 模型建立
1.2.1 传感器模型
激光雷达能够测得目标距离、方位甚至形状等参数,具有测量精度高、探测范围大以及结构简单等优点,在避障和建图中较为常用[16]。目前激光雷达主要有两种测距原理:三角测距原理与TOF测距原理[17],其中,TOF雷达可以测量的距离更远,并且可以在长距离范围内保持较高精度[18]。
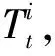
(1)
则无人机到第i个障碍点的距离di为:
(2)
式中:c表示电磁波传播速度。
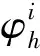
(3)
1.2.2 无人机运动模型
给定无人机某一时刻的运动速度大小改变量与航向角改变量,通过无人机运动方程来计算无人机的下一时刻位置,实现无人机的运动控制。
设定无人机的控制量更新周期为Ts,通过式(4)便可计算出其下一航迹点位置。
(4)
式中:v(t)为t时刻无人机运动速度大小;α(t)为t时刻无人机航向角。其更新公式为:
(5)
式中:Δv及Δα分别为t时刻的速度改变量及航向角改变量,单位分别为m/s及rad/s。
1.2.3 环境模型
文献[19]将障碍物划分为平面类、棱角类、弧形类3类,成功实现了障碍物的形状识别。文献[20]将不规则障碍物进行分割或者补全为规则的四边形、圆形等凸多边形,再利用几何法计算无人机登陆点,最后选取最优路径实现避障。
本文将障碍物简化为3类,分别是四边形、三角形、圆形,其他复杂障碍物均可以由这3类组合而成。为模拟未知环境,无人机在飞行过程中只能获取探测半径以内的障碍物信息。
1.3 无人机避障流程
无人机的实时避障流程如图2所示。

图2 无人机避障流程
如图3所示,设无人机自身位置与目标点之间的距离为Df,无人机与目标点最大许可距离为Da。将Da作为判断无人机是否抵达目标点的依据,即当无人机与目标点的距离小于最大许可距离时,认为无人机已经到达目标点。探测器获取的附近障碍物的最小距离为Dmin,无人机探测半径为Rd。
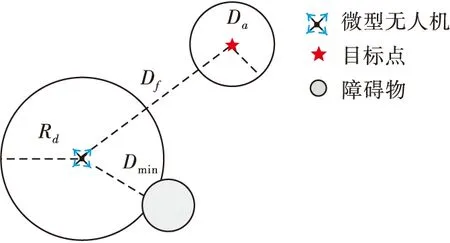
图3 避障流程参数说明
Step1无人机开始飞行并检测距离Df,如果Df>Da,即无人机与目标点的距离大于最大许可距离,转到Step2,否则转到Step5;
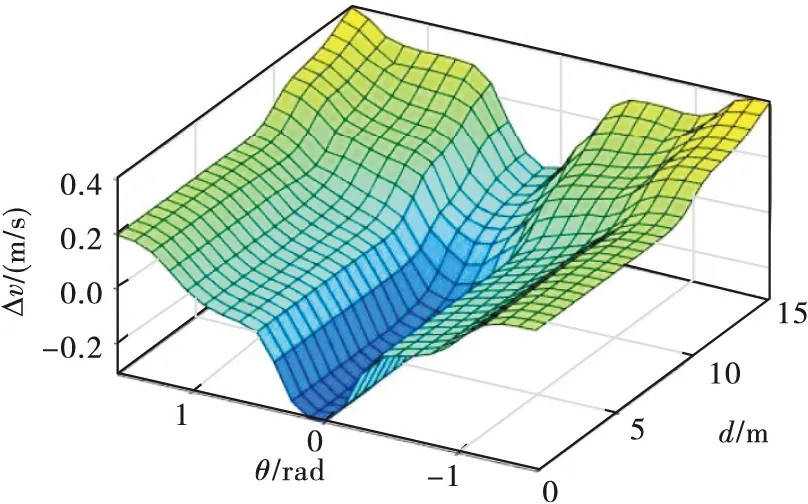
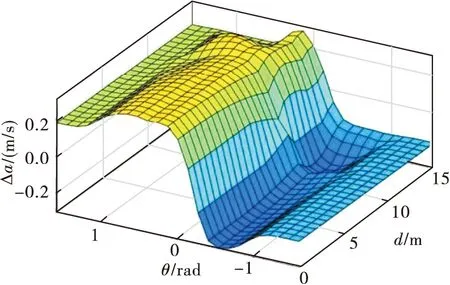
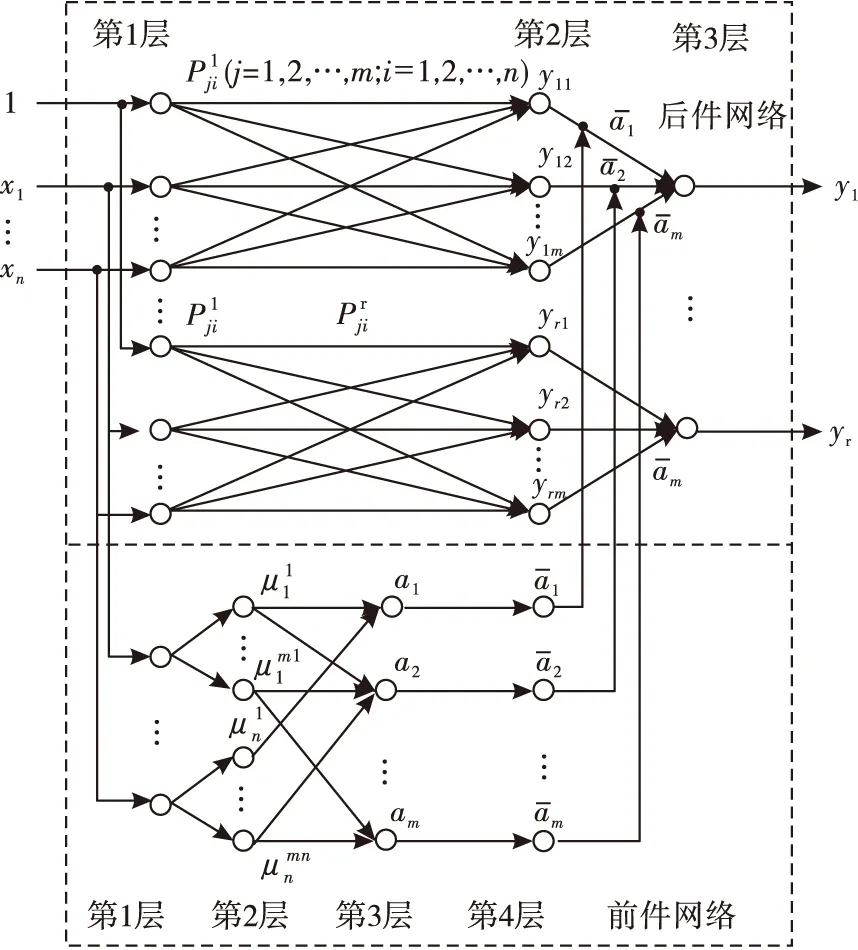
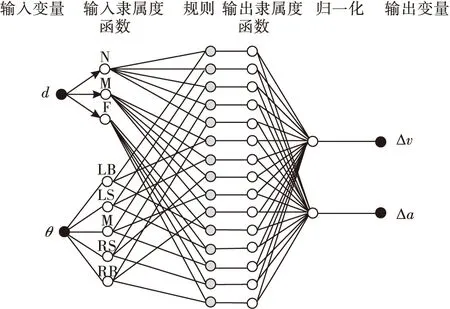
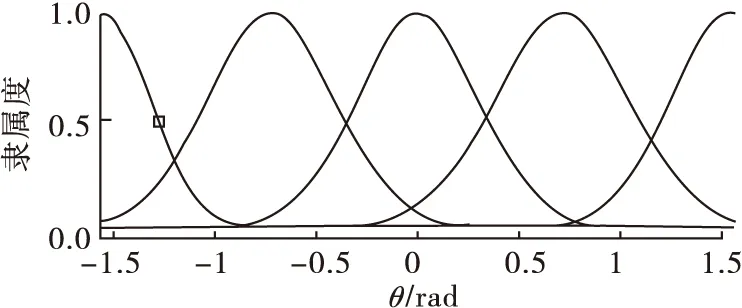
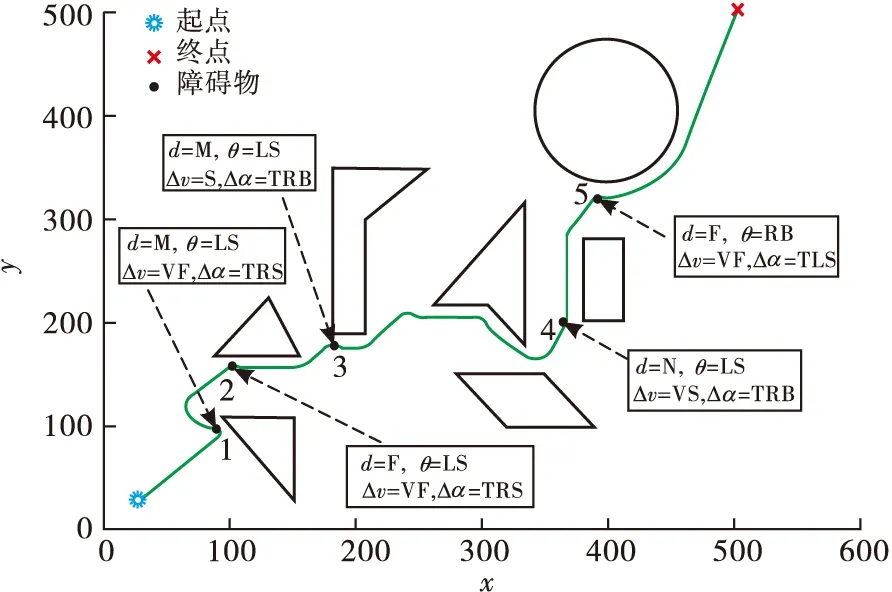
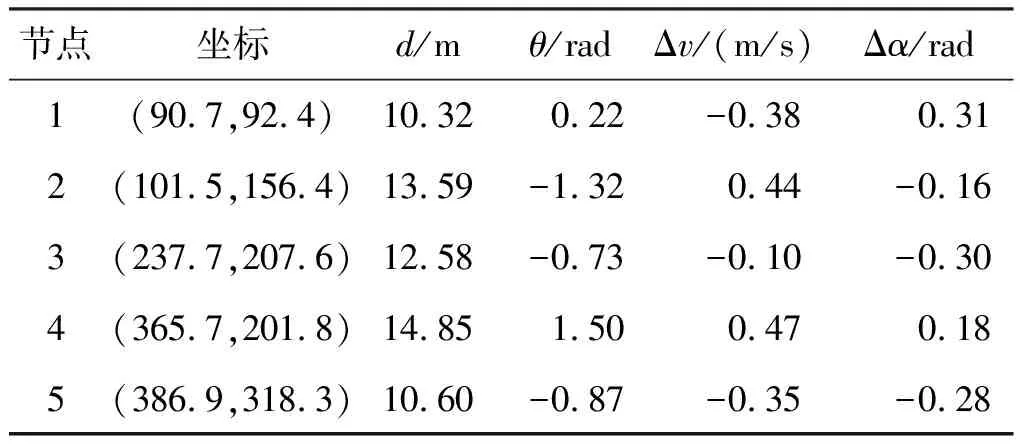
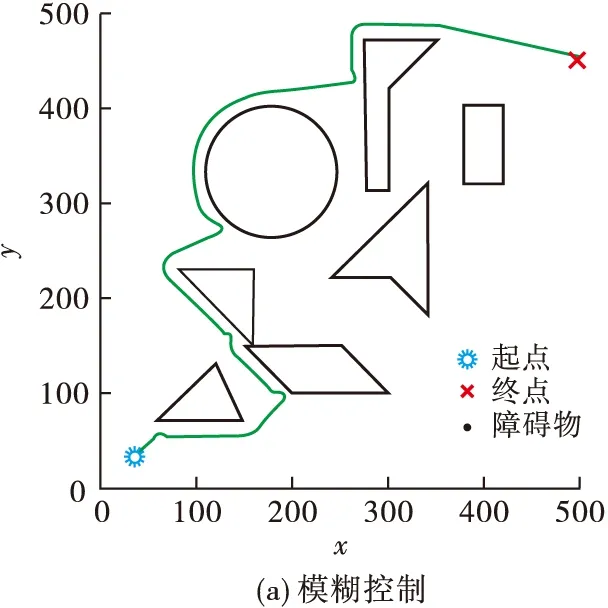
Step2无人机实时探测障碍物,如果探测到障碍物,即Dmin Step3无人机获取到障碍物距离与角度信息,在模糊神经网络控制器下进行避障,转到Step2; Step4无人机在目标点的引力作用下,以当前位置与目标点连线为航向角飞行,逐渐增大速度,转到Step1; Step5抵达目标点,结束飞行。 为获取模糊神经网络避障算法的训练数据,首先需要设计能够有效规避障碍物的Mamdani型模糊控制器,然后提取无人机在避障过程中的数据,最后用于模糊神经网络的训练。 2.1.1 输入变量定义 为了使障碍物信息得到充分利用,将模糊控制器的输入变量定义为无人机到探测范围内障碍点的最小距离d和无人机当前运动方向与无人机与障碍点连线形成的等效夹角θ,如图4所示。 图4 模糊控制器输入变量 O点表示无人机当前位置,E表示目标点,D1,D2,…,Dn表示在无人机探测范围内的障碍物边界离散点,n为探测范围内的障碍点个数,di为无人机到探测范围内第i个障碍点的距离,则模糊控制器第1个输入变量d为: d=min{d1,d2,…,dn} (6) 将式(1)、式(2)代入式(6)得到d的计算公式: (7) (8) θi为无人机当前运动方向与无人机与第i个障碍点连线的夹角,其计算公式为: (9) 将式(3)、式(9)代入到式(8)得到θ计算公式: (10) 2.1.2 输出变量定义 本文中无人机的运动状态由速度大小与航向角确定,输出变量设计为运动速度大小改变量Δv与航向角改变量Δα。 2.2.1 输入变量隶属度函数 对于输入变量d,其论域是由无人机最大探测范围所决定的。目前市面上的激光雷达,例如HOKUYO公司的UST-05LX,SLAMTEC公司的RPLIDAR等,能够很好地实现对15 m以内障碍物的探测,因此确定d的模糊论域为[0,15],单位为m,模糊分割数为3,模糊集合为{近,中,远}={N,M,F}。其中“近”表示无人机与障碍物距离较近,“中”、“远”含义同理。其隶属度函数采用高斯分布,如图5所示。 图5 输入变量d隶属度函数 对于输入变量θ,其论域是由无人机运动方向与无人机与障碍物相对位置关系共同确定,如图6所示。 图6 输入变量θ范围 只有θi为锐角时,才认为此时的障碍点Di对无人机有碰撞威胁,否则忽略不满足该条件的点。因此,θ模糊论域为[-π/2,π/2],单位为rad,模糊分割数为5,模糊集合为{左大,左下,中,右小,右大}={LB,LS,M,RS,RB},其中,“左大”表示障碍物主要集中分布在无人机运动方向的左侧,且与无人机运动方向的夹角较大。其他模糊语言的含义同理,其隶属度函数定义如图7。 图7 输入变量θ隶属度函数 2.2.2 输出变量隶属度函数 为实现无人机更精确的控制,将输出变量Δv、Δα的模糊分割数设计为5。同时为使无人机的运动轨迹更为平滑,需要考虑其运动学约束,本文限定了无人机的最大加速度与最大角速度。无人机的控制量更新周期Ts=0.25 s,速度改变量Δv论域范围为[-0.5,0.5],即无人机加速度大小最大为2 m/s2,模糊集合为{骤减,减速,匀速,加速,骤增}={VS,S,M,F,VF}。其隶属度函数采用高斯分布,如图8所示。 图8 输出变量Δv隶属度函数 无人机最大角速度确定为1.57 rad/s,根据控制量新周期Ts=0.25 s,因此航向角改变量Δα论域范围为[-0.393,0.393],模糊集合为{左大,左小,中等,右小,右大}={LB,LS,M,RS,RB}。其中“左大”表示航向角增加较大角度;即无人机向左转较大角度;“中等”表示无人机航向角不发生明显改变,其他模糊语言含义同理。其隶属度函数如图9所示。 图9 输出变量Δα隶属度函数 2.2.3 模糊控制器规则设计 模糊控制器的规则设计,需要在已有经验的前提下,给定输入、输出变量的对应关系,保证无人机能够实现躲避障碍物的功能。本文设计的两个输入变量d、θ的模糊分割数分别为3、5,因此共有15条规则,如表1所示。 表1 模糊控制器规则表 当输入变量d为“N”,θ为“LS”时,输出变量Δv为“VS”,Δα为“TRB”,即当无人机距离障碍物近,且当前航向角方向与无人机与障碍物连线夹角较小时,需要减速,减小航向角,使无人机低速右转,从而安全规避障碍物。 2.2.4 输出量控制曲面 图10反映了模糊控制器的输出变量Δv、Δα与输入变量的变化关系。 图10 速度与航向角控制曲面 由图10可知,随着d和|θ|的减小,输出变量Δv减小。说明无人机距离障碍物越近,航向角越靠近障碍物,则越需要低速飞行。且Δv、Δα的变化较为平滑,保证了无人机飞行过程中能够满足运动学约束。 模糊控制器采取固定的规则来实现无人机的避障要求,控制过程简单,实时性较好。但是其控制器的参数与规则确定后无法更改,适应性较差,当面对不同的环境时,规划路径效果不理想。此外,由于固定规则的限制,面对“凹多边形”障碍物时,容易进入“陷阱”,无法实现避障要求。 模糊控制适应性差,在障碍物分布差异较大的新环境中避障效果不稳定。而模糊神经网络在通过训练后,能够充分利用输入信息,提取障碍物的深度特征,提高避障算法对环境的适应性,使无人机在障碍物较为复杂的环境中也能够完成避障任务。 在模糊系统中,主要有Mamdani模型和Takagi-Sugeno模型。Takagi-Sugeno型模糊推理计算简单,有利于数学分析,且易于和PID控制方法以及优化、自适应方法相结合[21]。 图11为Takagi-Sugeno模型的模糊神经网络结构。该网络由前件网络和后件网络两部分组成[22]。前件网络由4层组成,其作用分别为传递输入,计算隶属度、计算适应度以及归一化。后件网络有yi个结构相同的并列子网络组成,每个子网络生成一个输出量。自网络的第1层为输入层,将输入传递给第2层。第2层用于计算每一条规则的后件,即: 图11 基于Takagi-Sugeno模型的模糊神经网络结构图 (11) 式中:j=1,2,…,m;i=1,2,…,r。 子网络的第3层是计算系统的输入,即: (12) yi是模糊神经网络的输出,由各规则后件加权和计算,加权系数为各模糊规则经归一化的使用度,即前件网络的输出用于后件网络第3层的连接权值。 本文利用MATLAB中的自适应神经模糊推理系统工具箱来完成模糊神经网络的设计与训练。首先无人机在模糊控制下进行避障,提取避障路径中的d、θ、Δv、Δα参数生成训练数据。然后将前文所设计模糊控制器中的输入变量及隶属度函数作为初始参数。由于d、θ模糊分割数分别为3、5,因此初始模糊神经网络同样有15条规则,每条规则下都对应一个输出变量的隶属度函数。MIMO的模糊规则可分解为多个MISO模糊规则,因此分别对Δv、Δα进行训练。图12为Δv、Δα的初始模糊神经网络结构。 图12 输出变量Δv、Δα训练网络 第1层为输入变量层,将输入变量值传递给网络;第2层为输入变量隶属函数层,其中定义了初始的隶属度函数;第3层为规则层,规则均采用and逻辑;第4层为输出变量隶属度函数,每个隶属度函数由输入变量通过线性运算得到;第5层为归一化层,第6层为输出变量。 之后将初始模糊神经网络、训练数据、测试数据导入至模糊推理系统编辑器,并设置训练算法、误差精度以及训练次数。 本文选择混合算法,训练误差为0.003,训练次数为40。训练完成的输入变量隶属度函数如图13所示。 图13 输入变量d、θ训练结果 与初始隶属度函数(图5~7)相比,该隶属度函数的中心值与宽度值有了较大改变。最后将训练完毕的模糊神经网络在新的仿真环境中进行测试,验证其避障效果。 仿真环境为600 m×600 m的正方形,以原点(0,0)建立直角坐标系,起始点坐标(30,30),目标点坐标(500,500),无人机最大速度vmax=4 m/s,最小速度vmin=1 m/s,控制量更新周期Ts=0.25 s,最大角速度ωmax=1.57 rad/s,最大加速度amax=2 m/s2,最大探测半径Rd=15 m。 图14为模糊控制器在仿真环境下的避障效果,从图中可以看出,在多次调整隶属度函数和模糊规则后,控制器能够实现较好的避障效果,且运动轨迹平滑,安全性较高。图中标注出了5个关键避障节点,其飞行仿真数据见表2。根据表中的数据与输入、输出变量隶属度,可以确定每个节点无人机所采取的模糊规则,证实了模糊控制器实现避障的可行性。 图14 模糊控制器避障结果 表2 关键节点飞行数据 但是模糊控制算法采用固定规则来实现避障,试凑法确定的模糊控制器参数无法实时变化。当环境发生改变时,适应性较差。此外,基于经验设计的规则只考虑了简单的障碍物分布情况,当环境中存在复杂“凹多边形”区域,无人机便会进入“陷阱”,无法实现避障要求。 图15为两种算法在新的障碍物环境中的避障效果对比。与图14相比,环境中的障碍物位置发生了变化。对比两图可知,两种算法都能实现避障,但在面对同一障碍物时,规划的避障路径却不同。模糊控制器按照固定的规则,当θ为M时,只能采取向左飞行规避障碍物的策略。而模糊神经网络控制器则能根据训练数据,提取障碍物特征,根据不同的障碍物采取更优的避障策略。 图15 模糊控制、模糊神经网络仿真结果对比 图16为在该环境中采用两种避障方法的无人机飞行状态对比图。模糊控制规划路径长度为1 046.4 m,模糊神经网络规划路径长度为938.7 m。由图可知,在118 s时无人机采取了不同的避障动作,路径抵达目标点的时间分别为244 s和271.75 s。模糊神经网络缩短了避障路径,能够更快到达目标点。 图16 飞行状态对比 图17为其中另一新环境中的避障效果对比,该环境中存在局部的“凹多边形”障碍物区域。 图17 随机环境中模糊控制、模糊神经网络仿真结果对比 模糊神经网络经过大量避障数据的训练,能够提取障碍物分布的深度信息,其输出是输入的线性组合,并不依赖固定的规则。当无人机进入到“凹多边形”区域内时,能够根据障碍物特征,做出“后退”的飞行动作,从“陷阱”中脱离。 最后,通过蒙特卡罗仿真实验比较模糊控制与模糊神经网络算法的避障效果,验证模糊神经网络具有更强的适应性。首先以文中的7个障碍物模型为基础,随机更改它们的位置,生成了500张障碍物地图。然后无人机在两种控制算法下分别进行避障仿真,并统计无人机的避障次数、路径长度与飞行时间。实验结果如表3所示。 表3 避障仿真实验结果 在500次的仿真实验中,模糊神经网络算法的避障成功率更高,平均路径更短,飞行时间更少,说明了该算法有更强的适应性。 但是由于无人机在未知环境中规划的是局部路径,且模糊神经网络算法没有考虑障碍物信息处理、环境信息融合等问题,因此依然存在部分“凹多边形”区域影响无人机的避障效果。另外,由于全局环境信息未知,模糊神经网络只能得到可行解,并非最优解。针对未知环境中如何得到最优路径问题,还需更深入的研究与探讨。 本文采用等效夹角优化了模糊控制器的输入变量,将模糊控制应用于无人机未知环境中的避障,生成了避障路径。然后提取路径数据,设计并训练模糊神经网络,并进行了蒙特卡罗仿真实验,比较了两种算法的避障效果。结果表明模糊神经网络算法的适应性更强,能够优化局部避障路径,规避分布较为复杂的障碍物,在未知环境中的避障成功率更高。2 基于模糊控制的避障算法
2.1 模糊控制器输入输出变量定义
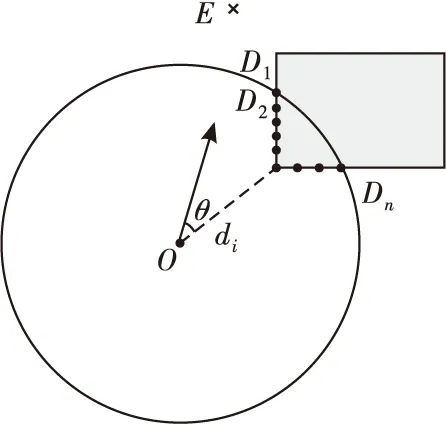
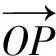
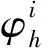
2.2 模糊控制器隶属度函数定义
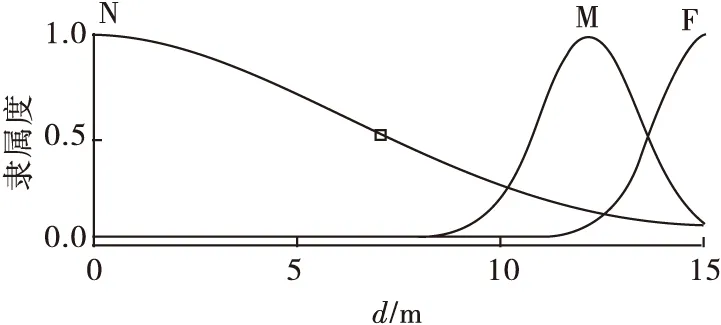
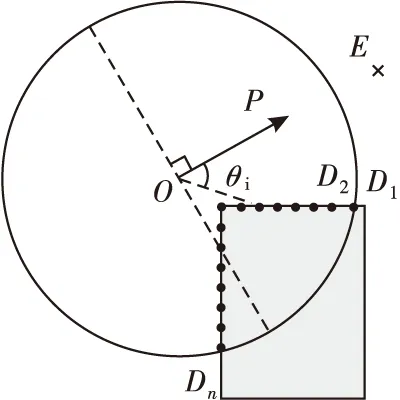

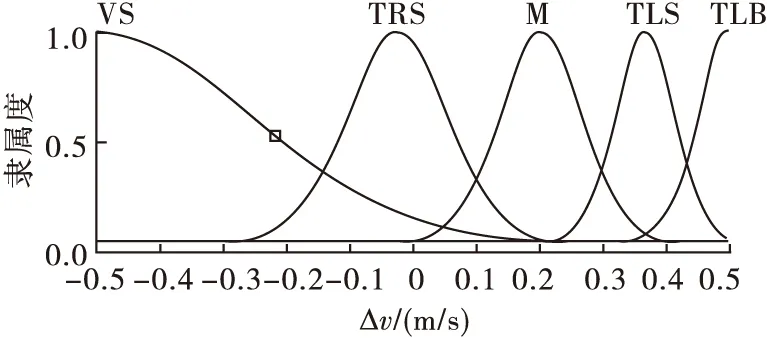
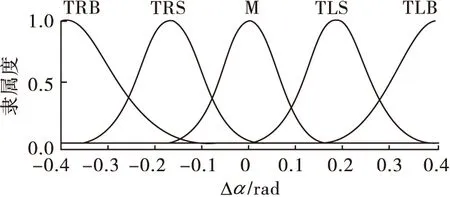
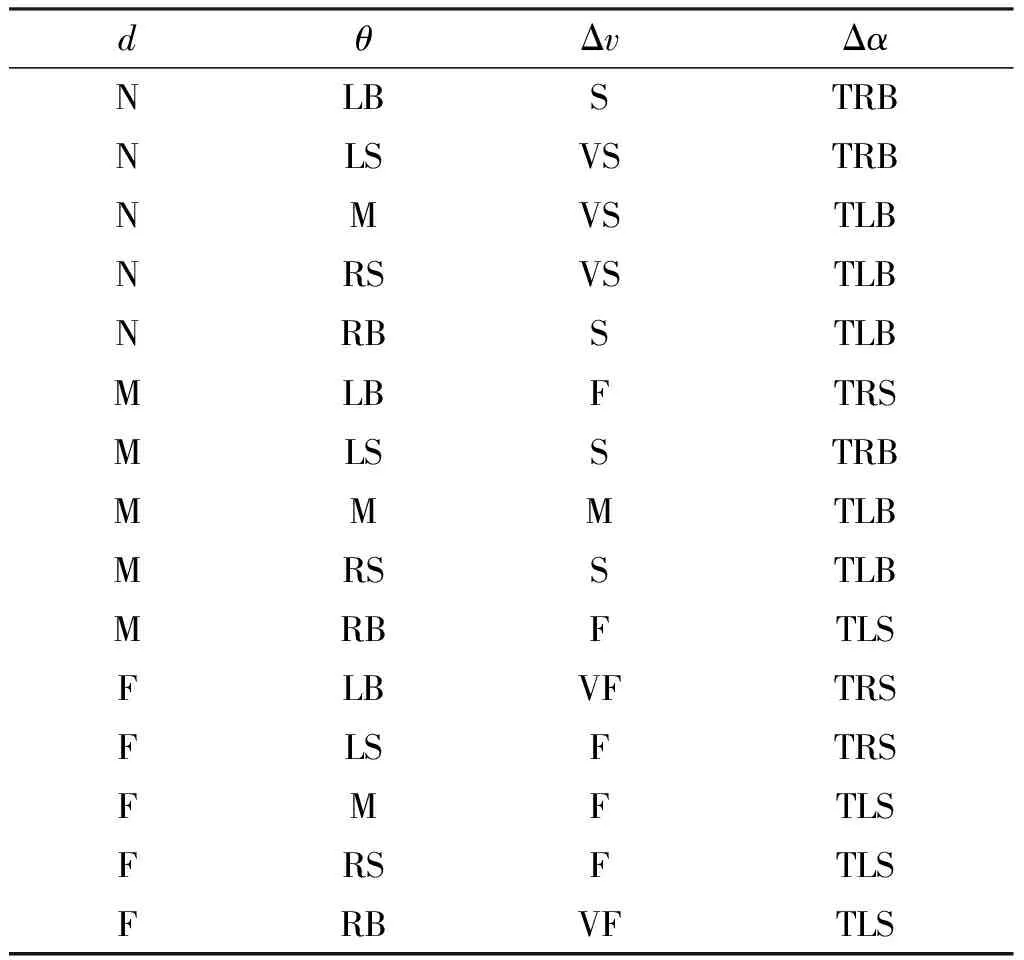
3 模糊神经网络避障算法
3.1 模糊神经网络
3.2 模糊神经网络的结构和参数训练流程

4 仿真结果
4.1 仿真条件
4.2 模糊控制避障仿真结果
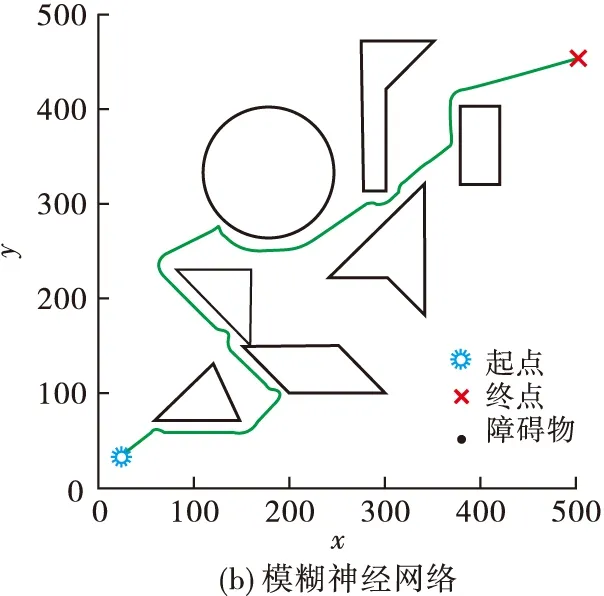
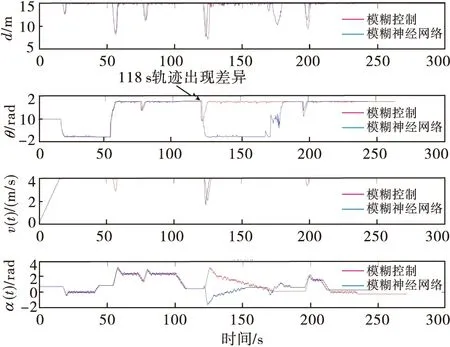
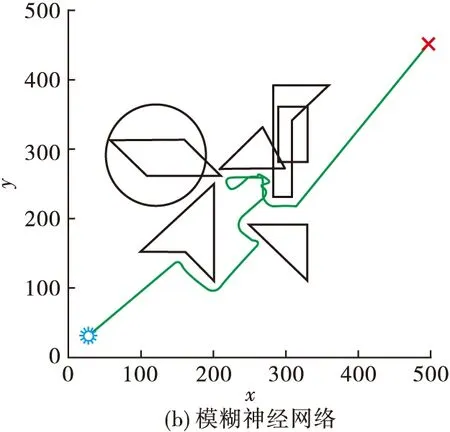
4.3 模糊控制与模糊神经网络避障仿真对比


5 结语
