防空反导装备指控舱显控台界面布局优化设计与评价
2021-12-22王大颜张港生
王大颜, 瞿 珏,2, 王 崴, 张港生,朱 帅
(1.空军工程大学防空反导学院, 西安, 710051; 2.西北工业大学航空学院, 西安, 710072)
防空反导装备指控舱显控台显示界面的直感交互设计是指针对目前指控台上显示界面所存在的问题应用直感交互相关理论进行界面元素以及界面布局的设计。在当前防空反导装备的显示界面上,存在着状态参数显示重复过多,元素颜色不直观以及部分参数的位置设计不合理等问题,导致操作人员无法准确的获得战场上的关键信息,增加了认知负荷,降低了操作绩效。
传统的界面设计已经无法满足操作人员的需求,而界面的直感交互设计可以充分地考虑操作人员的认知特性[1-5],有效降低操作人员的认知负荷[6],提高操作绩效。针对界面的多指标综合评价,目前较为适用的评价方法有灰色综合评价法和模糊综合评价法[7-9]。模糊综合评价法相比较于灰色综合评价法更适合用于多种方案的优选[10-15]。
本文主要针对防空反导装备显控台显示界面显示区域不合理的问题进行界面设计和评价。依据作战任务流程,将界面元素分区划分为5个区域,并建立直感交互界面布局模型对防空反导装备显控台界面进行直觉化设计。最终应用多属性模糊综合评价法进行优化界面的评价,验证了界面优化设计的有效性。
1 建立界面布局模型
本文依据任务流程中指挥控制显控台人机界面的功能和特征,将界面元素分为信息显示区、火力参数区、系统状态区。目前态势信息显示区的表格显示区的颜色搭配和布局位置不合理,图符与目标的关联度差,即隐喻度较低。火力参数区中状态参数显示重复过多、功能、状态均使用文字-颜色特征捆绑进行区分,火力参数区位置不合理,使得操作人员对状态参数的直感交互程度低。系统状态区布局位置不合理,占据了界面较大的面积,指挥控制席系统状态栏不同装备和系统之间颜色及区域划分不明显,不符合格式塔原则[16-17]。总之,3个不同的区域都存在着布局位置不合理的共性问题,因此本文从界面的布局方面出发,将隐喻度、直感交互、格式塔原则引入界面设计中,从而解决界面设计不合理的问题。
指挥控制显控台完成作战任务需要多种显示和交互控件,这些控件依据功能布置在不同的区域中,设待布区域的总数为M个,则直感交互界面布局设计模型可以描述为将M个待布区域合理地分配到交互界面中,并满足约束条件、设计原则以及优化目标。图1所示为布局设计模型示意图[18]。

图1 直感交互界面布局设计模型示意图
以界面左下角为布局空间原点o,建立二维坐标系o-xy。设待布显示和交互区域共有M个,则第i个待布区域c可用其中心坐标ci=(xi,yi,βi)表示,其中xi,yi表示第i个待布区域在坐标系中的坐标[18]。
防空反导装备布局设计可以看作典型的组合优化问题,即寻求最优待布区域坐标组合解,在满足约束条件的情况下实现多目标最优。本文以待布区域序列C=(c1,c2,…,cM)为设计变量,区域的位置序号与待布区域一一对应,则布局设计问题可用式(1)的数学模型表达[18]:
C={c1,c2,…,cm},
(1)
式中:ck表示位置k处对应的待布区域的序号。
2 模糊层次分析法
2.1 量化分析方法的选择
人机交互过程中具有很多不确定的因素,采用传统的分析方法很难将其中的不确定性展示出来。直觉化的人机界面比传统的界面更强调一种界面对能够体现操作人员直觉的生理参数的理解。传统的层次分析法在检验判断矩阵是否一致时非常困难,并且检验判断矩阵是否具有一致性缺乏科学的依据[18]。模糊层次分析法不仅可以将人机交互过程中的不确定性表示出来,可以将直觉交互界面的直觉性表达出来。因此,本文采取模糊层次分析法(fuzzy analytic hierarchy process,FAHP)进行布局原则的量化。
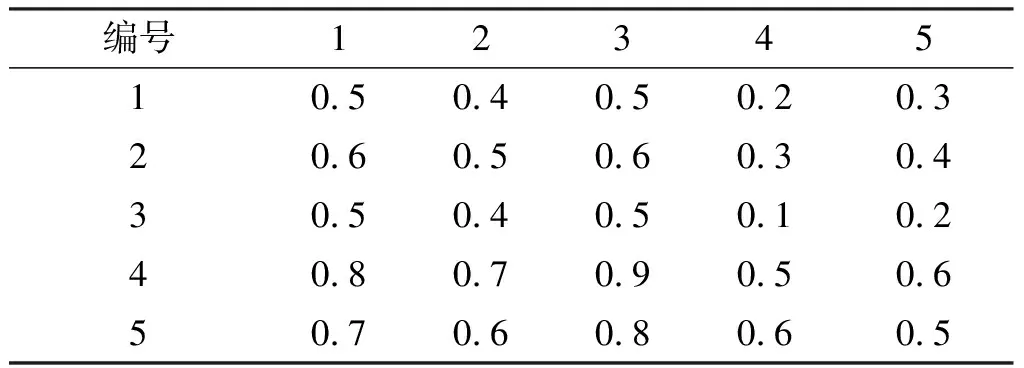
在进行直感交互界面设计时,首先根据表1的标度方法对相关设计原则进行两两比较,从而构建出判断矩阵A=(aij)n×n。如果A中的元素满足式(2),则将此判断矩阵称为模糊互补的判断矩阵:

表1 判断矩阵标度
aii=0.5,i=1,2,…,m
aij+aji=1,i,j=1,2,…,m
(2)
建立模糊判断矩阵之后,还需要进行权重的计算以及一致性的检验。模糊判断矩阵的权重计算为:
(3)
式中:aij为判断矩阵第i行第j列的元素,m为待布区域个数。
由于布局问题涉及的因素较多,而且对待布区域的认知较为模糊,判断矩阵的一致性较低,因此本文采用陈友华等[19]提出的一致性检验方法:
1)相容性指标:设矩阵A=(aij)n×n和B=(bij)n×n均为模糊判断矩阵,则矩阵A和B的相容性指标可表示为:
(4)
2)特征矩阵:设W=(W1,W2,…,Wn)T为A的权重向量,其中:
(5)
令Wij=WiWj+Wj,(i,j=1,2,…,n),则A的特征矩阵为:
W*=(Wij)n×n(4)
(6)
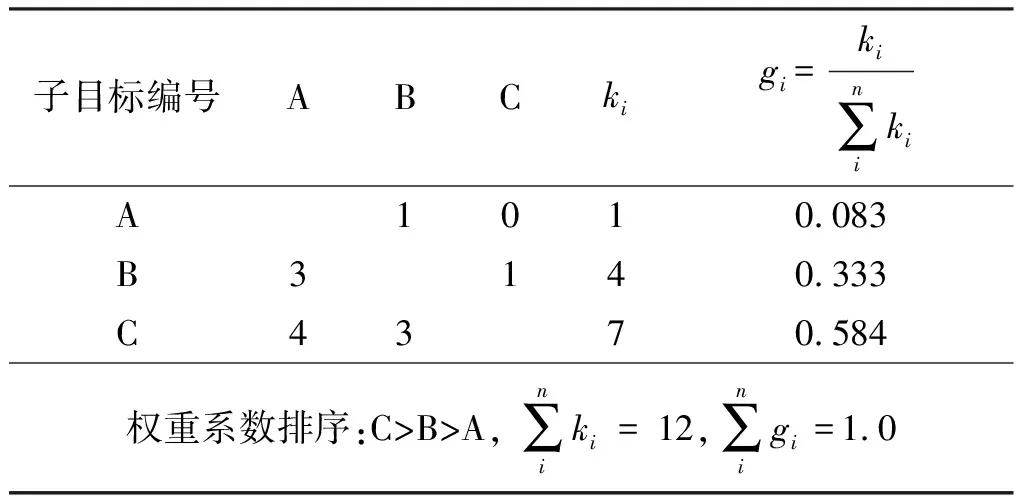
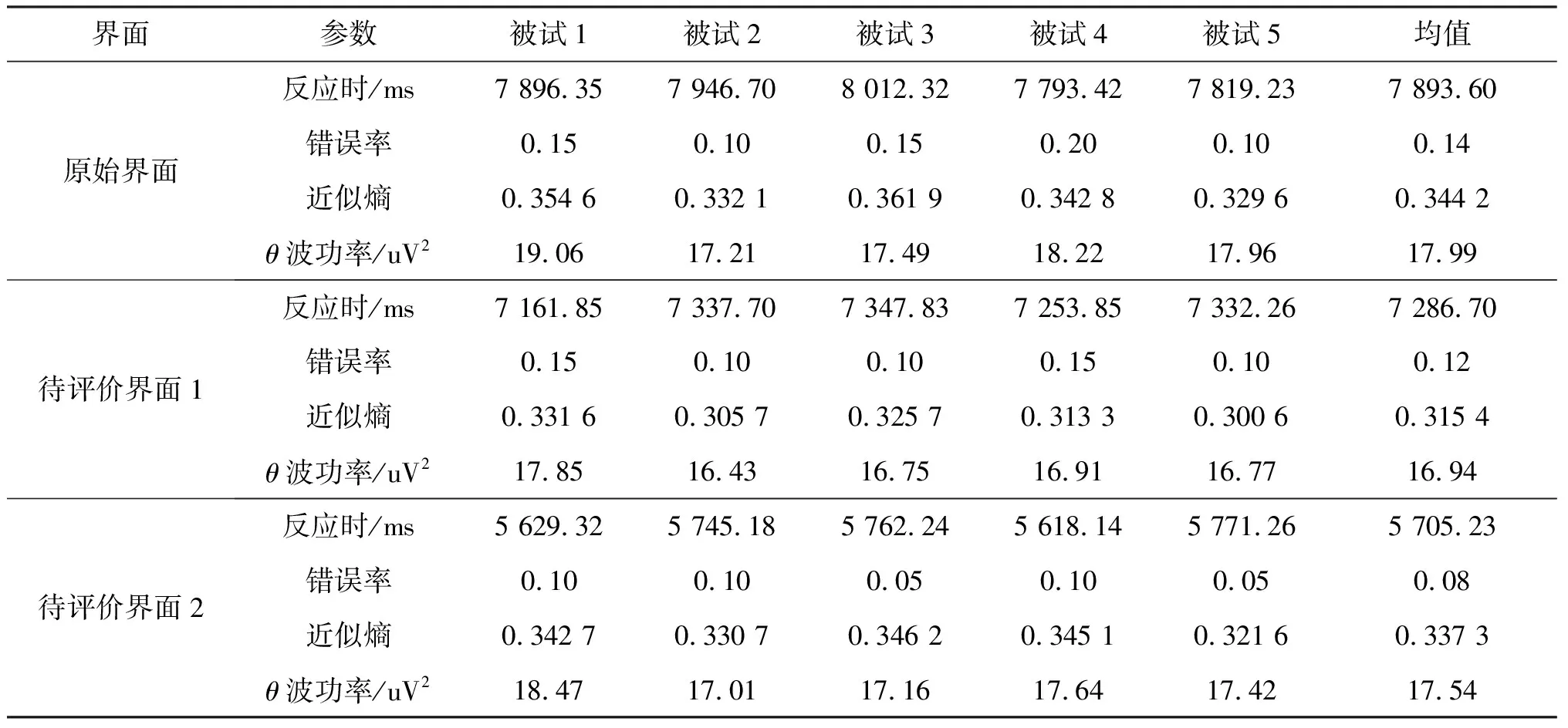
如果相容性指标I(A,B) 2.2.1 隐喻度子目标函数 隐喻是直感交互界面常用的设计方法,每个区域的隐喻度是直感交互界面布局的重要考量因素。我们邀请武器系统人机交互设计专家、学院教员以及参加接改装训练的战勤人员对每个区域的隐喻度进行评判,评判标准如表2所示。 表2 隐喻度矩阵标度 构建隐喻度模糊判断矩阵为: (7) 式中:r表示参与评价的人数;Mij表示第i个待布区域由第j个评价人员给出的隐喻度数值。 参与评价的人员的资历与权威不同,因此我们建立式(8)所示专家权重矩阵: ωZ=[ωZ1,ωZ2,…,ωZr]T (8) Zi=MijωZ (9) 根据式(3)计算隐喻度模糊判断矩阵的隐喻度权值,其中待布区域的重要度权值用Mai表示。根据式(4~6)进行一致性检验。 点P表示界面最佳视点,通常认为界面中心为最佳视点。用欧氏距离dip表示区域中心点到最佳视点P的距离,计算方法为: (10) 则各待布区域的隐喻度子目标函数为: (11) 式中:X=(x1,x2,…,xn)是待布区域在界面空间中x轴方向的坐标;Y=(y1,y2,…,yn)表示在y轴方向的坐标,待布控件i的x轴坐标与y轴坐标一一对应[18]。D为常数,其具体值与界面空间的大小、待布区域的形状有关,也可由专家确定。 2.2.2 重要度子目标函数 待布区域的重要度取决于区域中控件的功能以及战勤人员的主观认知,首先构建重要度模糊判断矩阵: (12) 式中:r表示参与评价的人数;Iij表示第i个待布区域由第j个评价人员给出的重要度数值。 则待布区域i的加权重要度评分为: Zi=IijωZ (13) 根据式(3)计算重要度模糊判断矩阵的重要度权值,其中待布区域i的重要度权值用Imi表示。根据式(4~6)进行一致性检验。 则各待布区域的重要度子目标函数为: (14) 2.2.3 使用频率子目标函数 操作人员执行防空反导人机交互任务时,点击某一区域的次数可以用来表征界面上某区域的重要程度,故某一区域的使用频率可以作为评判界面优劣的一个依据。通过专家给出的使用频率的矩阵可以表示为: (15) 式中:fij表示第i个待布区域在任务j中的使用频率评分。 在执行操作任务时,每个任务的执行频率决定每个任务的权重,并且相关的专家会结合以往的作战使用的数据和操作经验,给出概率矩阵的参考: ωE=[ωE1,ωE2,…,ωEg]T (16) 则待布控区域i的加权使用频率评分为: Ei=fijωE (17) 根据表1的标度法得出使用频率的模糊判断矩阵之后,根据式(3)计算使用频率模糊判断矩阵的重要度权值,其中待布区域i的使用频率权值用Fri表示。根据式(4~6)进行一致性检验。则各待布区域使用频率子函数为: (18) 2.2.4 子目标函数的权重 常见的确定权重的方法包括:专家打分法、聚类求均值法、因子排序法、层次分析法以及判别分析法等。本文采用对各个子目标函数的权重进行计算,见表3。 表3 各个子目标判别分析法计算示例 在对各个目标函数进行两两比较判断分析时,重要程度相同的分别2分;两者相比,较为重要的3分,另一个1分;两者相比,更重要的4分,另一个0分。子目标函数的权重系数为: (19) 式中:gi表示第i个子目标函数的权重系数;ki表示总分;n表示子目标函数的个数。 2.2.5 布局总目标函数 将各个子目标函数与子目标函数的权重系数结合起来,最终可以得到直感交互界面布局设计问题总目标函数: (20) 式中:fi(X,Y)为各子目标函数。 为了验证本文所提出的直感交互界面设计模型的有效性,我们以指挥控制显控台人机界面为例进行防空反导装备界面直觉化设计。该界面中包含的待布区域都可以被简化成长方形,通过测量可以得到各个区域的大小,如表4所示。布局空间的尺寸为515 mm×287 mm。原显示界面的布局见图2。 表4 待布控件尺寸 图2 原显示界面布局 2.3.1 布局设计模型子目标函数相关值 利用模糊层次分析法计算5个待布控件的隐喻度、重要度、使用频率子目标函数的相关权值。 1)隐喻度子目标函数。根据式(9)计算出各个待布区域的隐喻度加权评分,根据表1的标度方法构建表5所示的隐喻度模糊判断矩阵。 表5 隐喻度模糊判断矩阵 根据式(3~6)进行权重的计算以及一致性的检验后得到各待布区域的隐喻度权值,见表6。 表6 各待布区域的隐喻度权值 2)重要度子目标函数。根据式(13)计算出各个待布区域重要度加权之后的评分,之后根据所得结果进行排序并且计算各个区域评分之间的差值,最后依据评分和评分差值大小对照表1中给出的比较规则,构建出表7的重要度模糊判断矩阵。 表7 重要程度模糊判断矩阵 进行权重的计算以及一致性的检验后得到各待布控件的重要度权值,如表8所示。 表8 各待布控件的重要度权值 3)使用频率子目标函数。根据式(17)以及表1的标度法得出使用频率的模糊判断矩阵,如表9所示。 表9 使用频率模糊判断矩阵 进行权重的计算以及一致性的检验后得到各待布控件的使用频率权值,如表10所示。 表10 各待布控件的使用频率权值 最后利用判别分析法计算3个布局原则的权重,并将其带入适应度函数中(见表11)。 表11 各个子目标判别分析法计算示例 2.3.2 基于MATLAB的遗传算法求解 界面的直感交互设计需要更多考虑人机交互过程中的直觉性,具有不确定性和随意性,而遗传算法针对带有猜测性质的问题优化具有较大的优势,因此本文选用遗传算法进行布局优化问题的求解。 实验中,得到如图3所示的目标函数最优值曲线图,根据图3绘制如图4所示优化后界面布局几何简图,之后将实验所得结果应用到实际界面布局设计当中,如图5所示。 图3 目标函数最优值曲线图 图4 直感交互界面各个区域布局图 图5 优化后界面布局 本文对原始界面,基于灰色关联度的优化界面以及基于隐喻度子函数、重要度子函数和使用频率子函数的遗传算法的优化界面进行评价,界面分布如图6。原始界面图6(a)作为参考,图6(b)定义为待评价方案1,本文优化界面图5定义为待评价方案2。 图6 基于不同优化方法的界面布局 1)建立指标矩阵F对于由m个评价方案n个因素指标组成的因素指标矩阵F有: (21) (22) (23) 从而得出各对象的加权距离,其中将di中的最小者即di=min(d1,d2,…,dm)确定为最优方案。 近似熵和θ波功率计算公式分别为[20]: (24) (25) 依据式(24)和(25)计算得到该时间段的近似熵平均值和θ波功率平均值。脑电信号处理前后见图7~8。处理后的实验数据见表12。可以看出,优化方案不仅提高了被试的操作绩效,而且降低了被试的认知负荷。 图7 原始脑电信号 图8 预处理后的脑电信号 表12 实验任务数据 根据前文所述,由各评价对象构成的集合为: A={原始界面,待评价界面1,待评价界面2} 评价指标集合为: X={反应时间,反应错误率,近似熵,θ波功率} 对各评价指标进行标准化处理,得到3个评价对象在4个评价指标下的矩阵F为: (26) 利用德菲尔法[15]确定反应时间、反应错误率、近似熵以及θ波功率等评价指标的权重系数为: W=(0.367,0.349,0.142,0.142) (27) (28) 于是,可分别得到各评价对象指标值与最优值之间的广义加权距离: d1=1 (29) d2=0.585 (30) d3=0.387 (31) d=min(d1,d2,d3)=d3 (32) 从数据处理结果可以看出,优化后的界面设计提高了被试的反应速度和反应正确率,并降低了脑力负荷,待评价方案1和2更加合理。 本文提出了一种基于重要度子函数、隐喻度子函数和使用频率子函数的界面布局优化模型,该模型考虑到操作人员的操作习惯、认知和心理特性,并利用遗传算法进行求解;同时应用基于多属性模糊综合评价的界面评价方法,将传统的人机界面评价指标反应时间、反应错误率和操作人员的脑电指标近似熵、θ波功率相结合,完成了防空反导装备指挥控制台显示界面评价案例分析。利用本文的评价方法对原始界面、本文优化界面以及基于灰色关联度优化的界面进行评估结果证明本文优化模型优化的界面更加合理。 后续的工作将进行界面上其它显示元素的研究,比如显示图标的颜色、大小、目标的移动速度以及目标的动态显示等,进一步完善优化方案的界面评价指标体系,将操作人员的眼动数据和脑电数据结合起来,用于优化方案的评价,提高结论的可信度。2.2 构建子目标函数

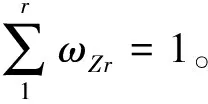
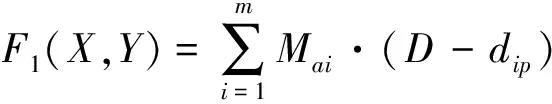

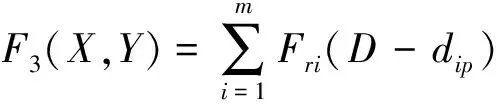
2.3 直感交互界面布局设计模型Matlab实现







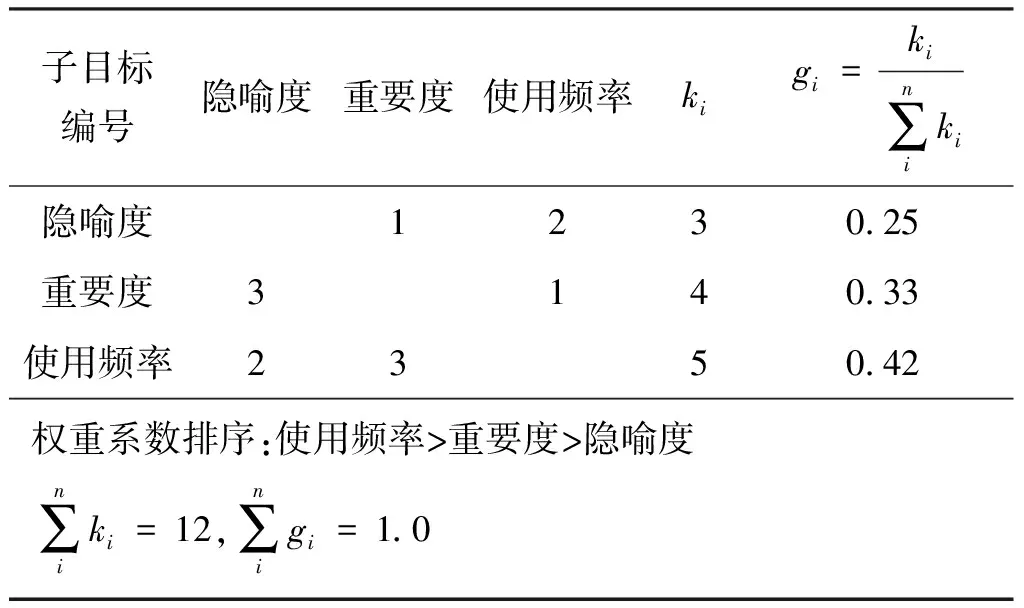


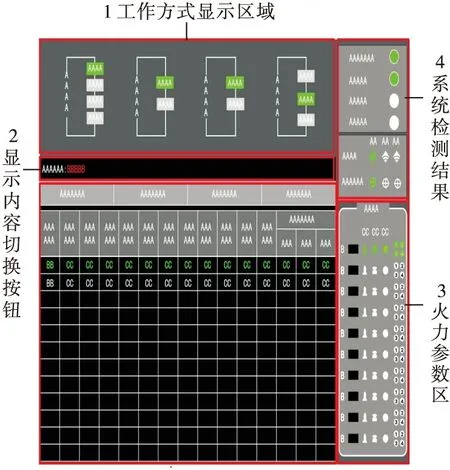
3 基于多属性模糊综合评价法的界面评价


3.1 建立模型


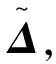
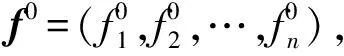
3.2 数据分析与处理




4 结语
