基于惩罚逻辑回归的乳腺癌预测

胡雪梅，谢 英，蒋慧凤

（1.重庆工商大学数学与统计学院，重庆 400067；2.重庆工商大学经济社会应用统计重庆市重点实验室，重庆 400067；3.重庆工商大学长江上游经济研究中心，重庆 400067）

引 言

乳腺癌目前是全球排列第一的肿瘤疾病，居女性恶性肿瘤发病率之首。2012年，170万名女性被诊断出患有乳腺癌，约52.2万名患者死亡。根据世界卫生组织国际癌症研究机构2018年发布的报告表示，乳腺癌病患数在各种癌症种类中排名第5，有将近210万女性乳腺癌新发病例，大约62.7万人死亡，而且随着人们饮食习惯和生活方式等方面的改变，乳腺癌恶性肿瘤的发病率会呈递增趋势。与美国相比，中国的乳腺癌患者生存率偏低，这与中国人口基数过多、有经验的影像科医生缺乏、难以实施大范围早期筛查有关。癌症早期被发现时容易治愈，因此准确筛查癌症早期患者至关重要。

目前乳腺癌的诊断方法主要有X射线诊断［1］、CT扫描、临床触诊、超声波显像检查、核磁共振成像术、近红外线扫描、钼靶和细针穿刺细胞病理学检查等。乳房X光是一种测试方法，但也存在缺点，经常会导致假阳性结果，导致不必要的活检和手术，在乳房X光片上看到具有可疑的异常细胞时，需要通过手术去除异常细胞，然而大部分肿瘤在手术中被发现是良性的，这意味着每年都有数千名妇女无端承受手术痛苦、昂贵费用和术后疤痕等。传统的诊断方法可能会由于低劣的图像质量以及临床医生的视觉疲劳或疏忽等导致漏诊或误诊。现在可以借助计算机技术辅助诊断帮助医生和乳腺癌患者。

深度学习是机器学习中一个非常接近人工智能（Artificial intelligence，AI）的领域，具有强大的能力和灵活性，能将大千世界表示为嵌套的层次概念体系：（1）无监督学习用于每一层网络的Pre⁃train；（2）每次用无监督学习只训练一层，将其训练结果作为其高一层的输入；（3）用监督学习去调整所有层。通过组合低层特征形成更加抽象的高层表示属性类别或特征，发现数据的分布式特征表示，建立模拟人脑进行分析学习的神经网络，模仿人脑机制解释图像、声音和文本等数据。深度学习目前在计算机视觉、图像处理、语音识别和自然语言处理等领域应用很成功，在病理成像等医学图像模式的分类和检测方面表现不俗。机器学习涉及大量统计理论，与统计推断联系密切，故也称为统计学习。机器学习通过设计自动“学习”算法，从数据中自动分析获得规律并对未知数据进行预测，已成功应用于很多领域。例如，从检测信用卡交易欺诈的数据挖掘程序，到获取户阅读兴趣的信息过滤系统，再到能在高速公路上自动行驶的汽车等。机器学习［2⁃6］还可以有效辅助医生诊断，帮助医生筛查乳腺癌等病症。例如，Huang等［7］开发了计算机辅助诊断（CAD）系统，用支持向量机对118个乳腺肿瘤作良性和恶性分类，分类效果很好；Montazeri等［8］利用朴素贝叶斯、树随机森林、支持向量机和多层感知器等机器学习方法结合10折交叉验证预测不同乳腺癌的生存率，并用准确度、灵敏度和ROC曲线下的面积（Area under curve，AUC）等评价几种方法，得出树随机森林效果更好（96%、96%、93%）；Xia等［9］利用卷积神经网络对不同类型的乳腺癌细胞Mueller偏振成像图进行分类，准确率达到了88.3%等。

支持向量机只能预测类指标，不能提供类概率估计。神经网络因为噪音累积、非平稳特征和复杂维数在学习方式上有限制等原因导致预测精度不稳定，时高时低。逻辑回归不仅能预测类指标，还能得到类概率估计，并且能获得较高的预测精度。例如，胡雪梅等［10］比较了逻辑回归、支持向量机、人工神经网络、ELMAN神经网络和基于五类统计指标的一阶自回归逻辑回归模型的预测表现，发现逻辑回归模型预测表现最好。而惩罚逻辑回归是对逻辑回归引入惩罚函数，选取重要变量作分类预测，可以进一步提高模型的拟合能力与预测精度。因此，本文采用惩罚逻辑回归来预测乳腺癌肿瘤是良性还是恶性问题。

近年来，人们提出了不同惩罚逻辑回归作分类与预测研究。例如，Park等［11］采用L2惩罚逻辑回归探测基因的交互影响，可以识别交互结构和重要因子，并且得到合理的预测精度；Meier等［12］提出了组LASSO惩罚逻辑回归及其衍生模型：组LASSO⁃Ridge混合惩罚逻辑回归和组LASSO⁃MLE混合惩罚逻辑回归，发展了坐标下降算法，通过DNA剪接位点预测研究发现组LASSO惩罚逻辑回归是最佳预测模型；Friedman等［13］发展了具有LASSO惩罚、L2惩罚、弹性网惩罚的广义线性模型（包含线性模型、逻辑回归和多项式回归）及其坐标下降算法，设计了glmnet程序包；Ayers等［14］在基因关联研究中选择单基因多态性（Single nucleotide polymorphisms，SNPs）作为预测变量，利用5类惩罚逻辑回归：弹性网惩罚、L2惩罚、LASSO惩罚、MCP惩罚和正态指数伽玛分布（Normal exponential Gamma，NEG）惩罚作为两类分类器预测灵敏度和特异度；Breheny等［15］对具有分组预测变量的非凸惩罚线性回归和逻辑回归发展了组坐标下降算法，重点介绍了组LASSO、组SCAD和组MCP惩罚逻辑回归及实际数据预测分析；Li等［16］建立了基于弹性网正则化的相关性逻辑回归多标签图像分类模型，对标签间的成对相关性建模以提高多标签分类（Multi⁃label classification，MLC）的有效性，充分利用特征选取和标签相关的稀疏性，采用弹性网正则化进一步提高MLC的性能，并用4个多标签图像数据集证实模型的有效性；Sari等［17］分别采用LASSO惩罚逻辑回归和支持向量机作信用评分分析，两种方法的分类精度基本相同（79.2%和79.94%），但SVM的分类效果更稳定（灵敏度：79.80%和72.62%）；Münch等［18］提出了分组弹性网逻辑回归，能够改进特征选取和分类表现，用3组癌症基因模拟证实分类性能和特征选择得到了改进；Garcia⁃Carretero等［19］发展了逐步逻辑回归、LASSO惩罚逻辑回归和弹性网惩罚逻辑回归预测高血压肥胖人群维生素D缺乏症，并采用灵敏度、特异度、误分类率和AUC评价3种方法的预测表现，结果表明，LASSO惩罚逻辑回归和弹性网惩罚逻辑回归得到的AUC显著高于逐步逻辑回归，能更准确地预测维生素D缺乏症等。

诊断乳腺肿瘤是良性还是恶性本质上是一个二分类问题。本文先从威斯康星州大学的乳腺癌数据选取10个指标作为预测变量，将诊断结果（良性：Y=0和恶性：Y=1）作为响应变量，建立4个分类器：逻辑回归和三类惩罚逻辑回归（LASSO惩罚逻辑回归，L2惩罚逻辑回归和弹性网惩罚逻辑回归），用训练数据学习分类模型，再用测试集中的观察值X预测响应变量Y的发生概率，接着选取最佳阈值c确定预测值Ŷ，最后由所有样本和预测结果得混淆矩阵、灵敏度和特异度，绘制ROC曲线得到AUC评价不同分类模型的预测精度。LASSO惩罚逻辑回归、L2惩罚逻辑回归和弹性网惩罚逻辑回归分别是对逻辑回归施加L1惩罚、L2惩罚和弹性网惩罚（介于L1惩罚与L2惩罚之间）。比较4个分类器的预测结果可知，LASSO惩罚逻辑回归的预测表现最好，预测精度达到97.18%；弹性网惩罚逻辑回归的预测表现随着α的增大发生变化，特别当α=0.9时，弹性网惩罚逻辑回归的预测精度达到97.18%，与LAS⁃SO惩罚逻辑回归的预测表现一样好；L2惩罚逻辑回归的预测表现排第3；逻辑回归的预测表现最差。因此，本文提出的LASSO惩罚逻辑回归方法和弹性网惩罚逻辑回归方法可以有效预测乳腺癌，提高诊断精度。

1 数据来源与预处理

本文分析569例乳腺癌患者诊断数据，包含10个特征。数据来自威斯康星大学UCI网站（https：//archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29）。原始数据是569行32列的表格：第1列是患者的ID编号，第2列是诊断结果：良性（Benign）或恶性（Malignant），第3~32列是10个特征的3种值：前10列分别对应10个特征中每个特征的平均值，中间10列分别对应10个特征中每个特征值的标准差，后10列分别对应10个特征中每个特征值的最大值（即特征值前3名的平均值，可减弱计算误差带来的影响），其中特征值描述样本图像中细胞核的形态特征，主要通过乳腺肿块的细针穿刺（Fine needle aspiration，FNA）［20］数字化图像计算得到。从诊断结果看，在569例乳腺癌患者中，良性357例，恶性212例，良性占比62.7%，恶性占比37.3%，两个类不算失衡（一般两个类的比值为9∶1表示失衡，比值为99∶1表示严重失衡）。本文选取数据集中细胞核特征值的平均值（均值体现样本细胞核的总体形态特征）进行分析，表1详细介绍了数据涉及的预测变量。

表1 10个预测变量Table 1 Ten prediction variables

表1中每个指标分别从不同方面刻画肿瘤细胞核的特征，这些特征有助于医生诊断肿瘤是恶性还是良性。表2列举了10个预测变量的重要描述统计量。

由表2可看出，细胞核的半径、纹理、周长和面积的最小值和最大值相差较大，说明良性与恶性肿瘤细胞有明显差异；细胞核的半径和纹理两个变量的均值和中位数比较接近，且与方差和标准差也比较接近，说明数据波动不大；细胞核的周长和面积两个变量的方差及标准差都比较大，数据波动大。其余6个指标的方差和标准差都非常小，说明数值波动小，比较稳定，且它们的均值和中位数相当接近，指标值在最小值和最大值之间的波动也很小。表2中10个预测变量存在相关关系，这里借助corrplot包对相关系数输出结果作可视化处理，得到如图1所示的相关系数矩阵。

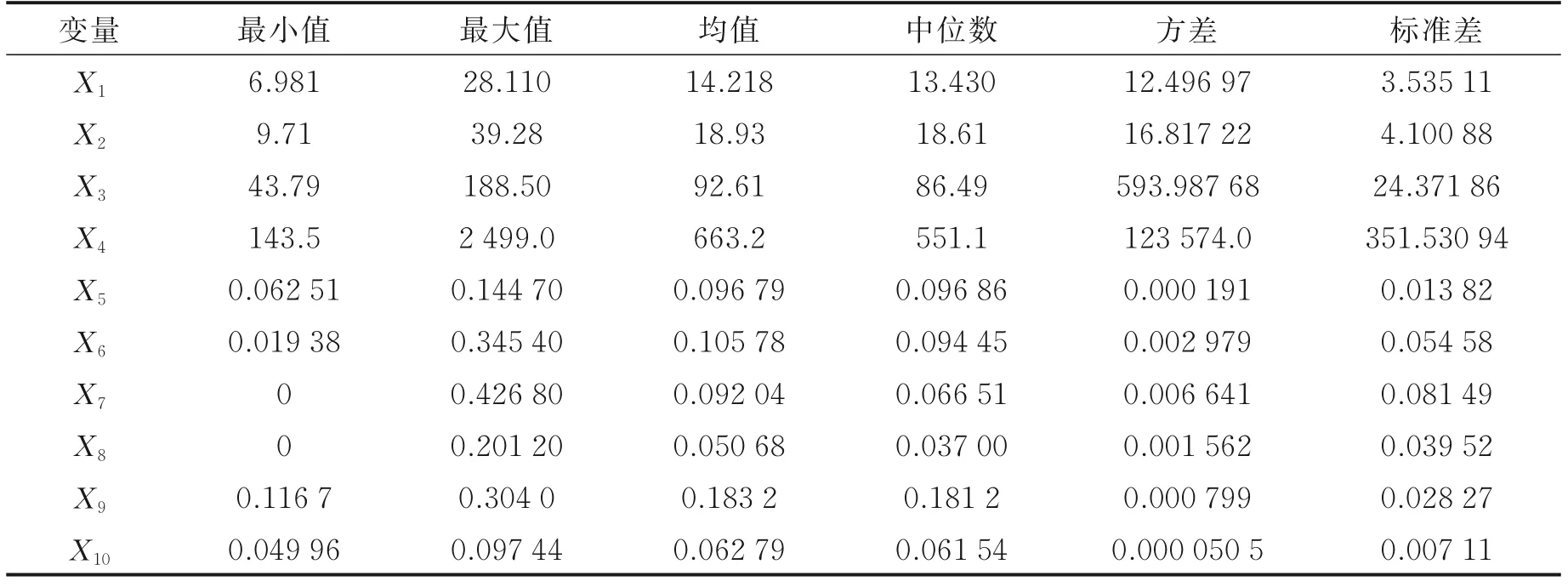
表2 10个预测变量的描述统计量Table 2 Descriptive statistics for 10 prediction variables

图1中圆圈越大代表相关性（包括正相关和负相关）越强。观察图1可知，细胞核的紧密程度与凹度和凹点的相关系数分别为0.89和0.84，具有强相关性；细胞核的凹度与凹点的相关系数为0.92，也具有强相关性；细胞核的周长、面积与半径的相关系数接近1，具有更强的相关性；而数字化图像中细胞核之间的似圆度有差异，不能完全确定其相关关系，故分成两个特征指标计算。表3列出了预测变量与响应变量之间的相关系数。

表3 预测变量与响应变量之间的相关系数Table 3 Correlation coefficients between prediction variables and response variables

图1 10个预测变量的相关系数矩阵图Fig.1 Correlation coefficient matrix for ten prediction variables

显然，这些预测指标存在相关性，考虑到医学诊断的特殊性，本文没有对这些相关指标作进一步处理。本文数据预处理如下：先将患者的诊断结果B和M重新编码为0和1（0表示良性，1表示恶性），再对数据集的10个预测变量作标准化处理，最后将数据集分为75%的训练集和25%的测试集，其中训练集用来学习分类模型，测试集用来检验模型的预测精度。下面利用逻辑回归与LASSO惩罚、L2惩罚、弹性网惩罚3种惩罚逻辑回归预测乳腺肿瘤的良性与恶性，协助临床医生诊断患者肿瘤状态，减少误诊，提升诊断效率，进而提升乳腺癌患者的治愈率和存活率。

2 四种分类器

2.1 逻辑回归

逻辑回归模型是一种广义回归模型，常用于预测分类问题。二类逻辑回归（Logistic regression，LR）表示为

2.2 LASSO惩罚逻辑回归

LASSO惩罚是Tibshirani［21］于1996年提出的一种变量选择和收缩估计方法，主要对线性回归引入一个L1惩罚函数（回归系数的绝对值之和小于调整参数）得到LASSO惩罚线性回归。本文的LASSO惩罚逻辑回归主要利用训练样本得到逻辑回归的负对数似然函数，并引入一个L1惩罚，作变量选择的同时得到模型参数估计，再结合检验样本预测分类。LASSO惩罚逻辑回归的估计可以表示为

式中ℓ(β)见式（5）。式（14）中系数的惩罚力度主要由调节参数λ决定并控制模型的拟合优度。当λ=0时，对应没有惩罚的逻辑回归，估计为极大似然估计；当λ增大，系数估计的压缩越大，特别当λ→∞时，所有系数都被压缩为0。

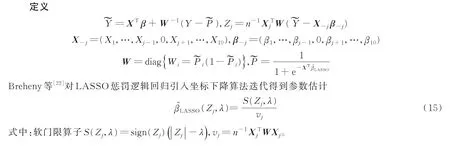
2.3 L2惩罚逻辑回归

与LASSO惩罚逻辑回归不同，L2惩罚逻辑回归是对逻辑回归的负对数似然函数引入L2惩罚函数实现变量选择和回归系数收缩的目的。对应的惩罚似然函数为［23］

2.4 弹性网惩罚逻辑回归

Zou等［24］提出了弹性网（Elastic net，EN）惩罚方法。该方法是L1惩罚和L2惩罚的折中，适合p≫n的超高维稀疏情况和具有多重共线性的模型。由于对逻辑回归引入弹性网惩罚可改进模型表现，减少预测误差，因此这里对逻辑回归的负对数似然函数引入弹性网惩罚，得到弹性网惩罚逻辑回归及其模型估计。

当α=0时，弹性网惩罚逻辑回归为L2惩罚逻辑回归；当α=1时，弹性网惩罚逻辑回归为LASSO惩罚逻辑回归。因此弹性网惩罚结合了LASSO惩罚与L2惩罚的优点，既能进行变量选择又能消除共线性影响。

3 模型精度评估

3.1 混淆矩阵

常用混淆矩阵和ROC曲线评估预测精度。混淆矩阵分别对真实分类序列和预测分类序列统计分类模型归错类与归对类的观测值个数。本文借助caret包中的confusionMatrix函数来计算混淆矩阵。如果0表示良性，1表示恶性，则二分类混淆矩阵如表4所示。

表4 二分类混淆矩阵Table 4 Binary confusion matrix

下面利用混淆矩阵计算准确率、精确率、错误率、灵敏度和特异度等指标。

准确率（Accuracy）表示模型预测结果正确的样本数与所有样本数的比值，即

这些指标无法直观判断模型效果，因此利用特异度和灵敏度两个指标绘制ROC曲线：1-特异度为x轴，表示假阳性率（False postive rate，FPR），FPR越小，误判率越低，预测正类中实际负类越小；灵敏度为y轴，表示真阳性率（True postive rate，TPR），TPR越大，命中率越高，预测正类中实际正类越多。绘制不同阈值下1-特异度和灵敏度的组合变化，ROC曲线下的阴影面积就是AUC指标。通常AUC的值越大，模型拟合效果越好。本文利用p ROC包实现ROC曲线的可视化，用glmnet包构建逻辑回归、惩罚逻辑回归在坐标下降算法下的正则化路径。

3.2 几种模型的预测表现

利用乳腺癌数据集建立逻辑回归，求出各个预测变量对应的参数估计值，结果如表5所示。

表5 逻辑回归模型的参数估计值Table 5 Parameter estimation for logistic regres⁃sion model

从表5中看出显著变量并不多，但不显著变量对诊断结果也不是完全没有影响。这里用逐步回归作变量选择，结果如表6所示。

从表6看出选出的变量显著，比较两个度量模型拟合优度（Akaike information criterion，AIC）结果，包含全部变量的模型AIC=130.13，变量选择后的模型AIC=120.66，AIC值越低的模型效果更好，因此通过变量选择提升了模型效果。通过变量选择，效果明显变化的是变量X4和X8，β̂4从13.035 94上升到14.860 0，其P值从0.062 18下降到0.014 147，变得更加显著；β̂8从2.380 43上升到2.522 8，其P值从0.071 67下降到0.000 123，显著性明显提高。因此，变量选择后的预测模型为

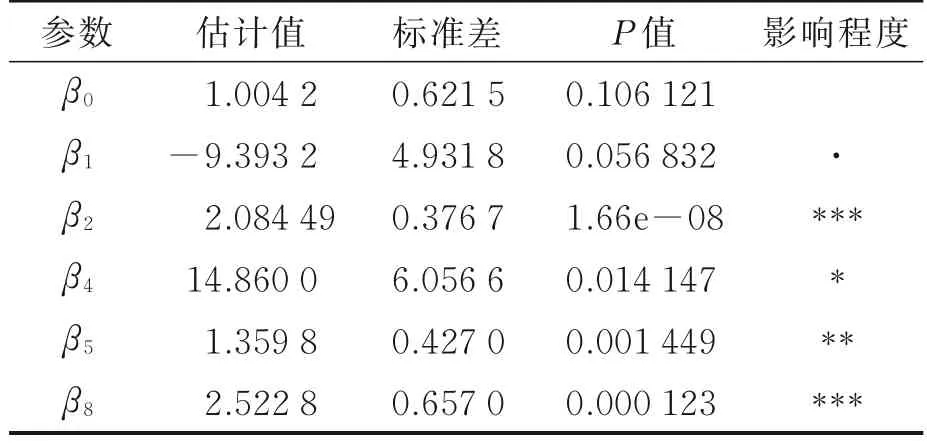
表6 变量选择后的参数估计值Table 6 Parameter estimation after variable selec⁃tion

由以上模型得出，X1每增加1个单位，相应的优势比对数减少9.393 2，即乳腺肿瘤细胞核的半径与肿瘤是良性还是恶性呈负相关；X2每增加1个单位，相应的优势比增加2.084 49，即乳腺肿瘤细胞核的纹理与肿瘤是良性还是恶性呈正相关；其余的X4、X5、X8皆呈现正相关性。

利用75%的训练集数据学习预测模型，利用25%的测试集数据建立混淆矩阵和ROC曲线图检验模型预测效果。先设定一个阈值，将概率值大于这个阈值的归为1类，小于这个阈值的归为0类。最佳阈值的选取会直接影响模型预测结果，这里将预测值和实际值从低到高排序放在一起，在0和1分界值的区间中选取最佳阈值，先设定区间中的一个值得出ROC曲线图，得到最佳阈值和特异度、灵敏度等值，再根据这个阈值调整使得设定的阈值与ROC得到的最佳阈值一致，即为最终的最佳阈值。

利用10个预测变量和响应变量建模LASSO惩罚逻辑回归，用十重交叉验证选取模型，对于每一个λ值，在红点所示目标参量的均值左右，可以得到一个目标参量的置信区间。两条虚线分别指示了两个特殊的λ值：一个是lambda.min，即给出最小交叉核实误差的λ值；另一个是lambda.1se，即给出交叉核实误差最小值的1倍标准差范围的λ值。通过选取模型准确性较高的λ作为调节参数，得到LASSO惩罚逻辑回归的混淆矩阵。对逻辑回归引入L2惩罚得到L2惩罚逻辑回归。将LASSO惩罚和L2惩罚进行折中得到弹性网惩罚，并选取3组不同值进行分析（α=0.3、0.5、0.9），得到不同模型的混淆矩阵，结果如表7所示。

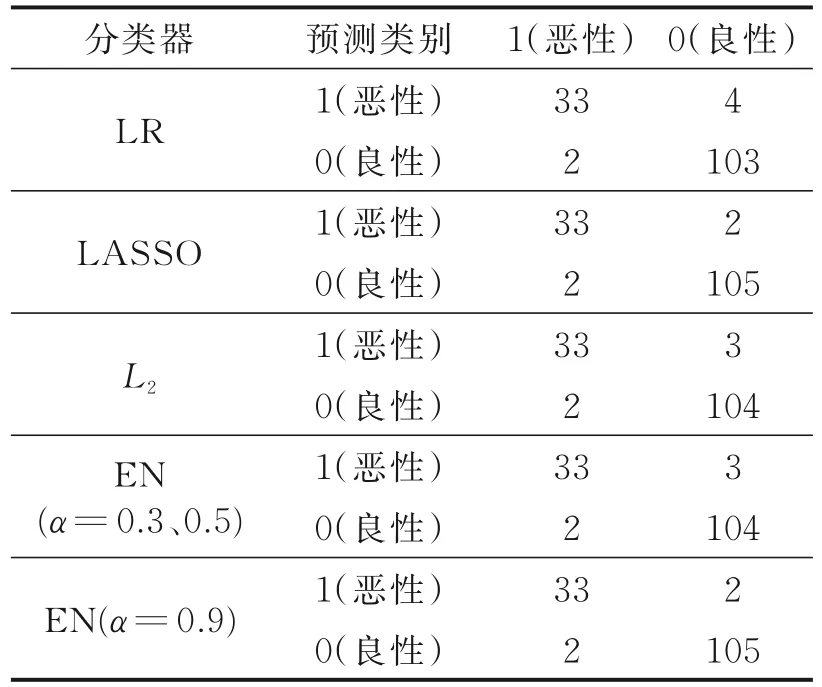
表7 混淆矩阵Table 7 Confusion matrix

由表8可得模型的预测准确率，α=0.3和α=0.5时的弹性网与L2惩罚逻辑回归的计算结果一致，α=0.9时的弹性网惩罚与LASSO惩罚的结果一致，且每种模型的灵敏度都为0.942 9。初步判断模型的预测效果，逻辑回归的准确率为0.957 7；LASSO惩罚逻辑回归的准确率为0.971 8；L2惩罚逻辑回归的准确率为0.964 8；弹性网惩罚逻辑回归对于不同的α值，预测表现也不同，其最佳预测准确率为0.971 8。因此，惩罚逻辑回归模型预测表现优于不加惩罚的逻辑回归模型。

表8 通过混淆矩阵计算的指标值Table 8 Index values calculated by confusion matrix

ROC曲线图可直观评价预测效果，主要依据折线下AUC的值，AUC越大，分类器预测表现越好。AUC的取值范围在0.5和1之间，越接近1的预测效果越好，当AUC=0.5时，分类器基本不起作用，预测结果和随机猜测差不多；AUC在0.5~0.7时有较低准确性；AUC在0.7~0.9时有一定准确性；AUC在0.9以上有较高准确性。利用灵敏度和特异度绘制ROC曲线图如图2所示。

图2 几种模型的ROC曲线Fig.2 ROC curves for several models

由图2可直接得到模型的最佳阈值、灵敏度、特异度和AUC值，结果如表9所示。

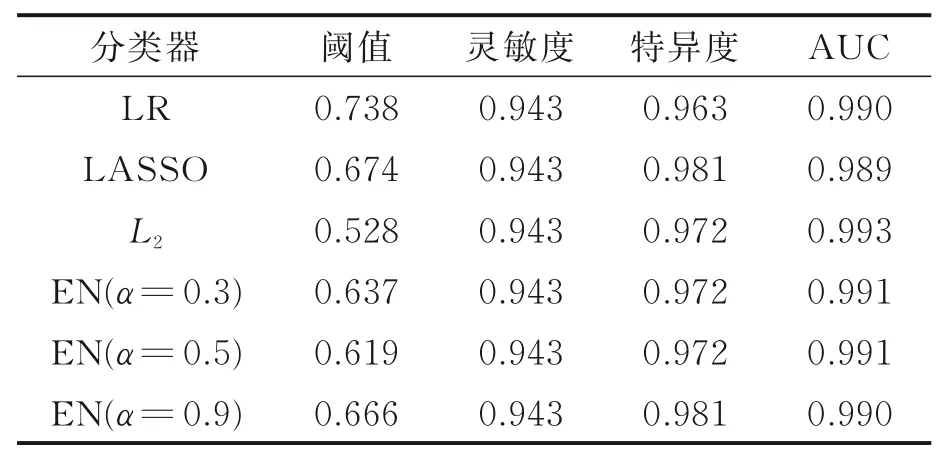
表9 通过ROC曲线得出的指标值Table 9 Index values derived by ROC curves

由表9可知，ROC曲线得出的灵敏度和特异度与混淆矩阵计算值一致，其中LASSO和α=0.9的弹性网惩罚逻辑回归具有相同的精确率0.942 9，灵敏度0.942 9，特异度0.981 3。表9中逻辑回归的AUC=0.990；LASSO惩罚逻辑回归的AUC=0.989；L2惩罚逻辑回归的AUC=0.993；弹性网惩罚逻辑回归α=0.9时的AUC=0.990，故分类器预测表现不错。

4 结束语

本文利用威斯康星大学的数据来学习不同分类模型，利用指标平均值作为预测变量建立4种分类器：逻辑回归、LASSO惩罚逻辑回归、L2惩罚逻辑回归和弹性网惩罚逻辑回归预测乳腺癌，展示了不同的预测表现和预测精度，其中LASSO惩罚逻辑回归分类器和弹性网惩罚逻辑回归分类器预测表现更好，预测精度最高，逻辑回归预测表现最差，预测精度最低。本文收集的数据样本量不大，下一步重点研究如何在大数据集中采用这些分类器进一步提高乳腺癌的预测表现。