基于加权和RSSI测距的DV‑Hop定位算法

吴之舟，张玲华

（南京邮电大学通信与信息工程学院，南京 210023）

引 言

无线传感器网络（Wireless sensor network，WSN）拓展了人类与物理世界的交互方式，是近20年通信技术发展的一个新研究领域，基于其成本低、功耗低和环境要求低的优点，在工业、农业和商业中都有着广泛的应用。在这个巨大的无线网络中，可以说没有节点定位就没有传感器网络。因此，在组成WSN的各种技术中，定位技术是最关键技术之一［1］。

定位算法分为基于测距和非测距两类［2］，基于测距的定位算法主要有到达时间（Time of arrival，TOA）、到达时间差（Time difference on arrival，TDOA）和接收信号强度（Received signal strength indica⁃tor，RSSI）等。其中TOA和TDOA是以获得测量距离为前提的算法，具有相对较高的定位精度，但是对硬件的要求很高，成本高并且受到测距技术的限制。而RSSI算法是通过节点间的信号强度来估算未知节点，因此它无须额外硬件开销，但是在信号传播中对环境、地形因素要求较高，定位精度受到信道衰弱、多径效应的影响较大。相比之下，非测距定位算法是利用节点间估计距离来计算未知节点，主要 算 法 有 质 心 算 法、近 似 三 角 形 内 点 测 试 法（Approximate point⁃in⁃triangulation test，APIT）及DV⁃Hop［3］等。非测距方法的成本和功耗低，但是定位误差大，这两类定位算法可以说各有优缺点。因此，众多学者针对DV⁃Hop定位算法展开研究并取得了一些理论成果。文献［4］通过定义理想跳数、偏差系数和修正因子来改进跳数，在一种全新的极值更新方式的基础上提出了改进粒子群算法，并用于计算未知节点坐标，有效提高了定位精度。文献［5］借助划分多个通信半径的方法来优化平均跳距，并利用模拟退火算法来降低定位误差。文献［6］在DV⁃Hop算法改进中引入了RSSI技术，通过对数⁃常态分布模型来定义锚节点的平均跳距误差，使得锚节点和未知节点间估算距离更精确，这种改进方法可以在不增加硬件损耗的基础上有效提高定位精度，但在算法中依然存在改进的余地。

本文改进了传统DV⁃Hop［4］算法的3个步骤：首先利用多通信半径的方法修正最小跳数，对计算出的平均跳距进行加权归一化处理；然后用RSSI测得的距离与欧氏距离的差定义每个锚节点的平均跳距误差，乘以跳数后，再加上加权后的估计距离，使得未知节点与锚节点之间的估计距离误差更小；最后采用加权最小二乘法估算未知节点坐标。研究表明，改进后的算法精度较高，有效减少了定位误差，并且在节点数量较少时依然能发挥良好作用。

1 传统DV‑Hop算法

1.1 具体步骤

DV⁃Hop算法的起源是距离矢量路由协议［5］，它的定位过程分为3步。

第1步计算最小跳数［6］。在规定区域内随机不规则部署所有节点，信标节点通过信息广播的方式发送数据包给相邻节点，相邻节点比较多个跳数信息后记录最小跳数。

第2步估算节点间距离。根据锚节点间最小跳数和坐标，估算出平均跳距为

式中：(xi，yi)为锚节点i的坐标；hiu为锚节点i和u间的最小跳数。

估算未知节点j到锚节点i的距离为

第3步最大似然估计法求节点坐标。由式（2）可得

式中dn为未知节点(x，y)与锚节点间的欧式距离。

在进行相减后，对线性方程组用矩阵表示为

式中

式中：矩阵A为实矩阵；矩阵X为未知节点坐标矩阵；ATA可逆，因此由式（3）转化的线性方程组总是有解的，可以解得矩阵X。

1.2 DV‑Hop算法误差分析

（1）最小跳数存在误差。节点在网络中的分布是随机且不规则的。因此在某一个锚节点的一个通信半径所围成的圆形区域内，节点间距离一般是随机的，即距离不等。按照传统DV⁃Hop算法来计算跳数时，节点间跳数相同，但是距离不等，导致误差出现。因此为了降低误差，应该采用划分多个通信半径的方法，而不能直接地将跳数值记为1跳。

（2）平均跳距［7⁃8］存在误差。因为节点是随机分布的，所以形成的网络拓扑结构不规则，2个节点需要经过多跳且非直线路径才能够实现通信。这种情况下，根据传统DV⁃Hop算法估计出的平均跳距小于真实跳距，造成定位精度降低。为了尽量修正误差，本文使用了加权平均跳距和RSSI测距修正估计距离的方法来减小误差。加权方法不会增加时间复杂度，而RSSI测距有着硬件成本低的特点，比较适合使用。

（3）坐标估算存在误差。DV⁃Hop算法中选择使用的计算方法，如三边测量法和最大似然估计法［9⁃10］等传统算法会加大定位误差。而文献中的一些智能优化算法，如粒子群算法、模拟退火算法等，虽然能取得更好的定位精度，但提高了算法复杂度和节点能耗，故本文采用加权最小二乘法，在不增加复杂度的前提下优化定位精度。

2 改进算法

2.1 多通信半径优化最小跳数

为了节约计算成本，本文划分了4个通信半径［11］，即将通信半径R划为4等分。网络中的锚节点通过泛洪的方式分为4次广播锚节点自身的坐标，这4次广播分别以通信半径为0.25 R、0.5 R、0.75 R和R进行。

第1次广播，锚节点以0.25 R为通信半径向相邻节点发送分组信息，此时相邻节点记录最小跳数为0.25，并且停止信息转发，以减小通信开销。第2、3和4次广播，通信半径和最小跳数都以0.25单位为间隔递增，多次重复操作，最终网络中的每个节点就能获得最小跳数。设相邻节点的实际距离为d，节点间的跳数hij为

2.2 加权平均跳距

计算估计距离为

式中：Wi为锚节点i的权值；HopsizeAvgj为未知节点j的加权平均跳距；d1ij为未知节点j到锚节点i的估计距离。

2.3 RSSI测距修正估计距离

本文采用对数⁃常态分布模型［12⁃13］来计算传播路径损耗，有

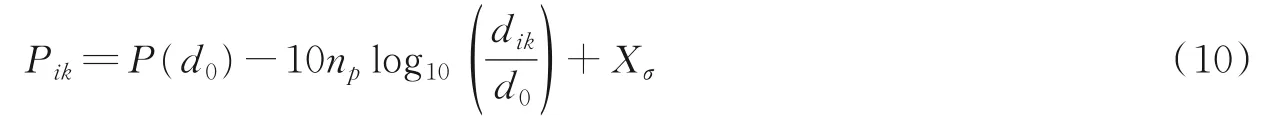
式中：Pik为锚节点i和k之间的接收信号强度，单位为d B·m；d0为信号参考传输距离；P(d0)为接收信号强度，取d0=1 m；np为衰减指数，一般取2；dik为锚节点i和k的欧氏距离；Xσ为均值是0、方差是σ（本文取10）的高斯随机分布，误差可忽略。

在实际应用中，可以通过多次获取同一锚节点的信号，降低RSSI带来的误差。接收信号强度Pik与距离成反比。图1为信号强度随距离变化关系。

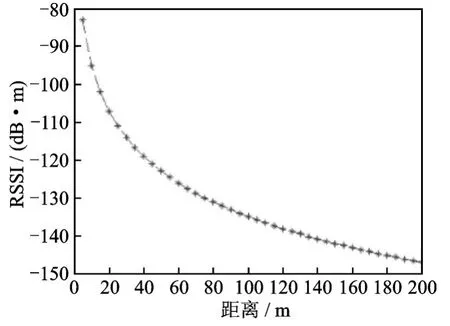
图1 信号强度随距离变化关系Fig.1 Relationship between signal strength and distance

由式（10）可推导出距离公式

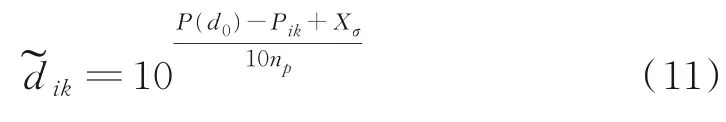
求得锚节点i的平均跳距误差ci和锚节点i和未知节点j的修正距离d2ij为

结合式（9，13），可得

式中：d2ij、dij为锚节点i和未知节点j的修正距离和估算距离。

2.4 加权最小二乘法

传统最大似然估计法的矩阵B中的各项元素会产生定位误差，这是由于各项元素的方差会随着坐标的变化而改变，即扰动项的方差不全相等，为了消除异方差性，有效减小定位误差，就需要采用加权二乘法代替最大似然估计法。

无线传感器网络通常资源有限，在提升定位精度的同时也要兼顾考虑算法的时间复杂度等其他因素。文献［12］中的基于模拟退火的粒子群优化算法（Simulated annealing particle swarm optimization al⁃gorithm，SAPSO）定位算法就是融合了改进粒子群算法和模拟退火算法，通过牺牲算法复杂度来换取定位精度，虽然这种方法对定位精度有较大的提升，但对无线传感器网络有巨大负担。根据文献［14］的研究，相比于其他改进算法，加权最小二乘法的时间复杂度与最大似然估计法近似相等并且能有效减小定位误差，因此从时间复杂度和定位精度方面综合考虑，就需要采用加权二乘法。

加权最小二乘法的原理是消除扰动项方差的不相等，即对偏离程度较大的数据乘以较小的权值，而对偏离程度较小的数据乘以较大的权值，最终使各项数据方差可以近似相等。因此，采用文献［9］中的改进双曲线定位算法模型可以实现更好的定位精度。

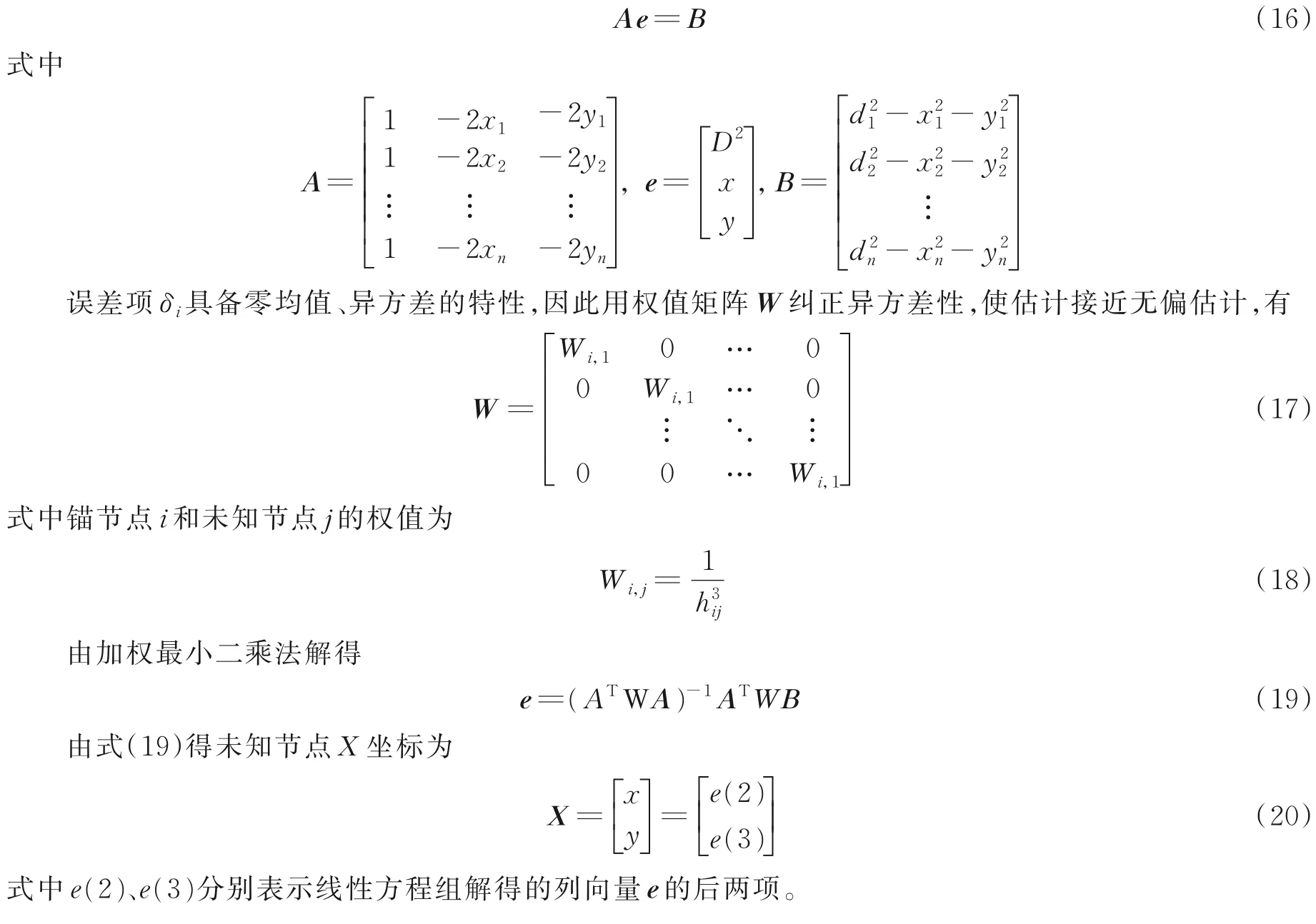
本文直接将式（3）展开，并且令D2=x2+y2，代入误差项δi，得

将D、x和y看作未知数，将式（15）的线性方程组的形式转变为矩阵形式

3 仿真结果分析

3.1 算法的定位精度分析

本文基于MATLAB软件进行仿真实验，仿真环境为100 m×100 m的二维区域。为了减小随机性带来的定位误差，仿真实验进行200次，并取平均值。

采用归一化定位误差在不同总节点个数、通信半径和锚节点密度的情况下比较算法定位性能，对比结果如图2~4所示。平均定位误差（Average positioning error，APE）计算公式［13］为

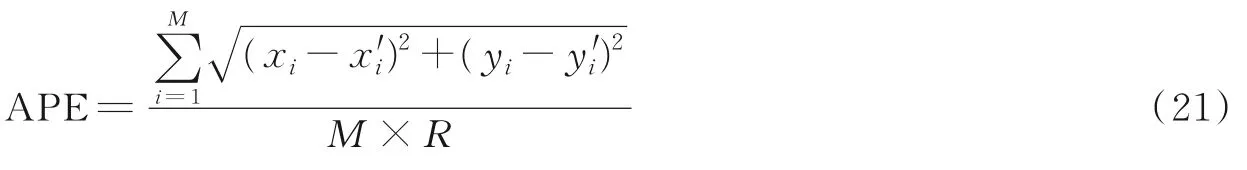
式中：M为未知节点个数；R代表通信半径；(xi，yi)为节点的真实坐标；(x'i，y'i)为节点的估计坐标。

图2~4中：Improved algorithm代表本文改进算法；DV⁃hop代表传统DV⁃Hop算法；DV⁃hop2代表文献［14］中通过加权最小二乘法优化的算法；DV⁃hop3代表文献［15］中提出的IDV⁃Hop+WH算法，它的改进基于平均修正系数和加权双曲线定位算法。

图2（a）给出了在锚节点占比为20%，通信半径为25 m，总节点个数以20为间隔从60增加至200的环境下4种算法的平均定位误差的变化；图2（b）给出了在锚节点占比为15%，通信半径为30 m，总节点个数以20为间隔从60增加至200的环境下4种算法的平均定位误差的变化。由图2可知，4种算法的平均定位误差都与节点总数成反比，但Improved algorithm的定位误差一直稳定最小。在总节点个数为60时，Improved algorithm算法的定位误差相对于DV⁃hop降低了0.17~0.18，相对于DV⁃hop2降低了0.11~0.15，相对于DV⁃hop3降低了0.02~0.06。由此可见，本文改进算法在节点数量比较少的区域中仍然可以保持较好的定位精度。图3（a）给出了在总节点个数为100，通信半径为25 m，锚节点密度以0.05为间隔从0.1增加至0.45的环境下4种算法的平均定位误差的变化；图3（b）给出了在总节点个数为80，通信半径为30 m，锚节点密度以0.05为间隔从0.1增加至0.45的环境下4种算法的平均定位误差的变化。由图3可知，当锚节点密度增加时，4种算法的平均定位误差都在降低，但Improved algorithm算法的工作效果始终是最佳的。Improved algorithm算法的定位误差相对于DV⁃hop降低了0.17~0.19，相对于DV⁃hop2降低了0.1~0.12，相对于DV⁃hop3降低了0.02~0.09，Improved algorithm算法曲线相对于其他3种算法更平滑一些，可以看出本文改进算法具有良好的稳定性。

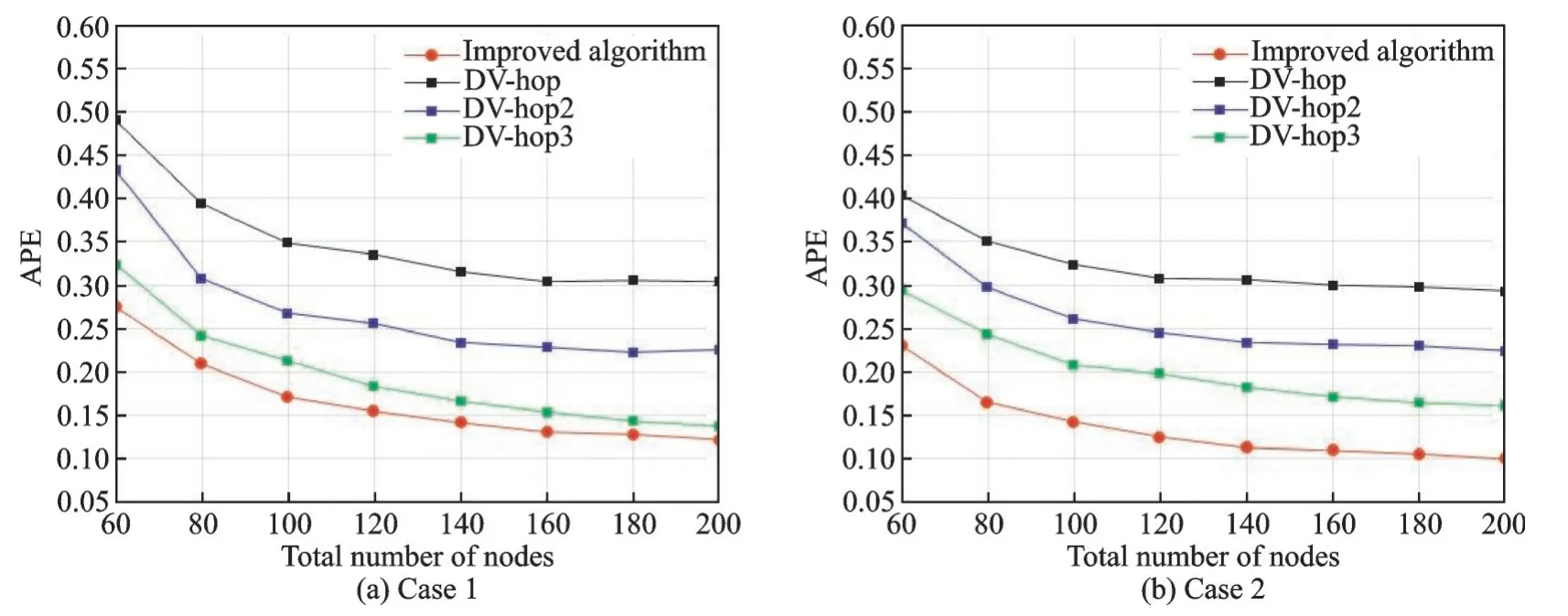
图2 不同总节点个数情况下算法性能比较Fig.2 Performance comparison with different numbers of total nodes

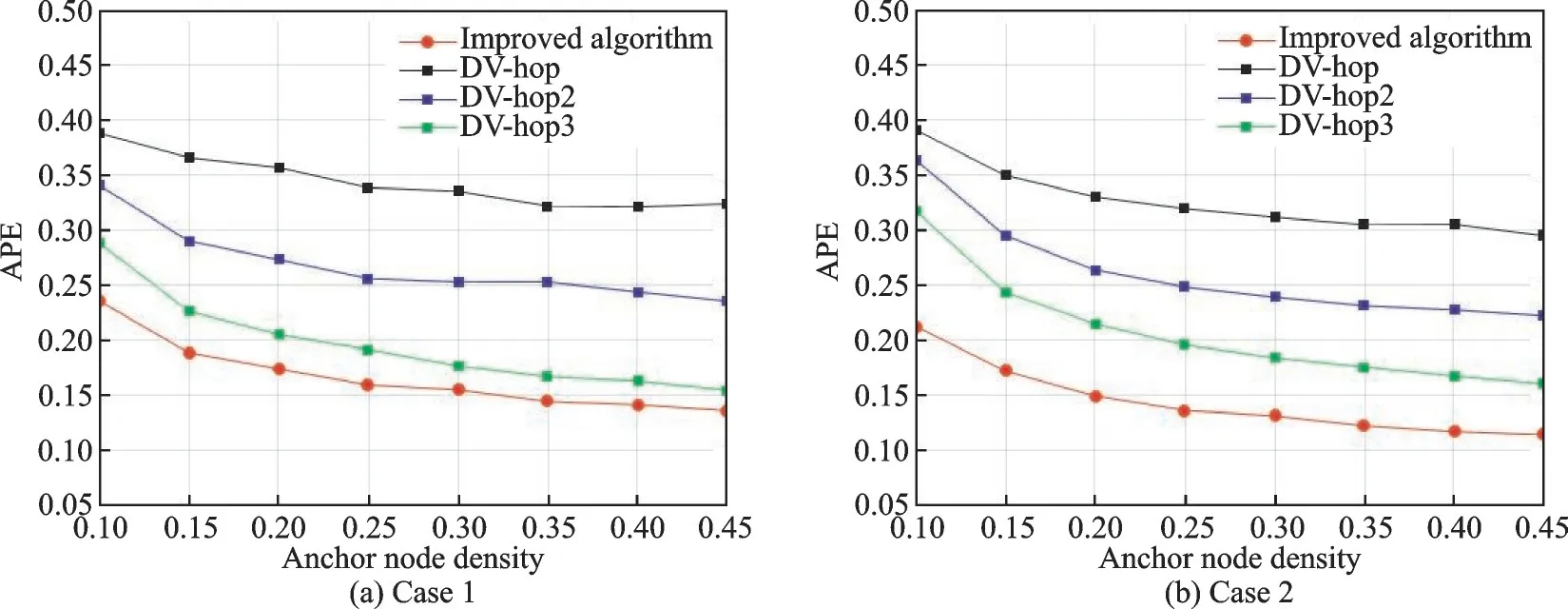
图3 不同锚节点密度情况下算法性能比较Fig.3 Performance comparison with different anchor node densities

图4（a）给出了在总节点个数为100，锚节点密度为20%，通信半径以5 m为间隔从15 m增加至50 m的环境下4种算法的平均定位误差的变化；图4（b）给出了在总节点个数为120，锚节点密度为10%，通信半径以5 m为间隔从15 m增加至50 m的环境下4种算法的平均定位误差的变化。由图4可知，尽管4种算法的定位误差随着网络连通性的提高而降低，但是Improved algorithm算法的误差始终低于其他两个改进算法，并且在趋于稳定时，改进算法的误差比传统算法减少约50%。由此可见，在通信半径大于35 m后，误差曲线近似水平，本文改进算法定位性能更好。

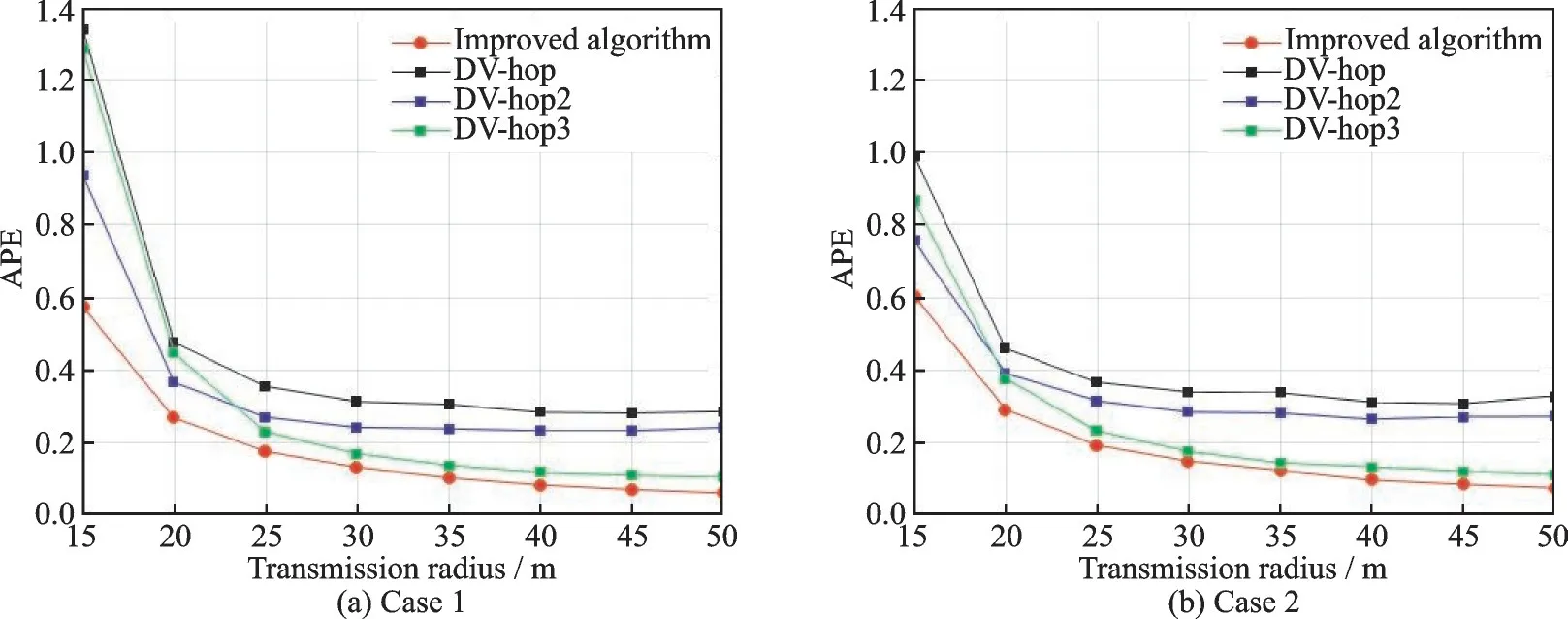
图4 不同通信半径情况下算法性能比较Fig.4 Performance comparison with different transmission radius

3.2 RSSI测距技术的影响分析

根据RSSI对数⁃常态分布模型，在同一通信半径下，每个锚节点的平均跳距误差近似一致，因此采用对平均跳距误差ci求均值的方法来确定在不同通信半径下的RSSI测距技术性能，平均跳距误差均值（Average hop⁃distance error，AHde）计算公式为

式中：N代表总节点个数；M代表仿真区域中未知节点个数；ci为锚节点i的平均跳距误差。

图5（a）给出了在总节点个数为100，锚节点密度为20%，通信半径以5 m为间隔从15 m增加至55 m的环境下，本文改进算法Improved algorithm在不同通信半径下的平均跳距误差均值AHde变化。由图5（a）可得，在通信半径增大的过程中，平均跳距误差和通信半径近似成正比例关系，即通信半径越大，跳距误差也越大。

图5（b）给出了在总节点个数为100，锚节点密度为20%，通信半径以5 m为间隔从15 m增加至55 m的环境下，Nonerssi算法和Improved algorithm算法的平均定位误差的变化，其中前者是不采用RSSI测距的本文改进算法。由图5（b）可知，当通信半径为15~35 m之间时，两种算法的定位误差近似一致；当通信半径调整到大于35 m之后，Improved algorithm算法的定位误差下降趋势逐渐平缓但依然在降低，并且始终低于Nonerssi算法。也就是说，通信半径在超过35 m之后，RSSI测距技术修正平均跳距的效果更为突出。

图5 跳距误差和定位误差随通信半径变化关系Fig.5 Relationship between hop error and positioning error with communication radius

3.3 时间复杂度分析

设随机分布的总节点个数为n，则传统DV⁃Hop算法中，利用最小二乘法计算未知节点坐标的时间复杂度为O(n4)。本文改进算法的时间复杂度在传统算法的基础上增加了O(n)，这是因为在仿真中需要用对数⁃常态分布模型来模拟接收信号强度RSSI，因此利用RSSI测距技术造成了较大的时间复杂度。但是在实际中几乎所有的节点都具有接收信号强度RSSI的功能，可直接获得RSSI值，因此时间复杂度增加不大，但定位精度得到了较好的改善。

4 结束语

为了改进传统DV⁃Hop算法的3个步骤存在的误差问题，首先利用多通信半径细化节点间的跳数，再采用RSSI测距和加权归一化优化跳距，最后采用加权最小二乘法修正误差项的异方差性。通过仿真结果表明，本文改进算法Improved algorithm相比于传统DV⁃Hop算法、DV⁃hop2、DV⁃hop3的定位精度提升了约53%、31%和12%，改进算法的定位精度有明显提高；在总节点数较少时依然能有效定位，有着良好的稳定性；没有消耗时间复杂度来提升定位精度，时间复杂度与传统算法相差不大。然而，本文算法依然存在可以改进的内容，比如考虑在三维空间内通信过程受障碍物的影响等问题，所以下一步将拓展到三维空间中进行研究。