基于无迹卡尔曼滤波的无人机毫米波波束跟踪算法

李鹏辉，仲伟志，张璐璐，杨卓明，朱秋明，陈小敏

（1.南京航空航天大学航天学院，南京 210016；2.南京航空航天大学电子信息工程学院，南京 211106）

引 言

近年来，无人机（Unmanned aerial vehicle，UAV）因为具有成本低、灵活性强和覆盖面积广等优点，被认为是第5代（5th⁃Generation，5G）通信网络中各种应用场景的承载者，例如，作为足球比赛、音乐会等短时间高密度聚集人群的飞行基站，为人们提供无线覆盖；在自然灾害期间提供额外的通信容量帮助恢复通信系统［1⁃2］等。

无人机应用场景越多，执行的任务越复杂，无人机需要的数据吞吐量也越多。因此，拥有巨大免许可连续带宽的毫米波频段（30~300 GHz），得到无人机通信领域的广泛关注［3⁃5］。然而，毫米波由于频率较高，导致路径损耗较大，尤其在降雨等天气下会产生极大衰减［6］。因此，研究者提出采用大规模阵列天线下的波束成形技术的方法来弥补毫米波传播中的路径损耗［7⁃8］。由于该技术依靠特定方向上的高增益窄波束进行通信，无人机和用户间的相对运动会导致波束失配，影响通信质量。为了保证正常稳定的通信效果，需要不断调整收发端的波束角度，实现波束的实时对齐。因此，有效的波束跟踪方法对于将毫米波应用在无人机通信领域中具有重要意义。

以往，针对毫米波波束跟踪这一问题的研究相对较少。文献［9⁃10］通过训练波束进行跟踪，其中波束方向被周期性地训练以保持波束对准。但由于环境复杂，训练频率需要足够高才能应对。文献［11］提出基于波束相干时间调整训练频率，因此当角度变化不快时，可以降低开销。但仍然不适合快速移动变化场景。文献［12］提出的波束跟踪方法是在数据包中附加训练序列以检测信号强度。这种方法需要训练多个波束对，因此开销较大。文献［13］采用扩展卡尔曼滤波（Extended Kalman filter，EKF）算法进行波束跟踪，该算法通过扫描所有可能的波束组合，建立EKF算法中的测量矩阵，完成波束跟踪。但文献［13］中的方法需要进行波束全扫描，导致测量时间较长，很难在快速变化的场景中进行波束实时跟踪。文献［14］将EKF算法应用于常规地面毫米波的波束跟踪。相比于文献［13］，文献［14］只需要训练一个波束，因此，大大降低了开销。同时文献［14］克服了文献［13］的缺点，在每个步骤中只使用一个测量方程，更加适合快速移动场景下的波束跟踪。由于文献［13⁃14］采用的EKF是通过对非线性系统的一阶线性化来解决非线性状态跟踪问题的，这会在线性化的真实后验均值和协方差中引入较大误差，导致滤波器的次优性能，有时还会出现滤波器发散［15］。此外，文献［13⁃14］使用的是均匀线性天线阵列，并且只对一个角度进行二维跟踪，而无人机波束跟踪场景下，需要对两个角度进行三维波束跟踪。

针对上述问题，本文采用一种基于无迹卡尔曼滤波（Unscented Kalman filter，UKF）的毫米波波束跟踪方案。该方法利用UKF对收发波束角度进行跟踪，在收发两端均采用均匀平面天线阵列。UKF不需要对非线性函数进行线性化，没有忽略高阶项，因此对于非线性分布具有较高的计算精度，从而有效地提高了三维波束的跟踪精度。

1 传输系统模型

本文假设系统由一架无人机空中基站和一个地面用户组成。无人机作为发射机，向作为接收机的用户提供服务。本文假设系统传输只需要一个射频（Radio frequency，RF）链，系统模型如图1所示［16］。无人机和用户分别配备一个具有Mt×Nt、Mr×Nr根天线数的均匀平面阵（Uniform planar array，UPA），阵列天线间距为半波长。放置在x y平面内的均匀平面阵如图2所示。其中φ为方位角，θ为俯仰角，随着无人机和用户之间的相对运动，φ和θ会不断改变。本文使用θt和φt表示发射信号的俯仰角（Elevation an⁃gle of departure，EOD）和发射信号的方位角（Azimuth angle of departure，ZOD），θr和φr表示接收信号的俯仰角（Elevation angle of arrival，EOA）和接收信号的方位角（Azimuth angle of arrival，ZOA）。

图1 模拟波束成形系统Fig.1 Analog beamforming system

图2 在x y平面内矩形排列的均匀平面阵Fig.2 Uniform planar array with rectangular arrange⁃ment in x y plane

本文采用缓慢时变信道，在第k个时刻，其信道状态参数可以表示为

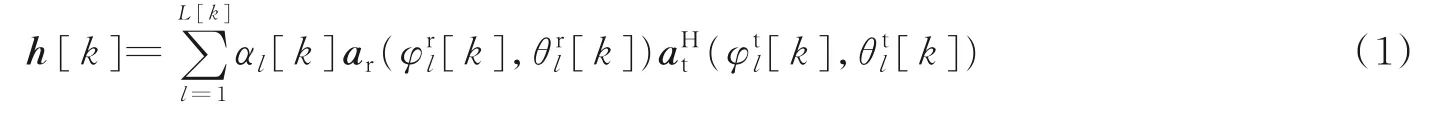
式中：L[k]为路径数量，αl[k]为第l条路径的复增益系数分别为第l条路径在第k时刻的EOA和ZOA，分别为第l条路径在第k时刻的EOD和ZOD，分别为第l条路径对应的接收端和发射端的阵列响应向量。由于在接收端和发送端均采用均匀平面阵，因此，阵列响应向量可表示为

式中：ξ=sinθsinφ，τ=sinθcosφ，“⊗”为克罗内克积，d为阵元间距，λ为载波波长，M和N为均匀平面阵的天线数目。

由于毫米波信号的大部分能量都是靠直视路径传播［4，17］的，因此式（1）可以简化为

发射端通过波束成形向量f发送导频符号s，为便于计算，设s=1，接收端波束合并向量为w，则在第k个时刻接收到的信号可以表示为

式中，w和f分别可以表示为

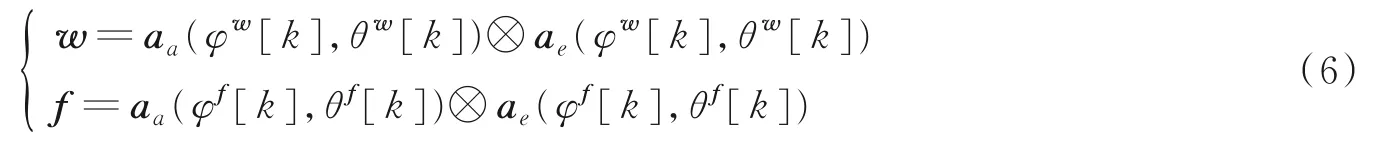
为便于使用UKF，这里定义一个包含方位角和俯仰角的状态向量

式中：u[k-1]为高斯过程噪声，u[k]~NC(0，Σu)，Σu=σ2I4。σ2表示收发端方位角、俯仰角的角度变化方差，这里假设收发端的方位角、俯仰角的方差相同（可以取不同的值）。这个参数决定了信道变化的速度，可以通过改变该参数的值来模拟不同信道变化速度下的情况。

2 基于UKF的波束跟踪算法

针对以往波束跟踪算法的不足，本文采用UKF算法来进行波束跟踪。该算法摒弃了对非线性函数进行线性化的传统做法，即在卡尔曼线性滤波框架下，对一步预测方程采用无迹变换来解决均值和协方差的非线性传递［15］，因此，可以提高无人机三维动态环境下波束跟踪的实时性和精确性。

2.1 无迹变换

无迹变换（Unscented transform，UT）是按一定规则在原状态中选取采样点集Xi[k|k]，又称作Sig⁃ma点集，采样点集的均值和协方差与原状态相等，然后将采样点集Xi[k|k]代入非线性函数，得到其对应函数值的点集Zi[(k+1)|k]，再利用这些点集求取变换后的均值Ẑ[(k+1)|k]和协方差PZZ[(k+1)|k]［15］。

本文采用基于对称分布采样的UT变换。设状态向量x[k]的采样点集为{Xi[k]}，i=0，…，2n，n是状态向量的维数，本文取n=4，则{Xi[k]}可表示为

式中：m和c分别表示均值和协方差；β为一个非负系数，其取值和状态向量x[k]的分布形式有关，对于高斯分布，取β=2较合适［18］。

2.2 UKF跟踪算法

三维UKF跟踪算法流程如图3所示，算法流程描述如下。

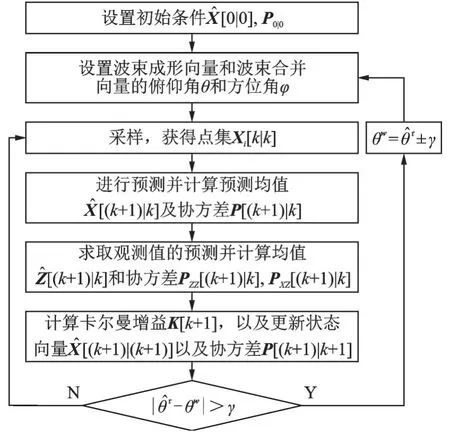
图3 三维UKF跟踪算法流程图Fig.3 Flow chart of 3D UKF tracking algorithm

步骤2获得采样点集。通过式（9，10）可获得[k|k]的一组采样点集Xi[k|k]及其对应的权值，其中，i=0，…，2n，n=4。

步骤3采样点一步预测。通过式（13）获得的状态方程，得到预测采样点Xi[(k+1)|k]。式（14，15）分别对预测采样点加权求和得到预测均值̂[(k+1)|k]以及协方差矩阵P[(k+1)|k]。具体预测过程为

式中Wi为式（10）获得的权值，在步骤2中已获得。

步骤4预测观测值。将预测采样点Xi[(k+1)|k]代入观测方程即式（16），求取预测观测值Zi[(k+1)|k]。通 过 式（18，19）得 到 预 测 观 测 值 的 均 值̂[(k+1)|k]和 协 方 差PZZ[(k+1)|k]、PXZ[(k+1)|k]。式（16）由式（5）得到。

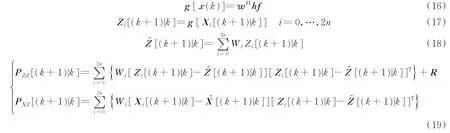
式中：R为式（5）中的测量噪声n[k]的协方差矩阵；n[k]为高斯白噪声。

步骤5状态更新。计算卡尔曼增益K[k+1]，更新状态向量̂[(k+1)|(k+1)]和协方差矩阵P[(k+1)|(k+1)]，具体步骤为

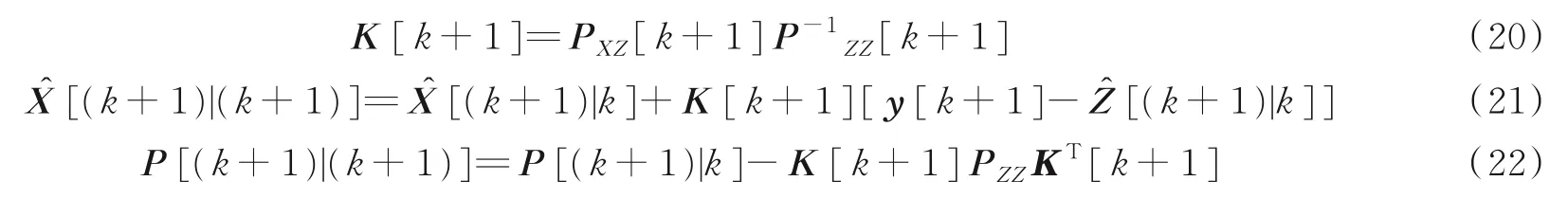
步骤6阈值判断。因为跟踪误差会随着时间逐渐积累，因此需要设置阈值γ来检测跟踪的有效性。当波束合并向量w和波束成形向量f的角度与UKF求得的最优估计值偏差超过阈值γ，即波束宽度的一半时，对两者的角度进行更新，否则继续跟踪。

在实际使用中，为了避免复数运算，对一些参数进行重新定义：[k]=[Re(y[k])，Im(y[k])]，[x(k)]=[Re(g[x(k)])，Im(g[x(k)])]，Re(⋅)和Im(⋅)分别为取实部和虚部，这样只需要计算实数。

3 仿真实验

为了验证UKF波束跟踪方法的性能，本文分别从信噪比（Signal to noise ratio，SNR）和阵列尺寸两方面对三维UKF跟踪算法进行仿真，并与文献［14］的EKF方法进行了对比。仿真参数设置如表1所示。

表1 仿真参数Table 1 Simulation parameters

3.1 信噪比

本节研究SNR对三维UKF跟踪方法的影响。图4显示了在不同SNR下的UKF跟踪的均方误差（Mean square er⁃ror，MSE）。实验中仿真参数的设置如下，收发端天线数Mr=Nr=Mt=Nt=16，角度变化方差σ2=(0.5°)2，仿真次数1 000次。

如图4所示，随着信噪比的增大，跟踪误差不断减小。3条曲线的区别为跟踪时隙的长度，随着跟踪时间的增长，所得到的均方误差不断增大，这表明UKF的跟踪效果受信噪比和跟踪时间长度影响较大。

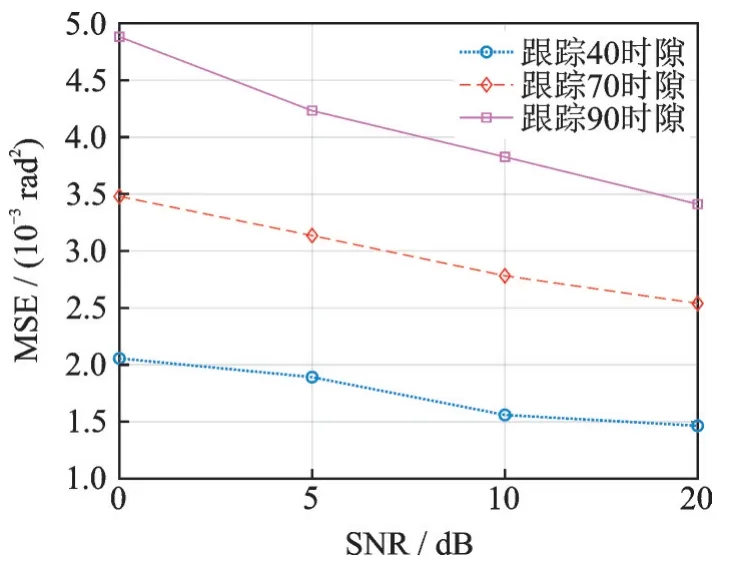
图4 不同SNR和跟踪时隙下的EOA的均方误差Fig.4 MSE of EOA with different SNRs and tracking slots

3.2 阵列尺寸

不同阵列尺寸下UKF算法的跟踪性能如图5和图6所示。仿真中，角度变化方差分别为σ2=(0.25°)2和σ2=(0.5°)2，SNR为20 dB，仿真次数为5 000次。

图5 不同阵列尺寸下的EOA的均方误差(σ2=(0.25°)2)Fig.5 MSE of EOA with different array sizes(σ2=(0.25°)2)

图6 不同阵列尺寸下的EOA的均方误差(σ2=(0.5°)2)Fig.6 MSE of EOA with different array sizes(σ2=(0.5°)2)

当σ2=(0.25°)2时，即角度变化较慢时，UPA⁃32×32的天线阵列跟踪性能最好；当σ2=(0.5°)2时，即角度变化较快时UPA⁃16×16的天线阵列跟踪效果最好。无论在σ2=(0.25°)2还是σ2=(0.5°)2情况下，UPA⁃64×64的跟踪性能都最差。这可能是由于尺寸较大的阵列可以产生较窄的波束，对角度的变化较敏感，导致跟踪的精度下降。

3.3 对比EKF算法

将三维UKF跟踪方法和文献［14］的EKF跟踪方法进行对比。实验参数为，收发端天线数Mr=Nr=Mt=Nt=16，SNR为20 d B，仿真5 000次。图7显示了仿真结果，角度变化方差分别为σ2=(0.25°)2和σ2=(0.5°)2。

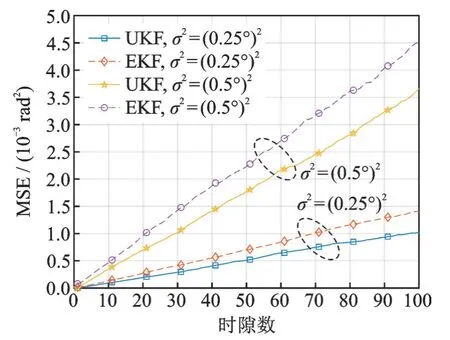
图7 三维UKF与EKF跟踪方法对比Fig.7 Comparison of 3D UKF and EKF track⁃ing methods

如图7所示，随着跟踪时间的增长，两种算法的跟踪误差均增大；随着信道角度方差变化的增大，两种算法的跟踪误差均增大；UKF的跟踪误差小于EKF的跟踪误差，即基于UKF算法的三维跟踪精度优于EKF算法。这是由于EKF在对非线性方程进行泰勒展开时，只保留了一阶项，所以不可避免地会引入较大误差。而UKF不需要进行线性化，没有忽略高阶项，因此能够克服EKF精度不够的问题。

4 结束语

本文在无人机毫米波窄波束通信环境下，采用了一种基于UKF的三维波束跟踪方法。该方法在收发两端均采用均匀平面天线阵，利用无迹变换来解决均值和协方差的非线性传递问题，实现了对俯仰角和方位角的跟踪。仿真结果表明，基于UKF的三维波束跟踪算法性能要优于EKF跟踪算法，UKF可以有效地提高无人机在三维环境下的波束跟踪精度。但本文并未真正涉及无人机动态信道模型，因此，在未来的研究中，将要着重于算法与真实无人机信道模型的结合。