基于三维轴距的水印算法*

唐 晗，陈留洋，鲁荣波

(1.吉首大学信息科学与工程学院,湖南 吉首 416000；2.洛阳师范学院国土与旅游学院,河南 洛阳 471934)

随着网络的发展与计算机的普及，数字作品的储存、复制及传播越来越方便，人们传递和共享信息的方式逐渐从纸质作品向数字作品过渡.数字作品方便携带，还能随时随地传播和编辑，这使得其被盗版的风险增大.研究表明，对数字作品进行数字水印技术处理，可以有效地保护信息安全、降低盗版风险[1].

为了提高数字水印的不可见性和鲁棒性，有学者利用不同的信息特征作为水印信息，还有学者选择不同的水印嵌入位置、不同的水印嵌入因子强度等，并设计了相应的水印算法[2-7].2015年，黄光亚等[8]提出了基于三维轴距的去噪算法，算法的去噪效果很好.由于三维轴距具有计算量小，且轴距越大概率越小的特点，因此笔者拟基于构建三维轴距的方法设计新的水印算法，以期让水印具有较强的不可见性和鲁棒性，解决版权归属不明等问题.

1 预备知识

1.1 三维直方图

三维直方图[9]由邻域均值、图像灰度及邻域中值组成.对于大小为M×N的图像，像素点(i,j)处模板为k×k的邻域均值用g(i,j)表示，像素点(i,j)的灰度用f(i,j)表示，则有[8]

(1)

用h(i,j)表示(i,j)处模板为k×k的邻域中值，

h(i,j)=med{f(i+m,j+n)}.

(2)

其中：m=-(k-1)/2,-(k-1)/2+1，…，(k-1)/2；n=-(k-1)/2,-(k-1)/2+1，…，(k-1)/2；med代表中值运算.根据三维直方图的定义，将f(i,j),g(i,j)和h(i,j)构成的三元组(x,y,z)定义为三维直方图的空间分布，即在三维坐标系中X轴表示灰度f(i,j)，Y轴表示邻域均值g(i,j)，Z轴表示邻域中值h(i,j).

1.2 三维轴距

以8 bit整型数据保存的图像作为研究对象，其灰度分布范围为[0，255]，称由(0,0,0)到(255,255,255)的对角线为图像分布的中轴线[8].像素点f(i,j)的三维轴距是指三维直方图中的点(x,y,z)到中轴线的距离(用d表示)，如图1所示.

图1 三维轴距d

图1中，矢量a表示点(x,y,z)的单位向量，b表示中轴线方向的单位矢量，于是

|a×b|=|a|·|b||sinθ|.

(3)

结合(3)式和图1可得

d=|a|·|sinθ|=|a×b|/|b|.

(4)

2 基于三维轴距的水印嵌入和提取

2.1 水印预处理

为了保证水印信息的安全，在水印嵌入之前通常先对水印图像W(x,y)进行加密.笔者采用计算鬼成像加密技术[10]对原水印图像进行预处理，计算鬼成像加密系统如图2所示.

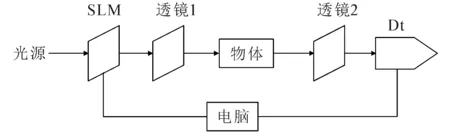
图2 计算鬼成像加密系统

2.2 水印的嵌入过程

利用粒子群优化算法，在载体图像的三维轴距最大点的像素点中寻找最优值作为水印嵌入位置.水印嵌入流程如图3所示.

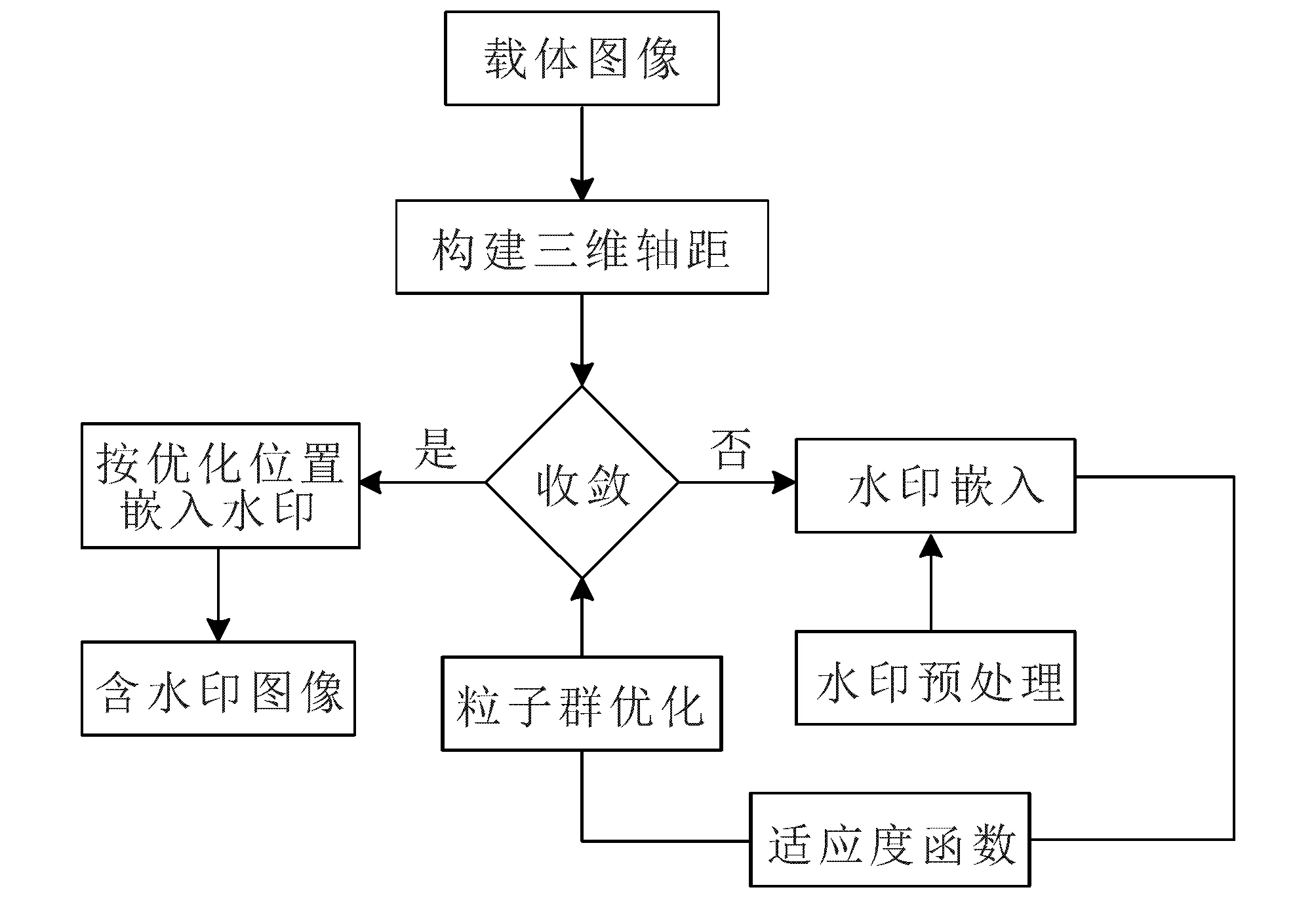
图3 水印嵌入流程

水印嵌入的具体步骤如下：

Step1对原水印图像作预处理.

Step2读入载体图像，利用(1)，(2)式画出三维直角坐标系.

Step3利用(4)式求轴距最大时所有像素点的个数.

Step4以所有像素点个数作为粒子群寻优的初始值.以峰值信噪比(Peak Signal to Noise Ratio，PSNR，用R表示)和归一化相关系数 (Normalized Correlation，NC，用C表示)的线性组合来确定粒子群的适应度函数，适应度函数可以反映水印的鲁棒性和不可见性.PSNR越大，说明水印的不可见性越好；NC越接近1，说明水印的抗攻击性越强.设置适应度函数[12]

f=k1logR+k2C.

其中：k1,k2∈(0,1)，且k1+k2=1，这里取k1=0.3，k2=0.7；

(5)

(6)

Step5将所有像素点的适应度值从大到小排序，选择适应度值最大的点作为水印嵌入的位置.水印嵌入原则是加法准则，将嵌入水印的位置的像素点作为水印提取的密钥.

Step6输出含水印的图像.

2.3 水印的提取过程

水印提取的步骤如下：

Step1读入图像，由密钥找到嵌入水印的位置，利用减法准则提取嵌入的水印图像.

Step2利用计算鬼成像加密系统的相位密钥Pi(x,y)进行计算，完成水印图像重建.

3 仿真实验结果与讨论

3.1 不可见性仿真实验

利用Matlab软件进行不可见性仿真实验.选择规格256×256的2幅图像(图4和图5)作为载体图像，32×32的二值图(图6)作为水印图像.通过计算可得，载体图像(图4)与嵌入水印图像(图7)的PSNR为40.922 8 dB，提取出的水印图像(图8)与原始水印图像(图6)的NC达到0.998 3；载体图像(图5)与嵌入水印图像(图9)的PSNR为39.744 8 dB，提取出的水印图像(图10)与原始水印图像(图6)的NC为0.983 3.由此可知，基于三维轴距的水印算法下的水印具有良好的不可见性.

图4 “小女孩”原载体图像

图5 “Lena”原载体图像

图6 嵌入载体图像中的原始水印图像

图7 “小女孩”含水印图像

图8 从“小女孩”提出的水印图像

图9 “Lena”含水印图像

图10 从“Lena”提出的水印图像

3.2 鲁棒性仿真实验

利用Matlab软件做多种攻击的仿真实验.选择规格256×256的“Lena”图像作为载体图像，32×32的“王”字图像作为水印图像.令JPEG压缩因子为50，均值滤波窗口大小为5×5，中值滤波为2×2，对比度增强30%，几何剪切为1/4，等比放大倍数为1.3，旋转15°.为了验证算法的鲁棒性，将受各种攻击的本研究的NC测试结果与文献[13-15]中的进行对比(表1).

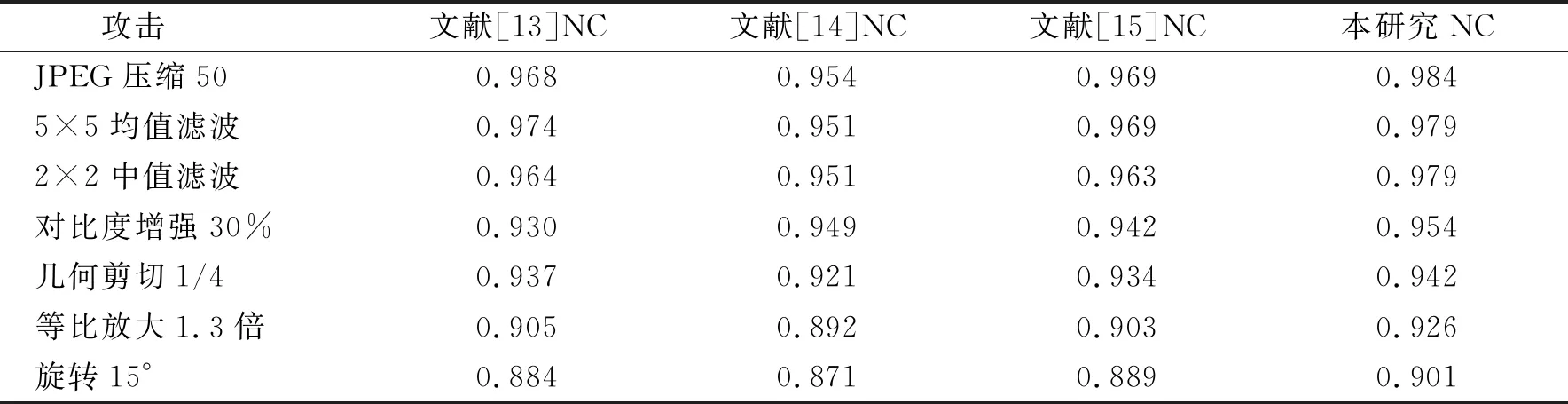
表1 NC测试结果对比

由表1可知，各种攻击下的本研究的NC结果都优于文献[13-15]，说明基于三维轴距的水印算法下的水印的抗攻击性最强.

4 结语

为了提高水印的不可见性和鲁棒性，提出了基于三维轴距的水印算法.首先利用计算鬼成像加密技术对原水印进行预处理，提高水印的安全性；然后通过构建三维轴距的方法，计算得到轴距最大时的所有像素点；最后利用粒子群优化算法在这些像素点中找到最优值作为水印的嵌入位置，完成水印的嵌入.由仿真实验结果可知，在多种攻击下(如JPEG压缩、对比度增强、滤波、旋转及放缩等)，基于三维轴距的水印算法能使水印具有良好的不可见性和优越的鲁棒性.