电力系统分裂法潮流及其应用研究

矫 贺，李宝国

电力系统分裂法潮流及其应用研究

矫 贺，李宝国

（辽宁工业大学 电气工程学院，辽宁 锦州 121001）

针对目前规模庞大的现代电力网络，采用分裂法是提高大电网潮流解算效率的有效方法之一。首先对新能源发电节点进行分析并按不同控制手段下的节点类型分类，建立含新能源的现代电力系统综合数学模型。然后在基本分裂法基础上对分裂法进行改进，给出了基于广义Tellegen定理的电流注入型LU分解分裂法潮流，对分裂节点、协调变量以及各子块内的不同类型节点进行处理，与广义Tellegen定理相结合，从而提高分裂法潮流计算速度，增强了应用分裂法潮流计算的适应性。通过算例仿真分析，验证了改进分裂法的可行性。

分裂法潮流；LU分解；广义Tellegen定理；现代电力系统；节点处理

随着电力系统网络规模不断扩大，潮流计算出现了计算量过大及难于收敛等问题。为解决此问题，将一个复杂的系统模块分成多个简单的子模块，然后将每个子模块分配给多个计算节点进行分别求解，由此开发了并行算法[1-3]。分裂法起源于大网络的划分理论，基本思路是“化整为零”，将一个完整大型网络划分为几个较小的部分，通过每一个小部分的求解，得到整体网络的解。分裂潮流算法包括切割支路电流法、分裂节点电位法、切割回路电流电压法等基本方法。1992年，Torralba等[4]提出电力系统潮流的分块并行算法，其实现是从线性方程组的因子分解和前推回代完成。文献[5]结合电力系统网络具有很强的稀疏性，以分割理论下的对角块加边网络模型(BBDF)为基础提出异步块牛顿迭代法，有很好的收敛性。文献[6-7]基于支路切割的网络分块方法的基础上提出了切割回路电流法的网络分裂计算。文献[8]采用网络分块以切割支路的方式，处理带有虚拟负荷形式的协调变量，有效地将大规模电力系统的潮流计算问题转化为若干个子网络的潮流计算问题。文献[9]介绍的二级多重分裂迭代法是一类新的求解大规模稀疏线性代数方程组的有效并行计算方法，并结合配电网潮流计算，从数学和物理意义上对内外分裂方法进行描述，继而导出基于二级分裂迭代法的配电网潮流计算方法。

1 模型建立

1.1 节点分类

在潮流计算时需对PQ节点进行相应处理，当风力发电采用同步发电机进行并网连接时，将该节点看作PQ节点[10]。对于通过电流控制的逆变器与电网进行相连接情况下的节点进行PI节点处理[11]。将燃料电池和并网电压控制的光伏发电源看作PV节点。然而，在实际运行中，对于节点类型是PV节点的分布式发电电源存在无功功率的限度范围，需要将PV节点转变成PQ节点进行计算。当选择异步发电机与电网连接时，节点类型看作P-Q(V)节点。

1.2 综合模型建立

含新能源的电力网络综合模型示意图如图1所示。

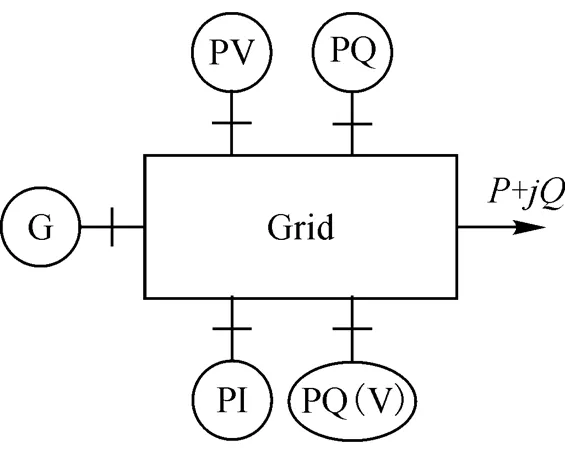
图1 综合模型示意图

对于个节点的电力网络，若节点注入功率及参数给定，可以得到直角坐标系下的电力网络方程：

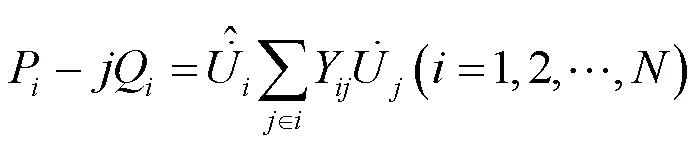
2 改进分裂法

结合节点分裂法和支路切割法的分裂原理，将两类型网络方程合并，可以得到统一的网络分裂法方程，在利用该分裂方法对系统进行分裂时，需要选择分裂节点与切割支路[12]。

对节点导纳方程进行改写，若考虑电流注入，则电流注入模型简写为：

表示的是导纳矩阵；表示对角块阵；Δ表示节点电压变化量；Δ表示节点注入电流变化量。系统被分裂之后形成的各近似且独立的子模块，数量是-1个，此外还存在公共的部分，这类子模块数量为个，式(3)可以表示为如下形式：

带有“·”的元素表示经过电流注入模型变换之后的元素，对矩阵内元素进行分裂操作，使阶数减少，操作后的方程组表达式如下：

对于分裂后的第个子模块，假设内部共有个节点，第个节点为平衡节点，个PQ节点，-个PV节点，-个PI节点，其余为P-Q(V）节点；对于处于边界位置的协调系统，共有个节点，个PQ节点，-个PV节点，-个PI节点，其余为P-Q(V)节点。

(7)

(8)

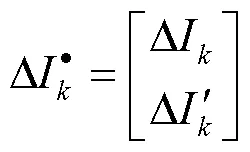
(10)

(11)

对于各个子模块内的PQ节点：

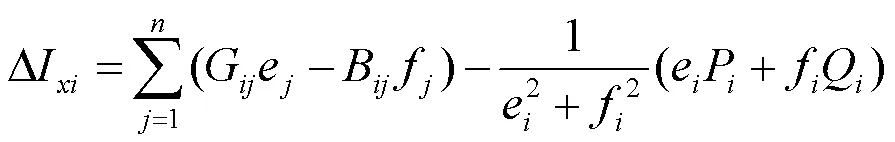
对于各个子模块内的PV节点，因为此类节点的特点是节点的电压和有功功率是作为已知的前提条件，因此可以求出无功功率值，计算公式如式(14)所示：

对于各个子模块内的PI节点，因为此类节点是节点电流和有功功率作为前提条件给出，通过计算可以得到无功功率值，计算式见式(17)：

(17)

以此作为已知量，并在每次迭代过程中不断更新，其中：

在协调块内，对于PQ节点：

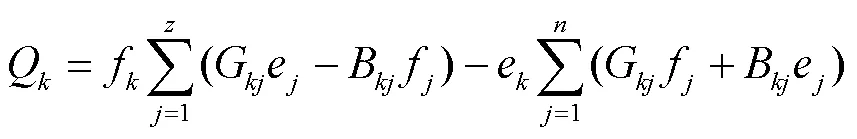
(27)

以此作为已知量，并在每次迭代过程中不断更新，其中：

在协调块内，对于PQ(V)节点，注入电流不平衡量表达式见式(30)、式(31)：

对式(5)进行公式展开，得到关于分裂后单独子模块内的节点电压的修正量Δu和处于分裂边界处的协调模块内节点电压的修正量Δu的方程，见式(32)～式(35)：

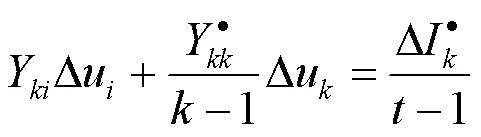
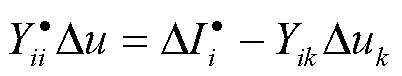
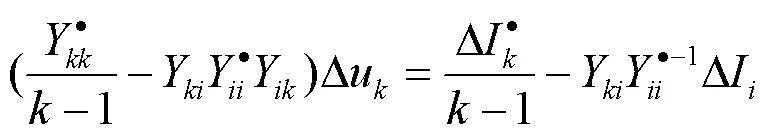
计算求解分裂边界处的协调子模块时，要确保对角块和协调子模块一致，若两类子块不一致，则不能利用每个对角块来对另一个子块进行求解，将产生与实际情况相差很大的结果，因此，形成如式(36)所示方程并求解：

在对角块和协调子模块拥有一致性的情况下，首先进行第一次计算，求出解x。第二次计算将所求得的解x代入每个对角块内，然后计算出每个对角块的解x。

为提高解算速度，本文对经过重组的节点导纳矩阵，采用LU分解法分解为：

方程组的求解过程可用式(38)与式(39)描述：

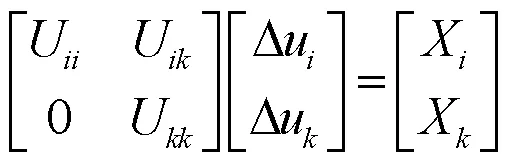
将式(38)与式(39)展开，得到式(40)与式(41)：

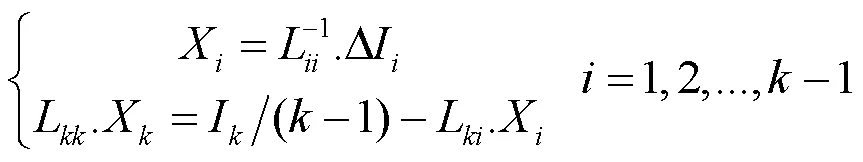
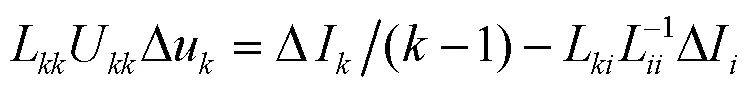
至此，完成了LU分解法的前代操作，再由回代操作计算出对角块的解Δu：

利用广义Tellegen定理的差形式，对电流注入型的LU分解分裂法进行优化修正：

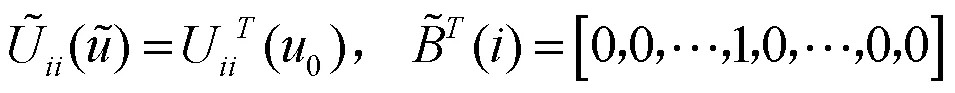
则根据小扰动定理，有：

3 计算流程

(1)给定系统各节点的电压初始值。

(3)计算节点电流以及节点电压值。

(4)计算系数矩阵，并进行LU分解。

(5)计算子块中各自的节点电压并进行修正。

(6)在协调块中，求出电压修正量并进行修正。

(7)将协调块电压代入各子块中，计算出电压修正量。

(8)对子网内的各节点的电压向量进行修正。

(9)计算PV节点的无功功率。

(10)将电压值代入功率方程进行迭代。

(11)子块内检验是否收敛，若收敛，发送标志给协调块；若不收敛，子块内继续迭代，到迭代次数限制，无论收敛与否，发送不同标志给协调块。

(12)协调块收到各子块收敛标志，若各子块均收敛，则潮流收敛，输出计算结果。否则继续解方程求出电压的修正量，并进行修正。

(13)求雅克比矩阵中各元素的值。

(14)在子块中，求得注入电流的变化量。

(15)计算电压变化量。

(16)返回(8)继续迭代。

4 仿真验证

在IEEE30节点系统算例仿真中，选择了光伏发电、风力发电、燃料电池等新能源发电类型。光伏源发电并入系统内的第3节点，节点类型为PI节点；燃料电池并入系统内的第16节点，节点类型为PV节点；同步发电机型风力发电并入系统内的第21节点，节点类型为PQ节点；异步电机型风力发电并入系统内的第26节点，节点类型为P-Q(V)节点。节点采用改进的分裂法潮流进行计算时，结合接入新的发电类型，对系统进行分裂。为了更方便计算，在分裂时考虑区域性以及各模块之间的通信联系，因此选择第6、10、12、20号节点作为分裂节点，选择第23、24支路作为切断支路。

对比并入新能源发电节点之后，分别采用传统分裂法潮流算法和改进分裂法潮流算法进行计算，2种潮流计算结果对比如表1所示。

表1 潮流计算结果比较

测试系统传统分裂法改进分裂法 30节点0.032 s(6次)0.028 s(5次)

由表1的结果数据可见，在相同的收敛精度下，本文法与传统法计算结果相近，但迭代次数比传统分裂法迭代次数少，具有更快的计算速度。

5 结语

给出了一种基于广义Tellegen定理的电流注入型LU分解的分裂潮流计算方法，该方法在基本的分裂法算法上进行改进，减少了迭代次数，并且提高了潮流计算速度，增强了应用分裂法潮流计算的适应性。通过算例仿真分析，验证了改进分裂法的可行性。

[1] 李亚楼, 周孝信, 吴中习. 基于PC机群的电力系统机电暂态仿真并行算法[J]. 电网技术, 2003, 27(11): 6-12.

[2]Torralba A. Three methods for the parallel solution of a large, sparse system of linear equations by multiprocessors [J]. International Journal of Energy Systems, 1992, 12(1): 1-5.

[3]Decker I C, Falcao D M. Conjugate gradient methods for power system dynamic simulation on parallel computers[J]. IEEE Transactions on Power Systems, 1996, 11(3): 1218-1227.

[4]Torralba A, Gomez A. Three methods for the parallel solution of a large sparse system of linear equations by multiprocessors[J]. Int J Energy Systems, 1992, 12(1): 1-5.

[5]苏新民, 毛承雄, 路继明. 对角块加边模型的并行潮流计算[J]. 电网技术, 2002, 26(1): 22-25.

[6]郭志忠, 刘海滨, 柳焯. 切割回路电流法的网络分裂计算[J]. 哈尔滨工业大学学报, 1994, 26(5): 88-92.

[7] 郭志忠. 电力网络解析论[M]. 北京: 科学出版社, 2008.

[8]万黎, 陈允平, 徐箭. 基于节点迁移的电力系统并行计算优化分割策略[J]. 电网技术, 2007, 31(11): 42-48.

[9]汪芳宗, 向小民, 胡翔勇. 基于二级分裂迭代法的配电网潮流计算方法[J]. 电力系统自动化, 2007(15): 41-45.

[10]唐小波, 徐青山, 唐国庆. 含分布式电源的配网潮流算法[J]. 电力自动化设备, 2010, 30(5): 3437.

[11] 王守相, 黄丽娟, 王成山, 李东. 分布式发电系统的不平衡三相潮流计算[J]. 电力自动化设备, 2007, 27(8): 11-15.

[12] 张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 北京: 清华大学出版社, 2007.

Research on Diakoptics of Power Flow and Its Application in Power System

JIAO He, LI Bao-guo

（School of Electrical Engineering, Liaoning University of Technology, Jinzhou 121001, China）

In view of the large-scale modern power network, the diakoptics is one of the effective methods to improve the efficiency of large-scale power flow calculation. First, the new energy power generation nodes are analyzed and classified according to the node types in different control methods, and a comprehensive mathematical model of the modern power system with new energy is established. Then on the basis of the basic diakoptics, the diakoptics is improved, and the current injection type LU decomposition diakoptics power flow based on the generalized Tellegen theorem is given. The split nodes, coordination variables and different types of nodes in each sub-block are processed, and the generalized combination of Tellegen’s theorem helps to increase the speed of power flow calculation of the diakoptics, which enhances the adaptability of the application of diakoptics for power flow calculation. The simulation analysis of a numerical example verifies the feasibility of the improved diakoptics.

diakoptics power flow; LU decomposition; generalized Tellegen theorem; modern power system; node processing

10.15916/j.issn1674-3261.2021.06.007

TM615

A

1674-3261(2021)06-0383-05

2021-07-17

矫 贺(1996-)，女，辽宁铁岭人，硕士生。

李宝国(1966-)，男，辽宁义县人，教授，硕士。

责任编辑：孙 林