基于试验对比的汽车轮毂动特性及疲劳寿命研究

唐贵基，喻自力，王晓龙，白 洁，高会超

基于试验对比的汽车轮毂动特性及疲劳寿命研究

唐贵基1，喻自力1，王晓龙1，白 洁1，高会超2

（1. 华北电力大学 机械工程系，河北 保定 071000；2. 保定市立中车轮制造有限公司，河北 保定 071000）

为研究汽车轮毂承担动态载荷下的性能，以铝合金轮毂为研究对象，基于有限元建模仿真的方法对轮毂结构的固有频率及振型等固有特性进行分析，并通过现场模态试验测试对有限元分析结果进行了验证。此外，对轮毂做进一步静力学仿真分析，在获取轮毂受载状态下应力云图基础上，分析了轮毂的疲劳寿命及最易失效部位，并通过轮毂全寿命周期加速疲劳试验对仿真分析结果进行验证。通过有限元仿真分析结果与实际试验结果的对比，验证了所述建模仿真方法的准确性及可靠性，为研究轮毂固有特性、提高疲劳寿命及结构优化设计提供理论依据。

轮毂；固有特性；模态试验；疲劳寿命分析；疲劳试验

轮毂作为汽车的重要安全部件，行驶时承受各种交变载荷，因此要求轮毂具有良好的动特性与足够的疲劳寿命。随着有限元计算与试验设备、技术的不断发展，可以更好地研究结构动态性能，为结构优化提供依据。文献[1]基于ANSYS建立参数化有限元模型，再通过试验模态进行验证，在确定模型的可靠性基础上逐渐优化实体结构模型。文献[2]基于有限元方法模拟物体被接触挤压中的内部受力，从而分析内部结构损伤规律，为结构设计与控制方法提供数据参考。文献[3]基于ANSYS对结构进行模态分析与预测，理论分析上提高动态性能，模型修改前后结构动特性与模态特性发生变化。文献[4]基于有限元理论计算某圆管结构承受动态轴向载荷下的冲击能量，修改的模型在实际试验中较之前的结构在能量吸收特性方面有明显的优化。文献[5]通过处理实验平台下的加速度信号，将试验获取结构的前四阶固有频率与振动模式与数值计算相验证。文献[6]通过有限元数值计算方法对于集成动力学模型的动态特性建立评估函数，并基于评估函数简化结构的等效模型。文献[7]将有限元分析引入传统轮毂设计流程，增强产品造型创新与设计效率。为优化轮毂结构设计，分析轮毂结构动特性与疲劳寿命性能，本文通过有限元仿真与试验结合对比分析，获得轮毂的动特性，验证仿真分析的可行性；并依据疲劳寿命曲线进行疲劳寿命分析，再通过弯曲疲劳试验发现疲劳裂纹处与仿真分析一致，验证了该方法的准确性，为结构优化提供理论与试验依据。

1 有限元模型

1.1 计算原理

有限元方法基本思想将结构进行离散，将载荷离散分布到各节点，分别计算节点位移与应力分布。为分析单元应力特性，利用多种方程求解应力与应变关系，通过几何方程建立单元体应变矩阵：

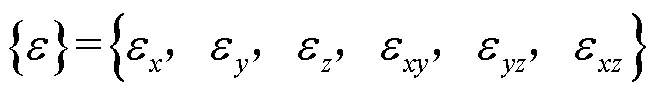
为分析结构内的小变形与线性弹性，获得其单元体内的应力矩阵，根据物理方程进行变换：

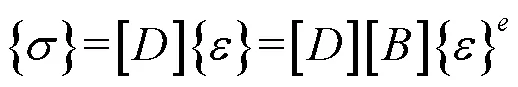
式中：[]为几何矩阵，[]为弹性矩阵。

通过虚功原理得出各单元体中的力：

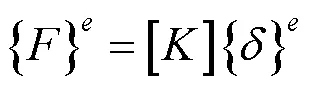
式中：[]为整体刚度矩阵。

对于整体结构上的任意一点，建立平衡方程：

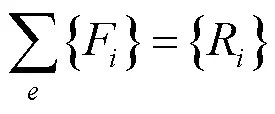
式中：{R}为节点上的外载荷。

结合单元体受力情况与边界条件，得出所结构体的整体平衡方程：

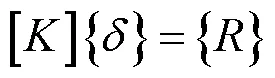
式中：[]为整体刚度矩阵，{}为整体结构节点位移矩阵，由式(1)、式(2)求出各单元的应变和应力，式(5)求出节点位移。

1.2 模型建立

考虑轮毂的强度、质量以及散热等性能，轮毂模型材质为铝合金A356，参数如表1所示。

表1 轮毂材料参数

材料类型弹性模量/MPa泊松比密度/(kg·m-3) 铝合金710000.332770

由于轮毂模型中有螺栓孔、气门孔以及连接中心孔，因此通过Space Claim对于模型中的线以及圆面进行合并以及删除处理，所建立的有限元模型如图1所示。

图1 汽车轮毂模型

1.3 网格划分与约束施加

基于有限元思想进行网格划分以及模态分析，由于有限元模型网格质量关系着是否能够得到高精度、高吻合的分析结果[8]，因此，对轮毂进行网格划分时，全局网格控制规则采取Curvature，对于螺栓孔、中心孔附近曲率变化处网格自动加密[9]，通过ANSYS workbench对模型进行前处理，模型采用四面体单元，获得网格如图2所示。

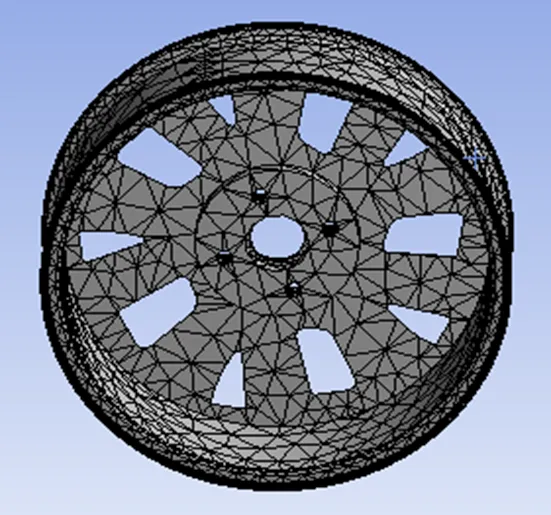
图2 网格划分

模型包括69 726个节点，37 238个单元。考虑到轮毂实际使用中与汽车车轴通过螺栓紧固连接，因此，对4个螺栓孔施加全约束进行模态分析。

2 固有特性分析

2.1 模态分析

模态分析是一种确定结构振动特性的技术，是结构运动学的基础[10]。结构设计过程中，利用有限元仿真进行模态计算，并据此进行优化设计[11]。经过有限元分析获得固有频率、模态振型等，来解决复杂的结构振动问题、振动测量与结构的动力学分析，表2为通过有限元仿真分析获得的动特性参数，对应的四阶模态振型如图3所示。

表2 模态分析结果

阶数模态频率/Hz模态振型 1365.09轮辋弯曲 2787.4轮辋偏转 31276.9三角形振动 41834.8四边形弯曲

图3 四阶振型图

固有特性分析结果通常可用于结构优化中的数据指导，来尽量避免结构出现共振导致功能失效。考虑汽车实际行驶中的路况，城市路况较好，平坦路面激励频率或者石子路等激励频率一般低于15 Hz，发动机的转速对应频率如公式(6)所示。

式中：为内燃机转速，r/min；为气缸数目；为冲程数目，四行程2，两行程1。

一般发动机转速可达8 000r/min，则0=267 Hz，汽车行业中的共振带范围一般取固有频率的13%到20%的范围，当激励频率和结构固有频率满足式(7)时，会发生共振。

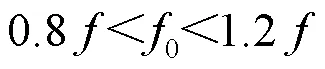
式中：为固有频率；0为激励频率。

轮毂一阶固有频率为365.09 Hz，若按照20%的频率范围，共振带范围为292～438 Hz，当四缸发动机加速到最高转速，对应的激励频率仅为0=267 Hz，未达到轮毂的共振频带覆盖范围内，因此正常行驶状态下轮毂不会出现共振现象，能够保障车辆行驶的安全性。为验证所构建轮毂有限元模型分析结果的准确性，进行轮毂模态测试试验，用于对比有限元分析结果及现场试验测试结果。

2.2 模态试验验证

模态试验采用北京东方振动和噪声研究所的成套设备对于轮毂进行分析，配套设备的具体型号如表3所示.

表3 试验仪器设备

设备名称型号 北京东方所数据采集系统INV3018A 模态试验分析系统DASP-V10 加速度传感器INV9824 模态力锤INV9310

现场模态试验设备如图4所示，图4中(a)为模态力锤，(b)为加速度传感器，(c)为试验轮毂，使用DASP-V10系统进行加速度数据的分析处理。

图4 模态试验设备

试验中采用螺栓孔螺栓固定约束，对于四个螺栓孔施加120 N·m的扭矩进行固定；激励方式为力锤激励法，试验共进行20次激励，激励点分布在传感器附近的2点以及对称的2点，以及轮毂背面与正面激励点平行的4点；2传感器安装位置呈90°分布，在传感器底座上涂抹热熔胶，如图(b)所示垂直安装在轮缘上；在INV3018A采集系统中设置采样频率为20 kHz，激励时轮毂正面4个激励点各激励3次，背面4个激励点各激励2次，为保证加速度传感器的数据的准确性，每次使用力锤快速敲击激励点并采样，等采集系统中的数据波形完全振荡衰减后再进行下1次激励。

为避免每次激励力度不同可能对加速度传感器中数据带来的影响，在计算频响函数时，加窗函数对采集到的波形进行截断处理，通过模态试验分析系统对20次加速度数据进行加窗函数，并处理拟合得到如图5所示频响函数曲线图。

图5 频响函数曲线

对图5中的频响函数图进行标定得出如表4所示轮毂前四阶固有频率，将之与仿真分析所得固有频率进行对比，计算误差。

表4 有限元分析与试验结果对比

实测频率/Hz分析频率/Hz误差/% 357.8365.092.0 813.4787.43.2 1358.11276.95.9 1980.91834.87.3

通过表4中有限元仿真分析与模态试验结果对比发现，试验分析中的频响函数曲线可以明显地得到轮毂的四阶固有频率，但是仿真分析中含有多阶频率，存在同阶不同方向上的振型，且模态试验中传感器会受环境影响，但两者结果对比得出误差较小，说明仿真模型与实际模型误差在允许范围内。

3 静力学分析

3.1 载荷分析

通过仿真分析与模态试验的结果对比验证了有限元模型的可靠性，再对承载实际载荷下的汽车轮毂进行静力学分析，分析其动态特性。车辆行驶时力与力矩通过轮胎传递到轮辋，在倾斜路面行驶转向时，车轴还将承受弯矩，因此依据动态弯曲疲劳试验进行载荷的计算与施加。

根据文献[12]，轮毂所受最大载荷可按照公式(8)确定。

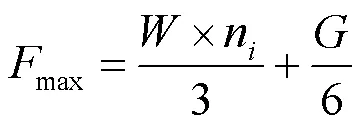
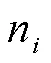
轮毂在汽车行驶中，支撑汽车载重的同时，承受弯曲载荷，根据GB/T 5334-2005《轿车钢制车轮性能要求和试验方法》中动态弯曲疲劳试验要求，弯矩按照公式(9)计算。

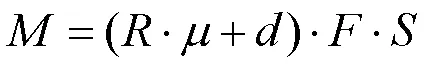
经计算，=3 046 N·m。

3.2 应力分布

基于如上计算得出轮毂所承受的载荷，再进行载荷施加及仿真动力学分析得到如图6所示等效应力图，分析图6可以得出应力主要集中在轮辐与窗口上，其中最大等效应力为117.65 MPa，分布在轮辐中间的窗口处，窗口附近的轮辐部位承受应力也达到了104.58 MPa，由于铝合金A356的屈服强度值为240 MPa，因此，应力最大处有较高的安全系数和较高的强度储备。

图6 等效应力图

3.3 疲劳寿命分析

承受长期交变载荷后，应力最大处可能最先出现疲劳失效，因此需进行疲劳寿命分析。金属构件的寿命预测方法主要有基于应力的寿命预测方法和基于应变的寿命预测方法[13]。应力疲劳寿命预测中，基于S-N曲线进行预测，工程中用Basquin方程表示横幅载荷下疲劳寿命应力的关系[14]，如式(10)所示。

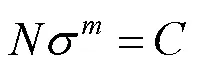
零件或材料的疲劳曲线是零件疲劳寿命预测的基础，材料曲线一般通过试验得到，也可以通过估算绘制出简单的曲线[15]，基于铝合金A365的一些试验参数绘制如图7所示的疲劳寿命曲线。

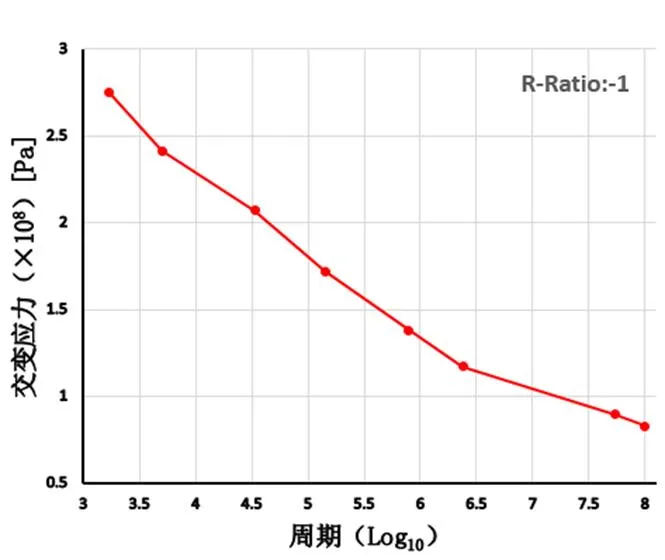
图7 材料疲劳寿命曲线

通过Fatigue Tool对轮毂进行疲劳寿命分析[16]，得到图8所示疲劳寿命云图，轮毂疲劳寿命最小值出现在轮辐窗口处，最小疲劳寿命能承受2.343×106次周期的循环载荷。国家GB/T 5334—2005《乘用车车轮性能要求和试验方法》中疲劳试验要求轻合金车轮最低循环次数为5×105次，因此符合国家标准。

图8 疲劳寿命分析

3.4 疲劳试验验证

通过分析疲劳寿命云图得出疲劳寿命最低处，为验证其分析结果，使用CFT-3轿车车轮弯曲疲劳试验机对轮毂进行弯曲疲劳试验，设备如图9所示。

试验中法兰盘为4孔均匀分布法兰盘，孔内径

图9 疲劳试验台

为100 mm，使用120 N·m的扭矩将4个螺栓进行紧固，而后通过8个压板将轮毂的下边缘固定，试验机所给弯矩为3 046 N·m，设置自动停机的主轴偏移量为初始的10%，主轴转动直至主轴偏移量达到设定偏移比，得到如图10所示疲劳失效裂纹。由于轮辐窗口属于应力最集中处，在承受交变载荷后最先出现疲劳失效，图10试验结果与仿真分析结果一致，通过有限元仿真分析结果与实际试验结果的对比，验证了所述建模仿真方法的准确性，为研究同类汽车轮毂的固有特性及结构优化设计提供理论依据与技术支持。

图10 疲劳失效部位

4 结论

本文基于有限元仿真进行汽车轮毂的动特性及疲劳寿命分析，并进行模态试验以及疲劳试验得到轮毂的应力最大以及疲劳寿命最小处对仿真结果进行验证。为研究轮毂固有特性、提高强度及结构优化设计提供理论依据。

(1)通过模态试验的频响函数曲线，计算轮毂一阶固有频率与仿真分析结果误差较小，都避开一阶共振频率，不会产生共振。

(2)进行静力学分析，应力集中在轮辐窗口处，应力最高为117.65 MPa，该应力小于材料的屈服强度240 MPa，具有较高的安全系数与强度储备。

(3)绘制疲劳寿命曲线，进行疲劳寿命分析，得出轮毂疲劳寿命最小值在轮辐窗口处，最小疲劳寿命能承受2.343×106次周期的循环载荷，完全满足国家标准，失效部位与疲劳试验相符合。

(4)将有限元分析与相关试验对比分析，并依据疲劳寿命曲线进行分析与弯曲疲劳试验验证疲劳薄弱处，为结构优化提供理论基础与依据。

[1] 邱白晶, 何耀杰, 盛云辉, 等.喷雾机喷杆有限元模态分析与结构优化[J]. 农业机械学报, 2014, 45(8): 112-116, 105.

[2] 姬伟, 李俊乐, 杨俊, 等. 机器手采摘苹果抓取损伤机理有限元分析及验证[J]. 农业工程学报, 2015, 31(5): 17-22.

[3] 李天箭, 吴晨帆, 沈磊, 等. 基于模态预测及敏度分析的机床动特性设计方法[J]. 机械工程学报, 2019, 55(7): 178-186.

[4] Ahmad M, Ismail K A, Hanid M H M, et al. Modification of the design of circular thin-walled tubes to enhance dynamic energy absorption characteristics: Experimental and finite element analysis[J]. IOP Conference Series: Materials Science and Engineering, 2020, 917(1): 1-13.

[5] Fan W, Yang Y, Su X. Dynamic Modeling and Vibration Characteristics Analysis of Transmission Process for Dual-Motor Coupling Drive System[J]. Symmetry, 2020, 12(7): 1171-1190.

[6] Xu M T, Cai B, Li C Y, et al. Dynamic characteristics and reliability analysis of ball screw feed system on a lathe[J]. Mechanism and Machine Theory, 2020, 150:1-21.

[7] 闫胜昝, 刘伟鹏. 基于有限元分析的铝合金轮毂造型设计[J]. 机械设计, 2014, 31(10):109-112.

[8] 张颖, 王元清, 张俊光, 等. 铝合金网壳结构箱型-工字型盘式节点单肢受力性能有限元分析[J]. 工程力学, 2020, 37(S1): 130-138.

[9] 李海峰, 吴冀川, 刘建波, 等. 有限元网格剖分与网格质量判定指标[J]. 中国机械工程, 2012, 23(3): 368-377.

[10] 代颖, 崔淑梅, 宋立伟. 车用电机的有限元模态分析[J]. 中国电机工程学报, 2011,31(9): 100-104.

[11] 马骊凕, 朱智民, 安占飞, 等. 轿车白车身模态分析[J]. 振动与冲击, 2013, 32(21): 214-218.

[12] 王明明. 铝合金汽车轮毂结构设计及优化[D]. 长春: 吉林大学, 2011.

[13] 朱峰, 杨宏伟, 王本劲, 等. 航空导管弯曲试验的疲劳裂纹萌生寿命[J]. 力学季刊, 2020, 41(3): 519-527.

[14] 左芳君. 机械结构的疲劳寿命预测与可靠性方法研究[D]. 成都: 电子科技大学, 2016.

[15] 黄宁. 大型结构件的疲劳寿命预测方法研究[D]. 长沙: 中南大学, 2013.

[16] 沈明明, 李荣, 刘祖国, 等. 数控机床轴承结构振动谐响应及疲劳寿命研究[J]. 组合机床与自动化加工技术, 2019(11): 143-147.

Research On Dynamic Characteristics and Fatigue Life of Automobile Wheel Hub Based On Test Comparison

TANG Gui-ji1, YU Zi-li1, WANG Xiao-long1, BAI Jie1, GAO Hui-chao2

（1. Department of Mechanical Engineering, North China Electric Power University, Baoding 071000, China; 2. Baoding Lizhong Wheel Manufacturing Co., Ltd., Baoding, 071000, China）

In order to study the performance of automobile wheel hub under dynamic load, aluminum alloy wheel hub taken as the research object, the natural frequency and vibration mode of wheel hub structure were analyzed based on the method of finite element modeling and simulation. The results of finite element analysis were verified by field modal test. In addition, a further static simulation analysis was performed on the hub, and on the basis of obtaining the stress cloud diagram of the hub under load, the fatigue life and the most prone failure position of the hub were analyzed. The simulation results were verified by accelerated fatigue test of the hub life cycle. The accuracy and reliability of the modeling and simulation method are verified by comparing the finite element simulation results with the actual test results, which provides a theoretical basis for studying the inherent characteristics of the hub, the fatigue life and structural optimization design improved.

Wheel hub; inherent characteristics; modal test; fatigue life analysis; fatigue test

10.15916/j.issn1674-3261.2021.06.001

TH133

A

1674-3261(2021)06-0351-06

2021-02-03

国家自然科学基金项目(52005180)；河北省自然科学基金项目(E2019502047)；中央高校基本科研业务费专项资金项目(2021MS069)

唐贵基(1962-)，男，山东龙口人，教授，博士，博士生导师。

王晓龙(1989-)，男，黑龙江大庆人，副教授，博士。

责任编辑：陈 明