轴向压缩载荷下的音板木材振动和声学响应特性研究

翟学勇，苗媛媛，王秀雅，万 珂，尹玉雪，刘镇波

(1.东北林业大学 生物质材料科学与技术教育部重点实验室，哈尔滨 150040；2.东北林业大学 木质新型材料教育部工程研究中心，哈尔滨 150040)

作为音源的音板对乐器发声具有至关重要的作用，在制作音板时，对木材取材部位、纹理方向及含水率等有严格的要求，以保证其优良的声学性能[1-2]，在树种上，传统民族乐器和钢琴等音板一般选择泡桐、鱼鳞云杉等树种木材。为评价木材振动和声学性能的优劣，学者们引入振动声学参数，如比动弹性模量、声阻抗等。音板在装配中会被施加约束，同时会被施加轴压缩载荷[3]，轴向压缩载荷使音板产生预应力以及微观构造的改变，从而对其声学特性产生影响，因此研究轴压载荷对音板木材的振动和声学特性的影响是非常必要的。

以往学者们进行木材声学特性研究时，大多基于梁的振动法，将材料置于自由状态下，利用弹性材料支撑节点位置或利用弹力绳吊装材料，测定其振动频谱，并计算得出其振动声学特性参数[4-7]。虽然这种方法可以较为快速、方便地测定不同尺寸音板木材在自由状态下的声学特性，但忽略了音板木材在乐器中受到复杂应力这一情况。众所周知，在轴向力作用下木材的微观结构会发生变化[8-9]，所以基于自由边界条件下测定音板木材的振动和声学特性并不能完全反映音板木材在乐器产品中的实际状态。

在国内外，不论是新型材料还是传统材料，对其振动和声学性能的研究依然受到学者们的关注，而评价其声学性能时，均是使木材处于自由状态的条件下进行测定[10-15]。Yang等[16]采用自由振动的方法，对琵琶音板材料进行振动和声学测试，利用测定的琵琶音板比动弹弹性模量、声辐射、声阻抗等声学参数，建立了琵琶音板音质预测的多选择模型，通过实际检验模型精度为87.78%；2018年林斌等研究了桦木单板/玻璃纤维复合音板的声学特性，结果表明铺放两层玻璃纤维布的复合材料的振动声学性能最好，并且其比动弹性模量和西加云杉的相接近，说明桦木单板/玻璃纤维复合材料具有替代传统木质音板用材的可能性[17]。但这些研究很少从微观角度深入分析材料的振动声学机理。木材是一种复合材料，主要由木质素，纤维素，半纤维素三大组分组成，这些成分的体积和化学成分的变化，以及孔隙度的数量和分布的差异，决定了木材的结构，进而决定了木材的密度和机械性能[18]。音板木材振动和声学性能的变化必定伴随结构或者化学组分的改变，因此研究轴向压缩载荷作用下的音板木材的微观结构，从微观角度阐述其发声机理具有重要意义。

近年来，材料在使用过程中的结构行为越来越多的受到学者们的青睐。Rajesh等[19]研究了轴向压缩载荷对天然纤维织物聚合物组合梁弯曲和自由振动特性的影响，结果表明，轴压载荷越大，组合梁的自由振动频率越低，模态阻尼系数越高；Waddar等[20]研究了剑麻布/环氧复合材料芯材夹层梁在压缩载荷作用下的弯曲和振动行为，利用万能力学试验机对其施加载荷，采用模态分析装置对载荷下试件的振动行为进行分析，结果同样表明压缩载荷越大，振动频率越低，同时发现基频在试件失稳后会出现指数增长的现象；Corradi等对钢琴音板在生产过程中3个不同阶段的声学行为进行了研究，分别对其进行了模态分析以及数值模拟，并对低频范围的模态振型进行对比，结果发现在相同边界下，琴桥的存在对音板振型影响较小，而不同的边界条件对音板的刚度影响更加突出。

本文以泡桐和云杉为研究对象，对试材施加实际装配中类似的约束以及轴向压缩载荷，研究轴向压缩载荷对音板木材的振动和声学响应特性的影响，并从微观角度初步探索影响音板木材声学性能的因素，为完善音板的评价体系以及寻找实木音板的替代材料提供理论依据。

1 材料与振动试验

1.1 材料

本试验材料由企业提供，其树种分别为产自河南兰考的泡桐，产自东北地区的鱼鳞云杉。所选素板均为径切板，表面纹理通直无结疤，从两种素板中截取尺寸(L×R×T)为300 mm×30 mm×10 mm的18块试材，试件纹理平行于L方向。利用恒温恒湿箱，将试材置于温度为20 ℃、湿度为60%的环境下平衡一个月，使试材含水率保持在12%左右，本研究所用试材的详细数据如表1所示。

表1 试件的基本信息Tab.1 Basic information of test materials

1.2 基于轴向压缩载荷音板木材的振动和声学试验

模拟音板木材在使用过程中约束以及轴向压缩载荷的情况，对其进行振动和声学测试，测试原理示意如图1所示。试材受到的压缩载荷方向与其纹理方向平行。通过预载荷试验，将试件变形控制在弹性形变阶段，并且不会出现滑块以及端部压溃，最终确定最大施压载荷为1 600 N。

图1 振动和声学试验原理示意图Fig.1 Schematic diagram of the principle of acoustic vibration test

本试验在200～1 600 N轴向压缩载荷区间选取8个轴向压缩梯度，每个梯度中每一树种设置9组重复试验；试验条件采用分级施压的形式，利用电子万能力学试验机(AG-10TA)，通过预先设置的加载应用程序，施压载荷以200 N为步长，对试件施加的载荷和时间的关系，如图2所示。为尽量避免木材蠕变对本试验的影响，每次保压阶段均为180 s，在保压阶段利用双通道快速傅里叶分析仪(CF-5220Z)快速对其进行振动和声学测试。试验中采用冲击力锤对音板木材进行激励，通过每次力锤抬起高度一致，落点一致的方式控制敲击力度和敲击点一致，但仍存在一定测量误差，利用微音器(MI-233)收集声音信号，双通道快速傅里叶分析仪(CF-5220Z)将得到的时域信号转换为频域信号，同时通过时域图和频域图可以计算得出声衰减系数。

图2 轴向压缩载荷与时间的曲线Fig.2 Curve of axial compression load and time

通过双通道快速傅里叶分析仪得到试件各阶段的共振频率，基于固端梁的振动原理[21-22]，得出轴向压缩载荷下音板木材动弹性模量的式(1)

(1)

式(1)未考虑材料阻尼的存在。受外力作用而振动的木材，当外力消失后，由于阻尼的存在，振幅随时间的增大呈负指数规律衰减，如图3所示。因此无阻尼的固有频率要高于实际测试的共振频率[23]。对于这种情况有关学者引入对数衰减系数δ，其计算式如下

图3 固端梁的阻尼振动波形Fig.3 Damped vibration waveform of fixed-end beam

(2)

式中:A1、An、An-1分别为阻尼正弦波的第一、第n-1和第n个振幅；f1为无阻尼梁第一固有频率；fτ为测试得到的第一共振频率；φ为材料的阻尼比。

式(2)通过简单的数学推导可以得到共振频率和固有频率的关系的式(3)。

(3)

将式(3)代入式(1)得到最终固端梁的动弹性模量的计算式(4)

(4)

式中:Ed为梁的动态弹性模量，Pa；fτ为测得的梁的第一阶固有频率，Hz；L为梁的有效长度，cm；I为梁的惯性矩，cm4；A为梁的横截面面积，cm2；ρ为梁的密度，g/cm3；P为轴向载荷，kN。

比动弹性模量是声学参数的重要评价指标之一，根据上述公式，其计算式如下

E/ρ=Ed/ρ

(5)

式中,Ed为试材的动态弹性模量，GPa。

声阻抗W对于木材与其他介质接触界面发生的声音的阻力具有决定意义，其计算式为

(6)

木材在自由振动的时候，能量不断衰减直至消失，能量的衰减分为两部分:一部分是以声波的形式传播到空气中，用声辐射品质常数R表示，其计算为式(7)；另一部分由于声音在内部传播摩擦生热而损失，这部分用损耗角正切tanσ表示，其计算为

(7)

tanσ=δ/π

(8)

式中，δ为对数衰减系数。

为了评价振动能量转换为声音的效率，有关学者引入了声转换效率ACE，其计算公式为

ACE=R/δ

(9)

即使同株木材同一部位的采取试样，其声学性能以及力学性能也会存在一定差异，在测量时不可避免的存在误差，因此同组数据会存在差异。试验中的数据通过IBM SPSS Statistics，Version 23等数据分析软件，对其进行均值、相关性、离散程度的分析，探究振动和声学参数与轴向压缩载荷的趋势和规律。

2 试验结果与分析

2.1 力学试验分析

通过力学试验机得到轴向压缩载荷与形变量的数据，提取其中每200 N的形变量，得到其轴向压缩载荷与形变量的关系，如图4所示。

从图4中可以发现:泡桐和云杉的形变量与轴向压缩载荷呈显著的线性正相关，相关系数r在0.996 0以上。表明在0～1 600 N内，泡桐和云杉的主要形变形式为弹性形变，符合试验预期。轴向压缩载荷每增大200 N，泡桐、云杉形变量平均增加0.06 mm、0.04 mm；相较于有效长度L平均增加了0.024%、0.016%。结果表明云杉变形程度更小，抵抗变形能力优于泡桐。

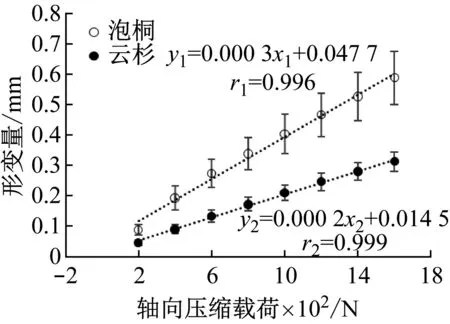
图4 轴向压缩载荷与形变量的关系Fig.4 Relation between axial compression load and shape variable

2.2 轴向压缩载荷与共振频率的关系

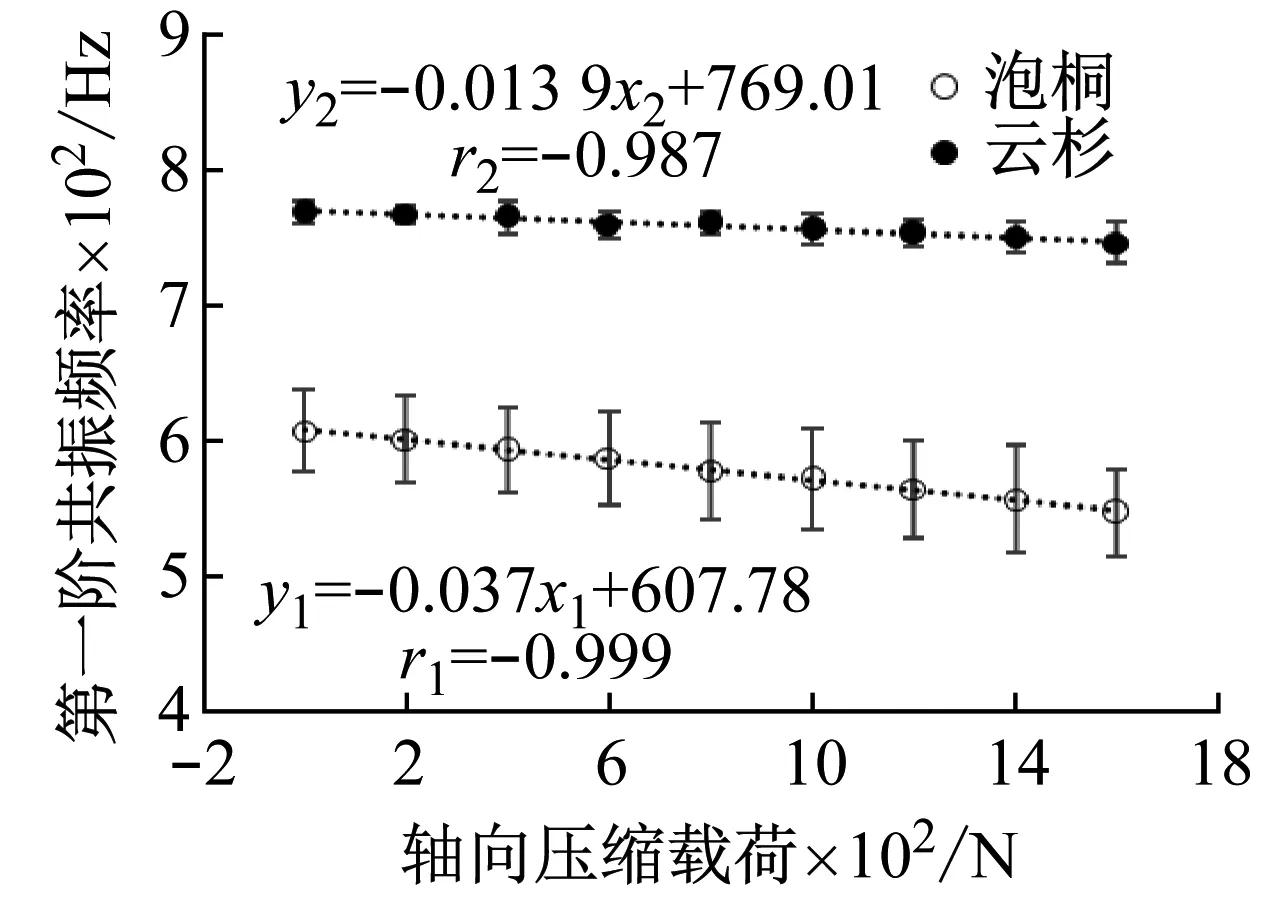
通过试验得到不同轴向压缩载荷作用下音板木材的共振频率，前两阶共振频率变化规律，如图5所示。从图5中可以看出：随着轴向压缩载荷的增大，前两阶共振频率均呈明显的减小趋势，在之前Chopra等对轴压梁的理论研究以及Valle等[24]对轴压梁模拟试验中均得到类似的变化趋势。共振频率的减小是由于试件在轴向压缩载荷作用下，预应力的存在，材料刚度降低，从而使结构的共振频率降低。

从图5中可以看出:泡桐和云杉音板木材的第一、第二阶共振频率与轴向压缩载荷呈显著的线性负相关，相关系数r均在-0.93以下。随着轴向压缩载荷的增加，共振频率呈规律性下降，轴向压缩载荷每增大200 N，泡桐的第一、第二阶共振频率分别平均下降1.22%、0.41%；云杉第一、第二阶共振频率分别平均下降0.36%、0.13%。结果表明:泡桐的共振频率下降趋势要略快于云杉，这是因为云杉作为针叶材，木材结构质密，没有导管以及较多的薄壁组织，轴向压缩载荷对云杉的结构变化影响较小，材料刚度变化程度同样要小于泡桐。

2.3 轴向压缩载荷对声学参数的影响

2.3.1 轴向压缩载荷与比动弹性模量

比动态弹性模量E/ρ是材料动态弹性模量与密度的比值，是评价材料振动声学性能的重要指标，比动态弹性模量越大，其振动声学性能越好[25]。云杉和泡桐的动态E/ρ与轴向压缩载荷之间的关系,如图6所示。

从图6中可以看出:E/ρ与轴向压缩载荷具有显著的线性负相关。泡桐和云杉的比动态弹性模量随轴向压缩载荷的增加，呈明显的下降趋势。轴向压缩载荷每增大200 N，泡桐、云杉的比动弹性模量平均减小3.2%、1.6%。结果表明:随着轴向压缩载荷作用的增大，云杉的比动态弹性模量变化较小，振动声学性能更加稳定。这是因为云杉作为一种针叶材，抵抗压力变形的能力要优于泡桐，木材结构不易改变。

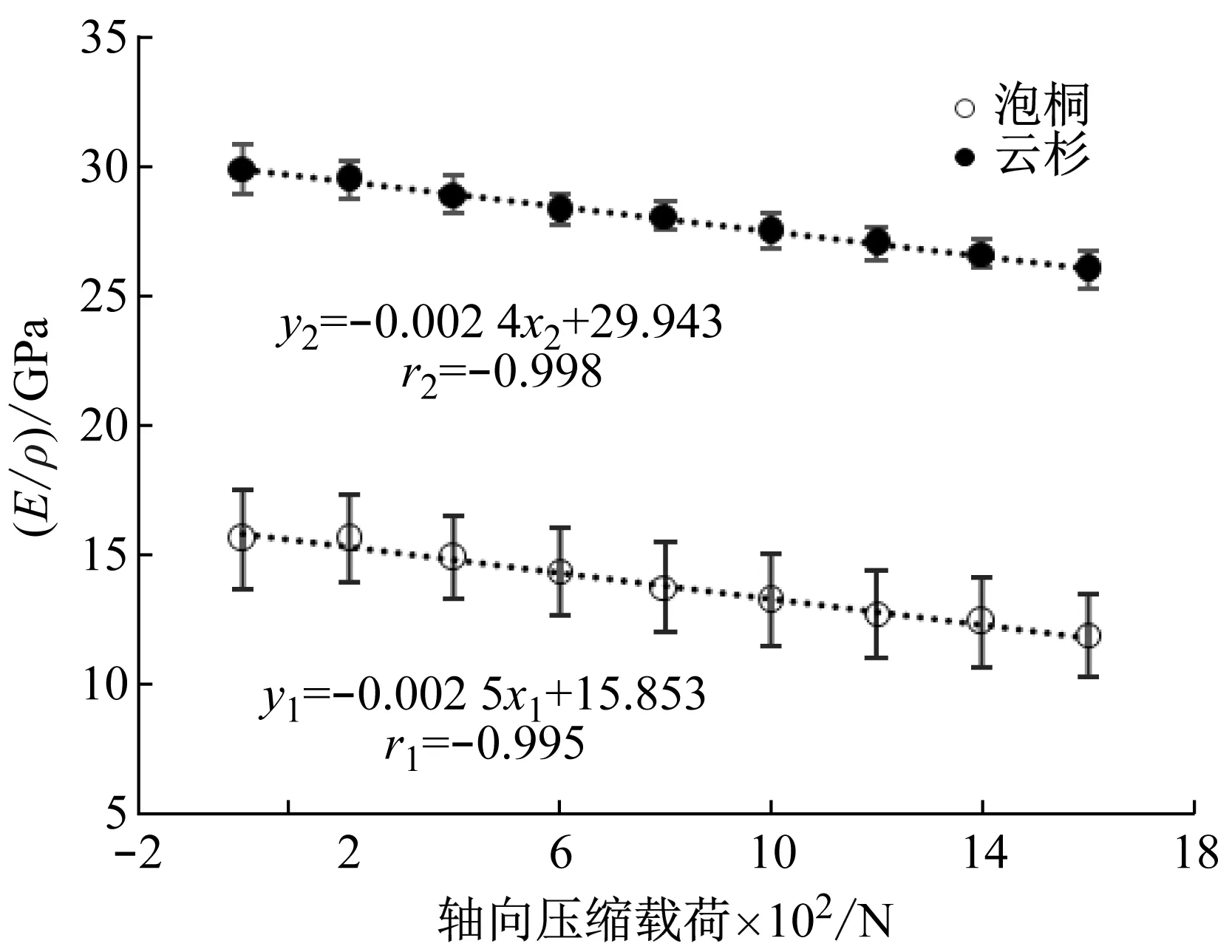
图6 轴向压缩载荷对E/ρ的影响Fig.6 Effect of axial compression load on E/ρ

2.3.2 轴向压缩载荷与声辐射品质常数

声辐射品质常数R是用来评价材料的声辐射品能力，从声辐射品质定义来看，是木材因辐射声而衰减时振动的量度，较高的R值的材料可以产生更加响亮的声音。泡桐和云杉在轴向压缩载荷作用下的R值变化，如图7所示。

从图7可以看出：声辐射品质常数R与轴向压缩载荷同样呈极其显著的线性负相关，其相关系数在-0.98以下，轴向压缩载荷每增大200 N，泡桐、云杉的R值平均降低1.30%、0.97%。R值降低的原因是轴向压缩载荷作用下泡桐和云杉的细胞壁上出现不同程度的褶皱，是材料内部能量消耗上升，造成损耗角正切的增加，从而使声音辐射到周围的能量下降，声辐射品质常数减小。同时从结果中还发现云杉的R值随着轴向压缩载荷增大而降低的程度略小于泡桐，说明在轴向压缩载荷作用下，云杉的声学稳定性更好。

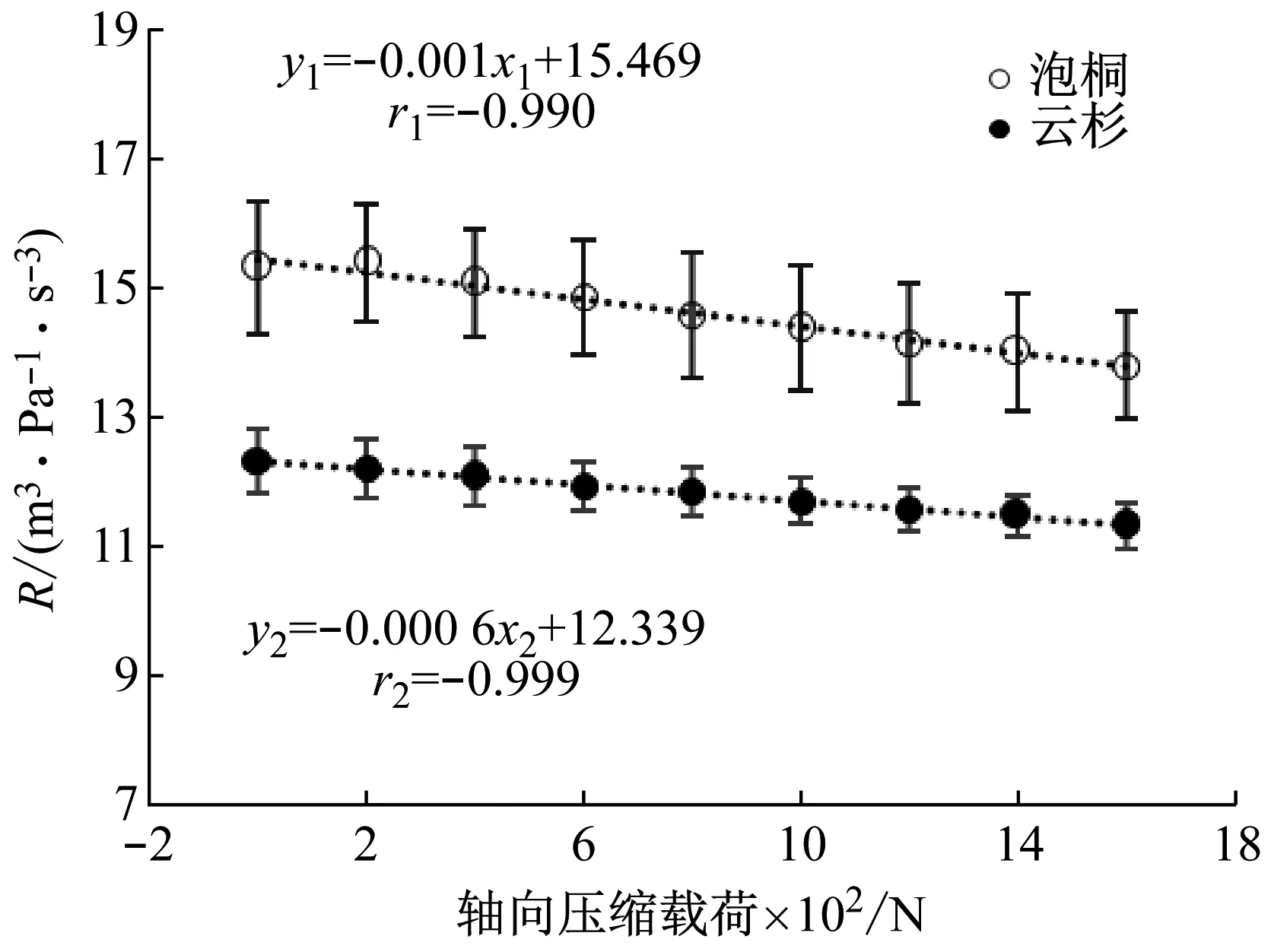
图7 轴向压缩载荷对R的影响Fig.7 Effect of axial compression load on R

2.3.3 轴向压缩载荷与损耗角正切

损耗角正切tanσ是因为声波在木材内传播会引起摩擦，从而引起的能量损耗功率。损耗角正切低说明声音在试件中振动能量衰减速率慢，有利于维持一定的余音，使声音听起来饱满，是评价音板木材品质优劣标准之一[26]。本试验得到的不同轴压载荷下音板木材的损耗角正切，如图8所示。

图8 轴向压缩载荷对tan σ的影响Fig.8 Effects of axial compression loads on tan σ

从图8中可以看出:损耗角正切与轴向压缩载荷呈较强的线性正相关。随着轴向压缩载荷的增大，泡桐和云杉的损耗角正切均呈明显的增大趋势，其相关系数r均在0.96以上。轴向压缩载荷每增大200 N，泡桐、云杉的损耗角正切平均增加11.76%、8.81%。损耗角正切的增加是因为泡桐在轴向压缩载荷的作用下，导管、木纤维以及薄壁组织有一定程度的皱缩,如图9(a)所示，云杉的管胞发生褶皱，如图9(b)所示，这些细胞的皱缩增大了声波在木材中传导的阻力，使因摩擦消耗的能量增加，从而使损耗角正切随轴向压缩载荷的增大而增加，同时也会使振动频率下降,如图9所示。

(a)

图9 未处理材和顺纹压缩材的SEM图Fig.9 SEM drawings of raw andgrain compressed materials

2.3.4 轴向压缩载荷与声转换效率

声转换效率ACE是振动能量转换为声音能量的效率，是对数衰减和声学品质常数的比值[27]。较高的声转换效率ACE对于音板木材至关重要。泡桐和云杉在不同的轴向压缩载荷作用下声转换效率ACE的变化如图10所示。

图10 轴向压缩载荷对ACE的影响Fig.10 Effects of axial compression loads onACE

从图10中可以看出：轴向压缩载荷与ACE同样呈显著的线性负相关，相关系数在-0.96以下，随着轴向压缩载荷的增加，ACE不断下降。轴向压缩每增大200 N，泡桐、云杉的ACE平均减小6.70%、6.56%。ACE减小的主要原因是在轴向压缩载荷作用下泡桐和云杉在细胞壁上出现的褶皱，使得声学在木材内的摩擦消耗增加，传播到周围的能量减小，从而是声转换效率下降。

2.3.5 轴向压缩载荷与声阻抗

声阻抗W对于当振动能量从一种介质传递到另一种介质时，具有极其重要的意义。对于钢琴，古筝等弦乐器来说，需要较低的声阻抗，低W有利于声音传播到空气中。云杉和泡桐的声阻抗与轴向压缩载荷的关系如图11所示。

从图11可以发现:声阻抗与轴向压缩载荷具有显著的线性负相关，相关系数均为-0.998，且在0.005水平上具有统计学意义。轴向压缩载荷每增大200 N，泡桐、云杉的声阻抗平均减小1.97%、0.66%。

随着轴向压缩载荷的增加，声阻抗呈现减小的趋势，振动声学性能略微增加，但根据前人的研究，比动态弹性模量E/ρ、声辐射品质常数R、声转换效率越大，ACE、损耗角正切tanσ和声阻抗W越小，其材料的振动声学性能越优良[25]，这4个振动声学参数对于振动声学性能的影响权重要远大于声阻抗。因此根据上述分析，轴向压缩载荷不断增大，音板木材的整体振动声学性能呈下降的趋势。

3 电子扫描电镜分析

利用用电子扫面显微镜对顺纹压缩前后同一云杉和泡桐试件的微观构造进行观察，结果如图9所示。从电子扫面显微镜图中可以看出未顺纹压缩处理前泡桐的导管以及木纤维通直无褶皱(见图9(a))，云杉的管胞光滑平整无褶皱(见图9(c))，顺纹压缩后的木材中泡桐试件导管和木纤维同样出现褶皱(见图9(b))，云杉的管胞上出现明显的褶皱(见图9(d))。

细胞壁在单向力作用下的变形包括层间的大分子变形和层间的滑移，并没有发生复杂的化学变化。因此通过第2章的分析以及扫描电镜的观察，可以推测这些褶皱的出现是影响声音信号在木材中的传播的重要原因。褶皱的出现使声音信号在材料内部传播因摩擦损耗的能量加大，从而使木材的频率降低，声衰减系数增大，这与前文轴向压缩载荷对共振频率和各声学参数的影响规律分析结果一致。同时由于轴向压缩载荷的施加，木材内部必然有预应力的存在，使其材料刚度发生改变，这也是影响音板木材的振动声学性能的重要因素。

4 结 果

试验分析了音板木材在轴向压缩载荷作用下振动和声学行为，以及轴向压缩载荷与音板木材材料振动和声学性能的关系，并通过SEM观察，从微观角度初步探讨了影响音板木材振动和声学性能的因素。通过研究得出如下结论：

(1)泡桐和云杉音板木材的共振频率f，随着轴向压缩载荷的增加而减小。轴向压缩载荷每增大200 N，泡桐云杉第一阶共振频率分别下降1.22%、0.36%；第二阶共振频率分别下降0.41%、0.13%。泡桐的共振频率随轴向压缩载荷下降趋势要大于云杉。

(2)振动声学参数与轴向压缩载荷均呈显著的线性关系。轴向压缩载荷每增大200 N，泡桐的比动态弹性模量、声辐射品质常数、声转换效率及声阻抗分别减小3.20%、1.30%、6.70%、1.97%，损耗角正切增加11.76%；云杉的比动态弹性模量、声辐射品质常数、声转换效率及声阻抗分别减小1.60%、0.97%、6.56%、0.66%，损耗角正切增加8.81%。轴向压缩载荷对音板木材的整体振动声学性能具有不利的影响。

(3)在轴向压缩载荷作用下，云杉的各振动和声学参数的变化率均要略小于泡桐，说明云杉音板木材的振动声学性能在轴向压缩载荷作用下具有更加优良的稳定性。这是因为云杉材质硬，在轴向压缩载荷作用下变形较小，结构不易改变。

(4)通过分析以及扫描电子显微镜观察可以得知，在轴向压缩作用下，木材细胞壁上出现不同程度的褶皱，由于褶皱的出现，使声音在木材中的传播损耗能量增加，影响了声音信号的传递，这是音板木材在轴向压缩载荷下其振动和声学性能降低的重要原因，同时预应力的存在也是影响振动和声学性能不可忽视的重要因素。