不同含水率膨胀土动剪切模量特征与原位G-γ衰减曲线确定方法
2021-12-20李甜果孔令伟舒荣军
李甜果,孔令伟,舒荣军
(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071;2.中国科学院大学 工程科学学院,北京 100049)
大量的工程实测数据表明,相当一部分岩土工程中土体在工作荷载下处于小应变状态。如果忽略小应变特性会严重低估土体的刚度,造成预计的变形偏大,无法起到应有预测的作用,同时不得不采用保守的施工来满足设计的要求,造成不必要的资源浪费[1]。Hardin等[2]通过室内动力试验发现土体在应变非常小的情况下表现出非线性,应变在0.001%~1.000%内的土体的非线性性状在许多岩土工程问题中起到了关键的控制作用[3],如基础沉降、开挖面变形预测等。因此,有必要考虑土体刚度在小应变条件下的演化特性。事实上,国内外已对小应变剪切模量特性进行了诸多研究。如Dobry等[4]总结了不同围压、孔隙比、沉积年代等对Gmax、G/Gmax和阻尼比D的影响。谢伟等[5]采用弯曲元系统研究了含水率对路基压实土小应变剪切模量的影响,发现不同含水率下压实度对剪切模量的影响规律。于啸波等[6]研究了不同负温下冻结土的初始剪切模量、剪切模量比和阻尼比非线性曲线的变化规律和模式,发现负温对土的初始模量和剪切模量比影响显著,不同的温度段对土体剪切模量的敏感度不同。孙静等[7-8]研究了固结比对不同种类土最大动剪切模量的影响,结果表明固结比对土动剪切模量具有显著影响。并发现随着固结比增加,黏土的动剪切模量比非线性有一定提高。此外,还有部分学者从其他方面对土体的小应变刚度进行了研究,如孔令伟等[9]研究了湛江黏土动剪切模量的结构损伤效应,探讨考虑了土体结构性损伤影响的动剪切模量表征方法,阐明了结构性损伤对其动剪切模量影响的物理机制,并间接印证了提出表征公式的合理性;杨文保等[10]利用共振柱试验探究了同一类原状土在各应变范围内动剪切模量G随土层深度H的变化规律,提出了分别基于土层深度H和Hardin模型的G预测方法,用以预测各类原状土在不同深度下的Gmax及其在各应变范围内的G。
原位试验具有其他试验不可代替的作用。沈珠江[11]指出:要取得可靠的土质参数,只有通过原位测试。相对而言,对原位小应变剪切模量的研究明显落后于室内试验。剪切波速试验可以直接得到原位最大动剪切模量Gmax,但对于随着应变的增加,具有非线性衰减特征的小应变剪切模量而言显然是无能为力,难以直接获得完整原位G-γ衰减曲线。为解决这一问题,一些学者利用原位试验与室内试验相结合的方法来实现对原位G-γ衰减曲线的预测。Lehane等[12]结合地震圆锥贯入仪试验和扁铲侧胀试验(flat dilatometer test,DMT)推求原位G-γ衰减曲线,Amoroso[13]利用地震波扁铲侧胀试验(seismic dilatometer tests,SDMT)来分别推求砂土和粉质黏土的G-γ衰减曲线,并与DMT、地震圆锥贯入仪试验、自钻旁压试验(self-boring pressuremeter test,SBPT)和室内三轴试验进行对比;李晶晶等[14]提出可以借助室内共振柱的G-γ衰减曲线,结合原位地震波扁铲侧胀试验SDMT试验获得的G0、MDMT和MDV来预测南阳膨胀土原位G-γ衰减曲线。陈树峰等[15]在此基础上,对冻融循环作用下粉质黏土原位动剪切模量及衰减特征进行了研究。但是以上方法本质上都是参照室内试验曲线来实现原位G-γ衰减曲线的预测。参考曲线的选取直接影响预测结果,然而以上研究都没有明确的参考曲线选取准则,导致参考曲线的选择具有较大的主观性,最终造成对原位G-γ衰减曲线的预测存在较大不确定性。安然等[16]则利用SBPT与SDMT两种试验结果,通过拟合获得花岗岩残积土原位G-γ衰减曲线,更接近真实原位G-γ衰减曲线,但必须具有SBPT的数据,在推广上具有局限性。同时,在自然界中,土的形成过程十分复杂,不同土类、相同土的不同存在状态(应力[17]、含水率等)都会影响土的小应变刚度特性,这些因素对原位G-γ衰减曲线的预测是否存在影响,仍需进一步研究。
总的来说,对原位G-γ衰减曲线的研究,远远落后于工程应用的需要,尤其是对特殊土的研究。目前,我国各个城市正在大规模建设地铁,这与土的小应变刚度特性息息相关。膨胀土作为一种特殊土,广泛分布于我国的云南、广西、河南、山东、黑龙江等20多个省市,已建成、在建及将建的工程均需穿越大量的膨胀土地段,因此,了解膨胀土的小应变刚度特性十分必要。考虑到含水率变化对膨胀土结构的影响较大,本文以佳木斯弱膨胀土为研究对象,研究不同含水率膨胀土的小应变刚度变化规律,同时结合原位SDMT试验和室内原状土共振柱试验,对膨胀土原位G-γ衰减曲线进行预测,为相关方面的研究提供理论依据与数据支持。
1 试验方案与土样
1.1 试验场地与土样基本特性
原位试验场地位于黑龙江省佳木斯市某在建货运中心附近,取样点靠近原位试验场地旁的裸露边坡,距坡顶4 m,该场地分布有大量具有胀缩性的弱膨胀土。采用刻槽法取新鲜完整块状土样密封装箱运存,试验仪器和土样如图1所示。土样有关的基本物理参数试验结果,如表1所示,从基本物理参数可得,该土样的液限wL和塑限wp分别为wL=43.8%,wp=27.6%,自由膨胀率δ=55%。小于0.005 mm的黏粒含量占40.1%,小于0.001 mm的颗粒含量占22%。表2为采用X射线粉晶衍射仪试验得到的佳木斯弱膨胀土的矿物组成,黏土矿物含量占35%,并且黏土矿物主要是吸水性较强的蒙脱石、伊利石以及伊蒙混层。土的自由膨胀率、黏粒含量、以及矿物组成均在膨胀潜势等级判断标准范围内,属于弱膨胀土[18]。冷冻干燥土样电子显微镜照片,如图2所示。显示原状样具有弱膨胀土的典型特征即原状样结构以扁平状颗粒为主,含片状颗粒和单粒体较多,卷曲片状颗粒少见[19]。
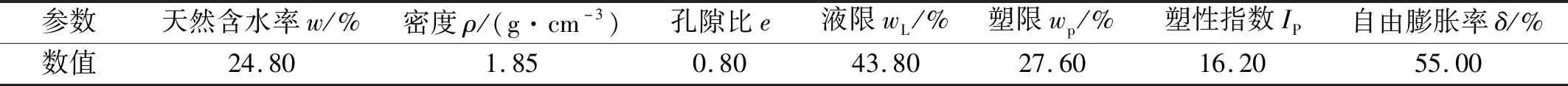
表1 试验土样的基本物理参数Tab.1 Basic physical parameters of tested soils

(1)SDMT试验

表2 试验土样的矿物组成Tab.2 Mineral composition of test soil samples %

(a)
本文试验使用试样为由原位所取块状样沿竖向沉积方向切削制成,是直径50 mm、高100 mm的圆柱状土样,为控制含水率为唯一的变量,试验土样均取自深度相同原状样,并在制样后选择孔隙比相同的土样,所有土样都要在真空缸中进行抽真空饱和,饱和后土样的含水率为30%。特定含水率试样的制备通过质量控制法,根据土样的干密度,计算出特定含水率土样的质量,然后将饱和样放在恒温恒湿箱中缓慢脱湿至该质量,然后用保鲜膜密封土样,放在保湿缸内一周,使土样内部水分分布均匀。本研究中含水率控制为8.5%、17.2%、22.2%、24.8%和30.0%。
1.2 试验方案
1.2.1 共振柱试验
采用的共振柱仪器是英国GDS公司生产的固定-自由型Stokoe共振柱,如图3所示。试验仪器主要由驱动系统、监测系统、排水系统和压力室组成,GDS共振柱是在实心圆柱土样的顶端施加一个振动激励,通过电磁驱动系统产生一个扭转激振或纵向激振,通过测量自由端的运动,获得共振频率f,则剪切波速vs根据下式计算

图3 共振柱试验装置框图[20]Fig.3 Schematic of resonant-vibration column test device[20]
(1)
剪切模量G可由剪切波速vs求得
(2)
式中:G为土样的动剪切模量;ρ为土样的质量密度;f为扭转振动共振频率;H为土样的高度;β为扭转振动频率方程的特征值。
共振柱试验通过逐渐增加激励电压的方式来增加剪应变,本试验激励电压范围为0.005~0.850 V,在一定围压下排水固结稳定后进行试验,固结稳定的标准为轴向变形5 min内不大于0.005 mm。为了研究不同应力对佳木斯弱膨胀土小应变剪切模量的影响,试验围压设置为25 kPa、50 kPa、100 kPa、150 kPa、200 kPa、300 kPa和400 kPa。
1.2.2 地震波扁铲侧胀(SDMT)试验
地震波扁铲侧胀试验在传统扁铲侧胀试验基础上集成了波速测试模块,可同时进行扁铲试验和波速测试,特别适用于研究土体原位小应变刚度及其非线性特征。地震波速模块即在扁铲一端安装相隔0.5 m的两个剪切波接收单元,接收来自地面震源信号,通过两个接收单元与震源距离差和接收到信号的时间差得到剪切波速,通过剪切波速可以推导出小应变剪切模量。扁铲侧胀试验通过探杆将扁平铲形探头和传感器以恒定速率垂直压入土中,达到试验深度后,通过压力源施加压力使扁铲探头上的钢膜片侧向膨胀,分别测得膜片中心侧向膨胀不同距离(分别为0.05 mm和1.10 mm)时的气压值,然后缓慢排气,测得使膜片回缩接触基座时作用在膜片内的气压值,根据压力与变形之间的关系直接或间接地获得土体原位参数。佳木斯原位SDMT试验深度为0~6 m,每0.5 m进行一次试验,共做了两个试验点。
2 试验结果与分析
2.1 不同含水率膨胀土G-γ衰减曲线特征
不同含水率膨胀土在不同围压下的G-γ衰减曲线,如图4所示。由图4可知,不同含水率试样的G-γ衰减曲线具有高度的相似性,动剪切模量G随着剪应变γ的增加呈非线性减小。含水率相同时,膨胀土G-γ衰减曲线随着围压的增加向上移动,表明围压有助于增强土体的动剪切模量。从图4可以看出,相同围压范围内,膨胀土的动剪切模量随着含水率的增加而减小,且含水率越小,曲线覆盖面积越大,围压对动剪切模量的增加作用越明显,表明含水率对膨胀土动剪切模量具有很大的影响作用,原因是膨胀土具有较多的黏土矿物以及明显的失水收缩特性,当含水率较小时,土体吸力较大,在较大吸力的作用下土颗粒之间的接触更加紧密,从而增加了土体的动剪切模量。
(a)w=8.5%
常用的G-γ衰减曲线模型有Hardin-Drnevich方程(式3)、Stokoe方程(式4)和Davidenkov模型(式5)。
(3)
(4)
式中:γ为剪应变;γr为参考剪应变;α为曲率系数。
G(γ)=Gmax[1-f(γ)]
(5)
其中
(6)
式中,γ、A、B为与土性有关的拟合参数。
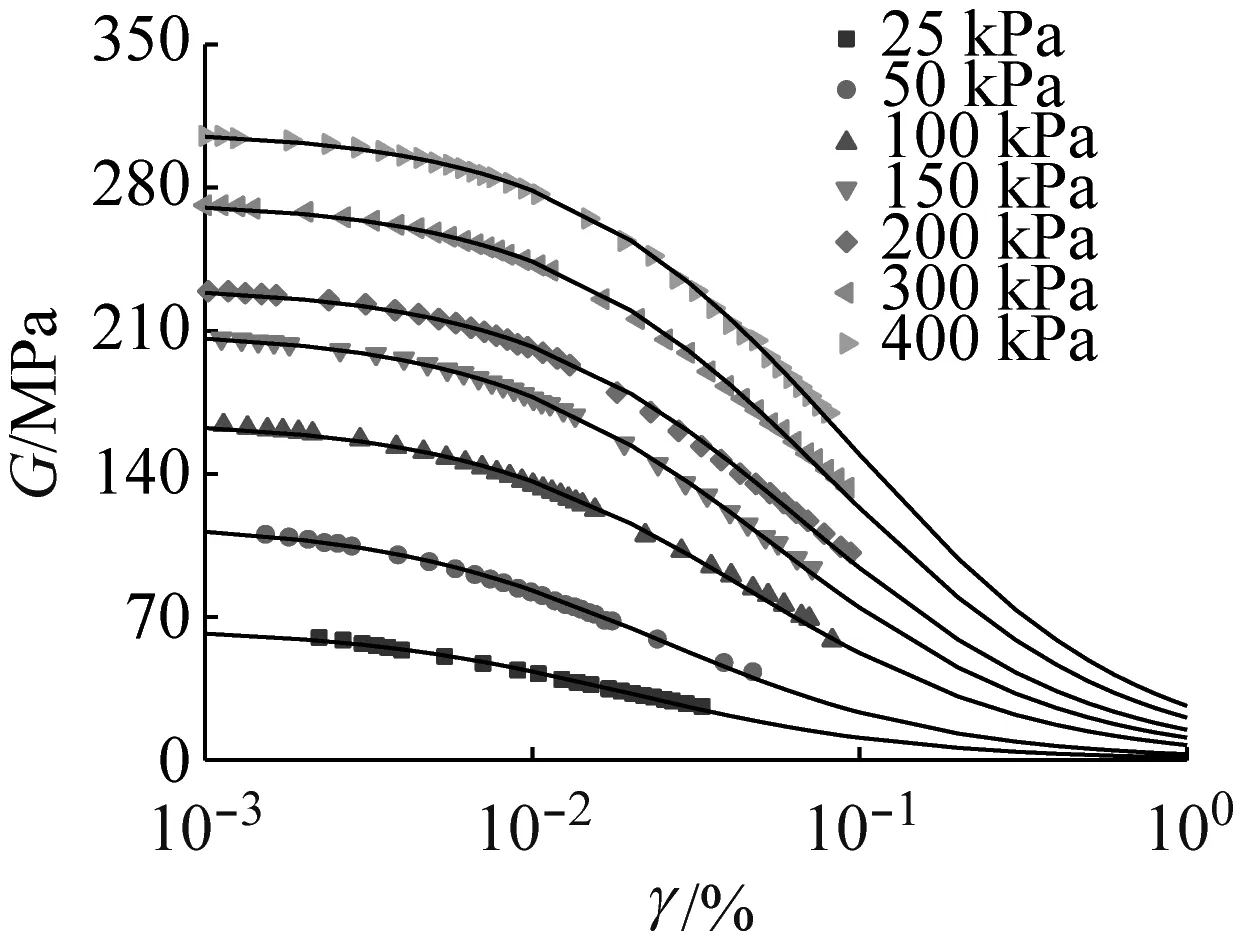
考虑到本文采用的共振柱试验应变范围有限,采用参数较多的模型的高自由度易造成拟合结果的变异性增大,因此使用简单的Hardin-Drnevich方程(式3)对G-γ曲线进行拟合,发现具有很好的拟合效果,R2可达0.976~0.999,各围压下拟合出的最大动剪切模量Gmax、参考剪应变γr,如表3所示。
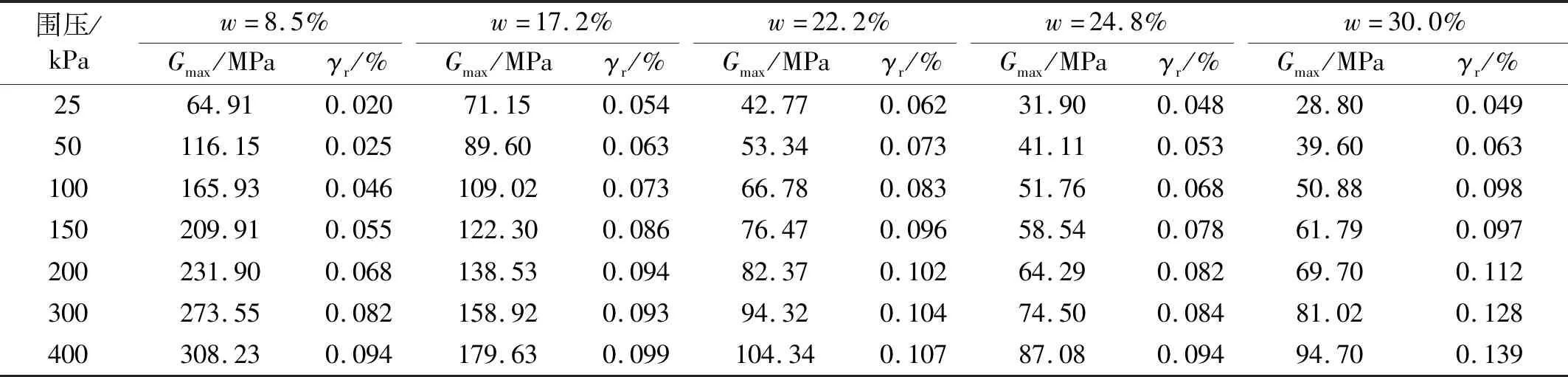
表3 最大动剪切模量Gmax和参考剪应变γrTab.3 Maximum dynamic shear modulus Gmax and reference shear strain γr
2.2 不同含水率膨胀土G/Gmax-γ特征
不同含水率膨胀土的G/Gmax-γ曲线,如图5所示。相同含水率条件下,随着围压的增加,曲线向上移动,表明膨胀土的G/Gmax-γ是与应力状态相关。随着含水率的增加,曲线上移,并且在试验围压范围内,试验点分布带变窄,说明含水率越大,围压对曲线的影响减弱。
为了便于与其他土类进行对比分析,对同一含水率下的所有试验点数据进行拟合,得到在该含水率下的G/Gmax-γ曲线(图5中的点划线)。图6给出了含水率为8.5%和30.0%的膨胀土的拟合曲线(这两条拟合曲线是不同含水率膨胀土的G/Gmax-γ曲线族的下限和上限),并与规范值和袁晓铭等[21]提出的常规土类推荐值进行对比分析,以深入了解不同含水率膨胀土与其他土类的动力特性差异。从图中可以看出,不同含水率膨胀土的G/Gmax-γ曲线差异较大,分布于粉质黏土和黏土的推荐值曲线附近,其中,含水率为30.0%的膨胀土的G/Gmax-γ曲线更接近于黏土,而含水率为8.5%的膨胀土的G/Gmax-γ曲线整体上更接近于粉质黏土。而当剪应变大于0.5%时,含水率为8.5%的膨胀土的G/Gmax-γ曲线更接近于松砂和淤泥。本文中研究的膨胀土可以被归类为粉质黏土,但却具有较高的液限和弱膨胀性,若采用粉质黏土的推荐值,对于低含水率的膨胀土具有较高的准确性,但对于高含水率的膨胀土,使用黏土的推荐值更合适。因此,对于不同含水率膨胀土的动力特性分析,应注重含水率的影响。

(a)w=8.5%

图6 不同类型的土的G/Gmax-γ曲线Fig.6 G/Gmax-γ curves of different types of soil
2.3 不同含水率试样最大动剪切模量Gmax特征
最大动剪切模量Gmax是表征微小应变范围内(γ<1×10-5)土体弹性变形阶段的峰值剪切模量,对土体动力学响应具有重要的意义。最大剪切模量难于直接测量,通常根据小应变模量数据结合剪切模量-应变关系模型计算而来,本文Gmax是根据式(3)对试验数据进行拟合获得。对于正常固结土,影响Gmax的主要因素有围压、孔隙比等,Gmax一般随着围压的增加而增加,随着孔隙比的增加而减小,Hardin and Dmevich基于饱和砂土试验给出了预测最大剪切模量Gmax的经验模型
(7)
式中:Gmax为最大剪切模量,MPa;σ为有效围压,kPa;e为孔隙比;A、a、n为与土体自身性质相关的参数,对于圆粒土三者建议值为6 900,2.17和0.5,而对于角砾土则分别为3 200,2.97和0.5,在饱和状态下,同种土体A、a、n值通常被认为常量。该模型后被推广应用至黏性土、粉土黏土,得到了令人满意的结果。对于不具有特殊性质的一般土而言,仅仅改变含水率对土体积变化影响甚微,孔隙比基本保持不变,可以认为只改变了土的含水率,而未影响土的结构。而对于膨胀土而言,含水率对孔隙比的影响显然不可忽视。原状土保持了最原始的结构,孔隙比和含水率为定值,可以认为原状土是相同的。本研究中为了获得不同含水率“原状样”,需要将原本相同的原状样,经过脱水变为具有不同含水率的“原状样”,由于膨胀土的吸水膨胀失水收缩的特殊性,在这一过程中,因为含水率而改变了孔隙比,而在试验过程中,孔隙比又会因为力的作用产生变化,此时的孔隙比是含水率和力综合作用结果。本质上,力对孔隙比的影响大小是土的结构强度决定的,而对于初始结构相同、含水率不同的土而言,土的结构强度其实是由含水率决定的。因此,为了简化分析,本研究采用具有相同初始孔隙比饱和样进行脱湿,而由于试样脱湿导致的孔隙比变化以及在围压的作用下引起的孔隙比变化,都视为含水率变化对孔隙比的影响,这样对最大动剪切模量的影响就可以不考虑孔隙比这一因素,只需要关注含水率的影响。因此,基于这一考虑,在 Hardin 公式的基础上,综合描述围压和含水率对弱膨胀土最大剪切模量的影响,式(7)可以改写为
Gmax=Af(w)σn
(8)
式中:σ为有效围压;f(w)为与含水率有关的函数表达式;A、n为与土体自身性质相关的参数。
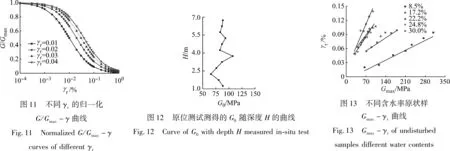
不同围压下,最大动剪切模量Gmax随含水率的变化曲线如图7所示。由图7可知,随着围压的增加,最大动剪切模量Gmax增加,含水率越小,不同围压下的Gmax相差越大。值得注意的是,Gmax-w曲线存在一个拐点含水率wt=24.8%,当含水率小于拐点含水率时,随着含水率的增加,Gmax快速降低;当含水率大于拐点含水率时,Gmax基本保持不变,这反映出含水率对动剪切模量的分阶段性。为了使分析更加简单化,根据Gmax-w曲线在不同围压下的形态相似性,用饱和样的最大动剪切模量Gmaxs对Gmax进行归一化处理,归一化后的Gmax/Gmaxs-w曲线如图8所示,可以分为两个阶段分析:①当w≥wt时,认为土样Gmax保持不变,与饱和试样的最大动剪切模量Gmaxs相等;②当w Gmax/Gmaxs=(aw+b) (9) 式中,a、b为拟合参数。将Gmaxs移到式子右边,式(9)可以写为 Gmax=(aw+b)Gmaxs (10) 饱和样的最大动剪切模量Gmaxs随围压的变化曲线如图9所示,可以表示为 Gmaxs=Aσn (11) 将式(11)代入式(10),则可以得到当w Gmax=A(aw+b)σn (12) 结合w≥wt时Gmax=Gmaxs,因此适合膨胀土的预测模型可由式(13)表示 (13) 根据试验数据结果,佳木斯弱膨胀土可以表示为 使用该公式对不同围压和含水率的Gmax进行预测,与实际值进行比较发现具有良好的预测效果,如图10所示。 土体的G-γ衰减曲线是描述土体动剪切模量随剪应变变化的曲线,对G-γ衰减曲线进行归一化后的G/Gmax-γ拟合曲线可以方便地对不同试样的衰减曲线进行对比分析,其中参考剪应变γr的大小决定着衰减曲线的衰减速率,γr的不同就意味着归一化后的G/Gmax-γ拟合曲线形态不同,图11为不同γr值的G/Gmax-γ曲线,从图11可以看出,随着γr的增加,G/Gmax-γ曲线上移,衰减速率变小。 原位试验由于场地的复杂以及可以使用的仪器有限,难以直接获得原位数据,因此,通常采用将原状样加荷的方法来模拟原位土体,使用室内试验模拟原位应力时,通常认为土体所处应力σ=γH,H为土体埋深,γ为土体容重,一般取20 kN/m3。为了探寻这一方法的准确性,对饱和原状样施加50 kPa和100 kPa的围压进行共振柱试验,来模拟原位2.5 m和5.0 m处土体应力,原位地震波所得G0随深度的变化曲线如图12所示,原位SDMT试验获得2.5 m和5.0 m剪切模量G0为70.90 MPa和90.25 MPa(原位试验场地6 m内土样饱和度在95%以上,基本处于饱和状态)。由表3数据可知,室内饱和试样在50 kPa和100 kPa情况下,所得Gmax只有39.80 MPa和50.88 MPa,远远小于原位试验结果,造成这种现象的原因:一方面是对原位应力模拟的失真造成的,低估了原位应力的大小;另一方面是原位土体的是在非均等应力下固结的,而室内试验多采用均等固结。孙静等的研究发现,粉质黏土不同固结比的最大动剪切模量是等向固结下的125%。由此可知,室内试验会严重低估原位土体的刚度,采用室内试验结果过于保守,增加不必要的资源浪费。为解决这一问题,一些学者利用原位试验与室内试验相结合的方法来实现对原位G-γ衰减曲线的预测。李晶晶等的研究提出了一种预测原位G-γ衰减曲线的方法。本文在李晶晶等的研究提出的原位G-γ衰减曲线基础上,结合共振柱试验规律对原位G-γ衰减曲线推求方法进行了改进。李晶晶等研究的推求方法同下。 步骤1由现场SDMT试验中地震波速模块获得原位动剪切模量G0以及相应的剪应变γ0,其中γ0代表极小应变,可取0.001%。 步骤2通过SDMT试验扁铲侧胀模块试验结果经数据分析得到MDMT和MDV,以及GDMT和GDV。 步骤3以室内G/Gmax-γ曲线为参考,找到与GDMT/G0和GDV/G0相等时对应的工作应变γDMT和操作应变γDV。 步骤4选取合适的拟合公式,通过得到的3个点(G0,γ0)、(GDMT,γDMT)、(GDV,γDV)拟合获得现场原位G-γ衰减曲线,相关计算公式为 (14) (15) (16) 式中:ρ为土体天然密度;μ为泊松比,取0.25;RM为与扁铲土性指数ID和水平应力指数KD相关的系数;ED为扁铲侧胀模量。 这一预测原位G-γ衰减曲线的方法,由于利用了原位地震波扁铲侧胀试验结果,使预测数据更加贴近真实情况,尤其是在极小应变条件下,采用了地震波数据,几乎可以真实反映原位最大动剪切模量。而该方法存在一个较大的问题,在步骤3中,李晶晶等的研究直接采用室内试验所得归一化G/Gmax-γ曲线作为推求出的原位G-γ衰减曲线的参考曲线,在认为原位G-γ衰减曲线与室内G-γ衰减曲线具有相同的形态特征的前提下,借助室内试验曲线来获得原位工作应变γDMT和操作应变γDV。因此该方法推求出的原位G-γ衰减曲线受室内参考曲线的影响很大,使用该方法就必须获得相对原位应力状态下土体的室内G-γ衰减曲线作为参考曲线,一旦室内试验参考曲线选取不合适,原位预测结果将产生很大的差异,李晶晶等的研究也有提出该缺点。若土样的归一化G/Gmax-γ曲线与围压无关(不同围压下G-γ衰减曲线的γr相同),则所有应力状态下的归一化G/Gmax-γ曲线为同一条曲线,利用该曲线作为参考曲线求出原位不同应力状态的G-γ衰减曲线是合适的。而佳木斯弱膨胀土在不同应力状态和不同含水率条件下,γr不同,尤其是不同应力状态试样,γr相差较大,而原位试验中,很难确定土体所处的应力状态,应力状态的不确定性大大加大了室内参考曲线的选取难度,因此必须提出一种有助于选取室内参考曲线的依据,不能单纯认为某一压力下室内G-γ衰减曲线与原位G-γ衰减曲线具有相同的曲线形态,这样将严重影响对原位G-γ衰减曲线预测的准确性。 在对佳木斯弱膨胀土的试验中发现,当含水率相同时,拟合参数Gmax和γr具有良好的线性关系,如图13所示。此关系不受土体应力状态影响,也就是说,无论土体所处地应力为多少,其最大动剪切模量γr和Gmax呈线性关系。从图13还可以看出,随着含水率的增加,γr越大,γr-Gmax关系曲线斜率越大,说明G-γ曲线的衰减规律受含水率的影响,土样越湿,G的衰减速率越慢。根据这一规律,若已知原位土样含水率与最大动剪切模量Gmax,则可根据室内相同含水率原状土样Gmax和γr之间的线性关系,推求出与原位Gmax对应的参考剪应变γr,避免了选取室内参考曲线时的盲目性,为推求原位G-γ曲线提供了支撑依据。 以佳木斯原位SDMT试验为例,对改进的方法进行讨论。通过SDMT试验扁铲侧胀模块试验结果经数据分析得到GDMT和GDV,由SDMT试验中地震波速模块获得原位动剪切模量G0以及相应的剪应变γ0,经原位最大剪切模量G0归一化成功得到GDMT/G0和GDV/G0值,最后依据Gmax和γr具有良好的线性关系,获得原位G0相应参考衰减曲线拟合参数γr,找到与GDMT/G0和GDV/G0相等时对应的工作应变γDMT和操作应变γDV。最后,根据获得的(G0,γ0)、(GDMT,γDMT)、(GDV,γDV)利用式(3)拟合得出原位G-γ衰减曲线。以室内饱和样50 kPa和100 kPa共振柱试验为例,由李晶晶等的方法推算出原位G-γ衰减曲线和改进后的衰减曲线以及相应围压室内试验衰减曲线,如图14所示。由图14可知,两种方法得到的原位衰减曲线均高于原位应力下室内试验获得的结果,说明使用室内试验结果表示原位土体特性具有较大的误差,该误差主要有两部分原因:一是室内试验土样在取样、运输和削样过程中对原状样有一定的扰动;第二个原因也是最大的原因,即对原位应力的模拟失真,使用容重与深度的乘积作为原位应力太过于理想和粗糙。当应变较小时,这两种方法得到的动剪切模量差异小,与原位剪切波速试验获得值相近,但是随着剪应变的增加,同等应变条件下,改进方法推求出的动剪切模量更大,衰减速率更小,安然等利用SBPT与SDMT获得完整的土体原位G-γ衰减曲线衰减速率较李晶晶等的方法也较小,进一步间接说明改进方法的可靠性。 图14 剪切模量G随剪应变γ变化曲线Fig.14 Curves of shear modulus G with shear strain γ 本文结合原位SDMT试验和室内RCT试验,研究了不同含水率弱膨胀土的小应变动剪切模量特性,并根据室内试验规律,提出了一种预测原位G-γ衰减曲线的方法,主要结论如下: (1)开展不同含水率佳木斯弱膨胀土原状样的共振柱试验,对膨胀土的小应变动剪切模量有了较深入的了解。试验发现Hardin-Drnevich方程对弱膨胀土G-γ衰减曲线具有很好的拟合效果,不同含水率膨胀土动剪切模量G随着剪应变γ的增加,具有明显的非线性衰减特征。含水率对动剪切模量G影响显著,随着含水率的增加G具有逐渐减小的趋势。 (2)最大动剪切模量Gmax随着围压的增加而增加,含水率越小,Gmax增加越多。Gmax/Gmaxs-w曲线与围压无关,且存在一个拐点含水率,当含水率大于等于拐点含水率时,Gmax等于饱和样的Gmaxs。当含水率小于拐点含水率时,Gmax随着含水率的增加快速减小;考虑到相同初始状态膨胀土脱湿至不同含水率状态下,体积发生明显变化,提出了适用于不同含水率膨胀土Gmax的预测模型,预测值与实际值较为吻合。 (3)相同含水率条件下,膨胀土的Gmax和γr具有良好的线性关系,根据这个规律提出的改进的原位G-γ衰减曲线推求方法为室内参考曲线的选取提供了依据,提高了原位预测的准确性。3 不同含水率膨胀土的原位G-γ衰减曲线推求方法

4 结 论
