基于柔性软开关的主动配电网两阶段鲁棒优化运行

任辰，刘浪，周健，时珊珊，田书欣，符杨

（1. 国网上海市电力公司电力科学研究院，上海市 虹口区 200437；2.上海电力大学 电气工程学院，上海市 杨浦区 200090）

0 引言

近年来，基于可再生能源的分布式发电机(distributed generator, DG)在配电网中得到迅速发展[1]。高渗透率的DG 不断接入，使得配电网从结构到运行方式都发生了巨大变化，导致配电网的潮流、无功与电压控制[2]等问题更加突出。光伏、风机等间歇式能源具有很强的不确定性，往往导致运行中出现线路功率大幅波动以及电压波动、越限等诸多问题，进而带来系统运行损耗增加、运行经济性下降、出现安全越限等不良后果，严重时甚至可能因过载而引发设备故障导致停运，造成巨大的经济损失[3]。为了解决间歇性DG 高渗透率带来的问题，传统的配电网调整手段主要以一次设备为基础，如有载调压变压器(on-load tap changer，OLTC)[4]、可调电容器组(capacitor banks，CB)[5]、联络开关[6-7]等。其中OLTC 的分接头调整、CB 的投切和联络开关的重构都受响应慢和电压离散调节的限制，难以满足主动配电网中DG 频繁波动时电压快速控制、潮流连续调节的要求。然而，基于软开关(soft open point，SOP)的柔性互联技术显著增强了系统运行的可控性和灵活性。与传统的开关操作相比，SOP 可以精确地控制有功功率和无功功率的流动，降低运行成本，避免频繁开关动作造成的风险。SOP 是一种新的电力电子设备，可以实现馈线之间的灵活连接。SOP 的应用将显著促进主动配电网的经济性、灵活性和可靠性。

目前关于SOP 在配电网运行的应用，国内外已经做了大量的研究。文献[8-9]表明，SOP 通过降低网络损失、改善电压分布和平衡主动配电网中的馈线负载，显著提高了DG 的调节能力。考虑到SOP 和电压调节装置的协调，文献[10]采用基于凸规划的方法有效地消除了系统运行中的电压越限现象；文献[11]对DG 和储能系统进行了有功与无功优化，以实现在一段时间内配电网中系统运行网损最小和DG 利用率最大。以上SOP 运行策略的制定主要依赖于预测数据，由于实际运行情况的不确定性问题，SOP 的确定性运行策略可能会导致电压偏移量显著增加，甚至导致电压违反安全运行约束，因此需要处理这些不确定性，以确保系统运行的可行性和可靠性。

为解决DG 出力与负荷需求的不确定性，并充分利用SOP 的优点，本文以配电网运行总成本最小为目标，建立主动配电网两阶段鲁棒的SOP与联络开关协同优化运行模型。此外，还分析了不确定性预算因子和不确定性偏差范围对目标值的影响，为决策者提供经济性和安全性之间的权衡。最后采用改进的IEEE 33 节点算例验证本文方法的有效性与安全性。

1 SOP 的主要功能与数学模型

1.1 SOP 的主要功能

本文以背靠背电压源型换流器(back to back voltage source converter，B2B VSC)为实现方式的SOP 为研究对象，其拓扑结构如图1 所示。

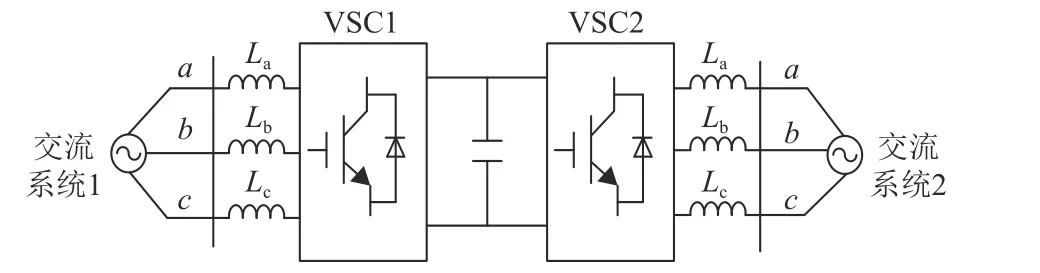
图1 基于B2B VSC 的SOP 拓扑结构Fig. 1 SOP topological structure based on back to back voltage source converter

SOP 主要安装于传统联络开关处，可实现线路间有功功率传输的实时连续控制，并提供相应无功支撑, 如图2 所示。

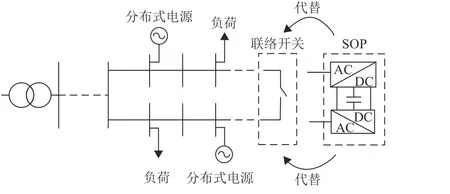
图2 SOP 接入位置Fig. 2 Installation position of SOP

1.2 SOP 模型

本文在正常运行时选择SOP 的定直流电压控制(PQ-VdcQ)方式[12]，SOP 运行中的变量主要有：SOP 两端输出的有功功率Pi和Pj以及两端输出的无功功率Qi和Qj。需满足以下约束。

1）SOP 有功功率约束。

2 含SOP 的配电网重构模型

2.1 目标函数

本文以最小总运行成本作为目标函数，系统的总运行成本由功率损耗成本和开关动作成本2部分组成，其表述为

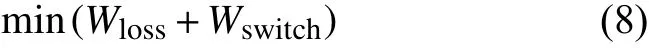
式中：Wloss表示功率损耗成本；Wswitch表示开关动作成本。

功率损耗成本Wloss包括网损成本以及SOP功率传输损耗成本，总功率损耗成本可表示为

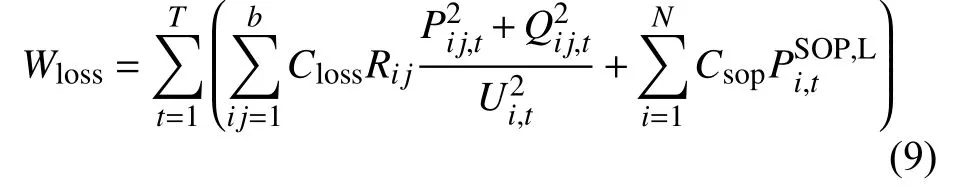
式中：T表示总时间周期；b表示所有线路总数；N表示配电网节点总数；Rij为支路ij的电阻值；Pij,t和Qij,t分别表示在t时段流过支路ij的有功功率和无功功率；Ui,t为t时段节点i的电压幅值；Closs和Csop分别表示网损费用和SOP 运行费用。

开关动作成本Wswitch可表示为

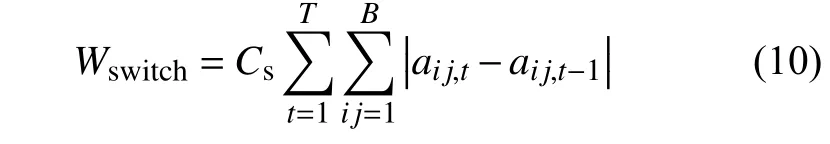
式中：B为总的开关数；Cs为开关操作一次的费用；aij,t表示线路ij上的开关在t时段的开断状态，aij,t=1，表示开关闭合，aij,t=0，表示开关断开。

2.2 约束条件

1）系统潮流约束。

本文参照文献[13]建立Distflow 潮流模型，Distflow 潮流模型是一种从支路功率出发建立的潮流方程，相比于传统的基于节点功率的潮流计算法，它更适用于辐射状配电系统的潮流计算。

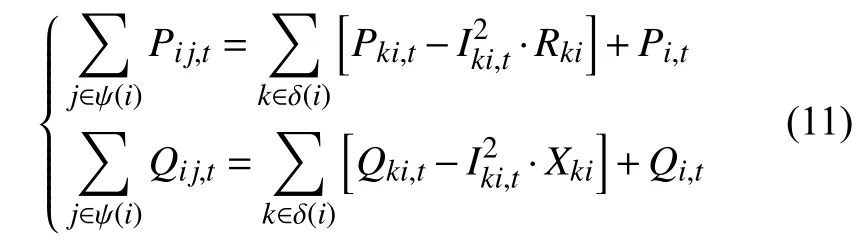
3）SOP 约束。

公式(1)—(7)。

4）开关动作次数约束。

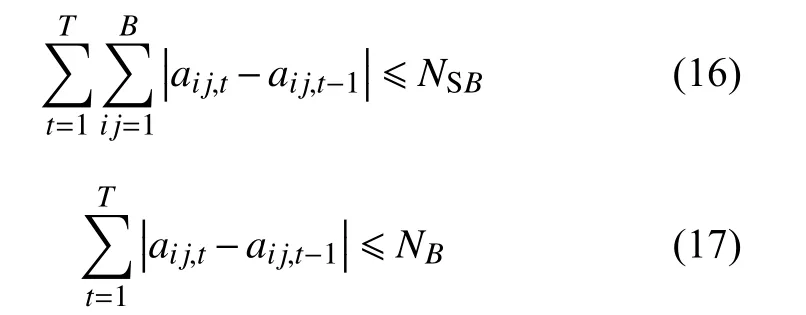
式中：NSB、NB分别为优化周期内最大允许的总开关操作次数和单个开关最大允许操作次数。

针对配电网中的开关，定义布尔型变量aij,t用于表征配电网中的各个开关的开断情况，即表示线路ij上的分段开关的开断状态。使得DistFlow潮流约束对于拓扑结构灵活变换的配电网优化运行策略适用性更强。当线路上的开关处于闭合状态时，线路正常传输功率，而当开关处于断开状态时，则会使线路上的功率传输降为零，此时呈现出的特征为：断开开关的线路两端节点电压不再满足式(13)、并且线路电流降低为零。因此可将式(13)的数学模型进行如下表征，使其适用于拓扑多变的复杂配电网

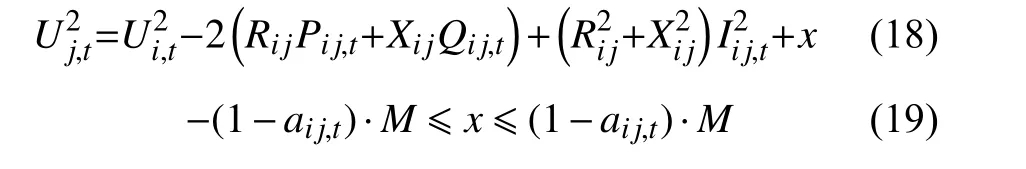
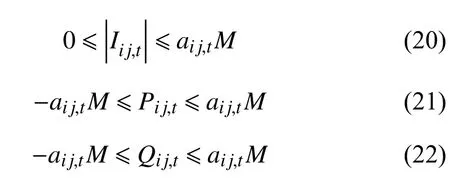
式中：M表示一个很大的正数，当aij,t=1 时，即线路开关闭合，此时的式(18)同式(13)一致，且根据式(20)—(22)可知此时支路ij的电流以及功率均不受限，保证正常运行状态；反之当aij,t=0 时，线路两侧电压解耦，且在夹逼定理的作用下流过线路的电流及功率均被限为零，此时式(18)恒成立。在建立模型时不妨按照式(18)—(22)建立所有的支路模型。

2.3 模型转化

参考凸松弛技术，将原始的非凸非线性模型重新表述为一个方便求解的二阶锥规划模型。

用vi,t和iij,t替换上述约束模型中的二次项

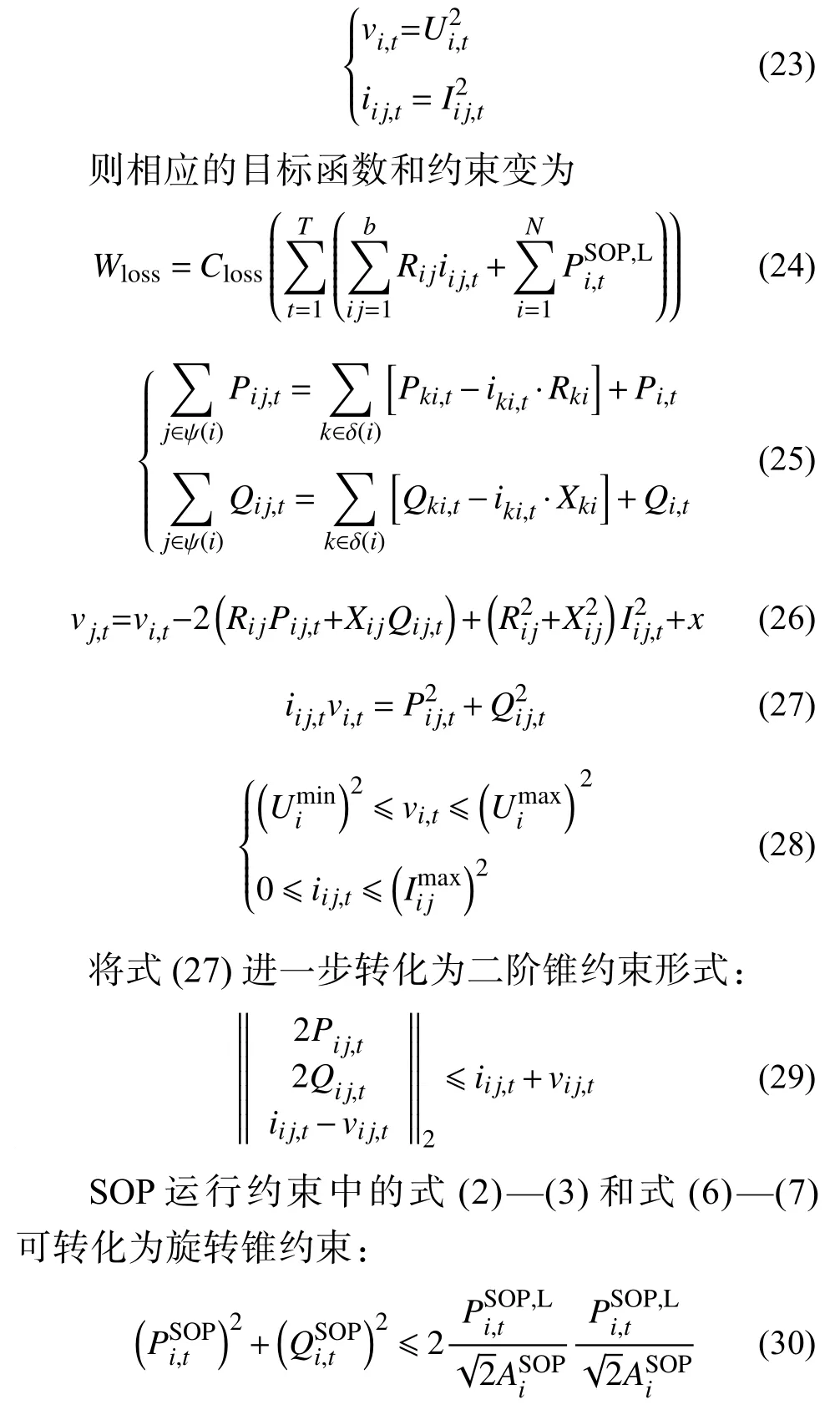
经过上述转化，将原始非线性规划模型转化为二阶锥规划模型(second order cone programming，SOCP)，可调用已有成熟的数学优化工具CPLEX等进行求解。

3 含SOP 的两阶段鲁棒运行模型及求解方法

3.1 两阶段鲁棒优化模型

配电网在实际运行中面临着许多不确定性因素的影响，其预测精度往往难以保证。因此，确定性优化模型得到的方案往往显得过于“冒险”。为避免优化方案过于保守或冒险，本文在优化模型中计及不确定因素，并通过鲁棒调节参数的取值，量化分析决策者风险偏好。

在优化运行的过程中，DG 出力以及用户负荷用电需求存在一定程度上的预测误差，由此建立预测功率与实际功率的关系如下：

本文以最恶劣场景下系统运行经济性最优为目标，则2 阶段鲁棒优化模型可表示为如式(40)所示的矩阵形式：

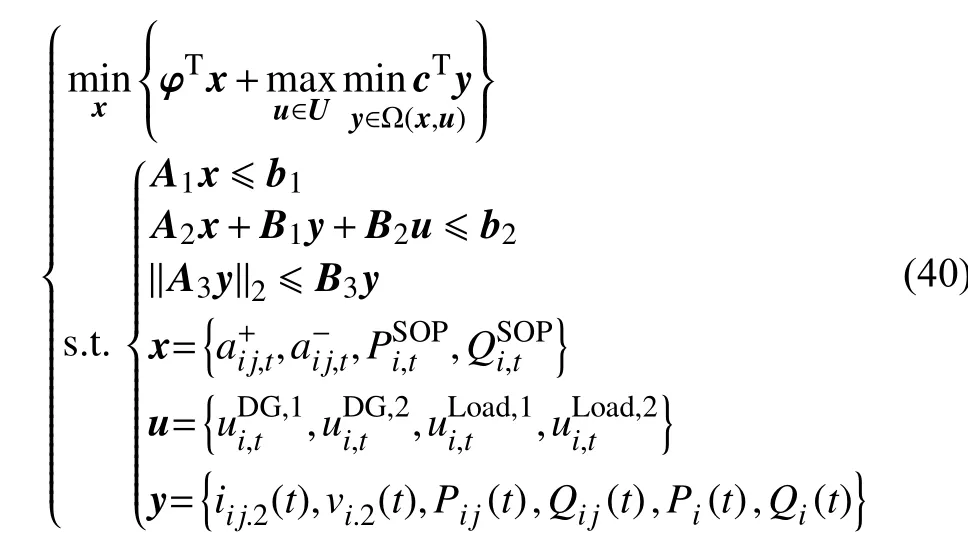
式中：模型最外层的最小化为第1 阶段问题，其优化变量x；内层的最大最小化为第2 阶段问题，优化变量为u和y；A1、A2、A3、B1、B2、B3为相应的系数矩阵；φ、c、b1、b2为系数向量；目标函数对应式(8)、(24)、(38)；第1 行约束对应上文式(4)—(5)、式(34)—(37)；第2 行约束对应式(19)—(22)、式(25)—(28)和(39)，第3 行约束对应式(29)—(33)；第1 阶段是在满足支路潮流以及安全运行等约束的前提下获得优的运行方案；第2 阶段为搜寻运行方案下的最恶劣场景及对应的最小化目标函数。

3.2 求解算法

在优化求解2 阶段鲁棒风险偏好模型时，本文采用列约束生成算法(column-and-constraints generation，C&CG) 将其分解为主子问题，利用主子问题交互迭代的方式求出最优值[16]。其中，主问题即为第1 阶段优化问题，主问题目标函数和约束条件为

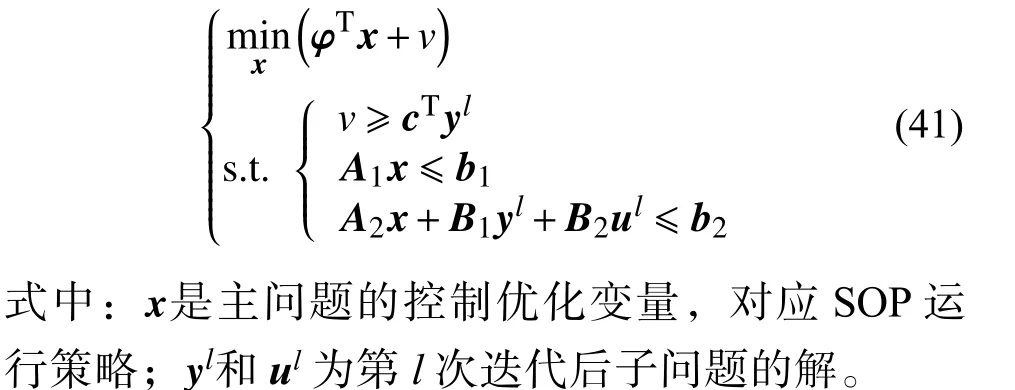
子问题对应上述2 阶段鲁棒优化运行模型的第2 阶段问题，子问题根据主问题中确定的第1阶段优化变量取值和第2 阶段优化变量约束条件，计及不确定集中的最恶劣场景以确定第2 阶段优化变量取值并为模型提供上界，同时生成新的约束条件添加至主问题中继续进行下一轮迭代求解。对于主问题中任意给定的x*，子问题都能够求解出相应最优解Q(x*)。

子问题的目标函数和约束条件为：

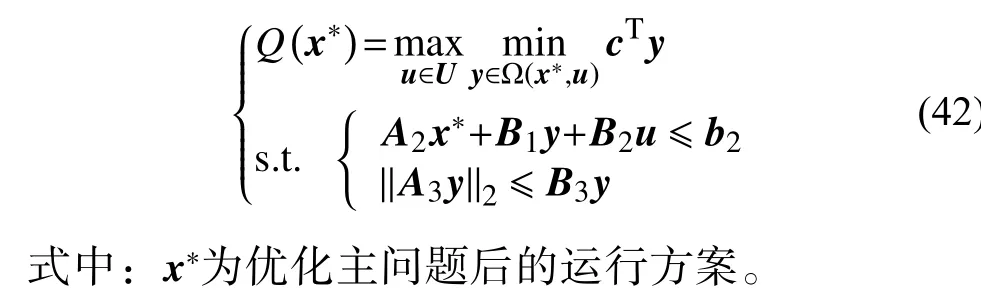
子目标函数为最大最小化问题，是双层优化形式，其表达的含义是在第1 阶段给定的运行方案下搜寻最恶劣的风光荷出力场景及该场景下的最小日运行成本。外层优化max 问题在不确定集合中寻找导致目标函数日运行成本最大的风光荷出力场景即“最恶劣”场景，决策变量为DG 和负荷的波动程度，内层优化min 问题表示在特定的风光荷场景下通过决策变量寻求目标函数最小值，决策变量为系统电压、电流、有功和无功等潮流参数。该问题求解较为困难，可以采用对偶定理，通过引入拉格朗日乘子将其转化为“max”单层优化问题，如下式所示：

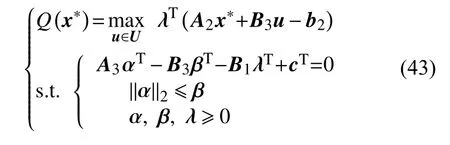
式中：λ、α和β均为拉格朗日乘子。对应的算法步骤为：

1）初始化参数。设置迭代次数k=1；上、下界参数U=+∞，L=–∞；最大迭代次数kmax；收敛精度ε(ε>0)。

4）终止条件判断。若U−L≤ε 成立，计算停止，返回最优解xk和yk。否则，转步骤2），置k=k+1。

C&CG 算法求解鲁棒优化运行模型流程如图3 所示。

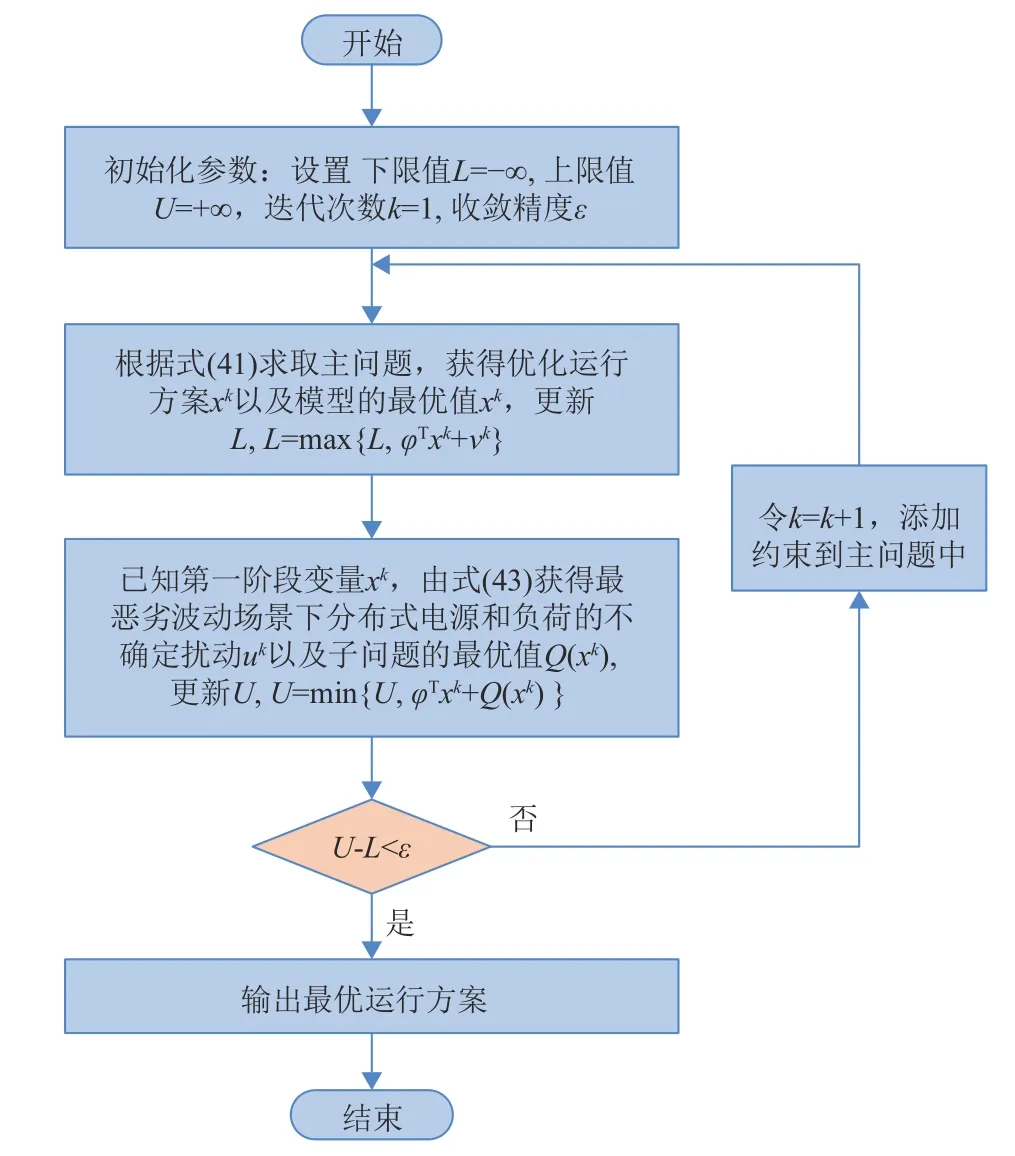
图3 基于C&CG 算法的鲁棒优化运行模型求解流程Fig. 3 The solve loop of robust optimization operation model based on C&CG algorithm

4 算例分析

4.1 算例参数

本文以修改后的IEEE33 节点系统[17]为例进行算例验证，系统结构如图4 所示。其额定电压等级为12.66 kV。系统承受的最大安全电压为1.05（标幺值），最小为0.95（标幺值）。接入DG 的具体参数见表1。所有分布式可再生能源的功率因数都设置为1，即不考虑分布式可再生能源的无功支持[18]。在节点12 和22 之间安装SOP，其中最大容量为0.5 MVA；损耗系数为0.02；向节点注入功率的方向是正方向；网损成本和SOP损耗成本均设为0.57 元/ kW·h[19];总的开关操作次数约束NSB和每个开关最大允许操作次数NB分别取20 次和4 次[20]；开关单次操作费用为7 元/次[21]；不确定性水平ΔPDG和ΔPL均取为10%；ΓDG和ΓLoad取值12。DG 及负荷的功率预测曲线及波动范围如图5 所示。

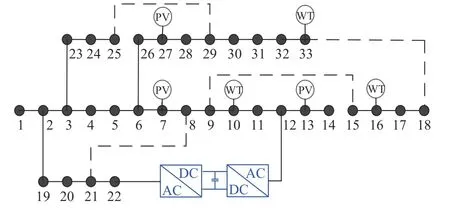
图4 改进的IEEE33 节点配电系统网络结构Fig. 4 The network structure of improved IEEE 33-bus distribution network

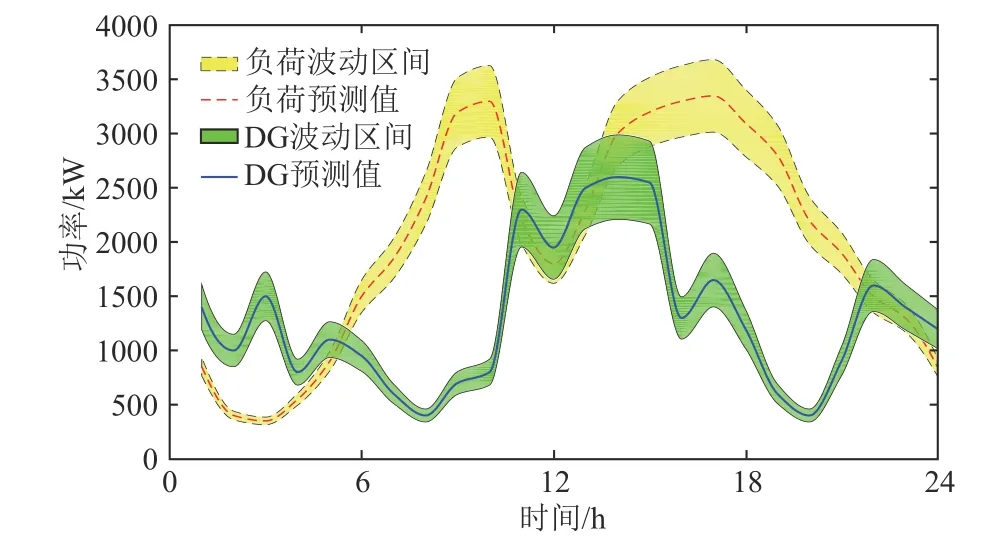
图5 分布式可再生能源和负荷的日运行曲线Fig. 5 Daily operation curves of distributed renewable energy and loads

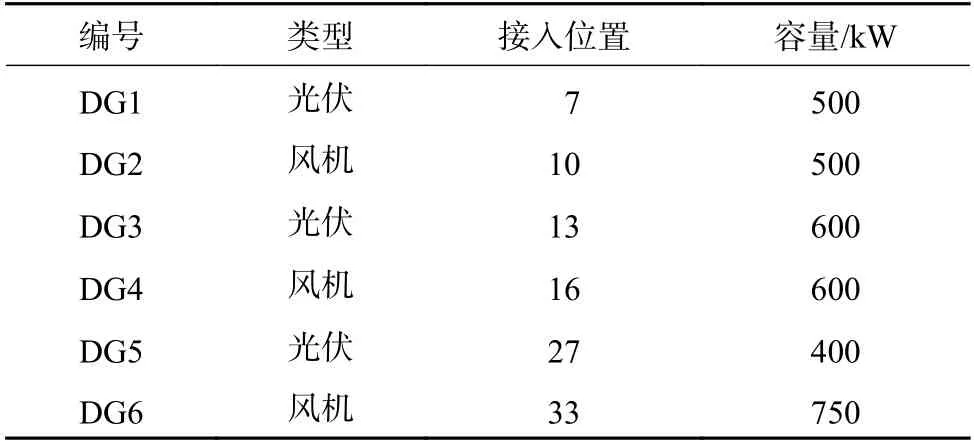
表1 分布式电源参数Table 1 Distributed power supply parameters

4.2 优化结果分析

为了验证所提方案的有效性，本文设计以下3 种方案进行对比，分析各种方案下系统运行成本情况。

方案1：配电网中不考虑联络开关参与优化，仅利用一组SOP 进行配电网运行优化。

方案2：采用本文方法，对联络开关与SOP进行协同优化，但不考虑出力波动性即确定性优化运行方案。

方案3：采用本文方法，对联络开关与SOP协同优化，且用鲁棒优化的方法处理出力波动性即鲁棒优化运行方案。

3 种方案的优化结果如表2 所示。

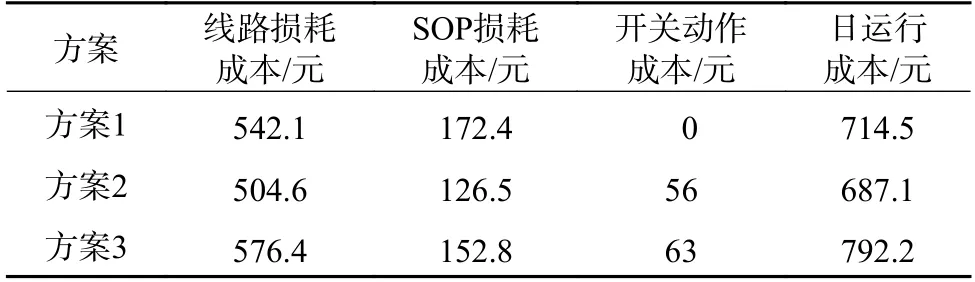
表2 不同方案所得的日运行分析结果Table 2 Results of daily operation analysis by different schemes

通过表2 中方案2 和方案1 的对比可以发现，利用联络开关网络重构和SOP 进行综合优化，相比仅利用SOP 优化，有功网损得到进一步降低，并且SOP 的传输功率有所减小，仅以开关动作成本的牺牲得到总的日运行成本降低，由此可见，网络重构对SOP 的优化结果起到促进作用。对比表2 中方案3 与方案2 的结果可知，为了使得到的优化方案不受DG 出力和负荷需求波动的影响，鲁棒优化模型需要以牺牲一定的经济成本为代价，说明鲁棒动态重构结果具有一定的保守性。因为确定性运行方案忽略DG 和负荷所存在的预测误差，运行在理想环境下，但是显然与实际情况有所出入，现阶段对于DG 以及负荷出力的精准预测很难实现，鲁棒优化方案为了应对DG 出力与负荷波动，考虑了配电网在运行最恶劣的情况下最优，因此网损值逊于确定性方案。

3 种优化方案中SOP 的有功和无功功率输出情况如图6—7 所示。

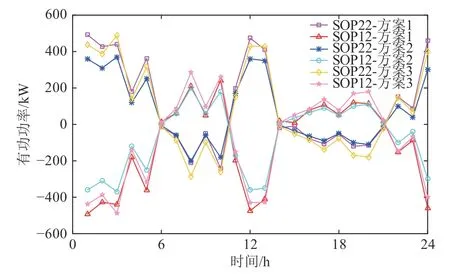
图6 SOP 输出的有功功率Fig. 6 Active power output of SOP

从图6 和图7 中可以看出，SOP 的运行策略与DG 出力与负荷需求密切相关。在6:00—10:00和14:00—21:00 的时间内，DG 的出力小于负荷需求，SOP 将有功功率传输到节点12，以满足系统的功率需求。在11:00—13:00 和22:00—5:00，DG 出力大于负荷需求，SOP 将有功功率反向传输到节点22，以便尽可能地平滑功率波动。在正常运行时SOP 除了提供有功功率外，还提供无功功率的支撑来改善节点电压情况。

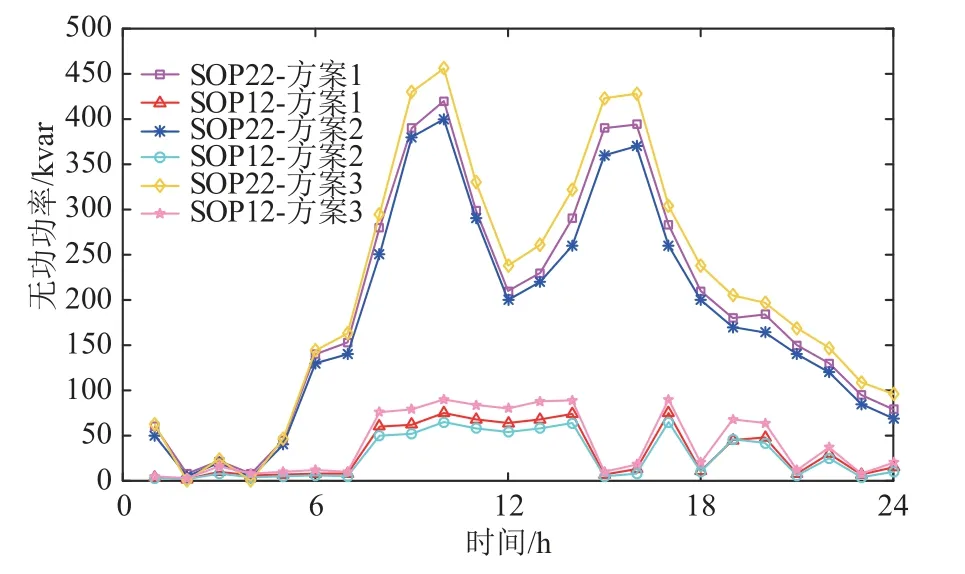
图7 SOP 输出的无功功率Fig. 7 Reactive power output of SOP

为验证本文提出的基于SOP 的鲁棒优化运行方法的有效性，在波动区间内通过蒙特卡罗模拟随机生成的200 个场景，对方案2 的确定性优化和方案3 鲁棒优化进行对比。在模拟过程中，一旦发生违反所需安全运行约束的情况，场景将被标记。表3 总结了不同运行方案的测试结果。

由表3 可知，因为DG 出力与负荷需求的波动性，确定性运行方案在制定时由于没有考虑不确定性的影响，在模拟运行中导致产生大量的越限场景。然而在鲁棒优化运行方案中，只是以微弱的网损牺牲为代价，可将越限情况有效地消除，保证系统安全稳定的运行。

表3 不同方案的蒙特卡洛模拟测试结果Table 3 Monte Carlo simulation test results of different schemes

图8 显示了通过蒙特卡洛模拟生成的200 个场景中的不同运行方案在一天中所能获得的每个时刻的最大和最小电压。

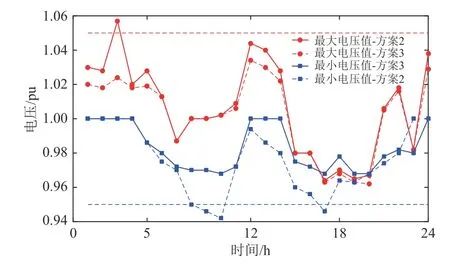
图8 系统最大和最小电压幅值Fig. 8 Maximum and minimum voltage amplitude of the system

通过图8 可知，与确定性运行方案相比，通过SOP 的鲁棒调节可将节点电压保持在所需范围内，有效解决了由于DG 出力与负荷需求的波动造成的电压越限问题。

4.3 鲁棒调节参数和预测误差对结果的影响分析

为探究鲁棒性调节参数和预测误差对运行结果的影响，设置风光出力和负荷随机的鲁棒调节参数分别为0、6、12、18、24，波动预测误差分别为10%、20%、30%，几种不同参数下的优化结果如表4 所示。

从表4 中可以看出，在相同的DG 与负荷预测误差下，随着鲁棒调节参数的增加，鲁棒性逐渐增加，可以应对更多的不确定性的影响，但因为考虑的是最差场景的运行环境，会使运行总成本增加。特别地，当鲁棒调节参数取值为0 时，鲁棒优化问题变为确定性优化问题，DG 与负荷预测误差的改变，对运行总成本不会产生影响；在相同的鲁棒参数下，随着DG 与负荷预测误差增大时，为应对DG 出力波动可能发生的最坏扰动，导致系统运行总成本也增大。

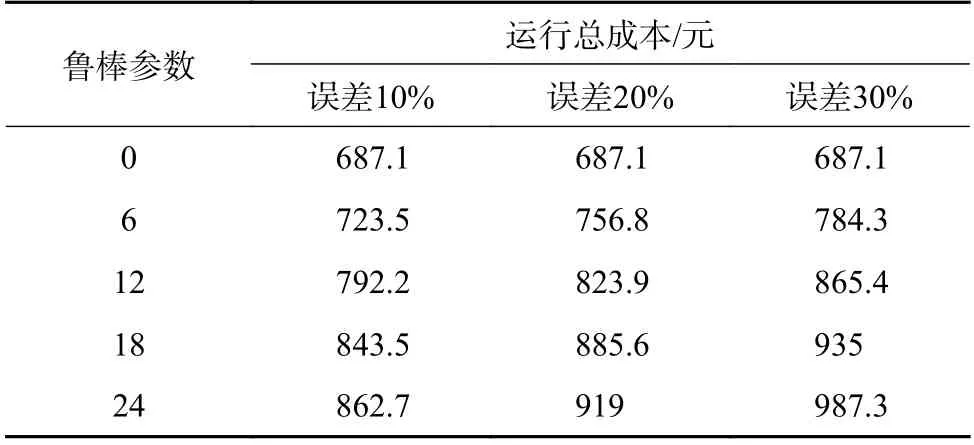
表4 不同鲁棒调节参数和预测误差下的运行总成本Table 4 Total operating cost under different robust regulationparameters and forecast errors

因此，在实际应用中，决策者可以根据实际需要，灵活、适当地选取鲁棒调节参数的大小，以满足系统经济性和鲁棒性的协调关系，既要体现其经济效益，又能减少运行风险，满足系统安全性需要。

5 结论

为应对配电网中分布式电源与负荷的随机性与波动性给配电网运行带来的挑战，本文提出了一种基于SOP 的主动配电网两阶段鲁棒优化方法。通过算例分析结果表明：

1）所提出的模型考虑了DG 出力和负荷需求的不确定性，通过利用主子问题交互迭代的方法求解，配电网能够得到“最恶劣”场景下系统运行成本最小的运行方案。且通过改变鲁棒调节参数，能够灵活调整配电网运行方案的保守性，有利于配电网决策者在经济成本和运行风险间进行合理选择。

2）与确定性优化方法进行了对比，鲁棒优化运行方案仅以较小的运行成本代价，极大减少了系统电压越限情况，使系统更加安全稳定的运行。