基于迭代软阈值压缩感知理论的直流输电双极短路故障测距方法
2021-12-20王振浩董人铭成龙李国庆王朝斌
王振浩,董人铭,成龙,李国庆,王朝斌
(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林省吉林市 132012)
0 引言
近些年来,输电技术随着用电能力和传输能力的发展不断进步。基于模块化多电平换流器的高压直流输电技术(modular multilevel converterhigh voltage direct current transmission, MMC-HVDC)具有传送容量大、故障修复时间短、对器件开关一致性要求低等优势而越来越多地被用于构建大规模直流系统[1-2]。
高压直流输电距离长、跨越地区的地形地貌复杂、气候差别大,导致系统的故障率较高。针对目前我国的特高压交直流混联大电网运行形态,直流系统故障或长时间停运会导致严重的输送功率缺失,对电网的安全稳定运行有较大隐患。在不同种类直流输电线路故障模式中,双极短路故障的危害是最大的,所以快速准确地对直流输电线路双极短路故障进行故障定位极其重要。
目前直流输电故障定位方法以行波法为主。行波法是根据波头到达单端或双端的时刻与行波传播速度之间的关系计算故障距离[3-5]。故行波法的主要技术难点为行波波头的捕获、行波波速的确定以及双端行波法中2 端时钟同步的问题。
行波波头的捕获现阶段多用小波变换对行波波形进行突变点分析,且能较好地消除系统干扰。尤其是基于小波模极大值理论的波头标定方法对故障行波波头标定更加准确[6]。文献[7]提出利用小波包和相关算法相结合的方法来实现确定第二个行波波头的性质,进而实现单端故障测距;文献[8]提出基于数学形态学的多尺度数学形态滤波器,提高故障行波波形突变点识别的准确性。考虑到行波波速的影响,在不同介质中,行波波速的差异较大,同时行波在传播的过程中波速也会随频率的衰减而发生变化。文献[9]通过将实际仿真得到的模拟曲线与数学公式相结合描述了行波波速随频率变化而变化的关系曲线。但对于不同的实际系统曲线会发生变化,不具有普遍性,且测距过程繁琐。文献[10]通过单端测距方法,检测每个行波到达测量端的时间,利用多个行波波头到达的时间关系计算出故障点,可以避免行波波速的影响,但此方法需要对多个行波波头进行准确检测,实际工程的难度较大。文献[11]基于行波高频量的衰减特性进行故障测距,且提出单端、双端2 种方法,单端法难以检测暂态信号高频分量,双端法当故障位置处于线路中点附近时,误差较大。由于架空线-电缆混合线路存在阻抗不连续点,会造成行波的多次折反射以及波速变化等问题,进一步加大行波法故障定位的难度。由于时钟同步问题,是采用双端法故障测距时不可回避的难点,现阶段时钟同步主要是由GPS 系统共享时钟公共信号完成,同步误差可以控制在0.1 μs 以内[12]。
基于以上分析,目前行波法主要问题集中存在于波头的识别以及行波波速的确定。本文针对双极短路提出基于迭代软阈值压缩感知理论的直流输电双极短路故障测距方法,有效地规避了行波法存在的问题,在实际仿真分析中有较高的精度,同时测距方法简洁,适用范围广,对于线路参数只需考虑线路的阻抗,所以在架空线路、电缆线路、复杂输电线路中均可应用。
由于直流输电线路中单极故障、断线故障没有明显的故障特征[13],难以精确提取高频分量。双极短路故障又是直流输电系统中最严重的故障,且以永久性故障为主,因此本文只针对双极短路故障。
1 MMC-HVDC 输电线路故障分析
1.1 MMC 等效模型
MMC-HVDC 是由换流站和输电线路组成,其中换流站包括整流侧换流站和逆变侧换流站。MMC 的拓扑结构如图1 所示。换流器由三相六个桥臂组成,每一相的上、下桥臂各有N个子模块和一个桥臂电抗器Larm。其中,子模块是通过投切来拟合逼近正弦波,正常运行时,每一相同一时刻上、下桥臂投入的子模块数量之和均为N,来维持母线电压的恒定;桥臂电抗器在直流侧发生短路时可以抑制短路电流的上升速度。
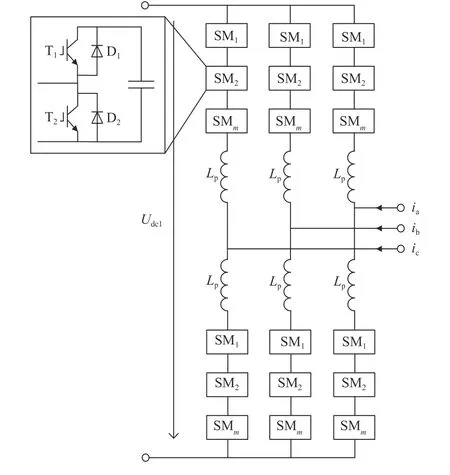
图1 MMC 拓扑结构Fig. 1 Topological structure of modular multilevel converter
MMC 子模块有闭锁、投入、切除3 个状态,当系统处于稳态正常运行时,直流输出电流在三相中平均分配,交流输出电流在上下桥臂中平均分配,每相都有N个子模块处于投入状态。
当MMC 发生双极短路时,短时间内MMC子模块会闭锁,本文研究的数据信息需要在子模块闭锁前提取,本节只分析从发生故障瞬间到MMC 子模块闭锁前的暂态过程。发生故障后,直流线路注入的短路电流由2 部分组成,分别是子模块的电容放电电流和交流侧馈入的短路电流。交流侧馈入的短路电流与电容放电电流相比极小,对于双极短路分析可以将交流系统忽略。
由于MMC 中包含闭环控制和大量非线性过程,对其进行短路特性分析极其复杂,故本文只考虑子模块脉冲闭锁保护,不考虑改变MMC 运行方式的保护以及断路器对MMC 的保护,同时忽略MMC 中半导体元器件的导通电阻压降。由于时钟同步技术的成熟,本文不考虑多个测量装置之间的同步误差以及相关通信过程。
1.2 双极短路暂态分析与等效电路
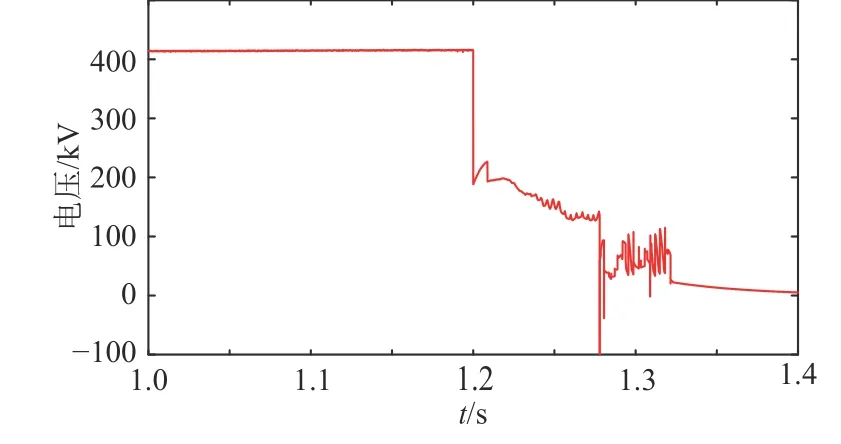
当直流输电线路上某点在0.85 s 发生双极短路故障时,故障点处电压、电流仿真波形如图2、图3 所示。
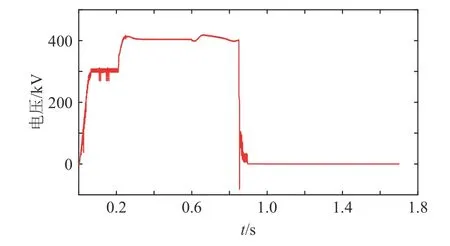
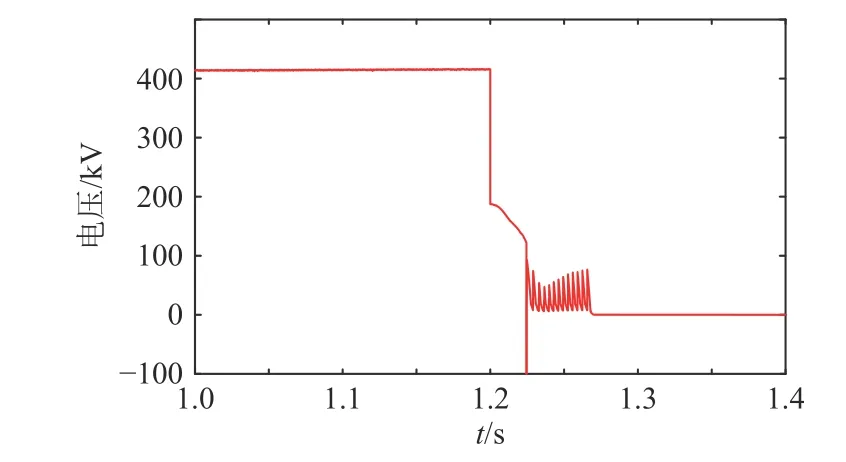
图2 故障点处电压仿真波形Fig. 2 Simulation waveform of voltage at fault point
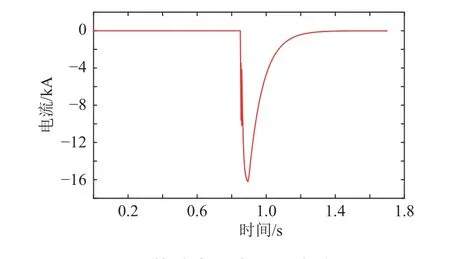
图3 故障点处电流仿真波形Fig. 3 Simulation waveform of current at fault point
由图2 可知,当直流系统输电线路发生双极短路时,故障点电压由额定电压迅速跌落,经振荡过程后衰减为零,故障电压跌落过程近似于阶跃函数。
对于故障电流,设由地到故障点的方向为电流的正方向,由图3 可知故障电流由零迅速增大,增大到最大值之后较为缓慢地衰减为零。故障电流的增大过程也类似于阶跃函数。
对电压降落波形做离散傅里叶变换,可得到电压波形的频率特性,如图4 所示。可看出低频分量的幅值较高,高频分量的幅值很小,这也符合阶跃函数的频率特性。
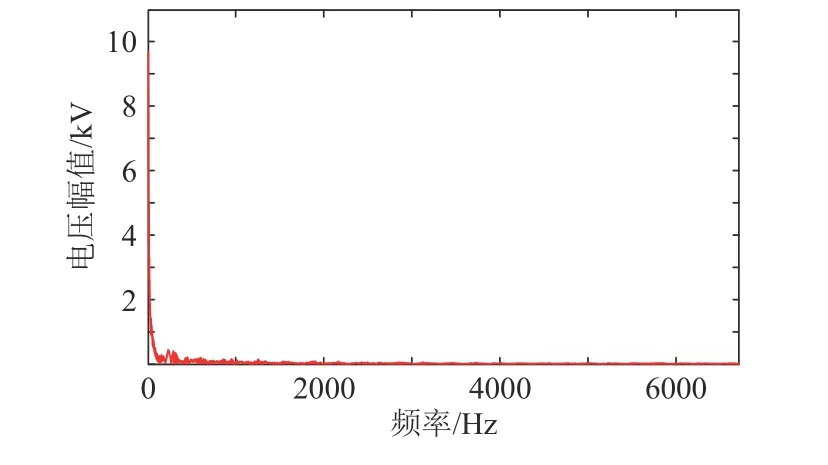
图4 故障电压频谱Fig. 4 Fault voltage spectrum
当直流输电系统发生双极短路时,短路电流的流通路径如图5 所示。此时MMC 直流侧故障电流通过正极线路、三相上桥臂MMC 子模块、三相下桥臂MMC 子模块、负极线路、两组桥臂电抗以及故障同类形成闭合回路。其中Larm为MMC 桥臂等效电感。
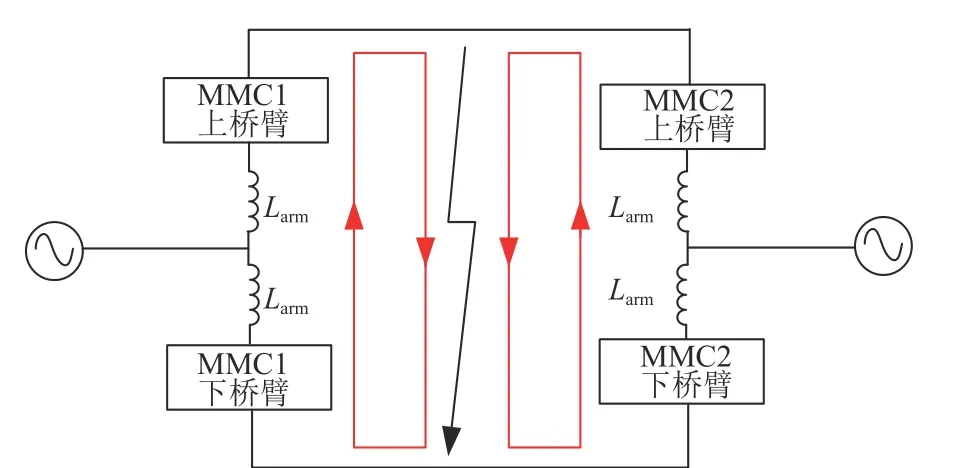
图5 系统双极短路电流流通路径Fig. 5 System bipolar short circuit current flow path
对于MMC 模块,若忽略交流侧的等效阻抗,则MMC 可以等效为LC 串联电路,其等效电路图如图6 所示。
图6 中Lf、Cf分别为双极短路故障后,MMC子模块闭锁前等效电路的电感、电容,其值如式(1)所示。
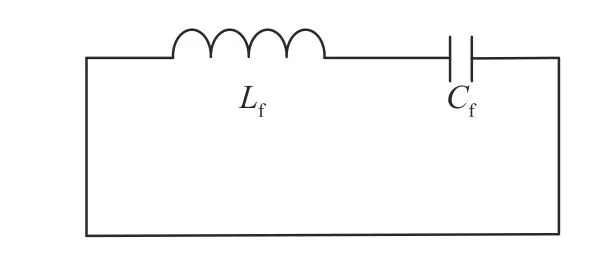
图6 MMC 等效电路图Fig. 6 Equivalent circuit of MMC

式中:N为MMC 单相子模块个数;Lp为桥臂电抗;C0为MMC 桥臂子模块电容。
经过上述分析,MMC 和输电线路的阻抗简化模型的数学表达式如式(2)(3)所示:

2 故障电压波形高频分量提取
在直流侧注入不同频率的谐波来测量MMC的等值阻抗,可得到当谐波频率大于2700 Hz 后,实际测量值与理论计算值几乎完全吻合[14],本文提取的高频分量在3500 Hz 附近。
目前信号高频分量提取大多使用傅里叶变换[15]、小波变换[16]、希尔伯特-黄变换(Hilbert-Huang Transform,HHT)[17]等。但是傅里叶变换只能在平稳信号中应用,对于非平稳非周期信号只能分解出每个高频分量的幅值,无法与瞬间时刻相对应[18];根据测不准原理,小波变换在高频处频率分辨率较低,小波变换的分辨率无法满足本文高频分量提取的精度要求;HHT 变换容易造成模态混叠,影响提取精度。
近年,由Daubechies 等人提出的同步挤压小波变换(Synchrosqueezing Wavelet Transform,SWT)是在小波变换的基础上,通过在频率方向压缩小波变换的时频图得到的,此变换有效避免了上述方法产生的问题,对于高频分量的提取有较高的精度[19]。
实际的非平稳非周期信号可以表示成多个分量求和的形式。
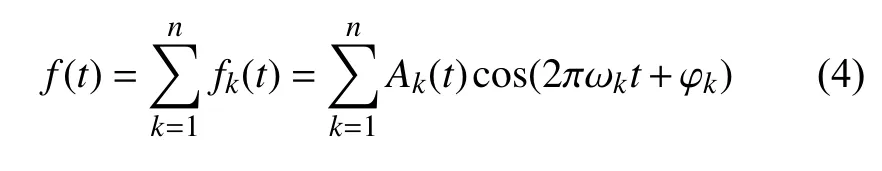

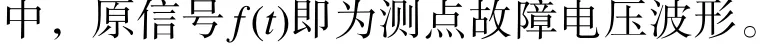
3 基于虚拟节点电流求解的故障定位方法
输电线路模型为900 km 长的线路,预设精度为300 m,则可以将输电线路用3001 个“虚拟节点”将输电线路分成3000 块,其中线路两侧的MMC 各单独分成一块。
当输电线路某点发生双极短路故障时,相当于在故障点产生一个对地电流,非故障点的对地电流为零。若某一“虚拟节点”恰好发生双极短路故障,则此“虚拟节点”的对地电流非零,其他“虚拟节点”对地电流为零;若某两个“虚拟节点”之间发生双极短路故障,则此故障电流可以等效为两侧“虚拟节点”的对地电流[14],故障点可以近似认为是两侧“虚拟节点”中对地电流较大的点。
3.1 MMC-HVDC 节点电压方程
对于含有n个“虚拟节点”的输电线路,可列节点电压方程如式(11),其中矩阵Yn×n(ω)为节点高频导纳矩阵。当系统正常运行时,高频电流向量In×1(ω)为零向量,即没有节点有对地电流。若假设节点l为故障点,则高频电流向量In×1(ω)中只有I˙l(ω)元素为非零值。若故障发生在2 个节点之间,则只有这2 个节点的电流值为非零值。
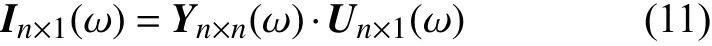
在本文的故障测距方法中,电流向量In×1为待求量,电压向量Un×1为已知的实测量。式(11)可写为式(12)。
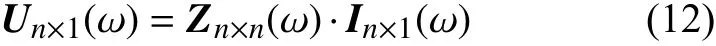
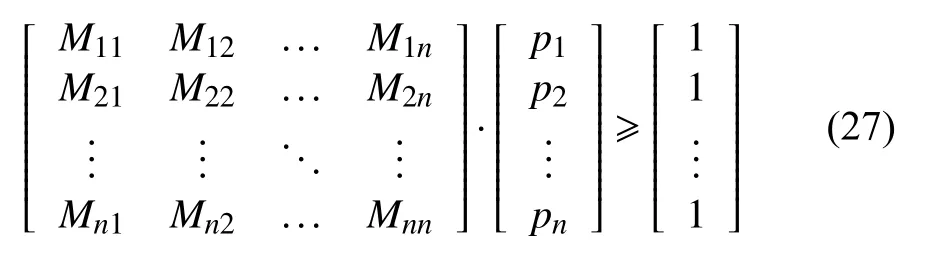
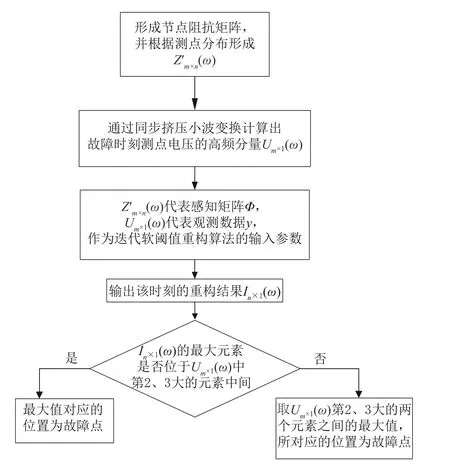
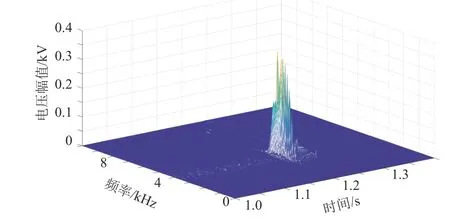
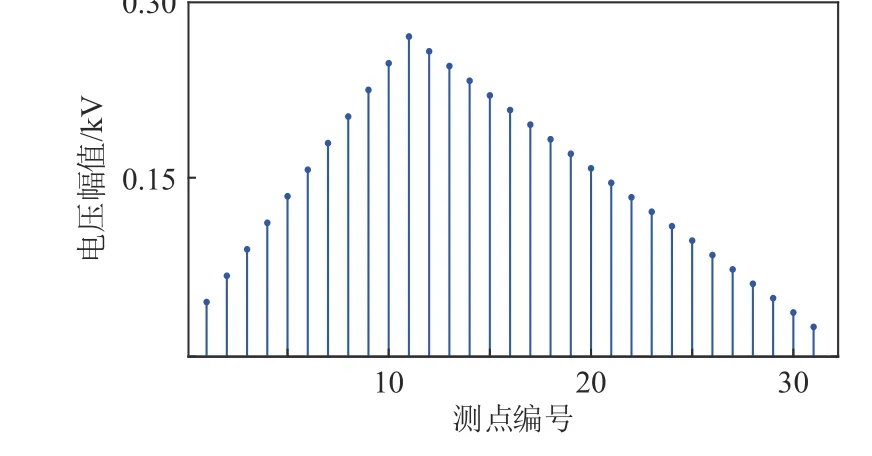
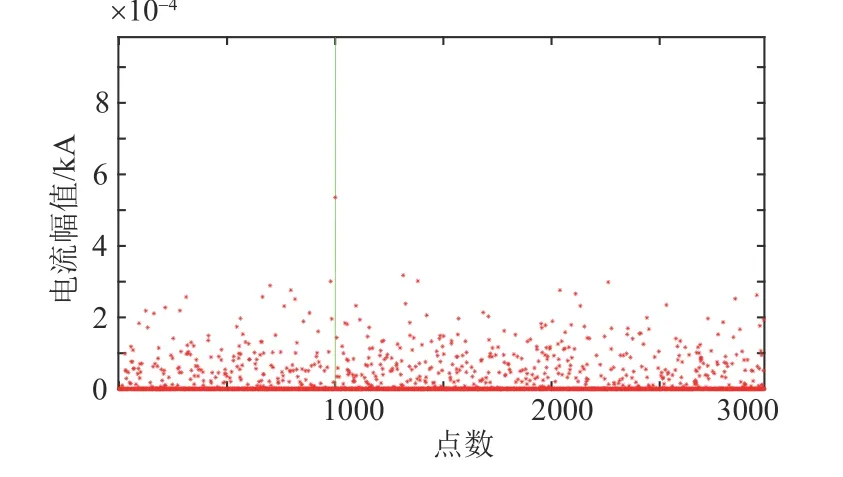
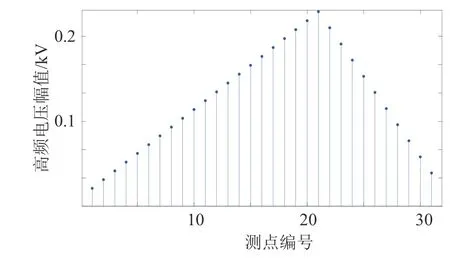
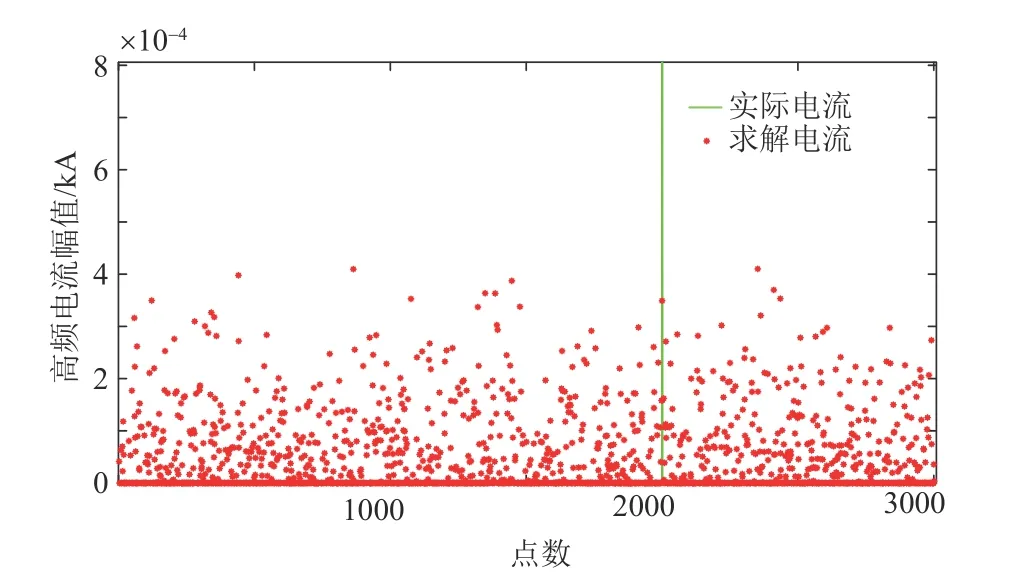
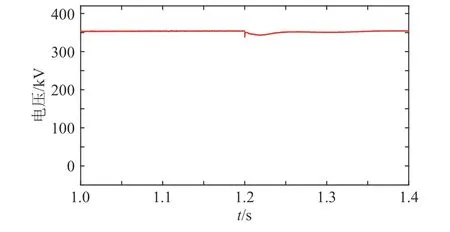
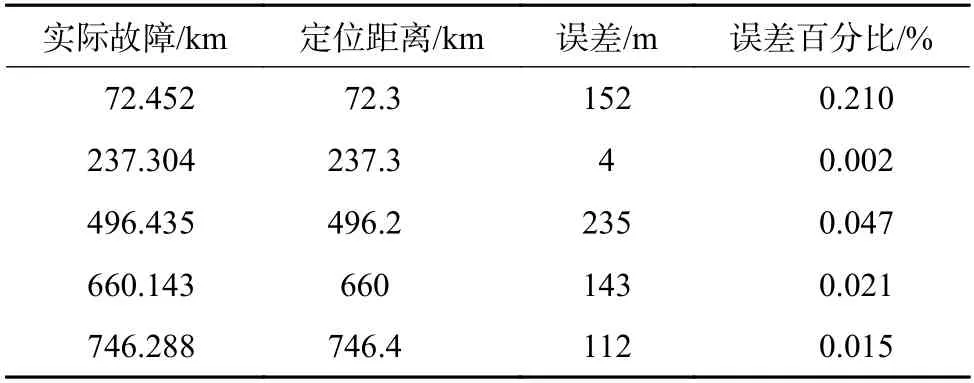
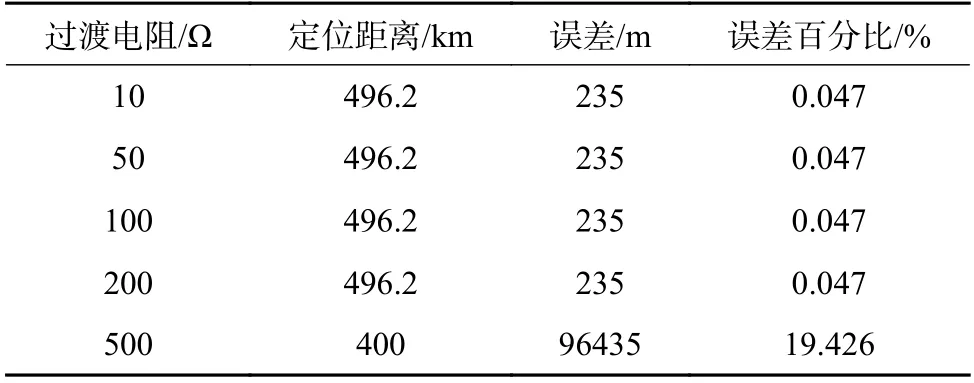
当对地电压测量装置只安装在m(m< 压缩感知理论广泛应用于信号处理、图像处理等领域,对于具有稀疏性的信号可以精确重构,而且突破了香农理论,对待重构信号的采样频率要求较低[20]。 压缩感知的数学模型可被描述为式(16)范数正则化公式来寻找最优解,即转化为式(19)的优化问题。 式中:q为 待重构信号的稀疏度;p为待重构信号的长度。 对应于本文,稀疏度q取2;信号长度p取3001,进而求得测点数量应不少于22 个。由于线路中“虚拟节点”之间的距离很近,导致计算2点间故障时的电气数值特征差异不明显。如果将每个节点都假设为故障点,若2 个节点相邻,那么任意节点发生故障导致电压暂降都能被相邻节点检测到(Mi j=1),若2 个节点不相邻,那么任意节点发生故障导致电压暂降都不能被另一个节点检测到(Mi j=0),另外,任意节点i发生故障电压暂降都能被本身检测到(Mii=1)。 根据以上分析,有 可以看出观测矩阵M是一个n维的二进制方阵。建立完可观测矩阵后,需要对观测点的位置选择进行配置。对于n节 点的网络,定义n维状态向量P,对于其中的任一元素pi,有目标函数:使得总测点数最少 式中:p(i)的数值表示节点i是否为测点,若p(i)=0则节点i不是测点;若p(i)=1则节点i是测点。 约束条件: 此模型称为0−1 规划优化方法的基于可观测区域的布点优化模型。 由于本测距方法所建立的节点数较多,所以会出现通过0−1 规划优化过程第一次求解出的测点数m与 本文实际规定的测点数n相 比,会有m>n,为进一步降低测点冗余度以降低测距成本,需要对第一次布点优化的结果进行多次0−l 规划优化。 在第2 次0−1 规划优化中,将前一次优化后的目标函数测点数量m及位置更新作为下一次目标函数优化对应的初始节点数量及位置,直到第K次优化模型求解测点数m≤n时停止,测点分布位置取第K-1 次求解的结果。 结合本测距方法和相应的参数,经过4 次求解得到测量装置安装点应该为第294、385、476、···、2715、2842 个“虚拟节点”处,测点数量为29 个,第5 次0−1 规划优化结果测点数为9 个,小于测点数量的下限值,因此应当取第4 次求解的测点数量及位置分布。同时可以发现测点分布位置是近似均匀分布的,但是由于线路两端换流站的等效阻抗与线路的等效阻抗相比,有较大差别,所以为使得测量结果更加精确,在得到测点分布的结果之后还应该在两个换流站的出口、入口与架空线路之间即第1 和3001 个“虚拟节点”处再各加一个测点。因此最终测点总数为31 个,符合本文压缩感知算法对测点数量最小值的约束。 根据前述分析本文所述的故障测距方法可大致分为3 步: 1)根据含有“虚拟节点”的直流输电网形成高频节点阻抗矩阵,并将其正则化处理,得到感知矩阵Z′m×n(ω); 2)在故障发生后,MMC 子模块闭锁前收集所有测点的故障电压波形,进行同步挤压小波变换,得到每个测点信号在故障时刻所对应的高频分量幅值,得到测点电压向量,再乘以变换矩阵得到向量Um×1(ω); 3)将前两个步骤得到的阻抗矩阵和测量电压,导入到基于迭代软阈值的压缩感知算法中,重构出电流向量In×1(ω)。 需要注意的是,由于上述步骤所用的算法中,存在难以避免的误差,这会导致电流向量In×1(ω)除了故障点的对地电流值为非零以外,仍存在大量对地电流值为非零的点。但是一般来说故障点处的对地电流值是最大值。故选取电流向量In×1(ω)中的最大值所对应的“虚拟节点”为故障点。 故障测距流程如图7 所示。 图7 故障测距流程图Fig. 7 Flowchart of fault location 为验证上述故障测距方法的有效性,在PSCAD/EMTDC 中搭建两端直流输电系统,进行故障定位仿真。直流系统MMC 换流站参数设计如表1 所示,输电线路相关参数设计如表2所示。 表1 MMC 换流站参数Table 1 Parameters of MMC converter station 表2 输电线路参数Table 2 Parameters of transmission line 本文输电线路故障测距预设精度为300 m;共设置3001 个“虚拟节点”,对地电压测量装置共有31 个。仿真采样步长为50 μs,故障发生时刻为1.2 s,系统运行持续时间为1.7 s。 当直流输电系统在“虚拟节点”处发生双极短路故障时,假设故障位置为300 km(位置1)处,则图8 为某一测点测得的故障电压波形。在本文方法中,只需提取故障波形在故障发生瞬间时刻的信息,但为体现出故障电压的变化过程,波形图显示的持续时间设置为从1 s 时刻开始到发生故障后达到新稳态1.4 s 时刻为止。对此波形进行滤波,范围为3000~4000 Hz,再对滤波后的波形进行同步挤压小波变换,得到其时频三维图像如图9 所示。 图8 位置1 故障时测点故障电压波形图Fig. 8 Waveform diagram of fault voltage at measuring point when fault occurred at position 1 图9 测点故障电压三维时频图Fig. 9 Three-dimensional time-frequency diagram of fault voltage at measuring point 提取每个测点在故障发生时刻的电压高频分量,高频分量幅值变化如图10 所示。再将此信息形成的测点电压向量和输电系统节点阻抗矩阵进行变换,送入压缩感知算法中,得到电流向量In×1(ω),并与实际的节点故障电流做对比,结果如图11 所示,可以发现,故障定位在300 km 处,结果十分精确,此时故障定位误差值为零。如果故障位置离“虚拟节点”很近时,定位误差也极小。 图10 位置1 故障测点高频分量幅值图Fig. 10 High-frequency component amplitude of fault measuring point at position 1 图11 位置1 处故障时稀疏信号求解图Fig. 11 Diagram of sparse signal solution when fault occurred at position 1 当双极短路故障发生在非“虚拟节点”上时,假设故障发生在2 个“虚拟节点”的中点600.150 km(位置2)处时,所有测点的故障电压高频分量值变化如图12 所示。 图12 位置2 故障测点高频分量幅值图Fig. 12 High-frequency component amplitude of fault measuring point at position 2 将此数据带入压缩感知算法中,可得计算出的故障位置与实际位置对比如图13 所示。可以看出压缩感知算法求解出的电流向量In×1(ω)的最大值并不是故障点,即故障点所对应的解并不是全局最优解。但是由图12 可知,故障点一定位于第19 和第21 个测量点之间,即位于两个测点所对应的“虚拟节点”之间,故只需要在此范围寻找局部最优解即可。局部对比图如图14 所示。不难看出,故障点定位在第2000 个“虚拟节点”上,即故障位置为600 km,故障测距误差为150 m。 图13 位置2 故障稀疏信号求解图Fig. 13 Diagram of sparse signal solution when fault occurred at position 2 当短路点接有10 Ω 过渡电阻时,测点测得的故障电压波形如图15 所示。可以看出与金属接地故障相比,短路点通过过渡电阻接地时测点测得的故障暂降电压衰减到稳态的振荡过程更长。 图15 10 Ω 过渡电阻测点故障电压分析图Fig. 15 Analysis diagram of fault voltage at measuring point under transition resistance of 10 Ω 由于故障瞬间电压暂降部分并未受到影响,故一定范围内的过渡电阻并不影响故障测距精度。随着过渡电阻的增大,故障电压的阶跃下降效果随之减弱,如图16 所示为500 Ω 过渡电阻故障电压波形图,因此过大的过渡电阻会导致本方法的测距失效。 图16 500 Ω 过渡电阻测点故障电压分析图Fig. 16 Analysis diagram of fault voltage at measuring point under transition resistance of 500 Ω 在输电线路中随机生成5 个故障位置,并对其进行故障测距,结果如表3 所示。 表3 故障测距结果Table 3 Fault location results 在496.335 km 处分别加入10 Ω、50 Ω、100 Ω、200 Ω、500 Ω 的过渡电阻,故障测距结果如表4。 表4 496.435 km 处不同过渡电阻测距结果Table 4 Fault location results under different transition resistances at the position of 496.335 km 本文提出的基于迭代软阈值压缩感知理论的直流输电双极短路故障测距方法的优点如下: 1)实现了双极短路故障定位,无需考虑波速、行波波头等难以准确计量的因素,且结果具有稳定性; 2)故障位置离“虚拟节点”越近,精度越高,且所有的相关参数和信息都容易获得,信息量少,对通信过程的要求较低; 3)随着对地电压测量装置成本的降低,可以增加“虚拟节点”的数量,使得“虚拟节点”之间的距离可以进一步缩小,提高故障定位精度。由于测点的分布数量随“虚拟节点”数量的增多,非线性增长,所以当精度有大范围提高或线路长度继续增加时,其成本不会大规模提升,有较好的经济性。 4)本方法适用线路范围广且耐受过渡电阻能力较好。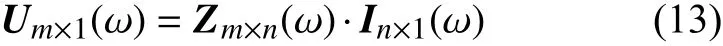
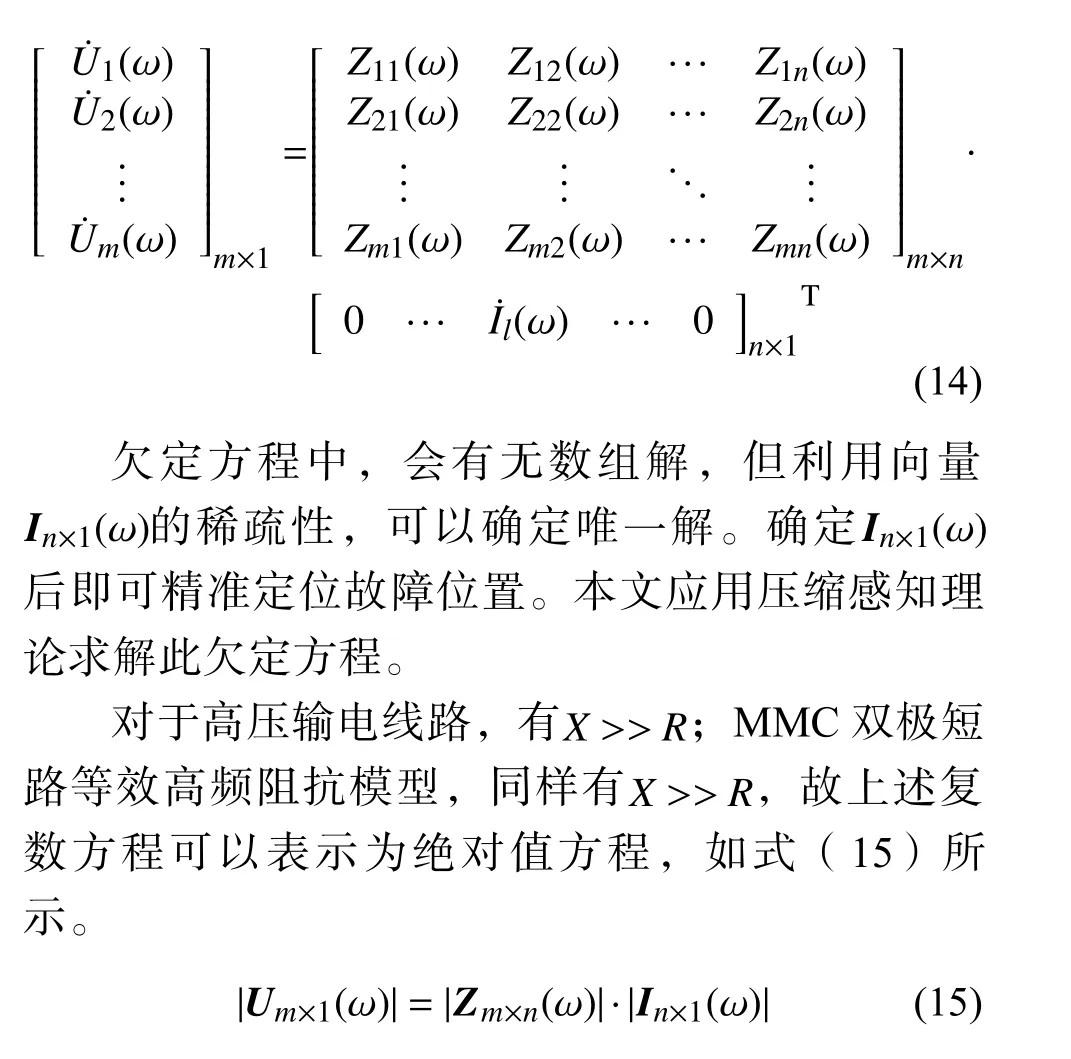
3.2 基于迭代软阈值的压缩感知理论


3.3 输电线路测点分布设计


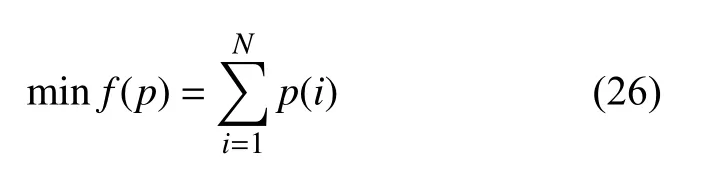
3.4 故障定位方法流程
4 仿真验证与分析


5 结论
