基于层次分析法和云模型的风电场运行性能多维评价模型

2021-12-20罗春辉瞿纲举邹同华汤涛谢佳罗茜

现代电力 2021年6期

罗春辉，瞿纲举，邹同华，汤涛，谢佳，罗茜

（1. 湖南省送变电工程有限公司，湖南省长沙市 410015；2. 智能电网运行与控制湖南省重点实验室(长沙理工大学)，湖南省长沙市 410114）

0 引言

随着我国风电渗透率逐年提高，风力发电的不稳定性和间歇性对电网安全稳定经济运行的影响更加凸显。在国家扶持风力发电快速发展的背景下，保证电力系统安全稳定的基础上降低发电成本，促进清洁能源消纳已成为当务之急[1-3]。通过分析利用大量风电并网运行数据可有效指导风电场生产运行，进而为高风电渗透率场景下电网安全经济运行提供重要保障[4-7]，因此，有必要对风电场运行状态的分析和评价方法进行深入研究。

目前，对于风电场运行性能的评价可以分为评价指标研究和评估方法研究两类。文献[8-12]从多个角度构建了风电场评价指标，丰富了风电统计指标体系，但因应用场景不同，未能实现对风电场实际生产运行情况的综合反映。在构建评估指标的基础上，对于风电场评估方法的研究主要可以归纳为两类：统计分析[13-16]和综合评估[17-19]。其中统计分析方法是对数据进行定量处理的理论和方法，一般是指对统计数据进行收集、分类并进行解释的过程。综合评估方法也称为多指标综合评估方法，是指同时评估多个指标和多个单位，并对评估目标进行整体定量判断的方法。文献[13]根据风电场的出力数据，运用统计分析方法对东北区域风电出力同时率、概率分布、负荷相关性等特性指标进行分析。文献[14]将风电场的特性评价指标分为风电自然特性和与电网交互作用特性两大类，从多个角度综合反映了风电的统计规律。文献[15]提出一种考虑风电机组可靠性与风速相关性的风电场可靠性评估方法，考虑风速与风电机组故障率之间的相关性，评估风速对风电场可靠性的影响。文献[16]通过分析海上风电场各种拓扑结构的可靠性和经济性，利用可靠性框图对链式风电场的可靠性进行了分析，采用分类方法对环型风电场的可靠性进行了分析。文献[13-16]得到的只是一些不确定的关系，结论局限于在统计和概率分布层面对风电场的运行性能进行分析，并未将各个方面的影响因素进行综合，缺乏整体性评价。文献[17]基于变权灰云模型完成了风电场并网技术性能的综合评价，通过不同风电场并网性能之间的对比，验证了方法的有效性。文献[18]利用逼近理想解排序法（technique for order preference by similarity to an ideal solution，TOPSIS）实现了风电场的综合评价排名，但评价指标以风电场的电能质量、并网指标为主，与文献[17]同样未考虑风电场生产中较为重要的电量指标。文献[19]根据层次分析法评价风电场运行的经济性，但评价指标采用评分的方法，主观性较强，不能反映风电场的实际运行情况。

由上述分析可知，目前对于风电场运行性能的评价方法以统计分析方法为主，通过对相关运行数据以图表的形式进行整理、解释，但对风电场运行性能进行综合评价方面的研究较少，且侧重于通过风电场的单一性指标来反映整体的运行性能，未考虑直接反映风电场生产经济效益的电量因素。风电场在实际生产过程中涉及的影响因素、运行指标较多，需要将风电场运行的多个指标进行综合分析，以便找出影响风电场生产运行水平的相关因素，从而提高风电场的经济效益，促进风电消纳。

本文将风电场运行性能作为一个整体进行分解，充分体现评价的层次性、各指标间的关联关系及对整体评价的影响程度。把运行性能状态作为一个定性概念，运用正态云模型表示此概念的不确定性。通过权重向量和模糊关系模型进行模糊运算，从而得到风电场运行性能的综合评价结果。最后，以国内某风电场的实际运行数据为算例分析，对比验证了本文风电场运行特性评价方法的合理性和有效性。

1 构建评价指标体系

1.1 运行性能评价指标构建

风电场运行指标包括电量指标、设备运行指标、运行维护指标以及电力消耗指标，对于风电场的运行评价应包括设备运行评价、生产维护评价、电力消耗评价以及发电量评价等4 个方面[20]。根据层次分析法（analytic hierarchy process，AHP）的基本思想，目标层通常只有一个要素，并对设计要素进行评价，本文中即是风电场的运行性能。对于准则层，参照标准NB/T 31045—2013 《风电场运行指标与评价导则》，建立风电场运行性能评估的准则层包含设备运行因素、运行维护因素、电量因素、电力消耗因素。再将准则层进行细分后，产生子准则层。针对设备运行因素，提出风电场可利用率、年风机平均运行时间2 个要素；针对生产维护因素，提出年风机平均非计划停机时间、年风机平均计划停运时间、度电运行维护费3 个要素；针对电力消耗因素，提出综合场用电率、购网电量、各项损失电量3 个要素；针对电量因素，提出发电量、上网电量、弃风电量、利用小时4 个要素。因此，基于AHP 的风电场运行性能评估模型的目标层、准则层、子准则层全部建立，如图1 所示。

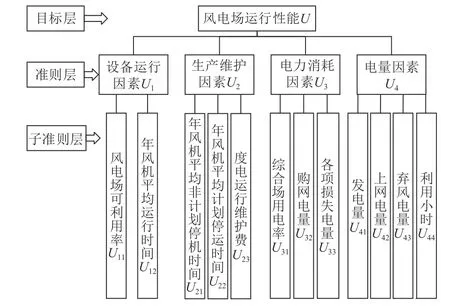
图1 风电场运行性能评价指标体系Fig. 1 Evaluation index system of wind farm operation performance

1.2 评价指标的定量计算及归一化

运行特性反映风电场的基本情况，主要是统计性指标。对于图1 中所示的运行性能评价指标，一部分指标可以从风电场的监控系统或统计报表中直接获得，部分指标需要进行计算才能得到。对于设备运行指标中的风电场可利用率，分以下2 种情况进行统计计算。

1）若风电场全部风电机组单机容量都相同，风电场可利用率即为全部风电机组实际可利用率的平均值。

2）若风电场有多种单机容量的风电机组，风电场可利用率应分别统计各容量风电机组的平均实际可利用率，再按容量加权平均，即

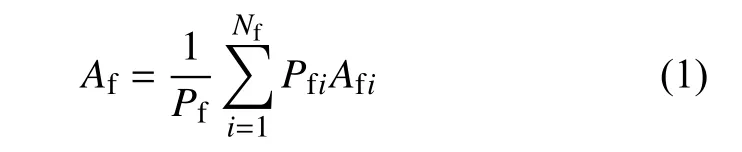
式中：Af为风电场可利用率；Pfi为第i台风电机组的容量；Afi为第i台机组的实际可利用率；Pf为总装机容量。

风电机组实际可利用率Afi的计算式为

式中：T为日历时间；TB.i为第i台机组的故障时间；TD.i为第i台机组的状态不明时间。

度电运行维护费FkWh的表达式为

式中：F为统计年度内的风电场运行维护费；Ep为风电场的发电量。

综合场用电率的计算式为

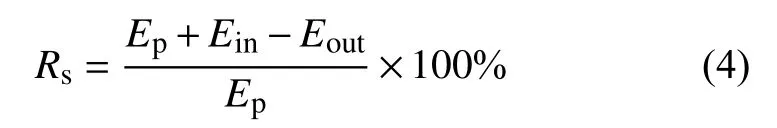
式中：Ep为发电量；Ein为用网电量；Eout为上网电量，即风电场最终向电网输送的电量，可以从风电场与电网的关口电能表取得。

电量指标中的利用小时的计算式为

由于选取的风电场运行性能评价指标的量纲和取值范围均不同，因此采用计算相对劣化度的方法对评价指标进行规范化处理，从而对不同评价指标进行统一评估。相对劣化度取值为0～1 之间，0 代表指标没有劣化，1 代表指标劣化非常严重。对风电场的运行性能评估可以分为以下2种指标计算劣化度。

越小越优型指标，如图1 中所示的U21、U22、U23、U31、U32、U33、U43，劣化度计算公式为

式中：x为指标参数的实测值；[xmin,xmax]为指标参数的正常范围。

根据上述相对劣化度的计算式，计算风电场所有评价指标的相对劣化度值，记为L={li1,li2,···,lij}，i=1,2,···,4，j=1,2,···,η，η为第i个一级指标下二级指标的个数。

参考风电场运行性能特征研究的大量相关文献，目前对风电场运行性能各指标的优劣范围赋值并无相关标准。本文将风电场运行性能的评价结果，划分为优秀、良好、中等、较差4 个等级。确定评价集W={W1，W2，W3，W4}={优秀，良好，中等，较差}。划分评价等级与相对劣化度之间的关系如表1 所示。

表1 评价等级与相对劣化度的关系Table 1 Relationship between evaluation grade and relative deterioration degree

2 层次分析法权重模型

由图可知，风电场运行性能作为总评价对象，其影响因素有设备运行因素U1、生产维护因素U2、电力消耗因素U3、电力因素U4，确定因素集U={U1，U2，U3，U4}。而将因素U1作为评价对象，其影响因素有U11、U12，则确定因素集U1={U11，U12}。同理将因素U2、U3、U4分别作为评价对象，则分别确定因素集U2={U21，U22，U23}、U3={U31，U32，U33}、U4={U41，U42，U43，U44}。

2.1 判断矩阵确定

层次分析法中的重要步骤是构建判断矩阵，关于前一层次某个要素，可对比当前层次各要素间两两相对重要性程度在目标层的设计元素U和准则层的设计元素之间创建内部关系，构建判断矩阵如表2 所示。

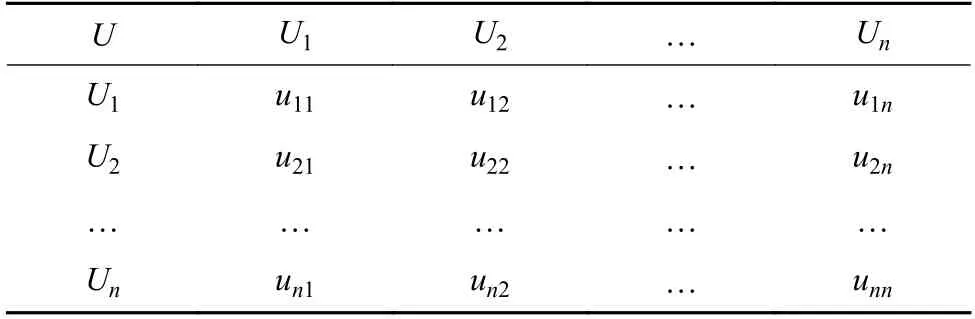
表2 判断矩阵构建方式Table 2 Build judgment matrix

表2 中，uij表示某要素与前一层次要素U做对比时，要素Ui相对于要素Uj的重要性，若相反则取倒数为1/uij。所以，在判断矩阵中，uii＝1，uij＝1/uji。判断矩阵的标度利用模糊数值定义为1～9 的整数来表示,即用数字1～9 及其倒数来表示uij。因素相对重要程度评分规则表如表3 所示。

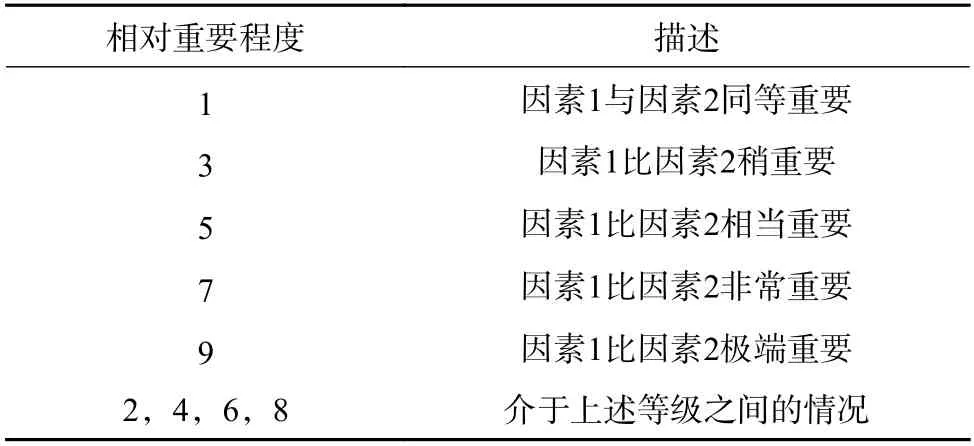
表3 因素相对重要程度评分规则Table 3 Scoring rules for relative importance of factors

2.2 一致性检验模型

计算权重后，需对判断矩阵进行一致性检验,从而保证前后判断的一致性。在进行一致性检验时，采用一致性比值 ψ的大小来进行判断，若ψ ≤0.1，认为此判断矩阵在一致性方面满足条件，一致性比值 ψ的计算式为

式中：RI为随机一致性指标，对于γ阶矩阵，RI的取值如表4 所示。CI为判断矩阵的一致性指标。

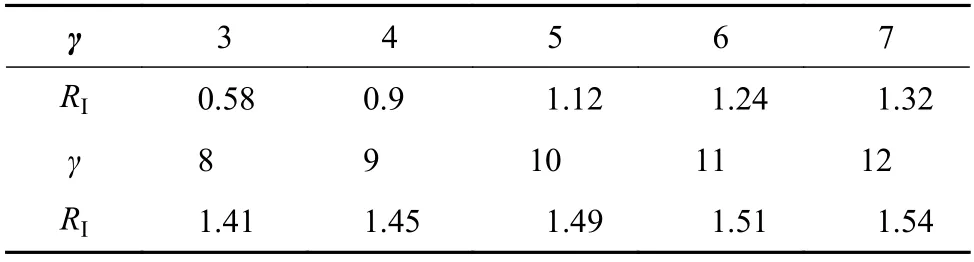
表4 γ 阶矩阵的 RI 值Table 4 Value of matrix RI of order γ

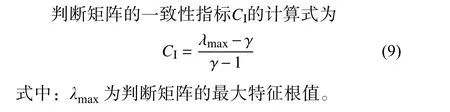
3 模糊评判矩阵的确定

3.1 正态云模型

云模型作为定性与定量之间转换的不确定性模型，充分反映了语言概念的随机性和模糊性，构建了定量与定性之间的映射。在论域空间中，由大量云滴组成的云可以代表一个特定的概念，并通过期望Ex、熵En和超熵He来进行整体表征[21]。

则x在论域Z上的分布称为正态云。本文利用正态隶属云来确定风电场运行性能评估指标的隶属度，正态隶属云生成算法流程如下：

4）重复步骤1)～3)至产生K个云滴。通过借助经验与反复试验，云滴数为1500 时此云模型综合反映随机样本数值和隶属程度的不确定性，能有效呈现随机性和模糊性间的关联。

正态云生成算法流程图如附录A 中图A1 所示。

传统云模型中数字特征的求解在数据处于阈值附近时，其相对应的确定度趋近于0，从而评估结果难以辨别：

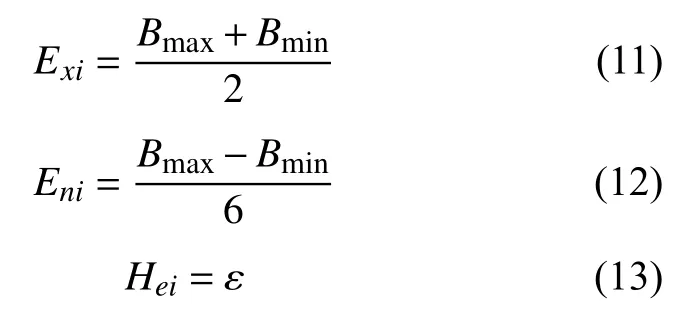
故本文对数据特征的求解公式进行改进，确定隶属云生成算法中3 个数字特征的计算式为

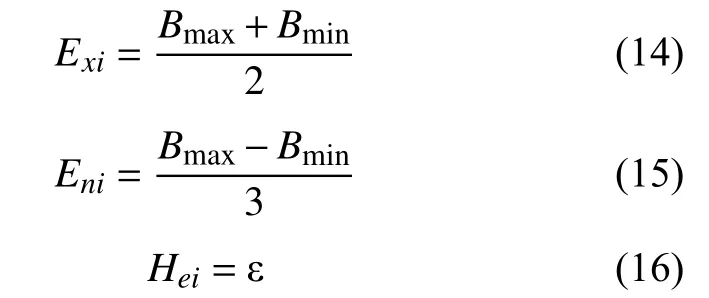
式中：i表示状态，i∈{1,2,3,4}；Bmax和Bmin分别为相对劣化度的最大和最小边界；ε 为常数，可根据变量模糊阀度进行调整，本文取ε=En/10。

结合表1 所示的相对劣化度与评价等级关系，建立云模型的数字特征如表5 所示。

运行性能状态作为一个定性概念，故本文运用正态云模型表示此概念的不确定性具有明显优势。通过云发生器，可将运行性能评价中的随机性和模糊性转换为确定度这个定量值，反映了评价过程中的随机性与模糊性之间的关联。

3.2 隶属度及判断矩阵确定

根据表5 中的数字特征，利用正态隶属云生成算法，生成运行性能评估指标的正态隶属云图如图2 所示。

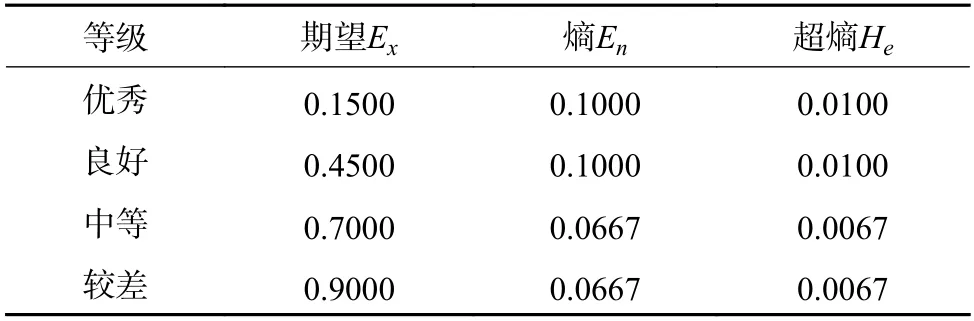
表5 云模型的数字特征Table 5 Digital characteristics of cloud model

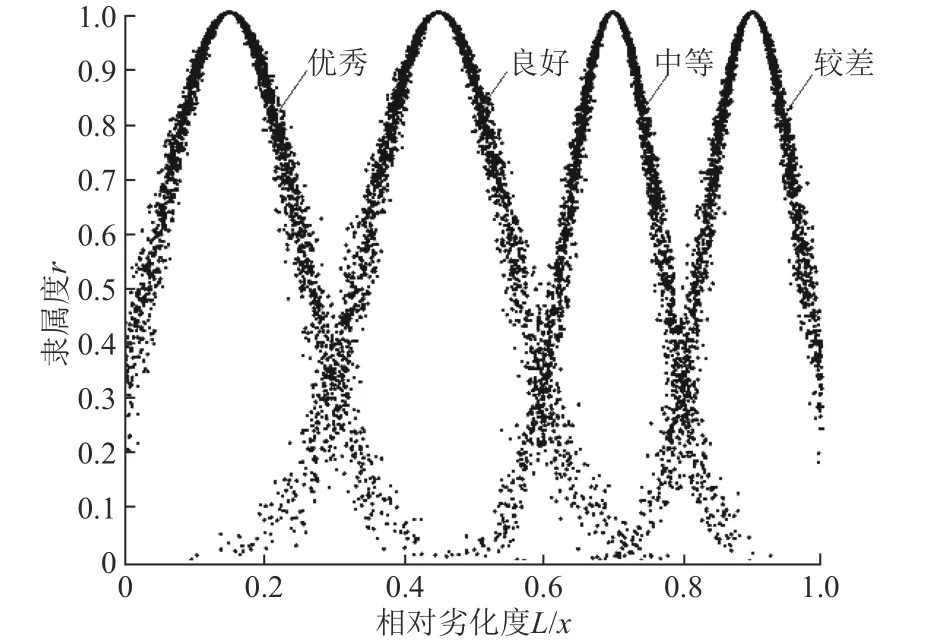
图2 运行性能评估指标的正态隶属云图Fig. 2 The chart of normal membership cloud chart of operation performance evaluation index

在图2 所示的正态隶属云中，横坐标为评价指标的相对劣化度L(x)，纵坐标为评价指标相对于评价集的隶属度r，从而得到运行性能各评价指标相对于各评价等级的隶属度确定步骤为：

1）计算风电场评价指标规范化后的相对劣化度L，根据表中的数字特征生成各评价等级的隶属云；

2）对于运行性能评估第i个一级指标下的第1 个评价指标，过L(x)=li1，作一条平行于纵坐标轴的直线，此时与图2 所示的隶属云图有M个交点，取M个交点对应的隶属度r的平均值作为该评价指标相对于某评价等级的隶属度；

3）同理，可得到其余评价指标相对于各个评价等级的隶属度。

根据各因素劣化度值和上述隶属度的计算方法，分别计算出设备运行因素、生产维护因素、电力消耗因素、电量因素的指标隶属度矩阵Rf1、Rf2、Rf3、Rf4。各隶属度矩阵Rfi可以表示为

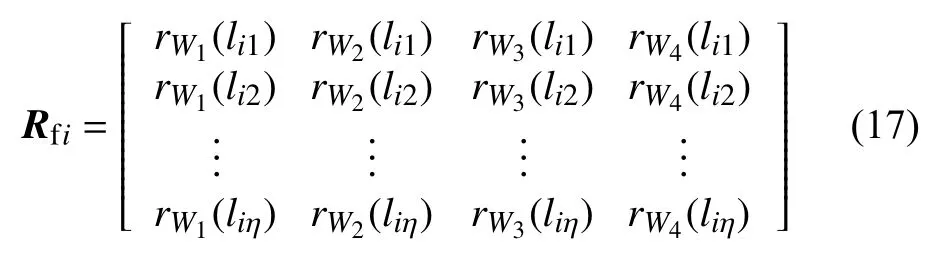
式中：i∈{1,2,3,4}，j∈{1,2,···,η}，η为第i个一级指标下二级指标的个数。

风电场运行特性评价一级指标的隶属度为

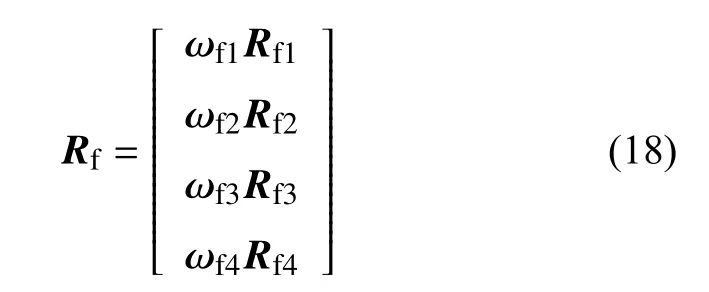
式中：ωf1、ωf2、ωf3、ωf4为二级指标的权重矩阵。

从而，风电场运行特性的模糊综合评判结果为

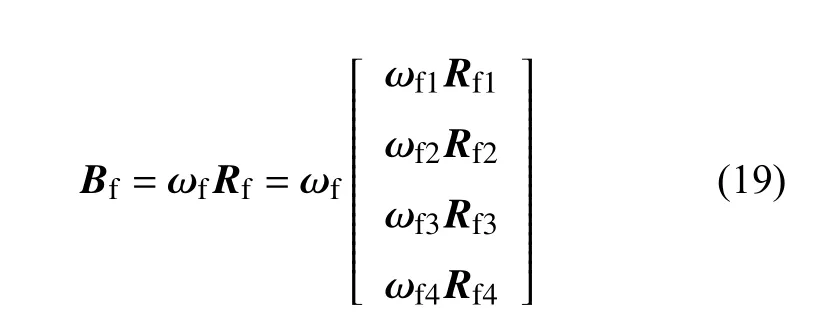
式中：ωf为风电场运行性能评价一级指标的权重矩阵；Rf为一级指标的隶属度矩阵。

采用限值矩阵对模糊变换后的矩阵进行评价，即

式中： θ为限值矩阵；Yi为风电场运行性能一级指标模糊综合评价结果的定量值；Q为最后模糊综合评价结果的定量值。

本文规定限值矩阵为

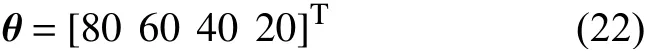
根据限值矩阵进行转换后，可以得到一个评价结果的定量值，根据定量值所在的区间对风电场运行性能水平进行评估。当定量值≥80时，评价结果为“优秀”；当60 ≤定量值<80时，评价结果为“良好”；当40 ≤定量值<60时，评价结果为“中等”；当定量值<40时，评价结果为 “较差”。

4 算例分析

为了验证本文提出的风电场运行特性评估方法的有效性，以国内某风电场2017 年的实际运行数据为例进行分析。该风电场共有风电机组56 台，单台机组的额定功率为1.5 MW，总装机容量为84 MW。根据该风电场的运行年报显示，2017 年风电场的发电量为18511.49 万kW·h，上网电量为18276.02 万kW·h，购网电量51.92万kW·h，各项损失电量623.13 万kW·h，弃风电量为619.41 万kW·h，年累计运行时间为8656.90 h，年风机平均非计划、计划时间分别为48.8393、49.625 h，全年的运行维护费用为425 万元。根据部分评价指标的计算方法，得到风电场的可利用率、度电运行维护费、综合场用电率、利用小时的值如附录C 表C1 所示。

1）根据表3 中的评分规则，判断矩阵如附录B 表B1—表B5 所示。将因素集U中各元素之间重要程度进行比较得到的判断矩阵记为X，同理，将因素集U1、U2、U3、U4中各元素进行比较，将判断矩阵分别记为X1、X2、X3、X4。对各判断矩阵分别求特征向量及最大特征值，并进行一致性校验，校验结果如附录B 中表B6 所示。

由附录B 表B6 可知，各判断矩阵的ψ<0.1，满足一致性要求。最终确定权重集为ωf=[0.2892 0.1678 0.1233 0.4197]、ωf1=[0.6667 0.3333]、ωf2=[0.2628 0.0786 0.6586]、ωf3=[0.5470 0.1085 0.3445]、ωf4=[0.3118 0.5363 0.0555 0.0964]。

2）根据该风电场各评价指标的值和隶属度的确定方法，从而可以确定各因素集对评价集的模糊关系矩阵[Rfi，i∈{1,2,3,4}。]

3）对因素集U1、U2、U3、U4分别进行模糊关系变换，得到各因素集对于评价集的隶属度向量Bfi，i∈{1,2,3,4}。

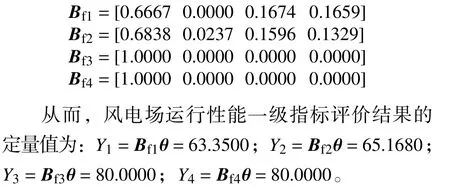
根据评分规则，确定2017 年该风电场运行性能4 个一级指标（设备运行因素、生产维护因素、电力消耗因素、电量因素）的结果分别为“良好”、“良好”、“优秀”、“优秀”。

4）将因素集U={U1，U2，U3，U4}作为评价对象，各因素U1、U2、U3、U4视为U中的因素，因此得到因素集U对于评级集W的模糊关系矩阵Rf。

对因素集U进行模糊关系变换，最终得到因素集U对于评价集W的隶属度向量Bf。

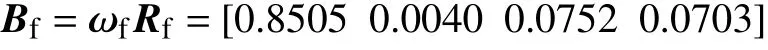
5）风电场运行性能综合评价结果的定量值为

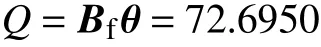
根据评分规则，确定2017 年该风电场运行性能的评价结果为“良好”。结合4 个一级指标的评价结果，通过对评价结果相对较差的一级指标的相关影响因素进行分析，并进行相应地改进，将有助于提高风电场整体的运行性能，从而进一步提高风电场的经济效益。

为进一步验证本文提出的风电场运行性能评价方法的有效性，利用该风电场2016—2018 年的运行数据，将本文方法与常用多指标综合分析方法进行对比。该风电场2016—2018 年各指标数据如附录C 表C12 所示，方法对比排序结果如表6 所示，其中1—3 表示评价结果优劣排序，1为最好。

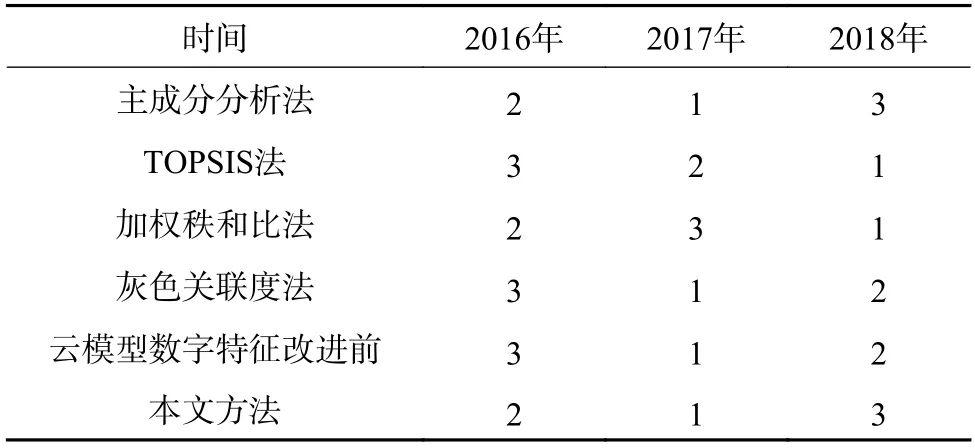
表6 不同方法的2016—2018 年风电场运行性能评估结果排序Table 6 Ranking of evaluation results of wind farm operation performance evaluation results by different methods in 2016—2018

由附录C 表C2 可知，2017 年的各项指标大都优于另外2 年，其中包括反映风电场经济效益的发电量、上网电量以及各项损失电量等指标。根据表6 中的排序结果，利用本文方法，该风电场近3 年的运行性能排序结果为：2017 年>2016年>2018 年，通过对比附录C 表C2 中的各项指标数据，可知评价结果与实际运行情况相符。算例分析结果中，主成分分析法与本文方法结果一致，但主成分分析法用于综合评价函数的意义不太明确。本文所提方法将与风电场运行情况评价有关的因素进行分解，然后进行综合评价，更能反映风电场的综合运行性能。改进后的云模型数字特征计算公式中，当评价指标数据取到阈值附近时，可提高评价结果的区分度。本文方法在指标数和影响因素较多的情况下，能较明确地反映风电场运行中存在的问题，从而针对该因素提出科学有效的治理措施，以进一步提高风电场的经济效益，更加符合实际运行评价需求。