汽车悬置系统固有特性的混合不确定性传播与可靠性分析

黄晓婷 郑泽滨 郑静远 吕 辉

(1. 广州城市理工学院汽车与交通工程学院 广州 510800； 2. 华南理工大学机械与汽车工程学院 广州 510641)

发动机振动是汽车振动的主要来源之一，汽车动力总成悬置系统(Powertrain mounting systems, PMS)的隔振性能直接影响着发动机振动向车身传递。在实际工程中，受结构复杂性、加工制造以及材料老化等因素影响，PMS不可避免地存在各种不确定因素[1-2]。因此，当系统参数存在不确定性时，有必要对PMS的固有特性开展不确定性传播和可靠性分析研究。

当系统参数信息充足时，随机模型是处理PMS不确定性传播和优化设计问题最常用的工具[3-4]。Xin等[5]开展了电动汽车悬架刚度参数为正态随机变量的多目标优化。张武等[6]分别基于3σ和6σ的随机模型开展了PMS解耦率的稳健性优化设计。系统参数信息匮乏的情况下，难以精确构建随机模型。为此，一些非概率模型受到了广泛关注，如区间模型[7]和模糊模型[9]等。Cai等[8]将Chebyshev级数展开与顶点法相结合，提出了一种PMS区间不确定性传播分析的高效方法，并进一步用于PMS的优化设计。基于模糊模型，吕辉等[9]开展了含模糊不确定性的PMS固有特性的可靠性分析与优化。

上述的PMS不确定性研究均基于单一的不确定性模型开展，没有考虑到PMS可能存在一部分参数信息充足而另一部分参数信息不足的混合不确定情形。针对这种情形，Cai等[10]基于随机与区间混合不确定性模型，提出了一种混合不确定情形下PMS的不确定性传播分析方法。工程中，PMS还可能遇到一部分参数因信息充足可视为随机变量，另一部分参数因存在模糊特性而视为模糊变量的混合不确定情形。目前，随机与模糊不确定情形下PMS的不确定性传播分析和可靠性分析研究尚不多见。

本文旨在开展随机与模糊混合不确定情形下PMS固有特性的不确定性传播分析和可靠性研究。首先引入随机与模糊混合不确定性模型处理系统参数；然后提出一种求解PMS固有频率和解耦率不确定性响应的蒙特卡洛法；接着将泰勒展开和中心差分法相结合提出一种快速求解PMS固有特性响应的混合摄动中心差分法；再基于模糊可靠性和准则提出一种PMS固有特性的可靠性分析方法。通过算例验证了方法的有效性。

1 PMS的固有特性

1.1 固有频率

PMS一般通过若干个悬置将动力总成支撑在车架上，动力总成可视为一个刚体。图1给出了某一PMS的6自由度动力学模型。该模型中，悬置被简化为具有三向刚度和阻尼特性的弹性元件。由于悬置阻尼对系统固有特性影响很小，因此PMS通常被视作无阻尼的自由振动系统。其运动方程为：

图1 PMS动力学6自由度模型Fig.1 Six degree-of-freedom model of PMS

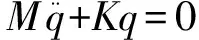
(1)

其中，M和K分别为PMS的质量和刚度矩阵；q为PMS广义坐标的位移向量。

求解式(1)可得PMS的固有频率及对应的振型：

ft=ωt/2π，φt={φ1t,φ2t,…φ6t}T,

t=1,2,…6

(2)

其中ft代表第t阶固有频率，φt表示第t阶振型。

1.2 解耦率

当PMS以第t阶固有频率振动时，第t阶振型振动能量分布为：

(3)

其中k表示第k个主坐标系列向量；Mkl为M的第k行第l列元素；φkt和φlt分别为φt的第k个和第l个元素。第t阶模态的解耦率定义为:

dt=max{E(k,t)},t=1,2,…6

(4)

dt越大，表明第t阶方向的振动解耦程度越高。

2 PMS固有特性的混合不确定性传播分析

2.1 随机与模糊混合不确定性模型

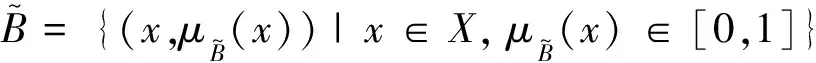
(5)

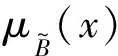
(6)

(7)

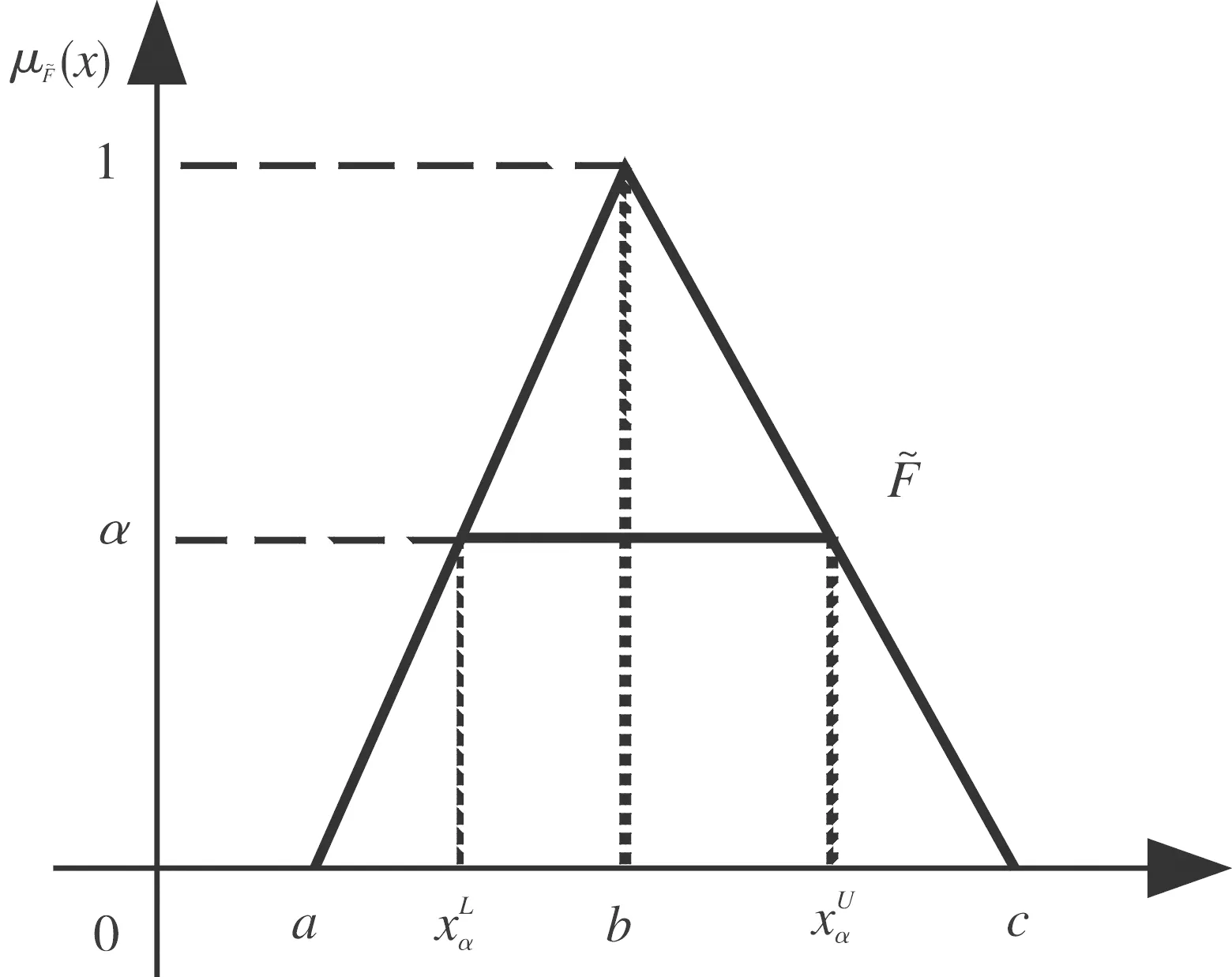
图2 三角模糊数Fig.2 A triangular fuzzy number

实际工程中，PMS中可能存在这样的不确定情形：一部分参数信息充足适合采用随机变量描述；另一部分参数由于缺乏足够的数据而具有模糊特性，宜采用模糊变量来描述。这种情形下，PMS的固有特性响应S(Y)可表示为：

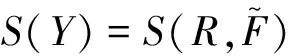
Y={Y1,Y2,…Yn}T

R={R1,R2,…Rm}T

(8)

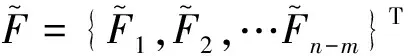
2.2 不确定性传播的蒙特卡洛法

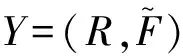
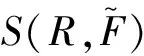
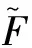
(3)对随机变量R进行随机抽样，记为R(q)，q=1,2,…Q，Q为随机抽样次数。

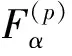
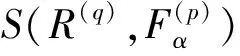
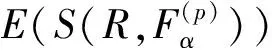
2.3 不确定性传播的混合摄动中心差分法

E(YFα)=E(Y1,Fα,Y2,Fα,…Yn,Fα)=

(E(Y1,Fα),E(Y2,Fα),…E(Yn,Fα))

V(YFα)=V(Y1,Fα,Y2,Fα,…Yn,Fα)=

(V(Y1,Fα),V(Y2,Fα),…V(Yn,Fα))

(9)

区间向量Fα可表示为：

(10)

为求解S(YFα)，先假定Fα为常数向量，则S(YFα)变成一随机函数。基于随机矩法[13]，一阶原点矩和二阶中心矩分别代表随机函数的均值和方差。S(YFα)在YFα均值处的泰勒展开式为：

(Yi,Fα-E(Yi,Fα))×(Yj,Fα-E(Yj,Fα))+…

(11)

忽略高阶项(二阶及以上)，S(YFα)的均值和方差可以近似为:

E(S(YFα))≈S(E(YFα))

(12)

Cov(Yi,Fα,Yj,Fα)

(13)

其中E(·)，V(·)和Cov(·)分别表示均值、方差和协方差函数；YFα的变量相互独立时上式可简化为：

(14)

重新考虑区间变量Fα对S(YFα)的影响，上述E(S(YFα))和V(S(YFα))以及S(YFα)的一阶偏导均是Fα的函数。E(S(YFα))和V(S(YFα))在Fα中点处的一阶泰勒展开式为[14]：

(15)

(16)

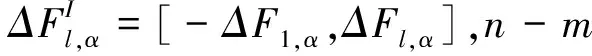
(17)

(18)

其中δFl,α≤ΔFl,α，δFl,α为Fl,α微小增量，δFl,α={0,…δFl,α,…0}T。当Fα不确定水平较小时，δFl,α可用ΔFl,α来近似替代，则式(17)和式(18)可改写为：

(19)

(20)

将式(19)和式(20)分别代入式(15)和式(16)中可得到：

(21)

(22)

根据区间算法，E(S(YFα))和V(S(YFα))的上下界可以近似为：

(23)

(24)

(25)

(26)

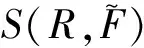
3）SAGD污水处理方式中，如MVC和MVR之类的蒸发式污水处理技术较为成熟且应用前景广泛，因此考虑结合MVC和MVR来进行余热回收利用的方案设计。

3 PMS固有特性的可靠性分析

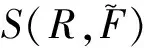
(27)

结合可靠性分析理论，分别定义SI(R,Fα)大于Smin和SI(R,Fα)小于Smax的极限状态函数为：

M1,α=SI(R,Fα)-Smin

(28)

M2,α=Smax-SI(R,Fα)

(29)

一个区间数大于或小于另一个区间数的可能性可以采用区间可靠度进行量化。根据区间可靠度，在截集水平α处，SI(R,Fα)大于Smin和SI(R,Fα)小于Smax的可靠度h1(α)和h2(α)可以分别定义为：

h1(α)=Poss(M1,α=SI(R,Fα)-Smin>0)=

(30)

h2(α)=Poss(M2,α=Smax-SI(R,Fα)>0)=

(31)

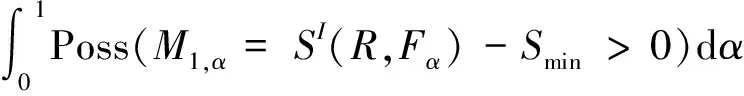
(32)

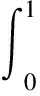
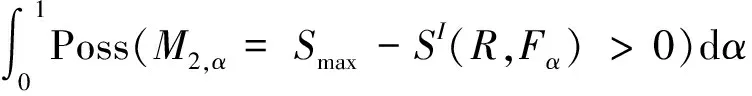
(33)

4 算例分析

4.1 分析模型

为验证所提出方法的有效性，以图 3所示的PMS模型为研究对象进行分析，相关参数取值如表 1-表 4所示。

图3 PMS示意图Fig.3 PMS schematic diagram

表1 动力总成质量、转动惯量与惯性积Table 1 Mass，moment of inertia and product of inertia of powertrain

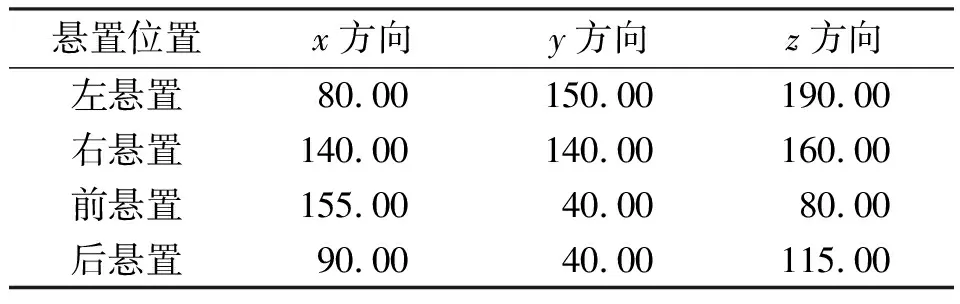
表2 悬置的初始刚度(单位：N·mm-1)Table 2 Initial stiffness of each mount (unit: N·mm-1)

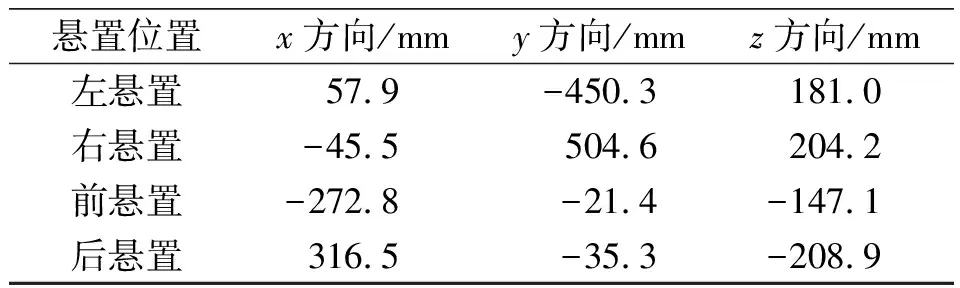
表3 悬置的安装位置Table 3 Assembly location of each mount

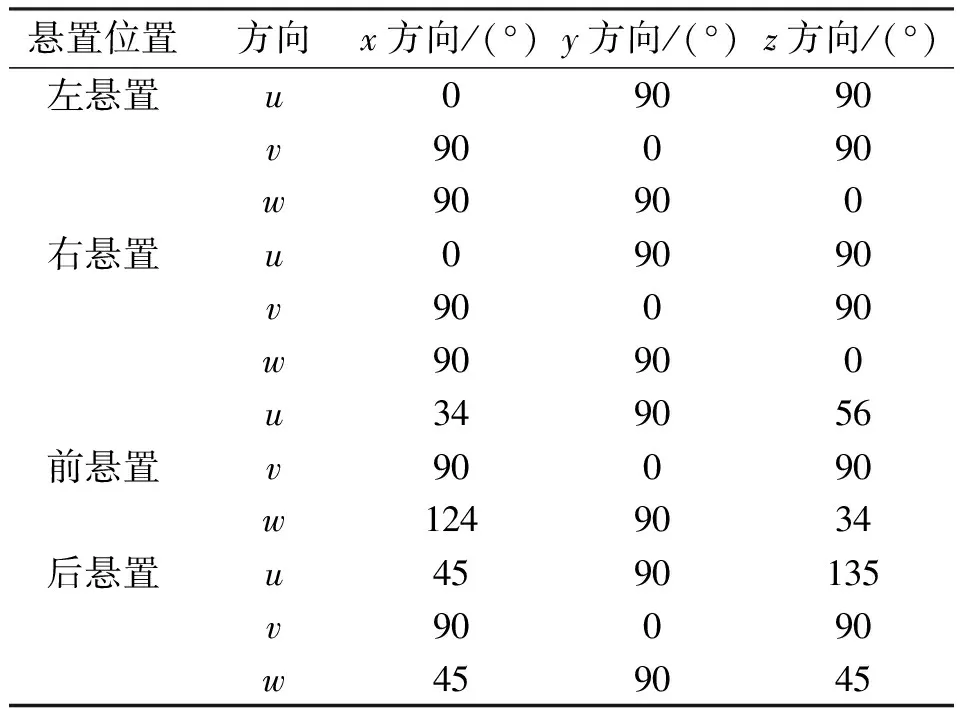
表4 悬置的安装角度Table 4 Assembly orientation of each mount

绕曲轴中心线旋转方向(Pitch方向)是发动机主要的振动激励方向，本文将重点研究该方向的固有特性，即固有频率fP和解耦率dP，其中下标P指Pitch方向。

结合工程实际，将悬置安装位置参数视为服从正态分布的随机变量，其均值为各参数初始值，标准差取3 mm。同时，将悬置静刚度视为模糊变量，用最大不确定度为±5%的三角模糊数对其进行描述，且将每个模糊数均匀划分为11个隶属度水平(α=0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0)进行分析。模糊数的相关取值如表 5所示。

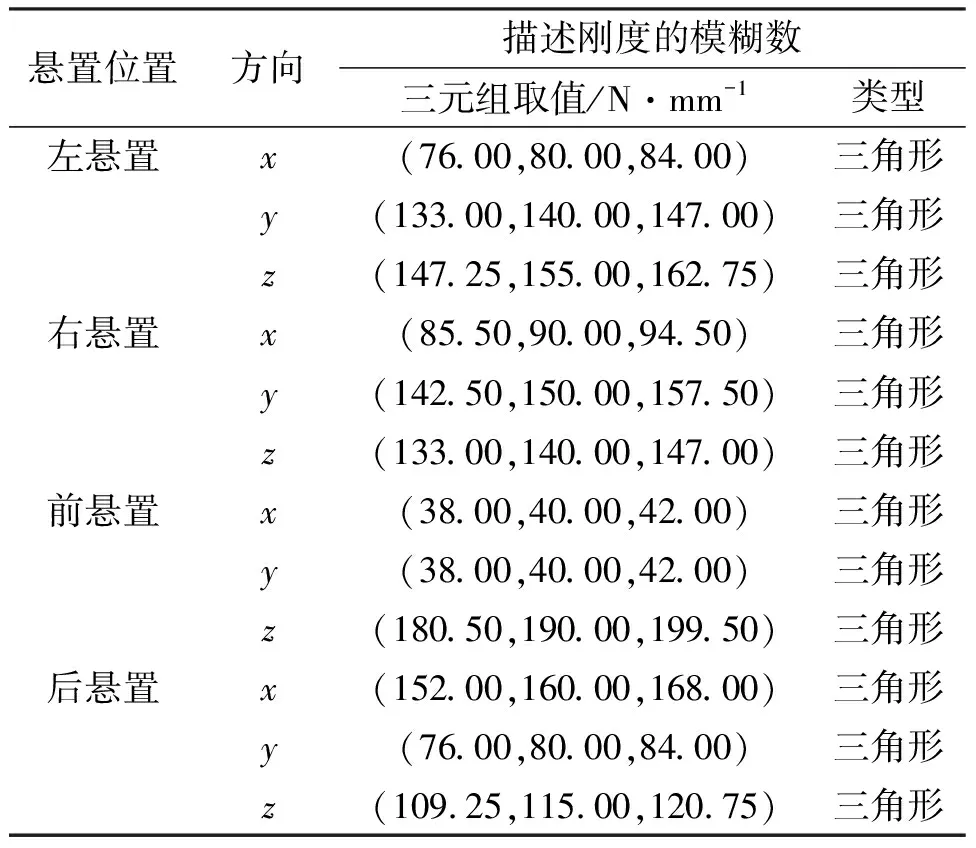
表5 模糊数取值及类型Table 5 Values and types of fuzzy numbers

此外，系统固有特性响应的设计上下限要求给定为fP,min=9 Hz，fP,max=12 Hz和dP,min=80%。由于解耦率值越大越好，故本文不对解耦率的上限进行限定，仅给出了其设计的下限要求。

4.2 不确定性传播分析

当抽样次数足够多时蒙特卡洛法能获得非常高的计算精度。因此，本文将蒙特卡洛法视为参考方法，对比分析所提出混合摄动中心差分法的计算性能。经仿真收敛性分析，选取蒙特卡洛法的抽样次数为：P=104，Q=104。图 4和表 6分别给出了固有频率fP和解耦率dP的均值和方差的响应图和响应误差。

从图 4和表 6可得出以下结论：

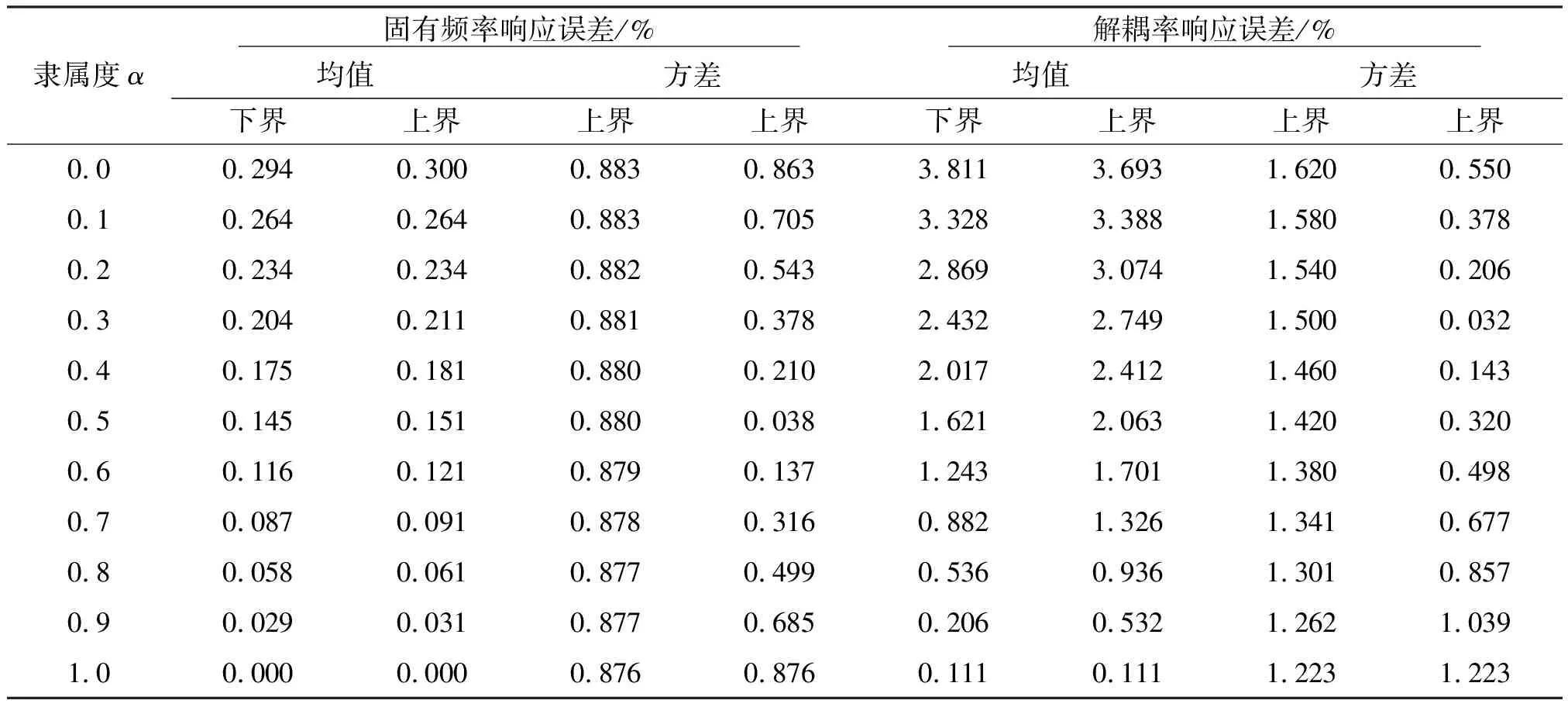
表6 固有特性的均值和方差响应的误差Table 6 Errors of expectation and variance responses of inherent characteristics

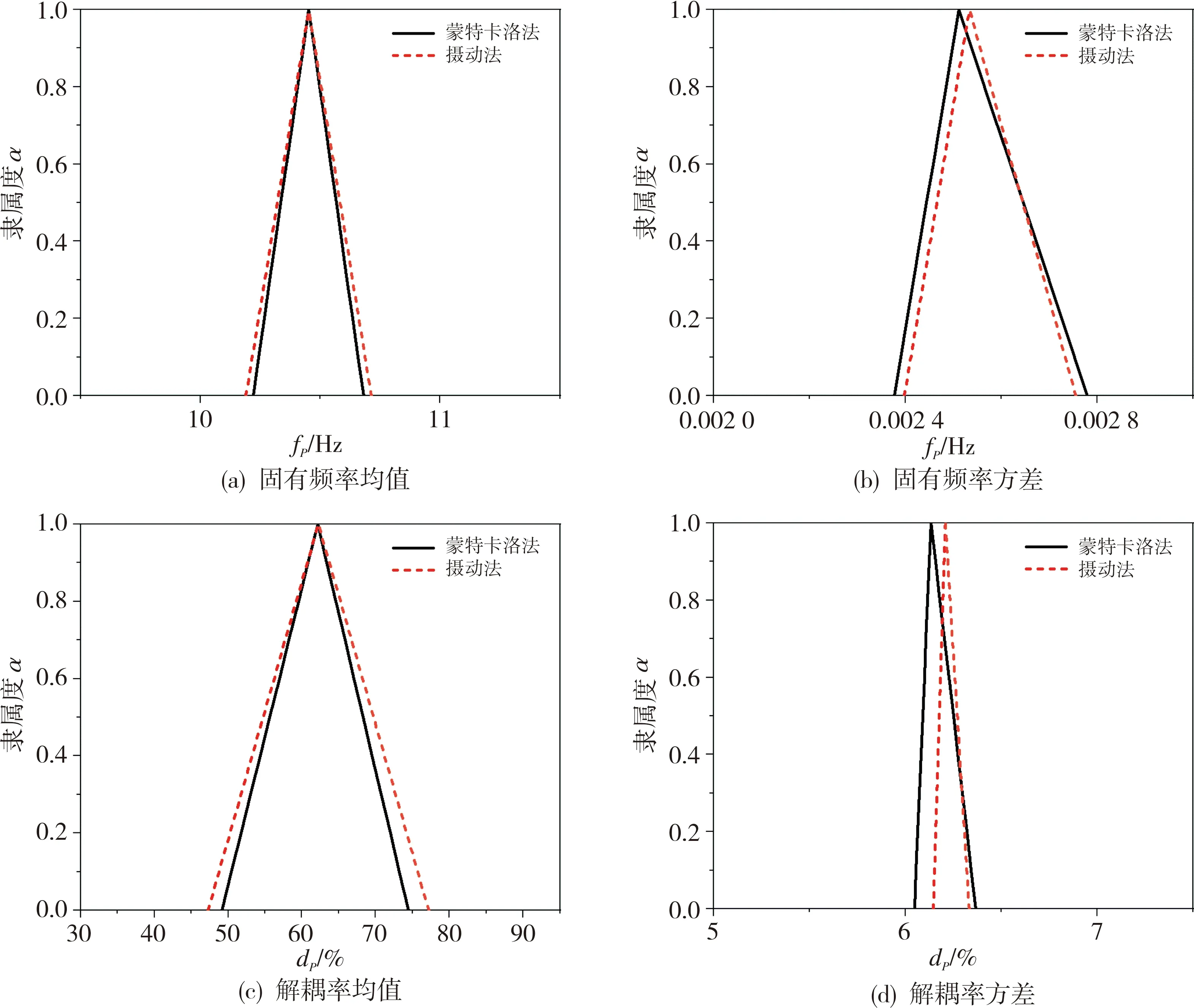
图4 固有特性的均值和方差响应Fig.4 Expectation and variance responses of inherent characteristics

(1)由混合摄动中心差分法求得的响应曲线和蒙特卡洛法获得的结果具有很好的一致性，最大的误差仅3.811%。说明所提出的混合摄动中心差分法在解决随机与模糊混合不确定情形下的PMS固有特性响应时具有较高的计算精度。此外，混合摄动中心差分法求解固有频率的精度略高于求解解耦率的精度，这是由于解耦率响应对不确定因素较为敏感。

(2)大部分情况下，随隶属度逐渐增大，混合摄动中心差分法的计算误差逐渐减小，最大误差基本处于α=0时的对应值，而在α=1.0时则最小。因此，在不确定性水平较低时，混合摄动中心差分法的计算效率更高。

在计算效率方面，蒙特卡洛法求解上述结果的时间约为17.6×104s，而混合摄动中心差分法的计算时间仅为2.13 s。因此，混合摄动中心差分法处理随机与模糊混合情形下的PMS不确定性响应时具有很好的计算效率。

4.3 可靠性分析

利用3σ准则可以将PMS固有特性的均值和方差结果进行综合考虑，并可确定固有特性响应的上下界范围。基于第4.2节的分析结果，图 5给出了利用3σ准则计算得到的固有频率fP和解耦率dP的上下界范围。为便于比较，系统固有特性响应的设计上下限要求fP,min=9 Hz，fP,max=12 Hz和dP,min=80%也分别绘在图中。

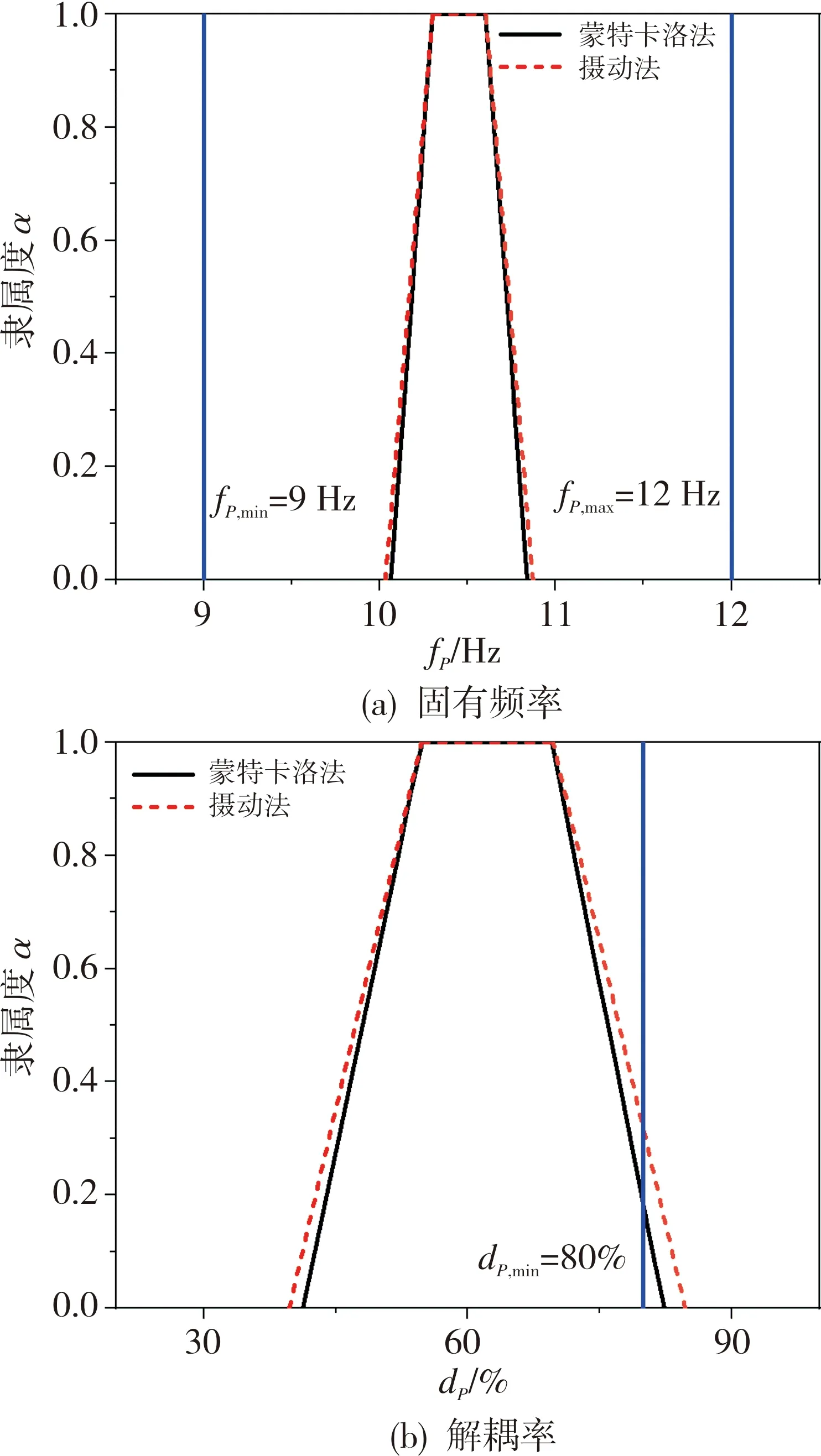
图5 固有频率和解耦率上下界范围Fig.5 Lower and upper bounds of natural frequency and decoupling rate

从图 5可得出以下结论：

(1)混合摄动中心差分法求得的固有频率和解耦率上下界范围与参考结果十分接近。这说明混合摄动中心差分法在计算随机与模糊混合不确定情形下的PMS固有特性响应上下界范围方面具有很高的计算精度。此外，两种方法求得的固有频率响应曲线几乎重合，而求得的解耦率响应曲线略有差异。这表明相对于解耦率的求解，混合摄动中心差分法在求解固有频率时具有更高的计算精度。

(2)固有频率的响应曲线完全位于其设计上下限范围之内，解耦率的响应曲线大部分位于其设计下限曲线的左边。这说明固有频率的响应完全满足设计要求，而解耦率的响应仅在一小部分情况下满足设计要求。

进一步，采用可靠度对上述结果进行度量。基于上述求得的均值和方差响应，表 7和表 8分别给出了fP和dP响应满足设计要求的区间可靠度和模糊可靠度。由于解耦率dP没有给定上限要求，故表 8 只给出了解耦率满足dP>dP,min=80%的可靠度结果。

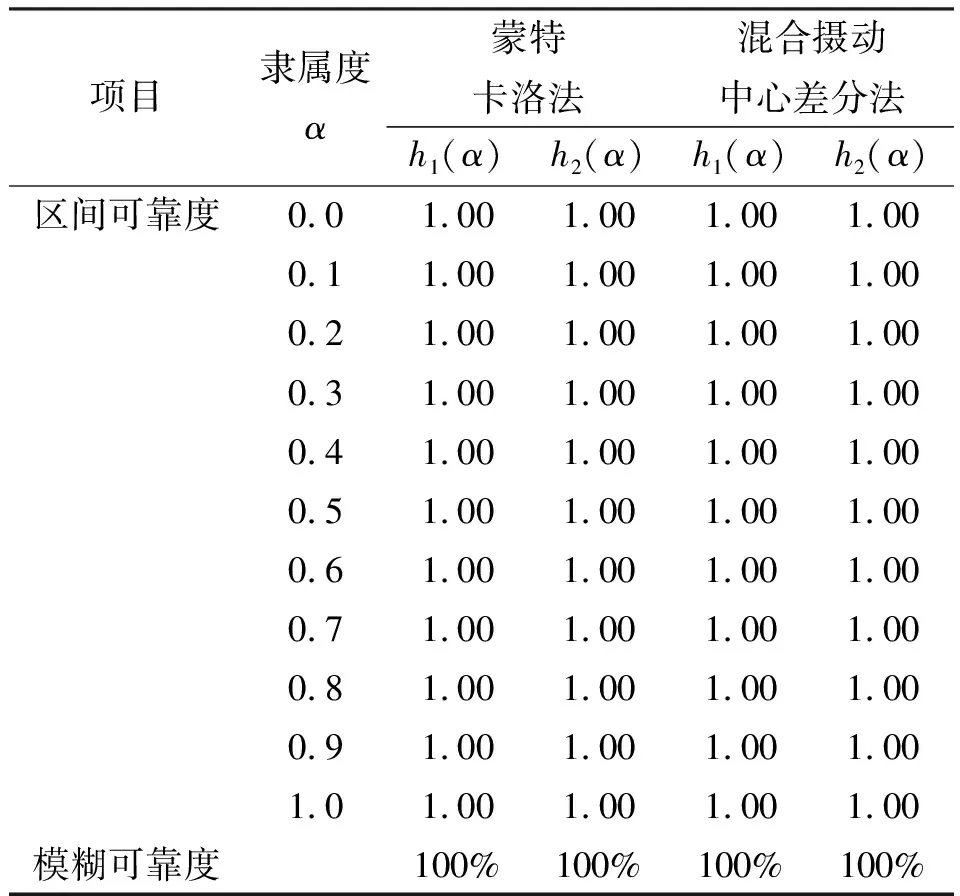
表7 fP响应满足设计要求的可靠度Table 7 Reliability of fP meeting design requirement

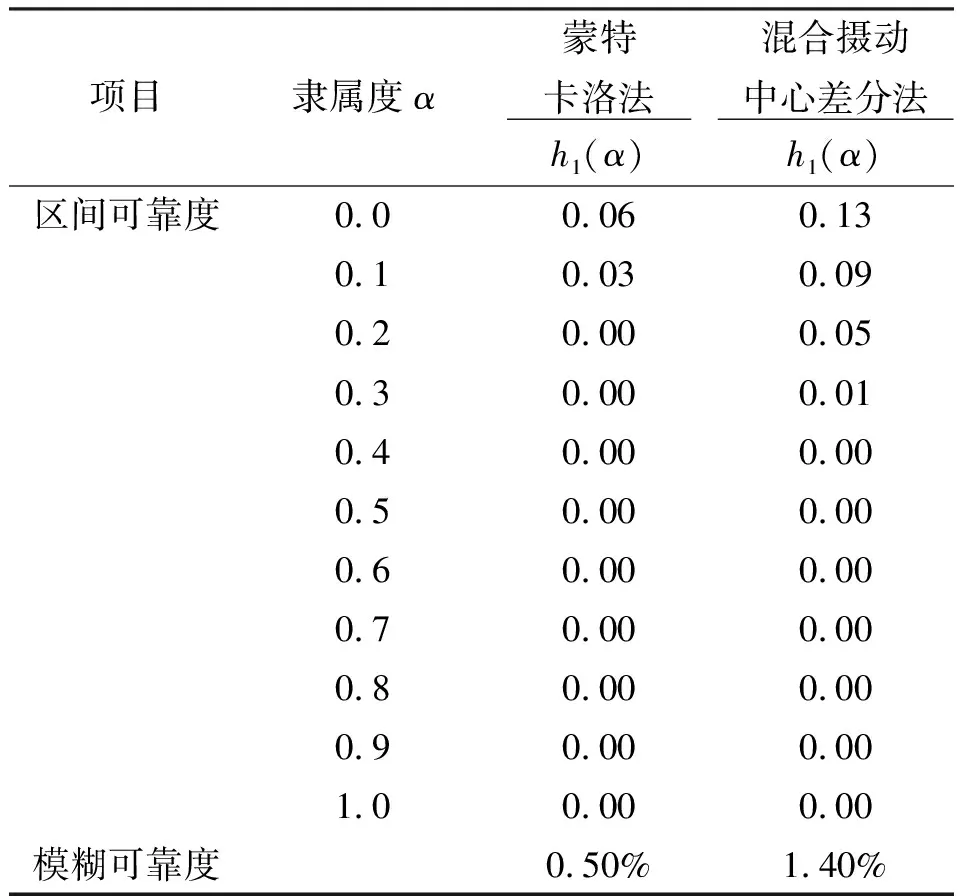
表8 dP响应满足设计要求的可靠度Table 8 Reliability of dP meeting design requirement

从表 7和表 8可得出以下结论：

(1)固有频率fP满足设计要求的区间可靠度和模糊可靠度均为100%，这说明在随机与模糊混合不确定情形下系统的fP响应完全满足给定的上下限设计要求。此外，两种方法求得fP响应的区间可靠度和模糊可靠度结果完全一致，说明混合摄动中心差分法可有效用于处理随机与模糊混合不确定情形下的固有频率可靠性分析。

(2)对于解耦率dP，两种方法求得其满足设计要求的模糊可靠度分别为0.50%和1.40%，结果差异不大，求得的可靠性结果具有较好的一致性。此外，两种方法求得的模糊可靠度值远小于100%，这说明在随机与模糊混合不确定情形下dP的响应几乎不满足设计下限的要求，后续需要进行优化设计。

5 结束语

本文开展了随机与模糊混合不确定情形下汽车PMS固有特性的不确定性传播和可靠性分析研究。引入随机与模糊混合不确定性模型处理了PMS同时存在的随机变量和模糊变量，提出了求解PMS固有频率和解耦率响应的蒙特卡洛法和混合摄动中心差分法，并提出了一种PMS固有特性的可靠性分析方法。算例分析结果表明，所提出的混合摄动中心差分法能有效处理随机与模糊不确定情形下PMS固有特性的不确定性响应分析以及可靠度计算。以蒙特卡洛法为参考，混合摄动中心差分法具有较高计算精度和计算效率。本文所提出的可靠性分析方法可为PMS固有特性优化设计提供参考。