考虑炮弹质心偏离影响的摆弹机系统振动特性分析

岳鹏飞，王德石，赵洋，刁诗靖

(海军工程大学 兵器工程学院，湖北 武汉 430033)

摆弹机是大口径舰炮实现弹药自动化转运的关键机构，它将炮弹由扬弹系统交接给发射系统，其动作可靠性影响舰炮高发射率的实现。以往研究将摆弹机简化为一个末端带质量的旋转悬臂梁[1-2]，仅考虑摆弹臂弯曲变形[3-4]的影响。实际上炮弹质心偏离摆弹臂轴线，炮弹姿态扰动引起的惯性激励力导致摆弹臂呈现弯扭耦合振动规律[5-7]，使得摆弹臂振动位移不再局限于上摆运动平面内，这对于摆弹机转运弹药的可靠性造成较大影响。因此，研究摆弹机系统弯扭耦合动力学，对于提高其动作可靠性具有重要意义，反映了舰炮自动机设计的迫切需求。

摆弹机需要在较短时间内完成上摆动作，并与转弹机完成弹药交接，针对摆弹机动力学和优化设计等问题成为学者们关注的热点。考虑到摆弹臂弹性变形引起机构运动误差，文献[8]通过动力学误差分析确定了摆弹和转弹接口应满足的误差裕度。文献[9]结合支持向量回归机与蒙特卡洛法，分析了摆弹机构的可靠性灵敏度。针对舰炮传统供弹系统结构复杂的问题，文献[10]根据变胞理论提出了一种新型弹药装填机构，建立了刚柔耦合动力学模型，研究了机构末端运动误差。文献[11-12]综合考虑扬、摆动作，设计了一型两自由度的弹药协调器，基于一种给定的隐式李雅普洛夫函数给出了协调器的位置控制算法。

不同于在平面坐标系中研究摆弹臂转动和弯曲变形耦合的振动响应，本研究考虑炮弹质心偏离引起的惯性效应，在空间坐标系中建立摆弹机系统弯扭耦合模型，根据Hamilton原理推导出时变方程，利用振型叠加法将动力学方程离散，结合数值算例分析炮弹质心位置变化对摆弹机振动特性的影响规律，研究结果对于提高供弹系统交接弹药的可靠性具有应用价值。

1 物理模型

摆弹机储能机构利用炮身复进动作为上摆弹簧储存能量，当炮弹由扬弹机送入抱弹器后，压缩状态的上摆弹簧带动齿条进行水平运动，齿条通过圆柱齿轮带动摆弹臂开始上摆动作。图1为摆弹机系统动力学模型。为了研究摆弹机系统的振动响应，作如下假设：摆弹臂横截面积为定值，其剪切中心轴与质心轴重合；摆弹臂的横截面在扭转振动过程中仍保持为平面；不考虑摆弹臂轴向变形量的影响。

如图1所示，摆弹臂绕圆柱齿轮中心O转动，摆弹臂长为L，单位长度线密度为ρ(x)，摆弹臂单位长度转动惯量为J，截面惯性矩为I，杨氏弹性模量为E。以O点为圆心建立惯性直角坐标系X0Y0Z0，OX0Y0平面坐标系描述摆弹臂大范围转动，Z0轴与摆弹臂旋转轴重合。将OX0Y0平面绕Z0轴逆时针转动θ，形成坐标系X1Y1Z1，摆弹臂横向变形量为u(x,t)，上摆弹簧提供的驱动力矩为τ。

根据文献[8]，驱动力矩可以表示为

τ=(F0-kr0θ)r0,

(1)

式中：F0为初始压力；k为上摆弹簧刚度；r0为圆柱齿轮半径。

如图2所示，以摆弹臂轴线上某点S为坐标原点，建立直角坐标系X2Y2Z2，其中Z2轴与Z0轴平行，X2轴在OX1Y1平面内并且与X1轴成角θs，Y2轴方向由右手螺旋定则确定。将SY2Z2平面绕X2轴逆时针(向X2负方向看去)旋转φ，形成直角坐标系X3Y3Z3，摆弹臂扭转角位移为φ(x,t)。假设坐标系X1Y1Z1的单位方向矢量分别为ξ1(t)、η1(t)和ζ1(t)，坐标系X3Y3Z3的单位方向矢量分别为ξ3(t)、η3(t)和ζ3(t)。

为便于研究，将摆弹臂简化为半径为R的等截面圆柱体，取长度为dx的微元为研究对象，微元段内某点的矢径R(t)可以表示为

R(t)=ξ1(t)x+η1(t)u(x,t)+

rcosγη3(t)+rsinγζ3(t),

(2)

式中,r和γ均为柱坐标参数。

如图3所示，将炮弹和抱弹器整体视为质量为m的刚体，质心为Q，摆弹臂末端切线延长线与炮弹质心所在横截面的交点为P，摆弹臂末端距P点距离为c，定义为炮弹质心离心距，P点和Q点之间距离为e，定义为炮弹质心偏心距。先将OX1Y1平面绕Z1轴逆时针转动θd，再将其沿X4轴方向平移至原点与P点重合形成坐标系X4Y4Z4，Q点在Z4轴上，θd为炮弹质心相对于未变形摆弹臂轴线的角位移。将PY4Z4平面绕X4轴逆时针(向X4轴负方向看去)旋转φd，得到直角坐标系X5Y5Z5，其单位方向矢量分别为ξ5(t)、η5(t)和ζ5(t)，φd为炮弹扭转角位移。

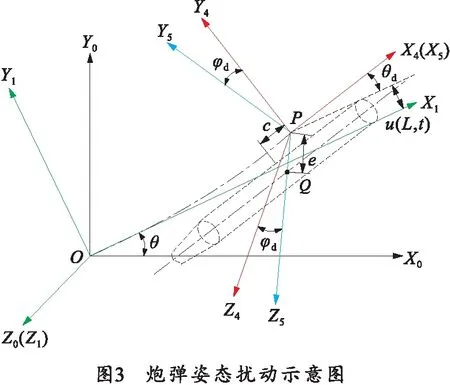
用r(t)表示炮弹质心Q的矢径，有

r(t)=ξ1(t)L+η1(t)u(L,t)+

ξ5(t)c+ζ5(t)e.

(3)

2 系统动力学方程

考虑到θs，φ，θd和φd数值较小，根据式(2)、(3)，系统动能可以表示为

(4)

式中：Th为圆柱齿轮动能；J0和JE分别为过炮弹质心相对于Z4轴和X4轴平行线的转动惯量。

系统势能包括弹性变形势能和重力势能，有

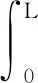
(u(L,t)+cu′(L,t)-eφ(L,t))sinθ],

(5)

式中：G为剪切弹性模量；Ip为摆臂截面极惯性矩。

根据假设模态法和分离变量法，摆弹臂横向振动和扭转振动的解可以表示为

(6)

(7)

式中：i为模态阶数；N为模态截断数；Yi(x)和Φi(x)分别为第i阶横向振动和扭转振动的振型函数；Ai(t)和Bi(t)分别为对应的第i阶模态坐标。

外力矩对系统做功可以表示为W=τθ，根据Hamilton原理，可以得到系统动力学方程

(8)

式中,M、C、K均为2N+1阶矩阵。

角速度以及系统振动响应的时变性引起M、C、K矩阵的时变性，矩阵中非零元素的具体形式为

M11=J0+Jh+m[u(L,t)+cu′(L,t)-eφ(L,t)]2+

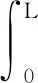
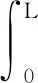
m(L+c)(Y(L)+cY′(L)),

M13=-me(L+c)Φ(L),

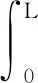
m(cY′(L)+Y(L))T(cY′(L)+Y(L))+

M23=-me[cY′(L)+Y(L)]TΦ(L),

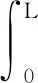
u(L,t)-eφ(L,t))(cY′(L)+Y(L)),

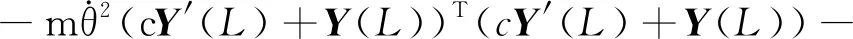
F1=τ-mg[(L+c)sinθ-eφ(L,t)cosθ+(u(L,t)+

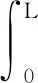
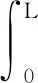
F3=mgesinθΦT(L).

3 振型函数

针对系统弯扭耦合振动方程型函数的求解问题，Sakawa[5]提出一种利用一对具有耦合边界条件的解耦偏微分方程来描述旋转梁运动姿态的动力学模型，进一步通过耦合边界条件确定振型函数的参数。根据这种方法，引入参数β，并且β>0，定义特征参数λ和α，令

(9)

(10)

在x=0处，摆弹臂横向振动和扭转振动的边界条件为

u(x,t)|x=0=0，u′(x,t)|x=0=0，φ(t,0)=0。

根据等截面Bernoulli-Euler梁模型，摆弹臂横向振动和扭转振动的振型函数分别为

Y(x)=C1[sin(βx/L)-sinh(βx/L)]+

C2[cos(βx/L)-cosh(βx/L)],

(11)

(12)

式中,Ci(i=1,2,3)为振型函数的系数。

将u(L,t)、u′(L,t)和φ(L,t)作为广义变量，相对应的广义力可以表示为

f1=EIu‴(L,t)，f2=-EIu″(L,t)，f3=-GIpφ′(L,t)。

根据第二类Lagrange方程，得到炮弹姿态控制方程组

(13)

在自由振动条件下，式(13)的振型函数为

(14)

将式(11)和(12)代入式(14)中以确定系数Ci(i=1,2,3)的值，可以得到

(15)

方程(15)存在非零解的条件是|aij(β)|=0。根据求得βi(i=1,2,…)的值，定义变量

(16)

综合式(11)、(12)和(16)，可以得到第i阶模态对应振型函数为

(17)

(18)

采用四阶龙格-库塔法求解方程(8)，针对某一求解时刻，将该时刻的计算结果以及对应的M、C、K矩阵的值作为下一求解时刻的初值进行迭代计算。

4 数值仿真

针对某型大口径舰炮进行数值仿真计算，射击状态为平射，根据供输弹系统结构原理可知，为了实现弹药姿态与输弹通道相匹配，此时摆弹臂上摆角位移行程为90°，对应着摆弹臂由下垂直位上摆到水平同步位，定义广义坐标列阵

q=[θ,AT(t),BT(t)]T,

(19)

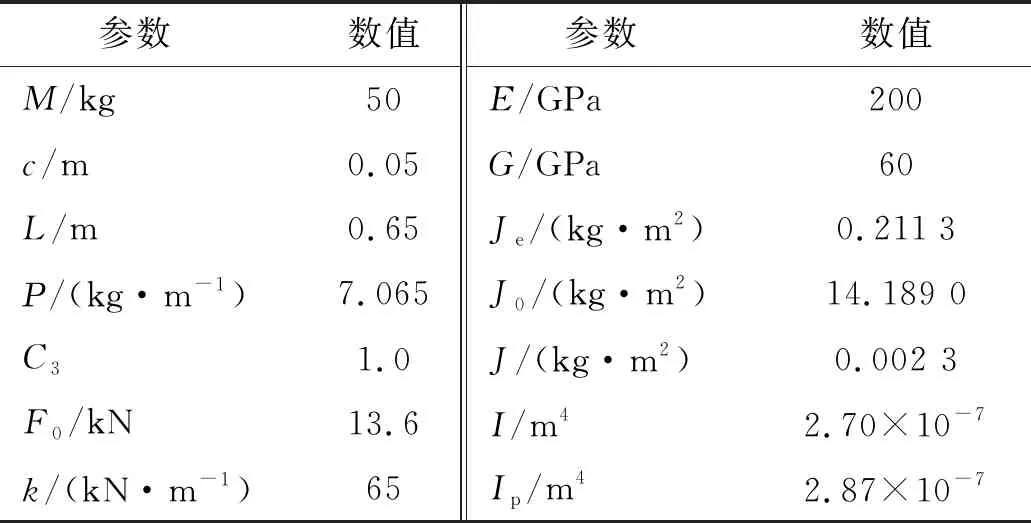
表1 物理参数

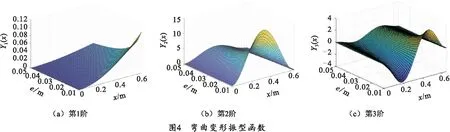
针对炮弹质心偏心距对摆弹臂振型函数的影响进行研究。取c=0.05 m，e的取值范围为0.01～0.05 m，图4、5分别为摆弹臂前3阶弯曲变形和扭转变形的振型。当e小于0.02 m时，弯曲变形振型幅值远大于扭转变形，说明质量偏心距较小时，横向弯曲振动是其主要振动形式。当e大于0.02 m时，扭转变形相对于弯曲变形的振型幅值之比减小，摆弹臂扭转振动响应逐渐凸显。根据上述分析，质量偏心距影响摆弹臂系统惯性参数的空间分布规律，相较于扭转振型，炮弹质量偏心距对弯曲振型的影响较大，随着质量偏心距增大，系统振动形式由弯曲振动逐渐转变为弯扭耦合振动。

炮弹偏心距引起摆弹臂扭转变形，炮弹离心距决定摆弹臂负载的大小，摆弹机系统振动响应是横向振动、扭转振动和大范围角运动共同作用的结果，进一步研究炮弹质心位置变化下的系统振动特性。

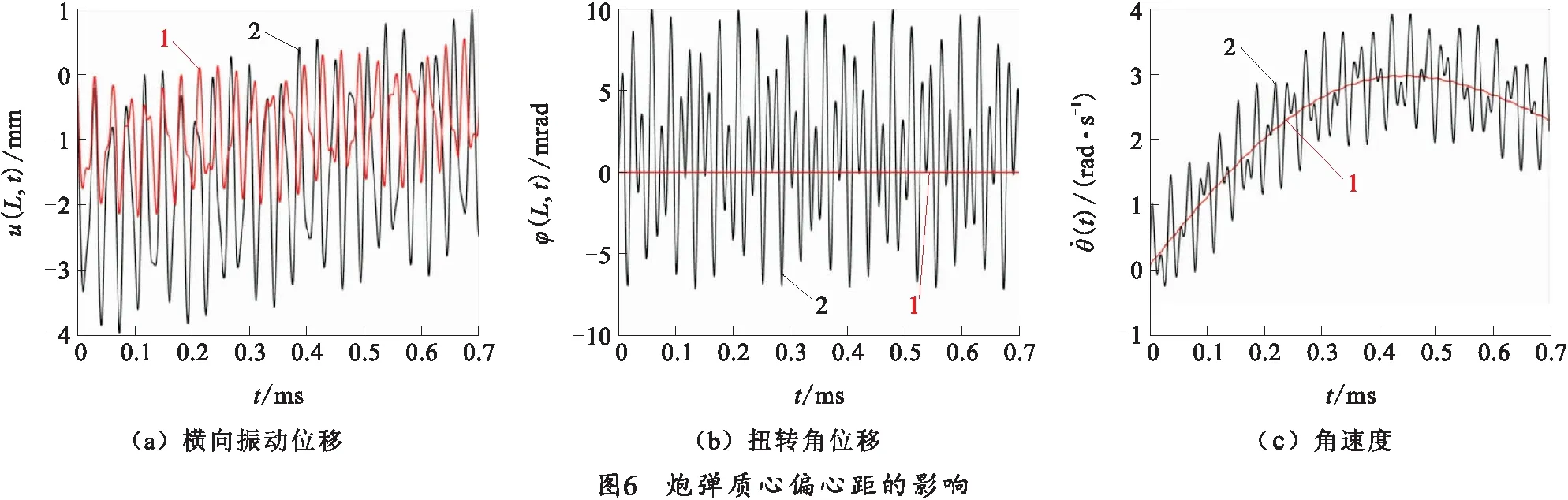
4.1 炮弹质心偏心距的影响

炮弹质心偏心距的影响如图6所示，图中曲线1表示炮弹质心偏离量e=0，曲线2表示炮弹质心偏离e=0.05 m。由曲线1可知，摆弹臂末端弯曲变形量最大幅值为2.618 mm，上摆角速度最大幅值为2.984 rad/s，上摆运动时间为0.7 s，其时间历程曲线近似为光滑曲线，波动幅度较小。由曲线2可知，摆弹臂弯曲变形量最大幅值为3.943 mm，上摆角速度最大幅值为3.914 rad/s，角速度出现较大幅度振荡，摆弹臂末端扭转角位移最大幅值为9.934 mrad。研究表明，相较于仅考虑横向弯曲变形量影响的摆弹机动力学模型，炮弹质心偏离使得摆弹机工作力学环境更加复杂，引起弯曲变形量幅值增大约50%，并且摆弹臂横截面出现幅值约10 mrad的扭转角位移，导致炮弹上摆位置偏差，影响机构交接动作可靠性，在摆弹机振动特性分析中应该考虑炮弹质心偏离的影响。

4.2 炮弹质心离心距的影响

进一步研究炮弹质心离心距对摆弹臂振动响应的影响。取e=0.03 m，在有无炮弹质心离心距两种情形下进行数值仿真。不计炮弹质心离心距情形下，如图7中曲线1所示，摆弹臂末端横向振动位移最大幅值为3.842 mm，扭转角位移最大幅值为9.778 mrad，上摆角速度最大幅值为4.083 rad/s，摆弹臂上摆运动时间0.642 s。考虑炮弹质心离心距的影响，取c=0.05m，如图7中曲线2所示，相较于曲线1的结果，摆弹臂末端振动位移最大幅值增大了2.6%，扭转角位移最大幅值增大了1.6%，上摆角速度最大幅值减小了4.3%，摆弹臂完成上摆动作延后57 ms。研究表明，考虑炮弹质心离心距条件下，摆弹机负载增大，上摆角速度减小，摆弹臂横向振动位移和扭转角位移幅值增大。综上可知，炮弹由扬弹筒传入抱弹器的初始位置影响摆弹机动态特性，机构运动误差随着弹药转运路径逐渐积累，最终影响弹药位置精度和机构动作可靠性。

5 结束语

笔者考虑炮弹质心偏离摆弹臂轴线的情形，根据Hamilton原理推导出摆弹机系统弯扭耦合振动方程，进一步将方程离散成模态坐标表示的微分方程组，分析了炮弹质心位置变化对摆弹臂振型函数和系统振动特性的影响，得到如下结论：炮弹质心偏心距是影响摆弹臂弯曲振型的重要因素。炮弹质心偏离条件下，上摆角速度出现振荡，摆弹臂末端弹性变形量幅值显著增大，影响摆弹机转运弹药精度，在摆弹机动力学分析中应该考虑炮弹质心偏离的影响。当炮弹质心离心矩增大时，摆弹臂末端振动响应幅值增大以及上摆角速度减小，引起摆弹和转弹机构交接动作时间误差。建立的摆弹机系统弯扭耦合动力学模型以及求解方法，适用于大口径舰炮旁侧路摆弹以及中腹摆弹系统的振动特性分析，对于研究摆弹机交接误差界限和提高供弹系统可靠性具有重要意义。