对核心素养下“四有好课堂”的思考
2021-12-18魏伟
魏伟

在第30个教师节前夕,习近平总书记提出了“四有好老师”的理念,即做好教师,要有理想信念、有道德情操、有扎实学识、有仁爱之心。结合初中数学课堂的教学特点,顺应学生发展的需求,笔者认为好的数学课堂也应包含“四有”——有趣、有“度”、有“动”、有“疑”,应符合学生的年龄特点与接受能力,将科学性与思想性相结合、教师的主导作用与学生的主体作用相结合、统一要求与因材施教相结合、循序渐进与系统教学相结合,将理论联系实际,巩固知识技能。
下面是笔者尝试进行的“四有好课堂”的实践探索,以苏科版八年级数学“一次函数”的教学为例。
一、教学实践
1.实验与探究。
师:随着社会的进步,交通越来越便捷,交通方式也越来越多元化。老师今天开车从家出发,发现汽车油箱的油已经不多了,决定去加油站加点油。
教师展示加油站的图片以及加油的动态视频。
师:在加油过程中,涉及哪些量?
生1:金额、油量、单价。
(这些量从视频中可以很清晰地看出来。视频的展示让课堂“有趣”,让学生“有动”。)
师:在这些量中,哪些量是不变的?哪些量是变化的?
生2:单价是不变的,金额和油量是变化的。
师:我们生活在一个瞬息万变的世界里。在这个世界里,许多事物之间是有一定联系的,比如在加油的过程中,油桶显示屏上的金额、油量、单价之间就有着一些联系。今天,就让我们用数学的眼光一起观察我们身边的这些“变化”与“联系”。
师:在刚刚加油的过程中,我们给涉及的量命名:可以取不同数值的量,也就是可以变化的量,叫做变量;数值保持不变的量叫做常量。在加油过程中,油桶显示屏上的这些量中,哪些是常量?哪些是变量?
生3:单价是常量,金额和油量是变量。
师:加完油后,老师以70km/h的速度匀速行驶。在行驶过程中,汽车行驶的路程(S)随汽车行驶时间(t)的变化而变化。在这个变化过程中,有几个量?哪些是常量?哪些是变量?
生4:在这个变化过程中,有3个量。速度是常量,因為是匀速行驶的。如果不是匀速行驶,那速度就不是常量。路程和时间是变量。
(学生在这里就很好地做到了“有动”“有疑”。)
师:一些变化过程中有两个变量,一些变化过程中有3个或多个变量,我们的探索从两个变量开始。
学生了解了我们只是从基本的开始学起,后面还有更多的知识等待挖掘。
师:到了办公室,老师在同事的桌上发现了一名同学的作业,我们一起来看看这个同学做得对不对。
教师展示学生的作业:
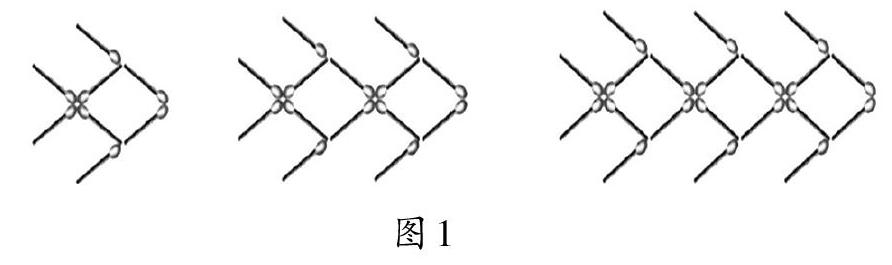
如图1,搭一条小鱼需要8根火柴棒,每多搭1条小鱼要增加6根火柴棒。如果搭n条小鱼所需火柴棒的根数为S,那么,可以看出,随着所搭小鱼条数n的变化,所需火柴棒的根数S是变化的;当所搭小鱼条数n确定时,所需火柴棒的根数S也是确定的。
师:他写得是否正确?
生5:正确。
师:在这个变化过程中,有几个变量?分别是哪几个变量?
生6:在这个变化过程中有两个变量,分别是小鱼的条数和火柴的根数。
师:你会用等式表示两者之间的联系吗?
生7:S=8+6(n-1)=6n+2。
师:当n取1、2、3时,你知道对应S的值吗?S的值唯一吗?
生8:当n取1时,S的值为8;n=2时,S=14;n=3时,S=20。S的值唯一。
生9:当n固定的时候,S的值才唯一。(这里“有疑”。)
师:补充得非常好,数学表述时要严谨,这样才不会有歧义。(这里有“高度”,从学科教学走向学科育人。)
师:在这个变化过程中,有两个变量S和n,当n变化的时候,S的值变化吗?
生10:变化。
师:当n确定的时候,S的值怎么样?
生11:确定。
师:也就是说,在这个变化过程中,有两个变量S和n,S随着n的变化而变化;对于变量n的每一个值,变量S都有唯一的值与它对应。
师:在作业本上还有一道题目。(幻灯片展示。)
教师展示学生的作业:|a|=1,a=。
师:这名同学是这样完成的,同学们,你们觉得正确吗?
生12:不对。
生13:应该是a=±1。
师:为了帮助他改正错误,我们可以帮他列一张表格,已知|y|=x,则:
生14:y分别是±2、±3、±5.5。
师:在这个变化过程中,有几个变量?
生15:两个变量,分别是x和y。
师:哪个变量随着哪个变量的变化而变化?
生16:变量y随着变量x的变化而变化。
师:对于变量x的每一个值,变量y有几个值与它对应?
生17:对于变量x的每一个值,变量y有两个值与它对应。
师:y值是不唯一的。
师:同学们,回顾刚才的几个变化过程,你能找到它们的相同之处和不同之处吗?
生18:都有两个变量。
生19:前两个变化过程中,一个变量的值确定后,另一个变量的值唯一确定,但最后一个变化过程中,y的值不唯一。
师:我们今天研究学习的是“唯一确定的”这种情况——函数。一般地,对于一个变化过程中的两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量。
2. 小结和拓展。
师:今天我们用数学的眼光看清了一些特殊的“变化”与“联系”,用智慧的钥匙打开了“函数”的新世界,你从中学到了什么?
生20:生活中有很多函数的例子。
生21:一个变化过程中如果有两个变量x和y,对于变量x的每一个值,变量y都有唯一的值与它对应,那么y是x的函数。
生22:x是自变量。
生23:函数可以用等式表示,也可以用图形表示,还可以用文字表述。
生24:函数一定得符合“唯一的值与之对应”。
师:同学们都说得特别棒!我们身边处处是数学,本节课我们在生活的实例中感受到了“函数”,然后在数学问题中加深了对“函数”的认识,再回归生活,用“函数”思想审视了生活。
随后,教师展示拓展微课和数学阅读材料,以增加学生的兴趣,让学生从传统的学习方式转变到多元化的学习模式,提高学生知识面的“长度”“宽度”“高度”。
二、教学反思
1. 好的数学课堂,要有趣。
一堂数学课从教学设计开始,就要抓住“有趣”,體现教学内容的价值所在,将数学生活化,让学生感受到生活中处处有数学。
好的数学课堂要具有挑战性,激发学生的兴趣,让学生有研究的意愿,维持学生的兴趣;教学方式多元化、形式多样化,让学生不仅会解题,还可以表达数学思想方法,说出解题过程、理论依据等,让学生的思维具有逻辑性、更严谨,思考更全面。在课堂的展现形式上,教师可以利用微课、短视频、幻灯片等,从传统的“空洞地说”到图片、影音的动态展示,突破重难点,给学生多维的感受,此外,还可以穿插与教学内容相关的数学阅读材料,扩大学生的知识面。
2. 好的数学课堂,要有“度”。
从情感层面来讲,数学课堂要有温度。有温度的课堂会让学生如沐春风。在这样的课堂上,教师平等待人、尊重学生,会让学生感觉很温暖。教师积极的情绪能够带动学生更好地学习和挖掘自身的力量,激发学生的学习兴趣,从而达到事半功倍的效果。
从知识层面来讲,数学课堂要有长度、宽度和高度。
长度:帮助学生纵观知识生长线,串联小学、初中、高中的知识,让学生了解知识不是独立的,而是循序渐进的,但与系统又是相辅相成的。有长度的数学课,可以激发学生继续学习的动力,也是学生自主探究的源泉,让学生知道学无止境。
宽度:教学内容不单单是教材上的定义、定理,还要有应用,包括对教材各种形式的解读与做题。在数学课堂上的实际应用不单单是就题讲题,还要进行学科知识的拓展、变化、变式、补充,让学生发散思维,学会看一知三,由已知条件能联想到相关的知识点,并从中找出与结论相关联的知识,构架出解题需要的知识框架。
高度:授之以鱼,不如授之以渔。课堂上不仅要传授给学生知识,还要传授其方法技能。教师讲解题目时,不仅要让学生知其然,更要让学生知其所以然。我们要从学科教学走向学科育人,将数学方法融会贯通到生活中,教学生用数学的眼光看世界。
3.好的数学课堂,要有“动”。
从显性层面来看,课堂上要让学生做到手动、耳动、眼动。数学作为基础学科,有一定的枯燥性。让学生动起来,有助于其更好地参与课堂,自主探索新知,拓展思维。手动包括动手度量、画图、计算、完成题目等;耳动以听讲为主,结合眼动,关注教师讲解、学生之间的合作等。课堂上也需要口动,即表达,比如回答问题、提问、对数学概念定理的表述等,这些也是学生认知的表现形式。
从隐性层面来看,课堂上要让学生做到脑动,让学生的思维动起来。脑动即在学习过程中在头脑中完成思考过程,根据已学知识思考与此问题相关的拓展应用。学习的过程尤其是数学学习的过程就是思考的过程。
4.好的数学课堂,要有“疑”。
“学贵有疑。”思维动起来,便会产生疑问。学习在初始阶段以“模仿学习”为主。在数学教学的过程中,教师设置情景,引导学生从生活中发现数学问题,从而提出数学问题。这个提出问题的过程即为“有疑”的过程。随后解决问题,从而达到对知识的认知和积累。
就本节课来看,函数是初中数学重要的知识点,是学生新接触的一个领域。函数的重要性决定了学好函数的必要性。由于初中生刚接触函数概念,新内容对他们来说,无疑是一个坎,跨过去便能开辟新的世界。笔者在设计的时候,从“有趣”出发,将教学形式多样化,呈现方式多元化,帮助学生打开新世界的大门;情境导入从生活出发,让学生学会用数学的眼光看世界,用数学的思维思考问题,做到学科上、生活上有“度”;贴近生活,用显性的动带动隐形的动,让思维不断活跃、思想不断成长;“有动”之后才会“有疑”,“有疑”便会探究,从课堂上的学习到课后的思考交流,学习氛围更浓郁了,班级文化更科学了,学生处处可以学习,“学而不思则罔,思而不学则殆”,从而达到学而思的结合。
