一种面向跨项目软件缺陷预测的特征过滤与实例迁移框架

刁旭炀，刘晓阳，徐 利，陈天群，徐亚周

(1.上海机电工程研究所，上海 201109； 2.上海航天电子技术研究所，上海 201109)

0 引 言

规模庞大和复杂的软件容易产生缺陷，从而导致整个系统在运行时产生错误、失效甚至崩溃，越晚发现软件缺陷则修复成本就越高。对于一个严重的缺陷来说，如果在软件发布之后才定位识别出来，那么其带来的修复代价往往是在需求和设计阶段的几十甚至几百倍，这对于企业来说是不可估量的经济损失。而对于一个架构复杂的软件，组织人员进行代码测试和审查需要耗费大量的人力物力资源，通常无法高效地发现软件缺陷。因此，如果能挖掘软件项目中的历史数据，设计出相关典型的度量特征，对软件中的程序模块进行缺陷倾向性预测，就可根据预测结果对缺陷倾向度高的程序模块进行重点测试与维护，从而有效地提高软件质量保障的效率。软件缺陷预测技术[1]正是从软件项目中去挖掘有效信息并设计缺陷度量特征，运用相关机器学习算法建立可靠的缺陷预测模型，来识别定位新程序模块的潜在缺陷。

按照源项目与目标项目是否同源，软件缺陷预测可分为源项目与目标项目同源的同项目软件缺陷预测[2-4](Within-Project Defect Prediction, WPDP)和源项目与目标项目不同源的跨项目软件缺陷预测[5-6](Cross-Project Defect Prediction, CPDP)。同项目软件缺陷预测通常运用于一个已经过多轮迭代开发的项目，此时历史项目版本中可供提取的实例集合足以支撑缺陷预测的建模。而在软件项目建立的初期，往往缺少带有缺陷标注的程序模块数据集来作为缺陷预测模型的训练输入，如何运用其他项目中已有的标注数据集对该项目进行缺陷建模与预测是跨项目软件缺陷预测的核心研究内容。

通常而言，2个不同的项目之间存在数据跨域问题，其特征与实例的分布差异性会导致缺陷预测模型性能的下降。为了尽可能缩小跨域项目间特征与实例的分布差异，本文提出一种面向跨项目软件缺陷预测的特征过滤与实例迁移框架KCF-KMM(K-medoids Cluster Filtering-Kernel Mean Matching)。具体来说，在特征过滤阶段，该框架采用基于K-medoids[7]的特征过滤算法，首先依据特征间的相似度计算方法对特征进行聚簇，然后从各个簇中筛选出与目标项目分布相似度高的特征，形成后续建模的特征子集；在实例迁移阶段，采用KMM[8]算法，首先将源项目与目标项目的实例数据集映射到同一空间内，然后计算2组数据集间的最大平均差异，并以此为依据分配源项目实例的训练权重；最后在建立预测模型的阶段，嵌入少量的目标有标注数据集来提升模型的预测性能。

1 相关工作

在基于特征迁移的方法中，Liu等人[9]在TCA[10]方法的基础上提出了一种基于自适应策略的特征降维提取方法TCA+；Zhang等人[11]基于log、rank、Box-Cox、均方根等常用特征变换方法，提出了一种MT的多重度量元转换方法，缩减源项目特征与目标特征间的差异；此外，Wu等人[12]采用自动编码器方法从原始特征中学习提取隐藏特征来缩减2个项目间的特征差异。在基于实例迁移的跨项目缺陷预测研究中，NNfilter方法直接基于目标实例对源项目实例进行最近邻筛选；TN方法将朴素贝叶斯模型运用到迁移学习中，以此对源项目实例的训练权重进行合理调整[13]；Sun等人[6]提出了一种基于协作过滤的源项目选择方法CFPS，该方法采用基于用户的协同过滤算法为给定的目标项目推荐合适的源项目。

通过上述的研究可知，特征迁移和实例迁移都能促进跨域缺陷预测模型性能的提升。因此，为了充分利用两者的优势，本文构建一种基于特征过滤与实例迁移的2阶段跨项目软件缺陷预测框架KCF-KMM。

2 KCF-KMM总体架构

本章对跨项目软件缺陷预测框架KCF-KMM进行了详细阐述，该框架主要分为特征过滤、实例迁移和模型训练3个阶段。图1展示了KCF-KMM的总体架构。

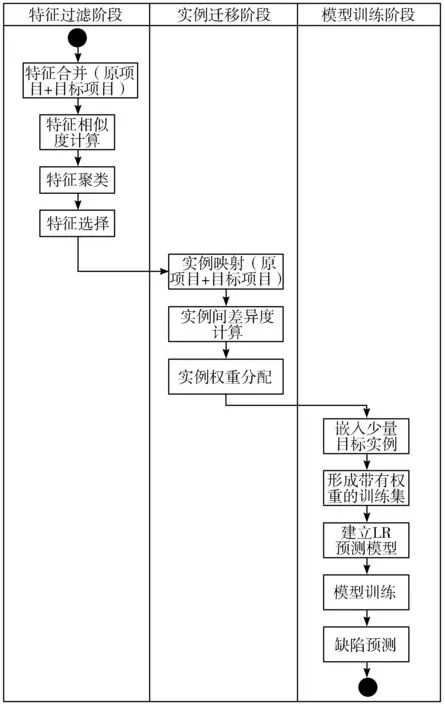
图1 KCF-KMM总体架构

在特征过滤阶段，KCF-KMM采用基于K-medoids的特征过滤方法，筛选出与目标项目集分布相似度高的特征子集；在实例迁移阶段，KCF-KMM采用KMM算法，将源项目和目标项目实例映射到同一空间内，衡量两者的差异度，依据与目标项目实例的相似程度分配训练权重。最后在模型训练阶段，嵌入少量目标项目的有标签数据，运用逻辑回归分类器进行建模、训练与预测。

2.1 特征过滤阶段

在特征过滤阶段，采用了基于K-medoids的特征过滤算法，筛选出与目标特征关联度高的特征子集。特征过滤阶段可进一步拆分为3个核心子阶段：基于信息熵增益的特征相似度计算阶段、基于K-medoids聚类算法的特征聚类阶段和基于特征聚类簇的特征选择阶段。

2.1.1 特征相似度计算阶段

在特征相似度计算阶段，首先合并源项目和目标项目的特征集合，并计算特征之间的关联度。由于2个项目集的特征之间的关联性不一定满足线性关系，并且前期的研究表明[14-15]，对于软件特征的度量，非线性的相关度度量方法要优于线性方法，因此本文采用基于信息熵增益[16]的方法计算特征fi与特征fj之间相似度。

在已知特征y为fj时，特征x为fi的后验概率，即信息增益率IG(fi│fj)如下：

IG(fi│fj)=H(fi)+∑y∈fjp(y)∑x∈fip(x|y)log2p(x|y)

(1)

其中，H(fi)的计算表达式如下:

H(fi)=-∑x∈fip(x)log2p(x)

(2)

基于特征fi、特征fj以及两者的信息增益 IG(fi│fj)，本文采用非线性的对称不确定性(Symmetric Uncertainty， SU)作为KCF-KMM框架的特征相似度度量公式，其计算公式如式(3)：

(3)

其中，特征fi和特征fj的SU值越高，表明两者之间的关联性越强，SU(fi,fj)最小值为0，最大值为1。SU(fi,fj)=0表示2个特征相互独立；反之，当SU(fi,fj)=1时，两者之间则是完全相关。

2.1.2 特征聚类阶段

在特征聚类阶段，借助K-medoids聚类算法将软件缺陷特征划分为不同的簇。相比于K-means算法，该算法的优势在于在更新簇中心时，不必重复计算各个特征之间的相关度，只需利用在特征相似度计算阶段预存的计算结果就可进行簇中心更新运行，不仅能有效提高算法的运算性能，而且也在有限的计算资源中节省了开销。

首先，根据K-S(Kolmogorov-Smirnov)检验计算每一特征在源项目和目标项目上的分布相似度。K-S检验[17]主要用来比较2个数据集的分布是否相同，其假设检验表达式如下：

H0:2组特征样本的分布相同

(4)

H1:2组特征样本的分布不同

(5)

对于某同一特征，假设在源项目SP中的特征维度为n和在目标项目TP中的特征维度为m，则SP和TP这2个样本集合分别为{SP1,…,SPn}，{TP1,…,TPm}。

对特征fi的K-S检验的步骤如下：

1)计算源项目集合与目标项目集合的经验分布函数Fcdf-SP和Fcdf-TP。

2)将SP和TP中的特征集合进行合并，然后进行综合排序，排序结果为{s1,…,sb,…,sn+m}。

3)分别计算sb在SP样本集合和TP样本集合中的观测概率Fobs-SP(sb)、Fobs-TP(sb)。对于某一样本点x在样本集合a中的观测概率Fobs-a(x)计算公式如式(6)所示。其中，z为样本a中的数量，t为样本a中小于等于x的数量，a为SP或TP。

(6)

4)计算fi在SP和TP间的特征分布相似度KS(fi)，其计算公式如式(7)所示，其取值范围为[0,+∞)。

KS(fi)=max|Fcdf-a(x)-Fobs-a(x)|

(7)

然后根据KS(fi)指标，由低到高排序选择前k个缺陷特征作为初始特征簇的中心。接着在预先计算好的特征间相似度列表中，查找其余特征与这k个簇中心的相似度，依次将剩余每一个特征放入与之相似度最高的簇中，并重新计算簇中心，更新各个簇中的特征子集，直到本次簇中心与上一次的结果一致为止。

2.1.3 特征选择阶段

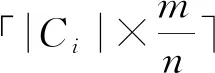
算法1给出了基于K-medoids特征过滤算法的详细描述。算法1的输入为源项目、目标项目、特征簇个数、初始特征个数以及筛选后的特征个数；输出则为筛选后的特征子集。

算法1 基于K-medoids的特征过滤

输入:

SP：源项目

TP：目标项目

k：特征簇个数

n：初始特征个数

m：筛选后的特征个数

输出:

FS：筛选后的特征子集

1.移除SP和TP的类标签；

2.将SP和TP合并形成特征集合F={f1,f2,…,fn}；

3.计算SU(fi,fj)；

4.计算同一特征在SP与TP上的分布相似度KS(fi)；

5.基于SU(fi,fj)和KS(fi)指标，利用K-medoids聚类方法将所有特征分成k个簇；

6.对每一簇中的特征fi按照KS(fi)计算结果进行升序排列；

8.将过滤后的特征放入FS中；

9.Return FS。

2.2 实例迁移阶段

在实例迁移阶段，采用的是KMM算法，通过比较源项目与目标项目实例间的平均分布差异来合理分配训练实例的权重。与其他基于实例的迁移算法不同的是，KMM算法无需事先利用2个项目的类标签信息预先建立类概率分布函数，而是以非参数的方式通过特征空间中的源项目集和目标项目集之间的分布匹配度直接推算源项目集的训练权重。考虑到源项目与目标项目实例的分布差异性通常情况下很大，该算法假设源项目条件概率Prs(y│x)与目标项目条件概率Prt(y│x)相等，从而将对Prs(x,y)和Prt(x,y)的衡量转化为对Prs(x)和Prt(x)的边缘分布概率的差异性比较。

KMM算法在将源项目与目标项目实例同时映射到RKHS[18]空间内的基础上，计算两者间的最大平均差异值MMD[19]，具体计算公式如式(8)：

(8)

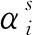
(9)

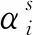
2.3 模型训练阶段

在该阶段，将目标项目中已存在的少量有标签数据集的训练权重设置为1，并与经KKM算法调整后带有权重的源项目数据集进行合并，形成混合训练集，运用LR(Logistic Regression)分类器构建缺陷预测模型，并对相关软件项目模块进行缺陷预测。

3 实验设计

3.1 实验数据集

本文以Apache下的15个公开Java项目作为实验数据集。所选取的实验数据集均可在Github(网址为https://github.com/klainfo/DefectData)上获取。针对Java面向对象程序语言的特点，Jureczko等人[20]已进行相关研究并提取出了20个典型的静态度量元，其中不仅含有通用软件缺陷特征，如软件规模、计算复杂度等，而且也包含了基于面向对象程序语言设计的相关缺陷度量元，如继承深度、不同域中的方法个数等。表1列举出了实验中项目数据集的相关信息，主要包括项目名称、版本号、程序模块数量(以代码文件为单位)以及总体缺陷率。

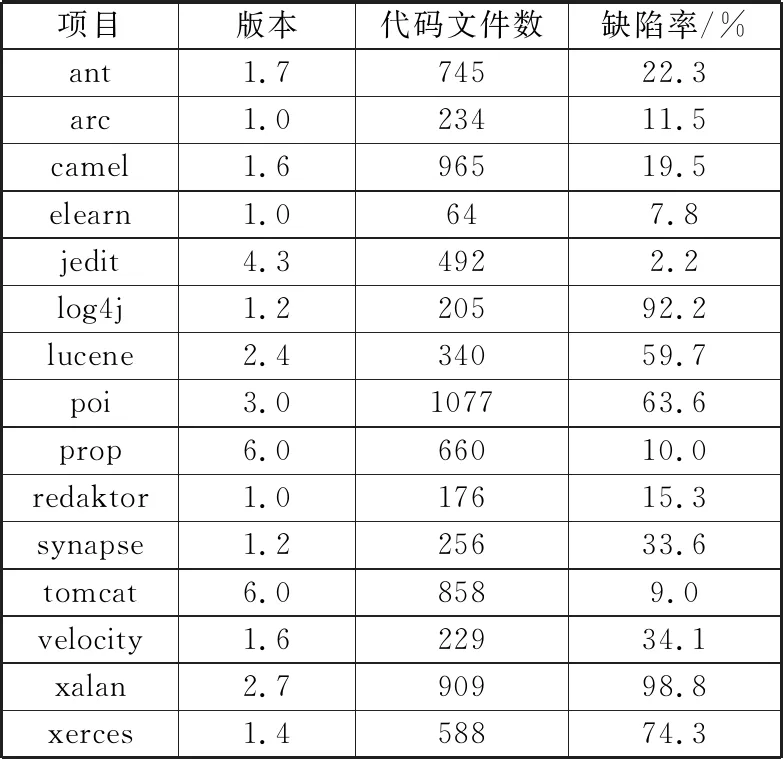
表1 Java项目数据集信息

3.2 实验环境与评价指标

3.2.1 实验环境

本次实验的硬件配置为一台带有Intel i7酷睿处理器、8 GB内存和GTX1060显卡的台式机，操作系统为Ubuntu16.04，使用的开发语言为Python及其相关科学计算与分析模块cvxopt和Scikit-learn，开发工具为jupyter notebook。

3.2.2 评价指标

本文以F1和Acc这2个维度对KCF-KMM框架的软件缺陷预测性能进行衡量。F1值综合了查准率和查全率，对预测框架的综合性能进行了考量，而Acc则是从总体预测精度出发，对框架的预测准确性进行了评价。两者的计算公式如下：

(10)

(11)

其中，P和R分别代表软件缺陷预测中的查准率和召回率，Nd→d+Nc→c表示预测结果正确的数量，Nd→d+Nd→c+Nc→d+Nc→c则是所有的预测结果。

4 结果分析和讨论

在实证研究阶段，将15个项目逐次作为源项目和目标项目，建立KCF-KMM缺陷预测模型框架，并进行跨项目软件缺陷预测。对于每一个目标项目，将其余14个项目作为源项目建立缺陷预测模型，考虑数据选择具有一定的随机性，采用m-折(m取20)交叉验证法并重复20次后，最终取所有预测模型结果的均值作为最终的评价指标。此外，本文通过SMOTE[21]过采样技术合成训练集中的少数类，使得有缺陷与无缺陷训练数据达到类平衡。

4.1 与经典的CPDP方法的差异性比较

为了说明KCF-KMM与经典CPDP方法之间的差异性，本文在Acc值上采用Friedman[22-24]和Nemenyi[25]检验方法。首先，采用Friedman方法对KCF-KMM与其他3个方法进行总体比较，如表2所示，p value的检验结果为1.43×10-9(远小于0.05)，该结果表明KCF-KMM与其他方法之间存在显著差异性。

表2 KCF-KMM与其他3种CPDP之间的Friedman检验

为了进一步分析KCF-KMM与3种经典方法的差异程度，采用Nemenyi检验方法来检验显著性差异。从表3的检验结果分析可得，KCM-KMM与TCA+和NNFilter显著性差异较大，与TNB方法比较相似。

表3 KCF-KMM与其他3种CPDP之间的Nemenyi检验

4.2 与基于特征迁移方法的性能比较

为了说明KCF-KMM框架相较于基于特征迁移方法的优越性，本文选取了具有典型代表意义的TCA+方法进行对比分析。表4和表5分别列出了KCF与基于特征迁移方法TCA+之间的Acc和F1对比结果。相较于TCA+方法，KCF-KMM在Acc的W/T/L和在F1值的W/T/L上，分别赢了15次和11次，该结果表明KCF-KMM比TCA+方法在整体上都有较大提升。与此同时，根据评价指标在15个项目上的平均值计算结果来看，KCF-KMM在Acc和F1值上分别比TCA+提升了34.1%和14.4%。综合上述比较结果，可判得KCF-KMM在缺陷预测模型的总体预测准确率和模型稳定性上都要优于只考虑特征迁移单阶段的方法。

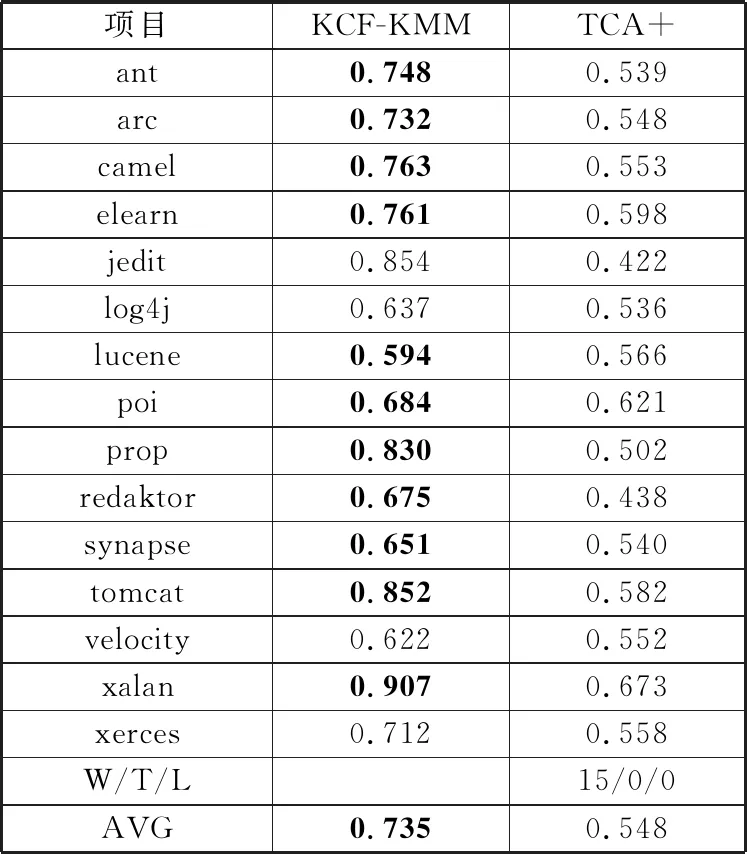
表4 KCF-KMM与基于特征迁移方法之间的Acc比较

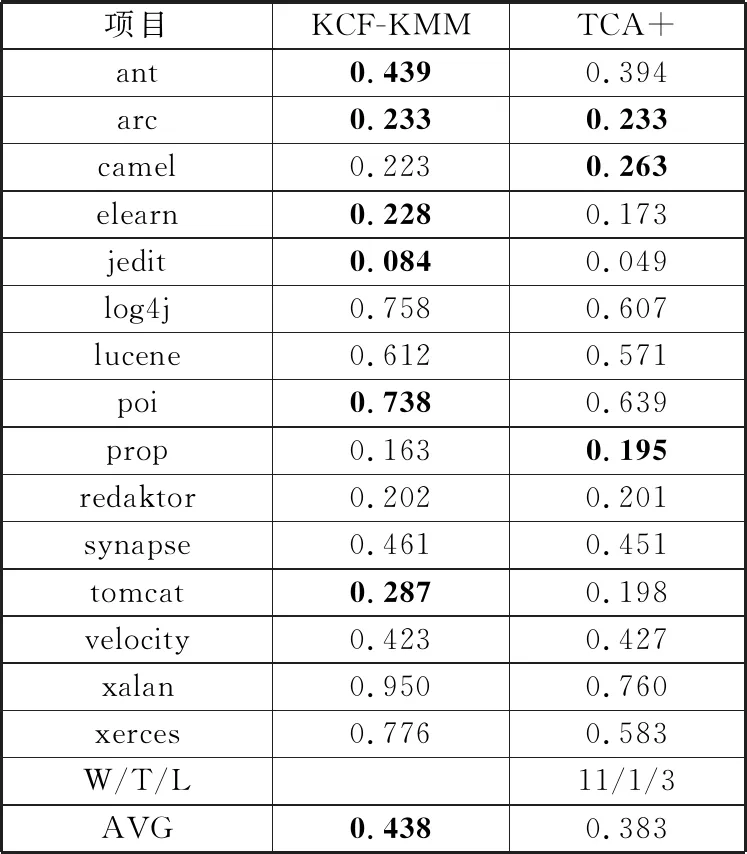
表5 KCF-KMM与基于特征迁移方法之间的F1比较

4.3 与基于实例迁移方法的性能比较

为了说明KCF-KMM框架相较于基于特征迁移方法的优越性，本文选取了具有典型代表意义的TNB和NNfilter方法进行对比分析。表6和表7分别列出了KCF-KMM与基于实例迁移方法之间的Acc和F1对比结果。KCF-KMM比TNB在Acc和F1值的W/T/L上都赢了超过半数，分别为11次和9次；相较于NNfilter，则分别赢了15次和10次。此外从预测评价指标的平均值来看，KCF-KMM在Acc上和F1值上也分别比TNB和NNfilter有所提升。综合以上比较结果，可判得在预测精度和模型稳定性2个方面，KCF-KMM都要比只进行实例迁移单阶段的CPDP方法来得更优。

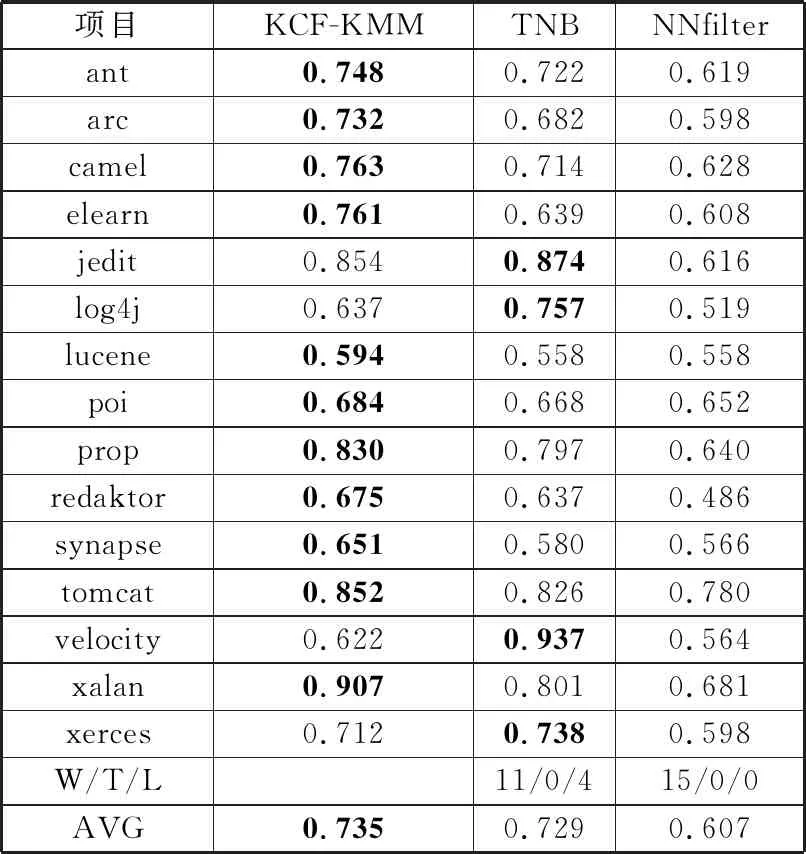
表6 KCF-KMM与基于实例迁移方法之间的Acc比较

表7 KCF-KMM与基于实例迁移方法之间的F1比较

基于上述分析，相较于经典的CPDP方法，KCF-KMM采用基于K-medoids的特征过滤方法筛选出了关键特征子集，并在此基础之上，运用KMM实例迁移相关方法对训练集权重进行调整，提高了与目标项目分布相似度高的数据训练权重。在经过上述特征过滤与实例迁移之后，整个软件缺陷预测模型的预测性能得到了很大的提升。

4.4 有效性影响因素分析

本节从外部和内部影响因素2个角度对缺陷预测模型的有效性进行分析。首先，从外部有效性来看，本文采用的数据集都是基于Apache下的公开Java项目，相关度量元数据集则是由相关专家设计，研究数据的可靠性和缺陷特征设计的代表性都得以保障；从内部有效性来看，本文所有的数据处理和算法设计都是基于Python相关的科学计算分析包进行编码实现，最大程度上保证了模型构建的正确性；且在评估指标上采用Acc和F1值，从多角度对缺陷预测模型的性能进行了验证，保证了验证结果的全面性和可靠性。

5 结束语

本文针对跨项目软件缺陷预测中特征关联与实例分布差异的问题，提出了一种面向跨项目软件缺陷预测的特征过滤与实例迁移框架KCF-KMM，筛选出来了与目标关联度高的特征，并合理分配了源项目实例的训练权重，提升了整个缺陷预测模型的性能。该框架仍有一些后续工作值得研究，具体来说:1)考虑其他特征相似性度量方法，并验证是否能提升预测性能；2)运用工程项目[26-27]的数据集来进一步验证模型框架在工程应用中的性能与效果。