基于迁移学习的卷积神经网络通道剪枝

冯敬翔

(华北计算技术研究所,北京 100083)

0 引 言

自2012年AlexNet在ILSVRC挑战赛中夺冠后，卷积神经网络(Convolutional Neural Network)在视觉领域的单目标检测、多分类识别、视频目标检测、图像分割[1]等领域受到广泛应用，此后其发展总体趋势向着网络层级更深、参数规模更大的方向行进。随着智能应用在边缘端部署需求的扩张，边缘设备存储空间、内存大小、运行功耗、实时性对于计算性能的限制，已经成为卷积神经网络在边缘端的实际部署瓶颈。为了能显著缩减模型占用的资源和计算开销，卷积神经网络压缩相关算法的需求变得日益迫切。

本文提出基于迁移学习方法来改进卷积神经网络稀疏化过程，探究针对基于BN层缩放因子的通道剪枝能否据此获得更高的剪枝阈值，对其剪枝效果与迭代收敛性进行研究验证，并从结构搜索的观点对实验结果进行解释。主要工作如下：

1)从多分类大数据集向小数据集实现迁移，对比加载预训练权重初始化重新训练、与冻结部分卷积层参数微调对稀疏化效果产生的影响。

2)对稀疏化后的通道按权重排序并剪枝，考察通道剪枝阈值选取容限，测试新形成网络结构的精度保持情况。

3)进一步地，利用迭代剪枝方法，探究模型精度保持极限与结构收敛性。从而证明，迁移学习更易实现充分的权值稀疏化，利于剪枝迭代快速趋近至该搜索空间的一个网络结构局部最优解。

1 相关工作

1.1 卷积神经网络剪枝

卷积神经网络强大的特征采样性能来自于大量的参数和复杂的多层结构，现代卷积神经网络也都多在经典结构上加深加宽来提高精度。如VGG[2]在AlexNet[3]的基础上，将层数从8层增加到19层；GoogLeNet[4]增加到22层，采用模块化(Inception结构)设计，并采用平均池化(average pooling)代替了全连接；ResNet[5]则通过使用多个有参层来学习输入输出之间的残差表示来取代一般输入，维持深度增加对于准确率的正收益，深度也从标准的152层甚至发展到上千层。

如图1所示，传统剪枝方法分为baseline训练、剪枝、微调3个步骤。从剪枝粒度上，可分为非结构化剪枝[6](unstructured pruning)和结构化剪枝(structured pruning)这2大类。非结构化剪枝即直接修剪单体权重(individual weights)，形成的权重矩阵是稀疏的，不易实现通用易部署的压缩和加速效果；结构化剪枝是针对卷积核(filter)[7]、通道(channel)[8-9]或是层(layer)[10]进行剪枝。卷积核剪枝工作方向上，文献[11]改进了基于卷积核权重排序进行剪枝的策略，采用卷积核的正则项L1绝对值之和作为剪枝权重；层剪枝需要对完整的层级进行裁剪，灵活性较差，精度风险较高，一般用于裁剪比较深的网络结构[12]；通道剪枝是当前结构化剪枝方法中，研究最多、工程应用最广的。其运行粒度较细，适合传统的机器学习框架，原模型结构保留较好。

图1 传统卷积神经网络剪枝过程示意图

1.2 剪枝与网络结构搜索研究

模型剪枝此前长期被认为是去掉神经网络中对推理预测结果贡献较低的参数，降低通道和神经元的数量，以达到缩减模型体积、降低存储计算成本的目的[13]。近年来随着相关领域理解加深，剪枝被重新认知为一种网络结构搜索[14](Neural Architecture Search, NAS)行为，即通过剪枝发现一个高效的网络结构，其针对目标数据集表现得更好[15]。相关推论来自于对一些剪枝后得到的模型结构初始化重训(train-from-scratch)，其效果未必比微调(finetune)后的结果差[11，14]。在引入了优化算法理论与流形学习(Manifold Learning)观点后，NAS工作方向得以扩充，不仅认为剪枝模型结构与参数确实存在解耦可能，同时探讨了剪枝同结构重训收敛速度差异与精度差异的产生原因[15-16]。文献[17]将差异主要因素归因为初始化引起的搜索方向收敛差异，并提出了迭代中权重多次初始化以纠正空间搜索趋向的方法；而文献[18]作为对前者的后续研究，提出权重采用掩模(mask)部分初始化可能取得更好的效果，以证明剪枝得到的mask结构本身具有一定的信息量，侧面支持了NAS观点的相关结论。此后工作则认为，剪枝结构再还原的性能差异可能来源于稀疏性(sparsity)、结构化与否、模型复杂度、学习率设定等多个维度的原因[19]，而后大量实验工作证明有一定稀疏度的结构化剪枝，其产生的结构重训是普遍可以还原精度的[20]。

2 基于迁移学习的BN层缩放通道剪枝策略

2.1 BN层缩放因子阈值通道剪枝

为了探究迁移学习是否对稀疏化工作存在正向影响，本文采用一种泛用性强、易复现的剪枝方案，即引入BN层(Batch Normalization)尺度因子作为通道裁剪依据。在每个通道中加入一个缩放因子，与通道输出相乘。统一初始化后，对BN层的缩放因子添加L1正则项，通过联合训练以实现因子稀疏化，然后在保证shortcut层级前后维度一致的前提下，按设定的阈值剪去缩放因子较小的通道。根据剪掉的通道，再统一剪去失去作用的卷积核并重构全连接层，以形成新的模型结构。

引入缩放因子并初始化、重训、阈值剪枝的流程如图2所示。

图2 BN通道剪枝过程中基于缩放因子筛选通道模型图

引入BN层通道因子后的损失函数如下：

(1)

其中，(x，y)代表训练数据和标签，W代表参数。前半部分是CNN原本的损失函数，后半部分是引入的惩罚项，λ是稀疏化因子用以平衡2项。

而BN层激活值的均值和方差计算如下：

(2)

(3)

则BN层输出的计算过程可以表示为：

(4)

(5)

其中的γ和β都是可以训练的BN层线性变换参数。选择因数项作为缩放因子则既可以保持缩放效果不会被卷积层简单学习直接恢复，又不过度影响模型结构。

2.2 基于迁移学习的模型稀疏化

前述引入g(γ)项的目的是在不影响L的可导性的前提下实现缩放因子稀疏化，g(γ)函数是缩放因子上的诱导惩罚项，通过使用形如下式的L1正则化：

(6)

缩放因子分布的稀疏性(sparsity)将直接影响剪枝阈值的确定，即决定了通道剪枝可剪容限与精度保存能力。引入L1正则项形式的惩罚因子后，BN层引入的尺度因子将根据惩罚系数λ值不同程度向0趋近，其分布形式也会因λ值的选择而不同。剪去缩放因子近似为0所对应的输出通道被认为对模型精度伤害较小，因此希望剪枝时有更多的缩放因子集中在0附近。图3为BN层缩放因子稀疏化前后、充分与否分布示意图。

图3 BN层缩放因子稀疏化前后、充分与否分布示意图

剪枝过程中发现，惩罚值λ依赖于人工选取，λ设置过小会使得稀疏化不充分而影响剪枝性能；λ过大会影响稀疏化后模型收敛与精度恢复。但是单纯的更换λ值对于稀疏化效果的提升终究有限，相关工作也表明，数据集与模型复杂度确定，参数一旦训练形成可能就存在稀疏化能力的上限[19]。故而，在此尝试利用迁移学习方法形成其本身就更适合稀疏化的权重。

同时使用迁移可能伴随着其他收益。在训练过程中，惩罚项不可避免地将对精度的收敛造成负面影响，直至后续训练过程将正则化效果迭代平衡。所以总体精度趋势会表现为先向下，后震荡，再回升至最终收敛。

本文在此尝试引入迁移训练，对模型稀疏化过程产生一系列正面影响：

1)精度起点更高。源模型的初始性能相对直接初始化重训好。

2)精度回升更充分。模型稀疏化前后对于精度的影响更小。

3)最终稀疏化程度高。稀疏训练收敛后缩放因子分布更向0集中。

实验方法基于由多分类的大数据集向单目标识别的小数据集迁移。对数据域D与任务T都不同的情况迁移存在一定风险，迁移方法根据迁移目标数据集与任务而异。

如图4，通过冻结源数据域(source domain)预训练模型的部分卷积层，训练剩下的卷积层与全连接层形成在目标数据域(target domain)新任务的识别能力。迁移所冻结的卷积层数量不仅取决于模型结构，还依赖于源数据域与目标域具体内容。如果冻结全部卷积层后模型效果不佳，尝试解锁更多的卷积层，或只使用预训练模型参数作为初始值直接进行重训。

图4 不同层级迁移方法网络各层参数处理示意图

为了保证迁移后微调(finetune)效果，在此同时使用warm-up策略对初期学习率进行调整，即初始学习率非常低，在前几个epoch内快速升高，然后在较长的迭代过程中逐渐下降。主要用于避免微调过程中初始学习率过大形成错误先验，造成提前过拟合现象，以保持分布平稳[21]。当使用梯度下降法以学习率η在源数据集训练k次时的权重变化情况为：

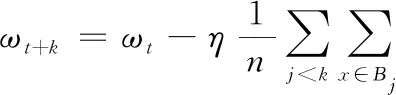
(7)

迁移后对于目标数据集进行微调权重更新为：

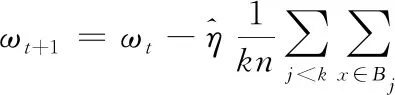
(8)

3 实验与分析

3.1 数据域介绍

源数据域选自COCO数据集，COCO数据集全称为Microsoft Common Objects in Context，最早由微软进行标注整理，是当前目标识别、检测等领域的一个较为权威可靠的多分类数据集，包含超过20万张图像。其中YOLOv3选用的80个类别当中有超过50万个目标标注，是最广泛公开的目标检测数据库，包括person、bicycle、bus、train、cat等。

目标数据域是Oxford的综合人手数据集，包含了4807张手部训练数图像和821张测试图像，总共标注了13000余个手部实例。每张图像标注了所有人类可感知到的所有手，单个手部实例超过1500平方像素以保证可检测训练。标注以矩形坐标边界形式记录，对人的姿势或可见度与环境因素没有任何限制[23]。

3.2 迭代剪枝结构搜索过程设计

基于前述网络结构搜索(NAS)工作方向的观点，本文对YOLOv3网络进行剪枝压缩，其过程如图5所示，本文将其描述为一类优化算法(Optimizer)过程。

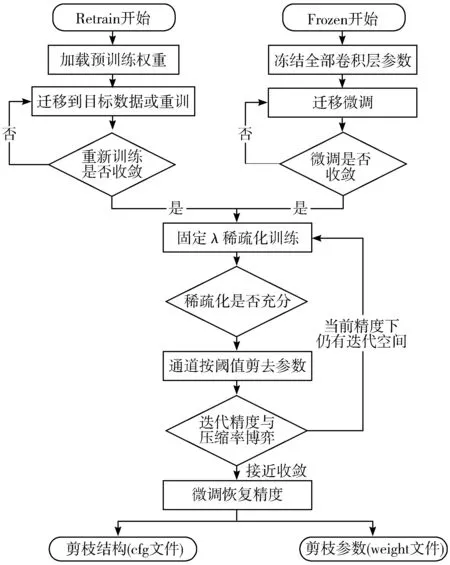
图5 引入迁移策略的网络空间结构局部最优解搜索过程

实验设计利用本文提出引入的迁移策略形成NAS过程的不同初始化，一次通道剪枝过程可视为寻优过程中的单次迭代，其迭代步长则直接由单次通道剪枝的阈值大小决定，即验证能否通过迁移并稀疏化形成不同的初始化状态，其在相同的迭代方向上是否可以收敛至一个相比直接训练剪枝潜能更好的局部最优(local optimal)结构。

3.3 实验结果

实验第一部分是比较使用2种迁移方案并测试稀疏化效果：1)加载yolov3.weight作为预训练权重，重新训练模型再进行稀疏化，模型记为Retrain。2)冻结来自COCO数据集的全部卷积层权重，根据其精度回升与收敛情况微调并稀疏化，模型记为Frozen。两者拟采用同样的稀疏化惩罚值λ，暂取λ=0.001。训练和稀疏化epoch=300，受设备限制batch size=8。

由表1可知，参数迁移程度比较高的Frozen方法对精度造成了轻微损害，但仍在可接受范围内。表2和表3给出了对Retrain方法不同阈值剪枝的测试结果。

表1 不同层级迁移方法稀疏化后精度保持情况

表2 λ=0.001下Retrain方法稀疏化后剪枝结果

实验中，Retrain方法在未经过微调时，要求剪去65%的参数时即已经发生了较大精度损害，阈值增大到70%时已经完全失去识别能力。据此认为当前λ=0.001的惩罚值已经不能对当前模型实现充分稀疏化；表3中，当增大稀疏化因子到λ=0.005时，剪枝阈值范围得以提高到较好水平：

表3 λ=0.005下Retrain方法稀疏化后较好剪枝结果

实验发现，后续即使再调整λ参数也很难在保持精度的同时再提高剪枝阈值，基本可以认为近似达到了当前方法对模型参数的剪枝能力上限。然后考察Frozen的剪枝性能。

从表4的结果观察到，Frozen方法模型可剪去的参数量非常大，即Frozen方法在λ=0.001下已经形成了非常强大的稀疏性，本文在保留网络层级连接性的前提下，避免剪掉通道最高阈值，剪去约97.1%的参数时仍能保持精度。

表4 λ=0.001下Frozen方法稀疏化后剪枝结果

3.4 迭代剪枝收敛性验证

实验第二部分将按照前述流程进行迭代剪枝性能验证。本文采用阈值0.8为步长进行剪枝迭代，并在第一次迭代后按λ=0.001的惩罚值稀疏化重训300 epoch，再做第二次阈值为0.8的剪枝迭代。

表5中第二次剪枝迭代之后出现了一定的精度损害。为了保证精度恢复到正常水平，在此进行了一次微调，放到原始数据中训练100 epoch使精度回升。此时相比单次阈值剪枝极限参数量(676万)又压缩了不到1%，此后再迭代有较大精度风险，而且在保留通道最高的阈值基础上已经很难继续压缩(再以较大精度损失仍可压缩不超过2%)，可以认为至此已经接近了迭代极限，且和单次剪枝收敛于近似同一个结构最优解。

表5 Frozen方法迭代剪枝各步骤实验结果

基于NAS过程观点，形成以下2个推论以解释其收敛过程：

1)在保持精度的前提下，迭代剪枝不能再轻易压缩参数量时，则可以证明当前剪型趋近于模型结构搜索空间中的一个局部结构最优解。

2)模型收敛于同样的局部最优解所需轮次越少，证明搜索起点与寻优方向越高效，即模型有效参量更少，稀疏化越充分。

至此，可以认定Frozen迁移方法确实能够形成强稀疏性，剪枝所形成的结构是对于这一数据集与任务域相对高效的结构。基于迁移方法的稀疏化策略大大提高了通道剪枝的可行阈值，提供了良好的结构搜索起点，使其可以更快地收敛于网络结构搜索空间中的一个局部最优解。

3.5 横向对比其他通道剪枝算法

在此，将本文利用迁移方法改进后的BN通道剪枝方法与2种针对YOLOv3的阈值通道剪枝策略进行对比。本文方法仍然记为Frozen。

第一种对设计shortcut的卷积层也进行了剪枝，剪枝采用每组shortcut中第一个卷积层的mask，使用5种mask实现5组shortcut相关卷积层剪枝，表6中记为Shortcut_mask；第二种用全局阈值筛选出各个卷积层的mask，再对mask取并集，归并后再进行剪枝，此方法相对激进，但在这个任务域上同样表现良好，不同剪枝阈值记为Shortcut_merge_0.9和Shortcut_merge_0.95。

表6 本文方法与其他阈值通道剪枝改进方法对比

可以看到本文使用迁移改进基础BN通道剪枝策略后，和一些针对性更强的剪枝方法相比依然有竞争力，在大体相当的精度范围内压缩率较为可观。

3.6 多数据集验证

在充分验证迁移方法对于Oxford手部图像数据集的权重稀疏化、剪枝阈值选取的改进效果后，本文用同样的方法对一些其他数据集进行剪枝调试，并开启混合精度来加速训练。

验证的数据集包括，VOC 2012目标检测数据集，包含11530张图片，来自20个分类；VisDrone无人机目标检测数据集，包含10209张静态图片，包含多个城市复杂环境在不同密度下的街景物体识别，检测难度较高。表7为验证结果。

表7 本文方法在其他数据集上验证结果

3.7 实验结果分析

本节针对实验结果成因进行分析。通道剪枝存在一个基本假设：BN层引入的缩放因子，能有效衡量通道输出对于最终识别精度的贡献度，剪去的参数是模型在目标数据上低贡献度的一种冗余(redundancy)，即卷积神经网络的过参数化[24]。迁移方法本身是利用源域与目标域之间的关联性，把源域学到的知识迁移到目标任务域或数据集[25]。实验从大而复杂的多分类数据集向小数据集迁移，所冻结的浅层权重是更加泛化(generalize)的轮廓、纹理特征采样，微调并重新形成全连接层时对其中一部分显然低相关的特征利用率较低，权重贡献相比重新训练集中得多。此后的稀疏化过程利用了这一特性，正则项更容易使大部分的低贡献特征受到惩罚并最终收敛到0附近，从而大大提升稀疏化效果，显著提高通道剪枝阈值，实现更高的压缩率。

4 结束语

在通道剪枝的研究方向上，本文尝试用改变网络结构搜索初始化策略的方式，区别于对其寻优迭代单步搜索优化的方案，以引导其收敛于一个更易于剥离网络中低效参数的局部最优解。本文通过向基于BN层缩放因子的通道剪枝引入迁移学习方法，并对比了不同层级迁移策略对通道剪枝压缩性能的影响。数据表明，本文方法在维持原模型精度在一定范围内的同时，实现了更高压缩率，并进一步针对剪枝结构搜索的收敛性与稀疏化性能进行了实验推证。

通道剪枝并非对于卷积神经网络部署优化的最终压缩手段，其压缩效果也并非完全符合实际嵌入式智能应用需求。本文的后续工作还包括但不仅限于：利用层剪枝方法压缩层级结构并降低推理开销，利用量化手段进一步压缩边缘端内存占用与存储体积等。