基于DT-CWT和SVM的踏面旋转不变纹理提取算法

赵聪慧，冯庆胜

(大连交通大学电气信息工程学院，辽宁 大连 116028)

0 引 言

随着现代化铁路技术的迅猛发展，高铁因其快速、便捷的特点成为备受大众青睐的出行方式，如何确保列车的安全性能成为铁路行业人员关注的焦点。车轮作为列车的重要组成部分[1]，其不仅承载着列车的所有重量，还承受着摩擦制动中的热负荷，它的状态决定了列车能否安全、平稳运行。踏面作为车轮与钢轨接触的载体，不可避免地会因为列车紧急制动或机车司机操作不当发生损伤[2]。为了避免列车事故，需要准确、有效地提取踏面的纹理信息[3]，以防患于未然。

常见的纹理提取方法包括：统计分析法(如灰度共生矩阵GLCM)、结构分析法(数学形态学法)、模型分析法(马尔科夫模型)和信号处理法(Radon变换、小波变换[4])4大类[5]。在已有的列车车轮踏面特征提取的研究中，主要采用灰度共生矩阵作为特征提取的手段。刘尚昆[6]、张志腾[7]用能量、对比度、熵、相关度4种统计量的平均值来表征灰度共生矩阵，以此描述踏面的纹理情况;杨颖等人[8]将灰度共生矩阵、灰度—梯度共生矩阵、标准方差三者组合，从中筛选出对纹理贡献最大的统计量。但是这些方法数据处理量大、数据处理过程繁杂，效率低下，对于一些旋转图像纹理信息[9]的提取存在较大的困难。同一个车轮，摄像机在不同的角度拍到的图像是不同的，人眼可以看出是同一个车轮，但是计算机却不具有这种识别能力。因此，需要一种可以提取旋转不变纹理信息[10-11]的算法。Liao等人[12]利用主成分分析(PCA)和双树复小波变换来检索数据库中的旋转信息，取得了较高的检索率，基于此，本文提出双树复小波变换[13]结合Radon变换来提取车轮的旋转不变[14-15]特征。

目前针对车轮的维护还停留在检修员使用手持设备或目测有无损伤，该方法效率低下、受主观因素大，容易产生误判。本文提出的基于图像的无接触检测方法检测速度较快、检测成本较低、检测精度较高、对车轮的损害小，日后可以广泛应用在列车车轮日常维护和车轮状态监测中。

1 旋转不变纹理提取

1.1 Radon变换

Radon变换是为了满足实际需求而将图像中的像素以一种其他形式表达出来的变换。二维图像f(x,y)的Radon变换[16]如式(1)：

(1)

由式(1)可以看出Radon变换是求函数在投影线上的投影值的过程，其本质是将不同角度的同一图像转变为图像在水平方向的平移。图1为带损伤的列车车轮踏面图像和旋转90°后的纹理图像，图2为Radon变换后的图像，可以看出旋转图像是原图像在水平方向的平移[17]。

图1 损伤踏面图像和旋转90°后的纹理图像

图2 Radon变换后的图像

1.2 双树复小波变换

双树复小波变换(DT-CWT)也叫二元树复小波变换，它是在传统离散小波变换[18]的基础上，以双树的形式进行变换得到的。双树复小波变换在二维图像的应用是通过4个实数抽样滤波器先后对图像的行和列进行滤波实现的[19]。图3所示为二维DT-CWT的二级分解结构。

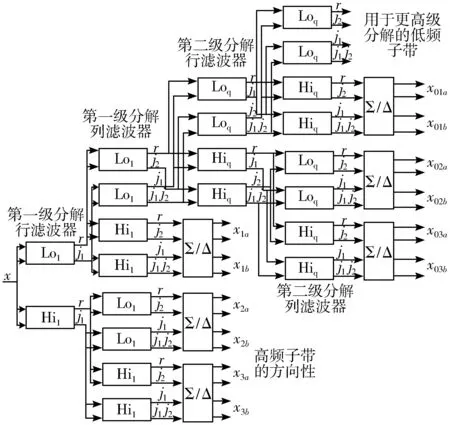
图3 二维DT-CWT的二级分解结构

图3中的x是输入的二维图像，Lo、Hi分别代表行、列滤波器，r代表滤波器输出的实部，j1、j2分别为行、列滤波器的虚部。DT-CWT在每一个尺度下分解生成2个低频小波系数和6个方向的高频小波系数(分别代表±15°、±45°、±75°)。

和传统的二维离散小波变换相比，DT-CWT变换体现出了平移不变、方向选择丰富、数据冗余度低及运算量小等优势，可以更有效地表征车轮踏面图像的纹理特征。图4给出了2种小波函数的对比图。其中，图4(a)是二维离散小波基，分解后得到图像在水平、垂直、对角3个方向的细节系数；图4(b)是二维双树复小波基，它分解后可以得到6个方向的细节系数。由此可见，二维双树复小波变换提取的图像纹理信息比离散小波变换更多一些，这与实际纹理所具备的丰富方向性很符合。因此使用双树复小波变换提取图像中的旋转纹理特征是合适的。

(a) 二维离散小波基

1.3 旋转不变纹理提取

本文采用Feraidooni等人[20]使用的纹理特征提取方法即小波系数模的均值和标准方差作为图像的纹理信息，均值和标准方差的计算公式如下[21]：

均值：

(2)

标准方差：

(3)

其中，μk是第k层子带系数的均值、σk是第k层子带系数的标准方差，fk(i,j)是每一尺度分解得到的低频或高频子带系数，M×N是分解的小波子带的大小。

首先，将24位真彩色图像转变为8位灰度图像并对灰度图像进行Radon变换；然后，利用DT-CWT分解图像；最后，提取各层的低频小波系数和高频小波系数，由小波系数模的均值和标准方差组成分类特征向量。对于一幅图像的低频通道，分解后得到一个8维特征向量(μ1,μ2,μ3,μ4,σ1,σ2,σ3,σ4)；对于高频通道，最终得到一个48维的特征向量(μ11,μ12,…,μ45,μ46,σ11,σ12,…,σ45,σ46)；将二者组合成56维的综合特征向量。图5为旋转不变纹理提取流程。

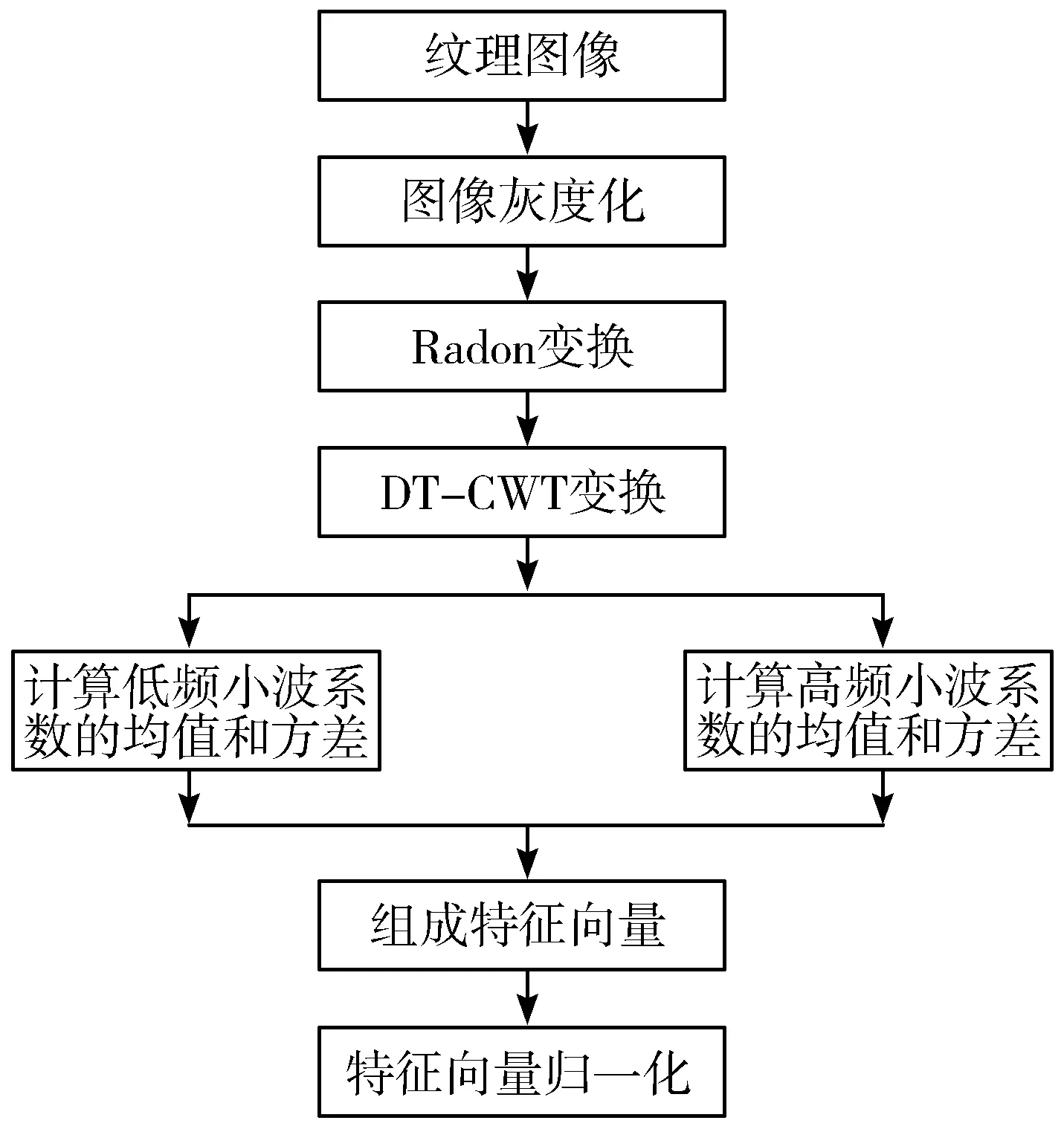
图5 旋转不变纹理提取流程

2 基于支持向量机的纹理分类

2.1 支持向量机SVM

SVM是一种以监督学习的方式对数据进行二分类的线性分类器。将2类数据分开的线性函数称为超平面。SVM的目的是寻找一个最优分类函数(最优分类平面)，使其可以无错误地识别2类数据，并使2个类别数据间的距离最远[22]。图6为线性可分SVM示意图，其中d是分类间隔，2类数据集中距离超平面最近的数据点称为支持向量。

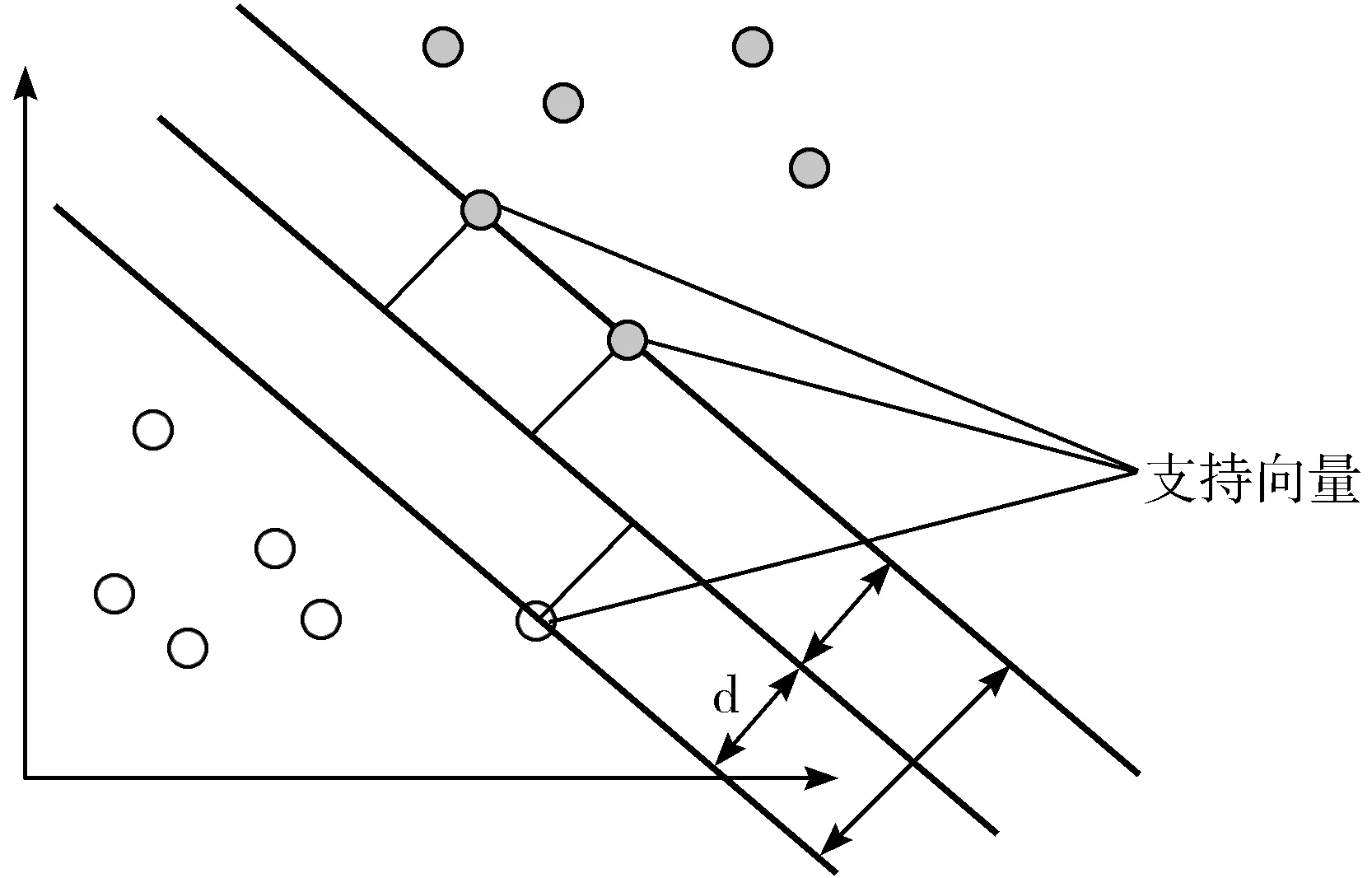
图6 线性SVM

由图6可知，SVM的最优分类超平面是针对线性可分情况来说的，但是本文需要分类的训练集是线性不可分的。因此，引入N个非负变量即松弛变量ξ=(ξ1，ξ2，…，ξN)，其允许除掉错误分类后的最优分类平面，最小化问题如下：

(4)

其中，w∈Rn、b∈R，(w,b)定义了一个分割超平面，如式(5)：

w·x+b=0

(5)

C为惩罚因子，当C较小时，最优平面取得最大距离‖w‖；相反，C较大时，错误分类点的数目较小。为了使其线性可分，需要将其向高维转化，然后在此特征空间寻找最优分类平面。图7所示为数据映射的原理[23-24]，图7(a)为原始特征空间中非线性可分的2类数据，图7(b)为映射到高维空间后线性可分的2类数据。

图7 非线性SVM

设φ(x)为映射函数，将x映射到高维特征空间，最优分类函数为：

(6)

式中∂i为拉格朗日乘子,K(xi,x)为核函数,xi、yj为2类中的支持向量，b为根据训练样本确定的阈值。常见的核函数有多项式核函数(Polynomial)、二次核函数(Quadratic)和径向基函数(RBF)。核函数不同，支持向量机的分类准确度也不相同。如表1所示，本实验针对不同的核函数和不同的惩罚因子，采用DT-CWT变换对支持向量机的分类精度进行测试。从表格中可以看出，当核函数为径向基函数(RBF)、惩罚因子为1000时，SVM的分类精度最高，为95.9%，其平均分类精度为91.2%，远远高于多项式核函数(Polynomial)和二次核函数(Quadratic)。

表1 不同核函数不同惩罚因子下的分类准确率 单位：%

2.2 分类方法与流程

由于本文的研究对象是列车车轮踏面，分类只需要分为有缺陷和无缺陷2种情况，故采用二分类的SVM即可。本文用于实验的车轮踏面图像共2组，一组是采集的有损伤的车轮图像，另外一组是采集的无损伤的正常车轮图像。由于踏面上损伤的尺寸不尽相同，直接计算整个图像的特征无法准确定位损伤踏面及损伤所在位置。因此将车辆踏面图像分割为若干大小相等的子图像，分别提取每一个子图像的纹理特征。

训练阶段首先标记样本，只要子图像内存在损伤，即将该子图像标记为损伤子块，反之，标记为正常图像。计算每一个子图像的纹理特征，利用这些特征来进行SVM的训练和分类，最后计算分类正确率。

3 实验结果

3.1 旋转不变纹理图像

本文实验数据来源于国内某动车所采集设备，从中选取了50幅，部分训练数据和测试数据如图8所示。每幅图像原始大小为640×640像素。将其按照160×160像素大小顺时针进行裁剪，共生成8000幅图像。为了采集旋转不变纹理特征，将原始图像按照步长30°,从0°到360°进行旋转，并以图像中心为基准截取大小为160×160像素的图像。如图9所示，共生成600幅图像。每幅图像中取12个分割子图作为训练集，取9个旋转子图作为训练集。其余为测试集。总共有1050个训练数据，350个测试数据。

图8 部分训练数据和测试数据

图9 S1灰度图像旋转30°到120°结果图，步长30°

3.2 评价指标

为了评价纹理图像分类的效果，本文采用准确率作为评价标准，其定义如下：

准确率=正确分类样本数/测试样本总数

3.3 结果与分析

由2.1节可知，当采用径向基核函数(RBF)、惩罚因子取1000时，SVM分类器分类效果达到最佳。因此，下面的实验将基于此指标进行SVM分类实验。

3.3.1 分类层数和提取的特征对分类结果的影响

为了研究DT-CWT取不同的分解层数以及提取的纹理特征对列车车轮踏面损伤识别的影响，本文对同一组图像分别进行2、3、4、5层的DT-CWT分解。同时讨论低频小波系数、高频小波系数哪一个对图像的分类影响较大。具体实验结果见图10。

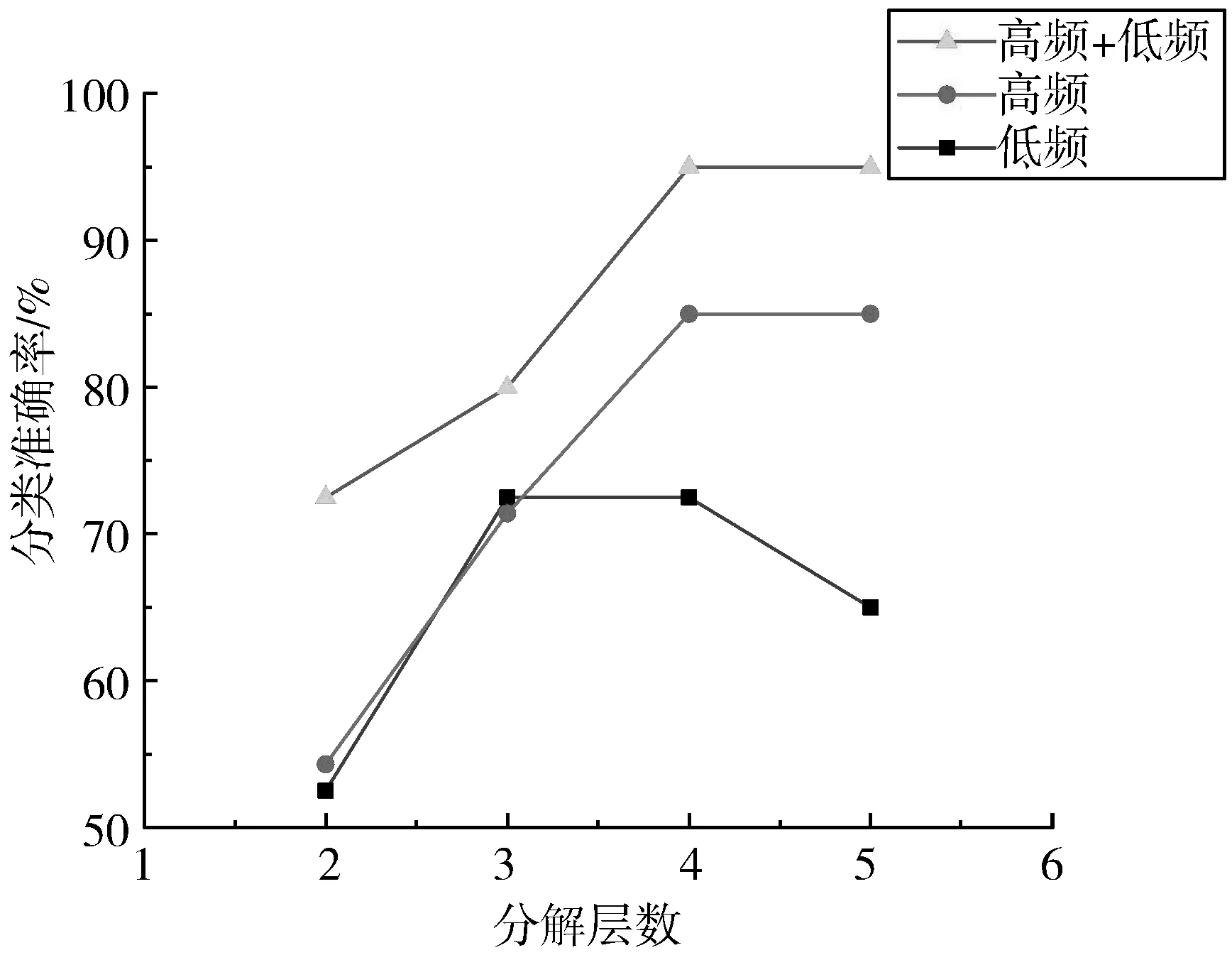
图10 不同分解层数、特征下的分类准确率

从图10可以看出，当DT-CWT分解层数为4层时，分类准确率最高。当分解层数大于4时，分类准确率维持不变或者降低。此外，可以看出采用DT-CWT分解出的低频+高频小波系数时，分类准确率要远高于单独使用低频或者高频，大约为95%左右，而单独使用低频特征只有65%左右。这说明DT-CWT分解的高频小波系数中含有丰富的纹理细节特征，而低频小波系数反映了纹理图像的整体特征。使用低频+高频小波系数，对DT-CWT做4层分解时，列车车轮踏面损伤识别效果达到最佳。

3.3.2 惩罚因子对分类准确率的影响

惩罚因子C体现了对错分样本的重视程度，C越大，对错分样本越重视，目标函数的损失越大。从图11中可以看出，随着惩罚因子的增大，使用灰度共生矩阵(GLCM)、二维离散小波变换、Radon结合DT-CWT这3种纹理特征提取方法的分类准确率呈现出一个先上升后稳定的趋势。分类准确率取最大值时，惩罚因子的值是最优的。相比于其他纹理特征提取算法，使用DT-CWT算法提取的纹理特征信息更丰富，SVM分类准确率更高，说明该算法更适合旋转不变纹理特征的提取。

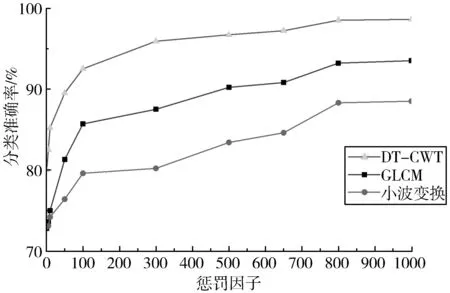
图11 不同惩罚因子下的不同算法的分类准确率

3.3.3 图像在加噪声后的分类准确率

由于现实中采集的车轮图像难免会受到外部环境的噪声干扰，而训练数据中又没有包含噪声的图像，因此，将实验数据中的所有图像都加上噪声以此来测试噪声对DT-CWT算法的影响。常见的噪声有高斯噪声、椒盐噪声。实验中，本文对椒盐噪声的噪声密度取0.05，高斯噪声的均值取0.1，标准方差取0.02进行实验。图12为S1分割后的子图像和加噪声后的图像。

图12 原图、加高斯噪声和椒盐噪声后的图

为了比较各种算法受噪声影响的程度，下面的实验取分类效果不是很好的惩罚因子C的值为1，这样才能使加噪声前后图像的分类结果有明显变化。使用径向基函数(RBF)作为SVM分类器的核函数，计算分类准确率。表2列出了不同算法在加噪声前后的分类准确率。

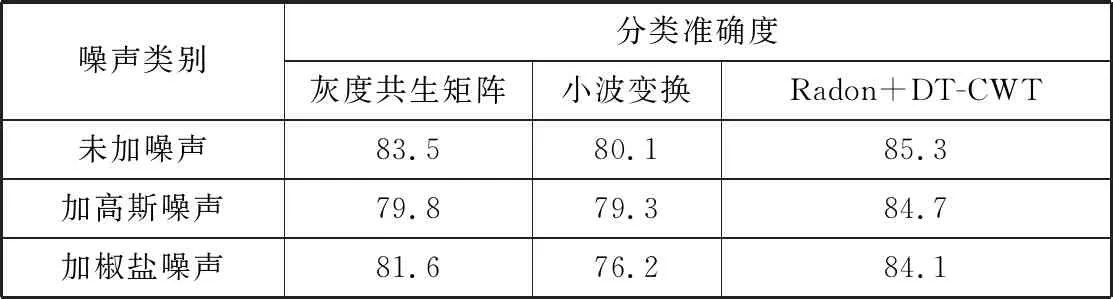
表2 不同算法在加噪声前后的分类准确率 单位：%

从表2中可以发现：对于高斯噪声，灰度共生矩阵算法受到的影响最大，分类准确率明显降低，小波变换次之，DT-CWT受到的影响最小；对于椒盐噪声，小波变换算法受到的影响最大，分类准确率明显降低，灰度共生矩阵次之，DT-CWT受到的影响最小。总的来说，DT-CWT分类准确率受噪声的影响较小，是提取踏面纹理特征较为理想的选择。

4 结束语

本文提出了一种利用Radon变换和双树复小波变换(DT-CWT)提取列车车轮踏面旋转不变的纹理特征的方法，使用SVM分类器进行分类，分类准确率较其他算法提高了5%左右。双树复小波变换平移不变、方向选择丰富、数据冗余度低及运算量小等优点使其能够较好地描述旋转纹理的特性；同时，SVM适用于数据集较少、非线性样本、高维度特征、抗噪声能力强的特点在本文实验中也得到了体现。日后可以将本文算法用于列车车轮状态的自动检测系统，为及时发现行车隐患防患于未然提供重要依据。