中国人力资本错配测度：区域差异及影响因素

杨仲山 谢黎

摘 要：本文利用柯布—道格拉斯（C-D）生产函数对2000—2017年中国30个省份的人力资本错配指数进行测度，从省级层面、区域层面考察了人力资本错配的类型和演进特征，通过泰尔指数对东中西三大地区和八大经济区人力资本错配的区域差异及来源进行揭示，通过空间计量模型检验了人力资本错配的空间关联及影响因素。研究结果表明：考察期内中国人力资本错配得到一定程度的缓解，整体上由配置过度演变为配置不足;人力资本错配的演进态势在不同省份和不同经济区具有显著差异;三大地区人力资本错配差异的主要来源为区域内差异，而区域间差异对八大经济区人力资本错配的区域差异贡献率趋于上升;整体上人力资本错配具有明显的空间关联特征，地方政府财政支出和产业结构调整加剧了人力资本错配，而居民消费水平和信息化程度的提升有助于缓解人力资本错配。

关键词：人力资本错配;区域差异;C-D生产函数;空间计量模型

中图分类号：F222;F240  文献标识码：A

文章编号：1000-176X（2021）11-0109-11

自Schultz[1]ADDINNE.Ref.{3B30A3F8-F55C-47FC-AF9A-A228CE246DD7}提出“人力资本”的概念以来，人力资本在学术研究和政策文件中被反复提及，成为新增长理论解释全球、地区及行业经济增长效率或质量差异的重要视角。改革开放四十余年来，中国宏观经济取得了全球瞩目的增长绩效，而人力资本累积所释放的“人口红利”是其重要且不可或缺的驱动因素[2]ADDINNE.Ref.{1D25C3C1-C7F3-409B-B813-CEC6AC8B6492}。中央财经大学中国人力资本研究中心发布的《中国人力资本报告（2019）》显示：2017年中国实际人力资本存量达到1 688.57万亿元，比2000年增长了3.03倍，年均增长8.55%。然而，与此相悖的是，刻画经济增长效率或发展质量的全要素生产率却未维持较高的增长态势，且人力资本对经济增长的贡献率也远低于发达经济体[3]ADDINNE.Ref.{81C8CD5A-AEDB-4401-9075-425028CDAB51}，一个重要的根源在于中国人力资本存在较为严重的错配而致使其配置效率低下[4]ADDINNE.Ref.{04F10C19-C01C-4486-BEF9-E763CB6DF157}。作为要素错配的一种，人力资本错配是相对最优配置而言的，表现为对人力资本最优或有效配置的偏离程度[5-6]ADDINNE.Ref.{1D25C3C1-C7F3-409B-B813-CEC6AC8B6492}。国家统计局公布的数据显示，中国的劳动人口数量已于2013年达到峰值，由此进入了较长时期的下降区间，中国的人口结构已呈现出典型的“老龄化”特征，中国经济也随之进入增速下滑的发展阶段。在人口“数量红利”趋于衰减的背景下，中国固然应该加大教育和医疗等公共服务投入力度，以最大限度地挖掘人口“质量红利”的增长潜力，但如果现存的人力资本错配或低效率配置得不到有效矫正，中国经济后续维持较长时期中高速增长的目标也难以达成[7-8]ADDINNE.Ref.{A6D7B459-0A08-4137-BD70-E309B6CBA35B}。尤其是当前中国正处于经济粗放型增长向高质量发展转型的关键历史窗口，更加强调全要素生产率增长的动力机制，这必然要求最大限度解决人力资本错配问题，以提升人力资本对经济高质量发展的驱动力。这就引申出一系列需要回应的现实问题：中国人力资本错配的状况如何？在时间演进和空间差异层面呈现出怎样的趋势特征？其背后的逻辑动因又是什么？诸如此类问题的回应无疑具有重要的学术价值和政策蕴含。

一、文献综述

对人力资本存量的科学估算是测度人力资本错配指数的前提条件。目前，学术界估算人力资本存量主要采用教育年限法、成本法和终生收入法（J-F收入法）。教育年限法是依据劳动者的平均受教育程度乘以劳动人口数量来估算人力资本存量[9]ADDINNE.Ref.{F2598268-F815-424B-87F7-D38D8A1510C9};成本法，也称教育经费投资法，是根据人力资本投资来测算人力资本存量，如为了提高劳动者的素质而花费在教育、培训和医疗等方面的投资;终生收入法由Fraumeni和JorgensonADDINNE.Ref.{9788D09B-BBEC-4018-97DE-0570DFCD84C4}提出，是用人力资本产生收入的现值来估算人力资本，即劳动者预期的未来收益的现值，实质是从当期来估计教育投资对受教育者一生收入的影响，并将此收入汇总得出受教育者的人力资本存量[10]。终身收入法的优点在于能更加准确合理地反映出教育和健康等长期投资对人力资本积累的重要作用，因而在国际上被广泛采用。

从人力资本错配的视角来讨论人力资本配置效率问题的相关研究仍较为缺乏，早期的研究主要关注劳动力要素的错配问题，并认为劳动力错配是引致全要素生产率（TFP）下降和总产出损失的重要原因[11]ADDINNE.Ref.{93A20A57-ABC7-447C-BF1A-B6C6B5C33F5B}。近几年来，人力资本错配或配置效率得到学界高度关注，其主要聚焦在人力资本错配的现实表征及其对经济效率损失的影响、人力资本错配的触发动因等方面。马颖等[12]ADDINNE.Ref.{0836BAA2-F88E-46B5-9821-989186237B1A}以企业两要素生产函数为基本设定，用人力资本实际使用数量与最优配置状态的比例来衡量人力资本错配，对三次产业的人力资本错配进行测度，发现第一产业和第三产业呈现出人力资本配置过度，而第二产业尤其是制造业表现为人力资本配置严重不足，人力资本错配使得2007年和2013年中国实际总产出分别損失1.79%和1.63%。葛晶和李勇[13]ADDINNE.Ref.{833F70B3-27BF-4DC8-ACB3-B1AB1F51BE95}将企业生产函数拓展为资本数量、劳动力数量和劳动力质量的三要素生产函数，测算了2009—2015年中国19个细分行业的人力资本错配，并从行政垄断视角阐释了人力资本错配的形成机制，行政垄断解释了人力资本错配在行业间差距的59.65%。

解晋[8]ADDINNE.Ref.{0C575DBE-7CEE-40DD-89A0-F6B1574931D2}采用 Aoki 模型和地区C-D生产函数的测度结果表明，中国人力资本错配呈现出东部地区比中西部地区严重的特征事实，市场化水平、基础设施建设和产业结构合理化有利于人力资本配置效率的改善，而地方政府的不当干预和金融发展加剧了人力资本错配。王宋涛等[14]ADDINNE.Ref.{BB87F993-66E3-4E05-93ED-14E90041741F}通过构建 “工资基尼系数”来衡量劳动力错配，发现要素市场分割程度越严重的地区，劳动力和资本流动的成本将会大幅提升，其资源错配程度也越严重。刘贯春等[15]ADDINNE.Ref.{C60B173E-0B7D-4312-A008-32440A1F1508}构建土地、劳动力和资本三种要素生产函数，测度了农业部门和非农业部门的人力资本等要素市场的扭曲程度，认为扭曲是导致区域经济非平衡发展的关键原因之一。杨志才[16]ADDINNE.Ref.{7551668E-DC34-4543-9263-B17D32588402}发现，人力资本等要素错配恶化了地区间收入差距，且加剧了收入差距对经济增长的阻碍作用。王启超等[17]ADDINNE.Ref.{1E4A337F-03D0-4F26-9CA0-2D2996C1981D}通过构建金融业与制造业人才最优配置比，发现在283个地级市样本中，有273个城市人力资本配置过度偏向金融业，这种“脱实向虚”的配置方向显著降低了制造业全要素生产率。李静和楠玉[18]ADDINNE.Ref.{1A3275BF-AB14-4184-AA97-05F3CB334E97}发现，人力资本错配与制度体制有一定关联，中国事业型单位、行业和部门以其高福利和稳定的收入预期吸引大量人力资本流入，进而造成人力资本错配和收入差距扩大，且对社会的消费增长和消费升级带来不利影响。

已有文献为本文提供了思路和方法等方面的借鉴或启示，但在以下方面仍有改进的空间。一是在人力资本错配指数测度中人力资本存量的估算上，已有研究主要采用教育年限法和成本法，这两种方法虽具有计算简单的优点，但误差大、代表性差、存在滞后性和片面性，其合理性和准确性遭到质疑。本文选择中央财经大学中国人力资本研究中心基于J-F收入法估算出来的各省份人力资本存量数据，对人力资本错配指数进行测度，在一定程度上提升了该指数估算的准确性。二是在研究对象上，已有文献更多地关注企业或行业的人力资本错配或配置效率问题，而对区域层面人力资本错配的研究较少，尤其缺乏对其时空演进特征和区域差异进行深入揭示的研究。三是研究方法上，大多数研究通常基于企业层面的微观数据和生产函数错配指数[5-13]ADDINNE.Ref.{1A3275BF-AB14-4184-AA97-05F3CB334E97}，少数研究采用“工资基尼系数”来刻画劳动力错配[14]ADDINNE.Ref.{1A3275BF-AB14-4184-AA97-05F3CB334E97}，以及基于行业人力资本强度差异测度不同行业的人力资本错配程度[19]ADDINNE.Ref.{1A3275BF-AB14-4184-AA97-05F3CB334E97}。由于Aoki模型放松了参数法中生产函数形式的约束，在人力资本等要素错配的测算中得到广泛应用，其不仅适合微观企业层面的要素错配研究，还为宏观区域层面提供了可靠的分析框架[20]ADDINNE.Ref.{1A3275BF-AB14-4184-AA97-05F3CB334E97}。在估計生产函数的弹性系数时，大部分研究采用普通最小二乘法（OLS），即假设每个截面都是一样的，这相对于直接给定固定产出弹性系数而言，提高了估算合理性，但并不能得到差异化的弹性系数。而最小二乘虚拟变量法（LSDV）可以给不同的样本不同的截距，并将每个截面通过截距项的差异分离出来，得到更符合现实的差异化弹性系数。由此，本文基于2000—2017年中国省级面板数据，着重考察物质资本和人力资本两种要素，选择假定规模报酬不变的柯布—道格拉斯（C-D）生产函数以及Aoki模型，并采用最小二乘虚拟变量法（LSDV）计算弹性系数。在对人力资本错配进行测度的基础上，综合采用核密度估计和泰尔指数分解等方法，深入阐释其时空演进及区域差异。

二、研究方法

（一）Aoki模型

测算地区层面上的人力资本错配首先要从要素的价格扭曲系数入手，本文借鉴陈永伟和胡伟民[21]ADDINNE.Ref.{76710BF4-DBC6-41B0-B6EA-056BE38F2209}的方法，通过测度物质资本错配指数τKi和人力资本错配指数τLi，来反映各地区物质资本和人力资本的错配情况。

γKi=1/1+τKi，γLi=1/1+τLi （1）

其中，γKi和γLi分别为物质资本投入和人力资本投入的价格绝对扭曲系数，表示投入要素价格没有扭曲时的加成情况，但实际测算时价格绝对扭曲系数难以观测，用价格相对扭曲系数Ki来代替：

Ki=Ki/K/siβKi/βK，Li=Li/L/siβLi/βL（2）

其中，Ki/K表示地区i使用的物质资本占物质资本总量的实际比值;si=Yi/Y表示地区i的产出Yi占整个经济体产出Y的份额;Li/L表示地区i使用的人力资本占人力资本总量的实际比值;siβKi和siβLi分别表示物质资本贡献值和人力资本贡献值;βK=∑Ni=1siβKi表示产出加权的物质资本贡献值;βL=∑Ni=1siβLi表示产出加权的人力资本贡献值;siβKi/βK表示地区i的物质资本错配程度; siβLi/βL表示地区i的人力资本错配程度，若该比值大于1，说明相对于整个经济体而言，该地区人力资本配置过度;若该比值小于1，则表示该地区人力资本配置不足。

进一步借鉴赵志耘等[22]的做法，选择假定规模报酬不变的C-D生产函数，即βKi+βLi=1， 估计各地区物质资本和人力资本的要素产出弹性βK和βL。对生产函数两边同时除以Lit后取自然对数，并在模型中加入地区虚拟变量μi和年份虚拟变量λt，用来控制各省份不随时间变化的个体特征和年份固定效应，整理可得式（3）：

lnYit/Lit=lnA+βKilnKit/Lit+μi+λt+εit（3）

借鉴白俊红和刘宇英[6]ADDINNE.Ref.{A1A3190D-FE67-46CB-AE48-B9A91A0B2874}运用LSDV计算中国30个省份的弹性系数βKi和βLi，代入生产函数计算人力资本错配指数，错配指数存在正负之分，其绝对值大小代表错配程度，人力资本错配指数τLi>0，表示人力资本配置不足，人力资本错配指数τLi<0，表示人力资本配置过度。

（二）核密度估计

核密度估计属于非参数估计，主要用于随机变量的概率密度估计，利用连续的密度曲线描述随机变量的分布形态。假设一组连续型随机变量X的密度函数为fx，在点x的概率密度的估计式为：

fx=1/Nh×∑Ni=1KXi/h-x/h（4）

其中， N为观测值的个数;h为带宽;K（·）为核函数;Xi为独立同分布的观测值;x为均值。选择高斯核函数对中国30个省份的人力资本错配指数演进动态进行估计。

（三）泰尔指数分解

测量差异的方法较多，包括变异系数、基尼系数和泰尔指数等。本文不仅度量人力资本错配的区域差异，还试图厘清人力资本错配差异的来源。泰尔指数具有按照子群分解差异的优点，可以将差异分解为组内差异和组间差异[23]ADDINNE.Ref.{1E6BAAFA-4C74-400E-8555-66DEB864BDA3}，故本文选用泰尔指数测度中国省级层面的人力资本错配差异。泰尔指数Theil的计算及分解方法如下所示：

Theil=1/n×∑ni=1τLi/μ×lnτLi/μ（5）

Theil=TheilW+TheilB（6）

TheilW=∑mk=1skTheilτLk（7）

TheilB=∑mk=1sklnμk/μ（8）

其中，n表示样本量; τLi表示人力资本错配指数，按绝对值由低到高排序后，第i个省份的人力错配指数的绝对值;μ表示所有省份人力错配指数绝对值的平均值;m表示组数;μk表示第k组样本平均人力错配指数绝对值;sk表示第k组样本人力资本错配指数绝对值得分占总体人力资本错配指数绝对值得分的比值;TheilW表示组内差异;TheilB表示组间差异。

三、人力资本错配的系统测度及演化态势

（一）变量选择及数据来源

1.产出变量

产出变量（Yit）用各省份的地区生产总值表示，为了剔除价格的影响，本文利用地区生产总值指数（2000年=100）对地区生产总值进行了处理，数据来源于2000—2017年《中国统计年鉴》。

2.人力资本投入量

人力资本投入量（Lit）用中央财经大学中国人力资本研究中心根据J-F收入法估算出来的各省份人力资本存量表示。为了剔除价格影响，本文利用消费者物价指数（2000年=100）对人力资本存量进行了处理。

3.物质资本投入量

物质资本投入量（Kit）用各省份物质资本存量表示，使用永续盘存法来计算，公式如下：

Kt=It/Pt+1-δtKt-1 （9）

其中，Kt表示当期固定资本存量;It表示当期名义固定资本形成额;Pt表示固定资产投资价格指数;δ表示折旧率，参考张军等[24]ADDINNE.Ref.{89AE8B1C-746A-4B1A-AC88-83C1168F8B1B}设定为9.6%;Kt-1表示上一期固定资本存量，数据来源于2000—2017年《中国统计年鉴》。

（二）人力资本存量的比较

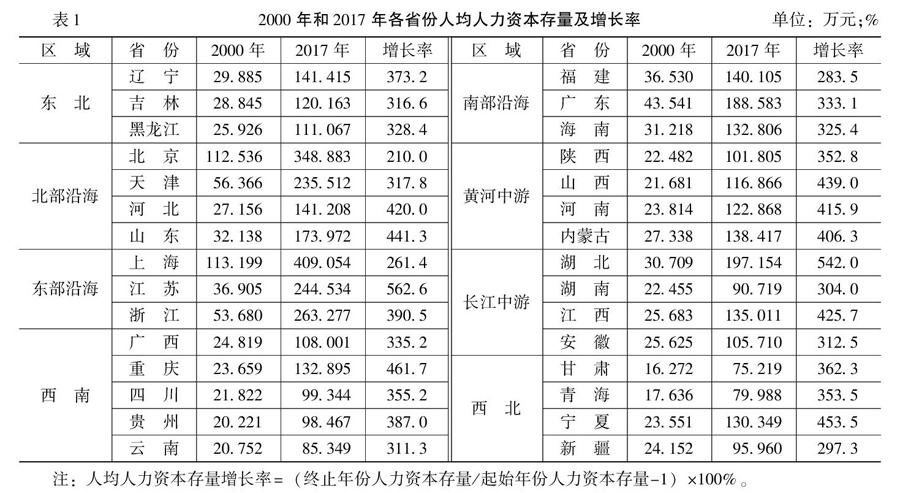
选择2000—2017年中國30个省份（不含西藏和港澳台地区）为样本，为了剔除价格影响，本文利用各省份消费者物价指数（2000年=100）对人均人力资本存量进行了处理，限于篇幅，仅将2000年和2017年各省份人均人力资本存量及样本期增长率的结果报告于表1。

从表1可以看出，2000年人均人力资本存量最高的省份，主要为东部沿海经济区的上海和浙江，北部沿海的北京和天津，南部沿海的广东，最低的主要集中在西北的甘肃和青海，西南的贵州和云南以及黄河中游的山西。2017年人均人力资本存量最高的省份，主要为东部沿海的上海、浙江和江苏，北部沿海的北京和天津，最低的主要集中在西北的甘肃、青海和新疆，西南的云南以及长江中游的湖南。由此可见，中国人均人力资本存量水平具有明显的梯度特征，沿海发达地区高于内陆欠发达地区，这一特征并未随着时间的推移发生实质性的改变。

就增长率来看，人均人力资本存量增长率最高的5个省份是东部沿海的江苏、长江中游的湖北、西南的重庆、西北的宁夏和北部沿海的山东，而人均人力资本存量增长率最低的5个省份是北部沿海的北京、东部沿海的上海、南部沿海的福建、西北的新疆和长江中游的湖南。这一发展态势说明，借助于西部大开发和中部崛起等国家区域发展战略的实施，长江中游、西南和西北经济区充分发挥后发优势聚集人才，部分省份的人均人力资本存量呈现出较高的增长态势，但整体而言，长江中游、西南和西北经济区内部大多数省份的人均人力资本存量增长率仍有待于进一步提高，人均人力资本存量仍然呈现典型的区域发展不平衡的特征事实。

（三）各省份及八大经济区人力资本错配的演化特征

基于中国30个省份的投入产出数据，根据式（1）—式（3）测度人力资本错配指数，限于篇幅，仅报告了2000年和2017年的结果，如表2所示。

从表2可以看出，各省份均存在人力资本错配或扭曲，2000年配置过度的省份有20个、配置不足的省份为10个，说明该年中国整体上人力资本配置过度较为严重，这一特征蕴含着人力资本供给相对于地区经济发展对人力资本的需求而言更为充裕，高于最佳或理论上的配置水平。而2017年则有9个省份为人力资本配置过度、21个省份人力资本配置不足，这一特征蕴含着该年人力资本供给水平低于经济发展的实际需求。综合而言，2000—2017年，中国人力资本的配置状况逐步由过度转向为不足。可能的原因是，2001年中国加入世界贸易组织以后，经济或产业全面融入全球化进程，外商直接投资的高速增长和中国城镇化、工业化的全面提速相互促进，中国经济规模的快速提升吸纳了相对配置过度的人力资本。再加之随着中国老龄化社会的到来，青壮年劳动力人口增长率下滑并于2012—2013年达到拐点开始走向负增长，使得人力资本供给相对于经济发展对人力资本的需求而言变得相对稀缺，从而中国整体上由人力资本配置过度转向配置不足。

为进一步考察中国八大经济区人力资本错配的时空演进特征及其可能存在的异质性，本文测算了2000—2017年八大经济区的人力资本错配指数。

限于篇幅，人力资本错配指数和人力资本错配指数核密度图未在正文列出，留存备索。2000—2017年，东北人力资本错配指数由2000年配置不足（大于0）演变为2014年的配置过度，且2014—2017年配置过度有加剧态势。原因可能在于，东北传统产业特别是制造业受国际贸易环境恶化和产业结构调整的冲击，相对于既有人力资本而言出现制造业投资萎缩，人力资本错配由不足向过度转变。北部沿海人力资本错配指数在0轴上方波动，始终表现为配置不足，且经历了两个加剧区间和两个缓解区间，呈现出大致M型的演变特征。北部沿海地区优质的开放环境和区位条件，吸引了大量外来资本流入，相对于更为旺盛的物质资本积累，人力资本相对配置不足。东部沿海人力资本错配指数在2012年前大于0，表现为配置不足，2012年后在0下方细微波动，表现为轻微的配置过度，但总体而言，该地区在样本期间人力资本错配得到有效缓解。东部沿海具有良好的就业创业环境，吸引了外来资本和人才的大量流入，相对于物质资本而言，人力资本稍显富足，但总体而言，人力资本配置状况得到明显改进，错配程度有所下降。南部沿海人力資本错配指数在波动中总体走高，并由2013年前的小于0转化为之后的大于0，说明该地区人力资本配置状况由配置过度向配置不足转变，且呈现出总体加剧态势。南部沿海地区开放的营商环境以及完善的产业设施，更容易获得资本的青睐，与此同时人力资本的积累速度相对不足，导致人力资本配置不足。黄河中游人力资本错配指数不断增大，数值由负转为正（2004年），说明人力资本配置状况由配置过度向不足演变，指数由2007年达到峰值后在波动中逐渐走低，说明配置不足的状况总体趋于缓解。黄河中游的人力资本呈现出逐年外迁的趋势，这也可能与周围沿海城市的虹吸效应息息相关。长江中游人力资本错配指数在0轴下方波动，其走势呈现出微弱的W型特征，说明该地区人力资本配置过度在经历了不断反复后趋于缓解。长江经济带建设带来的政策红利，加速的产业建设和投资，使得人力资本配置过度状况得到了有效的缓解。西南经济区人力资本错配指数在波动中不断增大，数值由负转为正（2015年），说明该地区人力资本配置过度在经历了较长时期的整体缓解后，开始呈现出配置不足特征，且有加剧趋势。西南经济区的人力资本底子薄，虽然积累速度较快，但与较发达地区还有很大的差距，随着西部大开发的纵深推进，相对于高速增长的投资规模而言，人力资本配置由过度向不足演进。西北经济区人力资本错配指数波动较为剧烈，但整体上也由配置不足向过度转化。西北经济区的资源禀赋相对匮乏，其人力资本积累也较为缓慢。

（四）基于核密度估计的中国人力资本错配结构性分析

依据人力资本错配核密度估计，2005年、2011年和2017年出现峰值波动，表明人力资本错配存在时间维度的结构性变化，因而将样本分为三阶段进行分析。与2000年相比，2005年核密度函数峰值明显升高，变化区间大幅度收窄，核密度函数中心向右移动穿过0值后更靠近0值，说明在2000—2005年，中国人力资本总体上表现为由投入过度向投入不足转变，人力资本错配得到矫正且各地区的差距明显缩小。与2005年相比，2011年峰值出现一定幅度回落，变化区间也出现扩大，密度函数中心略微向左靠近0值移动，说明在2005—2011年，中国人力资本错配得到略微矫正，但各地区的差距逐渐扩大。与2011年相比，2017年峰值较大幅度下降，变化区间也持续扩大，密度函数中心略微向左靠近0值移动，说明在2011—2017年，中国人力资本配置状况得到优化，但地区差距逐渐扩大。总体而言，与2000年相比，2017年人力资本错配的核密度函数中心向右移动穿过0值后更靠近0值，说明在2000—2017年，中国人力资本整体上表现为由投入过度向投入不足转变，波峰高度出现上升，变化区间逐渐缩小，这表明在中国30个省份人力资本错配程度降低，各省份人力资本错配差距变小。

四、人力资本错配指数的区域差异及来源

（一）基于三大地区分解的人力资本错配指数

根据式（5）—式（8）的计算方法，全国及东中西部三大地区人力资本错配指数差异的测度结果报告如表3所示。

从表3可以看出，人力资本错配指数的总体差异在波动中趋于上升，全国总体差异由2000年的0.289上升到了 2017年的0.336，上升幅度为16.3%。东部地区差异由2000年的0.199上升到了 2017年的0.498，上升幅度为150.3%，中部地区差异由2000年的0.466下降到了 2017年的0.278，下降幅度为40.3%，西部地区差异由2000年的0.265下降到了2017年的0.210，下降幅度为20.8%。从人力资本错配指数的区域对比来看，东部地区、中部地区和西部地区人力资本错配指数差异的均值分别为0.291、0.243和0.360，表明中部地区的人力资本错配指数差异最小，东部地区次之，西部地区最大。基于三大地区的分解结果显示，全国人力资本错配指数的差异主要来源于区域内差异，区域内差异贡献了总差异的93.9%，总差异中只有6.1%来自区域间差异。

（二）基于八大经济区分解的人力资本错配指数

为了进一步揭示人力资本错配指数的区域差异及来源，本文分别计算了东北、北部沿海、东部沿海、南部沿海、黄河中游、长江中游、西南和西北八大经济区的泰尔指数，并基于八大经济区对总体差异进行分解，结果如表4所示。从表4可以看出，北部沿海、东部沿海、南部沿海、黄河中游和西北的人力资本配指数差异在波动中趋于上升，而东北、长江中游和西南的人力资本错配指数差异在波动中趋于下降。从八大经济区人力资本错配指数差异的横向对比来看，东北的平均差异最小，北部沿海的平均差异最大，其人力资本错配指数均值分别为0.097和0.246。基于八大经济区的分解结果显示，人力资本错配指数总体差异主要由区域内差异和区域间差异共同引起，区域内差异贡献了总差异的 52.5%，区域间差异贡献了总差异的47.5%。

总体上看，基于三大地区，人力资本错配指数总体差异的主要来源是区域内差异，其中区域内差异贡献了总差异的93.9%;而基于八大经济区的分解结果显示，人力资本错配指数总体差异是区域内差异和区域间差异共同引起的，以上结果表明不仅要控制区域内差异，区域间的差异也同样值得重视。实际上，无论三大地区还是八大经济区的分解，都是从一个省份所处的地理位置来划分子群的，分解结果显示当地理区域划分较大时（三大地区），区域内差异对总差异的影响大，而区域间差异对总差异的影响小，而地理区域划分较小时（八大经济区），区域间差异对总差异的影响愈发明显，表明一个省份人力资本错配指数的高低有可能与地理位置存在某种关联性。

五、人力资本错配影响因素的经验考察

（一）变量界定与数据来源

1.被解释变量

人力资本错配指数（τLit），前文运用C-D生产函数，对2000—2017年中国30个省份的人力资本错配指数进行了测算，将其取绝对值后作为被解释变量。

2.解释变量

本文引入如下解释变量：（1）地方政府财政支出（lnlgs），以人均财政支出的自然对数表示。财政支出的直接投资效应及引致的社会资本政策引导效应，对区域物质资本形成及人力资本配置具有重要的影響，合理的财政支出规模及结构有助于要素配置效率的整体提升，反之，将对要素配置状况具有恶化效应。由此，财政支出将对人力资本配置具有重要影响。（2）教育水平（lnedu），以（小学人数×6+初中×9+高中×12+中职×12+大专×15+本科×16+研究生×19）/6岁以上人口计算所得的人均受教育年限的自然对数表示。受教育水平较低往往面临就业面狭窄的问题，而通常受教育水平越高，选择职业的自由度越大，人力资本在行业间的流动性更强，有利于缓解人力资本错配。（3）居民消费水平（lnhcl），以居民消费水平指数（2000年=100）计算的实际居民消费水平的自然对数表示。居民消费水平对劳动者的生产及生活环境具有重要作用，是引致物质资本投资和人才流动区位选择的重要变量，对人力资本配置具有重要影响。（4）信息化水平（it），以邮电业务总量与地区生产总值的比值表示。信息化发展有助于缓解物质资本和人力资本配置的信息不对称性，其引致的交易成本降低效应，有助于实现人力资本与其他要素资本的合理组合，进而对人力资本配置产生重要影响。（5）产业结构调整（ir），构建产业结构调整指数ir=∑3a=1Pa/Pln（Pi/Hi×H/P），其中，a为产业，i为省份，P为产出，H为就业人员数。这是一个反向指标，产业结构与就业结构耦合度最高时该指数为零，且全部为正，因而取倒数使之成为一个正向指标进入模型。产业结构调整对物质资本投资方向产生重要影响，并引致人力资本流动及配置方式的变革，通常产业结构变迁与人力资本配置调整不同步，产业的升级与发展落后或超前于人力资本配置水平的提高，均会加剧人力资本错配[8]。（6）贸易开放水平（trade），以进出口总额（万美元）×当年汇率与地区生产总值的比值表示。贸易开放水平是营商环境的重要组成部分，较高的贸易开放水平有助于物质资本和人力资本的形成及合理配置，从而缓解人力资本错配。（7）城镇化水平（urban），以城镇人口占总人口的比重表示。城镇化是产业及人口等要素资源向城镇地区逐步集聚的过程，城镇化建设引发的投资及人口流动效应，对各类要素配置具有重要影响，是引致人力资本配置调整的重要变量。

本文选取2000—2017年中国30个省份（不含西藏和港澳台地区）的数据作为样本，为消除数量级差异，本文对部分数据取自然对数。人均财政支出数据来源于中国财政税收数据库，其余解释变量的相关数据来源于历年《中国统计年鉴》。

（二）模型构建

区域经济一体化背景下的人力资本等生产要素的跨行政区域流动，使得人力资本配置效率可能在空间上具有相关性。上述区域泰尔指数的分解结果也显示出人力资本错配可能存在一定的地理空间关联，对于这种空间相关性的忽略必然导致在模型的估计上存在偏误以及进行错误的参数检验[25]ADDINNE.Ref.{13221427-2D66-4ABA-A263-E988F19D66DD}。空间计量模型由于考虑了变量存在空间转移扩散的情形，通过引入空间权重矩阵对可能存在的空间关联进行控制，有助于有效识别影响人力资本错配指数的时空因素。在空间计量模型的选择中，如果满足残差存在明显相关性或扰动项结构存在高阶空间依赖，则需要使用空间自相关模型（Spatial Auto Correlation Model，SAC），本文使用LM检验得出其残差存在显著相关性（在1%的水平上显著），因而构建计量模型如下：

τLit=ρωijτLit+δ1lnlgsit+δ2lneduit+δ3lnhclit+δ4itit+δ5irit

+δ6tradeit+δ7urbanit+εit（10）

其中，i和t分别表示省份和年份;ρ表示空间自回归系数;ωij作为二进制的邻接空间权重矩阵，表示不同地区之间的空间联系和互动关系，当省份i和省份j相邻时，ωij=1，当省份i和省份j不相邻时，ωij=0;εit表示随机扰动项。

（三）空间相关性检验

本文通过Moran's I及其散点图对中国人力资本错配指数进行全局空间自相关检验。Moran's I反映了观测值与空间滞后项的相关关系。Moran's I∈-1，1，其值大于零，表征高值与高值相邻、低值与低值相邻，说明具有正的空间相关性;其值小于零，表示高值与低值相邻，则说明具有负的空间相关性。如果其值接近零，则表明不存在空间自相关。

本文对中国30个省份人力资本错配指数的 Moran's I进行了空间自相关检验。检验结果显示：Moran's I 为0.1902，且通过了1%的显著性水平检验，这表明各省份人力资本错配指数在空间上存在依赖现象。进一步进行局部Moran's I检验，结果表明，人力资本错配指数在2000—2007年的空间相关性为负但不显著，2008—2017年的局部Moran's I均通过5%显著性检验，说明2008年以后，人力资本错配的空间相关性才逐渐显现。

（四）回归结果分析

表5是本文空间计量回归结果。

从表5可以看出，列（1）报告了式（10）各变量的点估计系数，其中，N=540，R2=0.100，ρ的估计值为-0.355，且在5%的水平下显著，误差项的空间自回归系数的估计值为0.372，且在1%的水平下显著，故存在空间自回归效应。同时LM检验和Robust LM检验均显著拒绝不存在空间相关性的原假设，这意味着本文采用空间自相关模型是合理的。列（2）—列（4）为采用偏微分方法对式（10）所报告的点估计系数进行的空间溢出效应分解，分别为直接效应、间接效应和总效应。

地方政府扩大财政支出规模加剧了本地区的人力资本错配，但对相邻地区的人力资本错配具有一定的缓解作用。总效应显著为正，说明地方政府财政支出总体上加剧了人力资本错配;提升消费水平有助于缓解本地区人力资本错配，但一定程度上加剧了相邻地区的人力资本错配，总体来看，消费水平的提升整体有助于缓解人力资本错配;信息化发展有助于缓解本地区人力资本错配，但在一定程度上加剧了相邻地区的人力资本错配，而总效应显著为负，说明信息化建设整体上有助于改善人力资本配置效率;第二、三产业的发展及其占比的上升，加剧了人力资本错配;加大教育投入以提升本地区劳动者的教育水平，提升贸易开放水平和加快城镇化进程对人力资本错配的影响均不显著。

（五）稳健性检验

空间计量模型的参数估计结果受到空间权重矩阵选取的影响较大，针对不同空间权重矩阵进行稳健性估计是有必要的。因此，本文分别采用经济距离空间权重矩阵、地理距离空间权重矩阵和经济距离与地理距离嵌套的空间权重矩阵进行稳健性检验。经济距离空间权重矩阵为ωeco，当省份i≠j，ωeco=1/gdpij，当省份i=j，ωeco=0，gdpij表示两个地区的经济距离，用人均GDP之差表示。地理距离空间权重矩阵为ωdis，当省份i≠j，ωdis=1/dij，当省份i=j，ωdis=0，dij表示两个省会城市的地理距离。经济距离与地理距离嵌套的空间权重矩阵如下：ω=σωeco+（1-σ）ωdis，0<σ<1，分别表示经济距离空间权重与地理距离空间權重各自所占比重。基于极大似然估计法对空间自相关模型进行估计，结果显示，绝大多数解释变量的符号方向和显著性与一致，这表明本文的估计结果是稳健的。限于篇幅，稳健性结果未在正文列出，留存备索。

空间计量模型的参数估计结果受到空间权重矩阵的选取的影响较大，针对不同空间权重矩阵下的估计进行稳健性估计是有必要的。因此，本文分别采用经济地理距离加权权重矩阵、经济距离权重矩阵以及地理距离权重矩阵进行稳健性检验。经济地理距离加权权重矩阵的空间权重矩阵如下：ω=σωeco+（1-σ）ωdis，0<σ<1，分别表示经济距离空间权重与地理距离空间权重各自所占比重;本文将取值为1，则定义的经济距离权重矩阵为：当省份i≠j，ωeco=1/gdpij，当省份i=j，ωeco=0，gdpij表示两个地区的经济距离，用人均GDP之差表示。ωdis为地理距离权重矩阵，当省份i≠j，ωdis=1/dij，当省份i=j，ωdis=0，dij表示两个省会城市的地理距离。基于极大似然估计法对空间自相关模型进行估计，结果显示，绝大多数解释变量的符号方向和显著性与前文保持一致，这表明本文的估计结果是稳健的。

限于篇幅，稳健性结果未在正文列出，留存备索。

六、主要结论与政策建议

在“粗放型”增长向高质量发展转型的背景下，人力资本要素在经济高质量发展过程中的作用更为凸显，矫正人力资本错配以提升人力资本的配置效率，有助于挖掘全要素生产率增长的潜力，实现经济的高质量发展。

本文利用C-D生产函数对2000—2017年中国30个省份的人力资本错配指数进行测度，从省级层面、区域层面考察了人力资本错配的类型和演进特征，通过泰尔指数对东中西三大地区和八大经济区人力资本错配的区域差异及来源进行揭示，通过空间计量模型检验了人力资本错配的空间关联及影响因素。研究结果表明：首先，2000—2017年中国各省份均存在明显的人力资本错配，错配类型由2000年的配置过度演变为2017年的配置不足，核密度估计结果显示，中国人力资本错配总体上得到缓解。八大经济区人力资本错配及其演化特征存在异质性：东北、东部沿海和西北经济区人力资本由配置不足向配置过度转化，且呈现出不断恶化趋势;北部沿海经济区存在人力资本配置不足问题;南部沿海、黄河中游和西南经济区存在人力资本配置过度转为不足且进一步加剧;长江中游经济区表现为人力资本配置过度。其次，人力资本错配指数区域差异较大，且差异呈现扩大趋势。基于三大地区和八大经济区的泰尔指数分解结果显示，全国人力资本错配系数的差异均主要来源于区域内差异。但与三大地区的分解结果相比，八大经济区人力资本错配指数的区域间差异的贡献率明显上升。最后，人力资本错配指数具有空间相关性，地方政府财政支出和产业结构调整对人力资本错配指数的改善有不同程度的阻碍作用;居民消费水平和信息化水平对人力资本错配都有不同程度的缓解作用，城镇化水平和贸易开放水平则对人力资本错配指数的影响不显著。

基于上述结论，笔者提出如下政策建议：

首先，提升人力配置不足地区的人力资本供给水平，消化过剩产能，促进人力资本供给的均衡化。总体上中国人力资本错配主要由配置过度向配置不足转变，这说明相对于经济发展对人力资本要素的最优需求而言，中国人力资本供给明显不足，应进一步落实好二胎、三胎政策以应对老龄化带来的青壮年劳动力数量下降的趋势。同时还应大力实施人才强国战略，加大社会保障、医疗保障、教育和培训的投入力度，提高人力资本的质量，以最大限度挖掘人力资本水平的提升潜力。

其次，差异化推进各省份或地区的人力资本错配矫正方案，促进人力资本的跨地区流动。

各省份人力资本错配程度及类型具有异质性，对于配置过度的东北、东部沿海、长江中游和西北经济区，应加大力度吸引外来产业或企业流入，以及通过政策引导与市场化机制相结合，引导过剩劳动力向人力资本配置不足的地区流动;而对于配置不足的北部沿海、南部沿海、黄河中游和西南经济区，则应通过跨区域合作，引导更多的产能向人力资本配置过度的地区转移，并通过积极的人才引进政策，引导劳动力流入人力资本配置过度的地区。上述战略或政策的有效实施，均需要各省份或地区的战略协同和政策合作。

再次，大力实施扩大内需战略，提升居民消费水平。考虑到居民消费水平的提升有助于缓解人力资本错配，各地区应大力实施扩大内需战略，以促进居民消费的数量和质量提升。例如，通过供给侧结构性改革，围绕居民消费的热点及升级趋势，优化企业产品或服务的供给方向，提升产品或服务的技术含量、品牌价值及附加值，以实现产品或服务供给与消费需求的有效匹配。

最后，大力发展以移动互联网和人工智能等数字技术为支撑的数字经济。信息化发展有助于从整体上缓解人力资本错配，应大力发展数字经济和提升地区信息化水平，通过数字经济与传统制造业和农业等的深度融合，促进产业的高质量发展。信息化和数字经济的发展也在一定程度上消减地区、省级之间的要素流动的交易成本，有助于人力资本在不同地区或不同省份之间的跨区域优化配置。

参考文献：

[1] Schultz， T.W.The Economic Value of Education[M].New York：Columbia University Press，1963.1-17.

[2] 蔡昉.中国改革成功经验的逻辑[J].中国社会科学，2018，（1）：29-44.

[3] 张佩.中国工业部门的行业间资源错配研究[J].投资研究，2013，（6）：15-27.

[4] 龚关，胡关亮.中国制造业资源配置效率与全要素生产率[J].经济研究，2013，（4）：4-15+29.

[5] 季书涵， 朱英明.产业集聚的资源错配效应研究[J].数量经济技术经济研究，2017，（4）：57-73.

[6] 白俊红，刘宇英.对外直接投资能否改善中国的资源错配[J].中国工业经济，2018，（1）：60-78.

[7] 李静， 楠玉， 刘霞辉.中国经济稳增长难题：人力资本错配及其解决途径[J].经济研究，2017，（3）：18-31.

[8] 解晋.中国分省人力资本错配研究[J].中国人口科学，2019，（6）：84-96.

[9] 胡鞍钢.从人口大国到人力资本大国：1980～2000年[J].中国人口科学，2002，（5）：3-12.

[10] 李海峥， 梁赟玲， Barbara Fraumeni，等.中国人力资本测度与指数构建[J].经济研究，2010，（8）：42-54.

[11] 龔关， 胡关亮.中国制造业资源配置效率与全要素生产率[J].经济研究，2013，（4）：4-15.

[12] 马颖， 何清， 李静.行业间人力资本错配及其对产出的影响[J].中国工业经济，2018，（11）：5-23.

[13] 葛晶， 李勇.行政垄断视角下人力资本错配的成因及其解释[J].中南财经政法大学学报，2019，（5）：43-52.

[14] 王宋涛， 温思美， 朱腾腾.市场分割、资源错配与劳动收入份额[J].经济评论，2016，（1）：13-25.

[15] 刘贯春， 张晓云， 邓光耀.要素重置、经济增长与区域非平衡发展[J].数量经济技术经济研究，2017，（7）：35-56.

[16] 杨志才.要素配置、收入差距与经济增长的实证研究[J].经济与管理研究，2019，（10）：16-29.

[17] 王启超， 王兵， 彭睿.人才配置与全要素生产率——兼论中国实体经济高质量增长[J].财经研究，2020， （1）：64-78.

[18] 李静， 楠玉.人力资本错配下的决策：优先创新驱动还是优先产业升级？[J].经济研究，2019，（8）：152-166.

[19] 李静.人力资本错配：产业比较优势演进受阻及其解释[J].统计与信息论坛，2017，（10）：95-101.

[20] Aoki， S.A Simple Accounting Framework for the Effect of Resource Misallocation on Aggregate Productivity[J].Japanese and International Economies，2012，26（4）：473-494.

[21] 陈永伟， 胡伟民.价格扭曲、要素错配和效率损失：理论和应用[J].经济学（季刊），2011，（4）：1401-1422.

[22] 赵志耘， 刘晓路， 吕冰洋.中国要素产出弹性估计[J].经济理论与经济管理，2006，（6）：5-11.

[23] 赵伟， 马瑞永.中国区域金融增长的差异——基于泰尔指数的测度[J].经济地理，2006，（1）：11-15.

[24] 张军， 吴桂英， 张吉鹏.中国省际物质资本存量估算：1952—2000[J].经济研究，2004，（10）：35-44.

[25] 王家庭， 贾晨蕊.中国区域创新能力及影响因素的空间计量分析[J].中国科技论坛，2009，（12）：73-78.

收稿日期：2021-07-02

基金项目：国家社会科学基金重大项目“全球生产核算的理论、方法和中国实践研究”（20&ZD134）;国家社会科学基金重点项目“2017年轮全球ICP方法和数据问题研究”（20ATJ001）

作者简介：杨仲山（1971-），男，陕西汉中人，教授，博士，博士生导师，主要从事国民经济核算和宏观经济统计分析研究。E-mail：yangzs@dufe.edu.cn

谢 黎（通讯作者）（1996-），男，重庆人，博士研究生，主要从事国民经济核算和宏观经济统计分析等研究。E-mail：dufexieli@163.com