基于TDLAS直接吸收法的气体压力测量技术研究
2021-12-17张博涵杨军魏伟谢兴娟张大治姜延欢
张博涵,杨军,魏伟,谢兴娟,张大治,姜延欢
(1.航空工业北京长城计量测试技术研究所,北京100095;2.空军装备部驻北京地区第四军事代表室,北京100043)
0 引言
气体压力是计量测试领域中最重要的测量参数之一,通常由传统的压力传感器进行定点测量,但受环境和空间的影响很大[1]。本文考虑利用可调谐半导体激光吸收光谱(Tunable diode laser absorption spectroscopy,TDLAS)[2]技术进行气体压力检测,此方法能够以控制温度和电流的方式来改变激光器输出的波长,调谐后的激光经过待测气室,可以扫描出一条完整的气体吸收谱线,进而从吸收谱线中获得气体的温度、压力、浓度等信息[3]。目前基于TDLAS技术进行气体检测的相关研究中,多是对痕量气体的检测工作,其中,齐汝宾[3]、李宁[4]、周茉[5]、禹迎春[6]等人进行了TDLAS技术气体浓度测量方面的研究;而此技术在气体压力测量方面的应用较少,陈祥[7]等人进行了TDLAS技术气体负压测量方面的研究,但现在还没有对气体中压测量方面的研究成果,所以若能够探究出吸收光谱技术在气体中压测量中的问题以及实现方法,对未来的光谱测量领域是很有意义的。
为了实现气体中压的光谱测量,文章从吸收光谱原理出发,以CO2作为研究对象,建立了基于积分吸光度的压力测量模型,利用MATLAB软件的Simulink可视化仿真模块对CO2在近红外波段处的吸收谱线进行仿真,并搭建了实验系统,进行常温环境下的气体中压测量实验,最后将仿真结果与美国光谱数据模拟工具SpectraPlot[8]的结果进行对比和分析;同时依靠仿真流程将实验测量得到的气体吸收谱线结果进行压力反演,得到气体压力结果,并进行了误差分析。
1 TDLAS直接吸收法测量原理
TDLAS直接吸收法利用一个低频段的锯齿波或者三角波调制激光输出波长,测量得到气体吸收后的光强信号,依据相关公式计算出气体压强,具体测量原理如图1所示。

图1 TDLAS直接吸收法原理Fig.1 Principle of TDLAS direct absorption method
1.1 朗伯-比尔定律
利用TDLAS技术来实现对气体压力的测量,其理论基础为朗伯-比尔(Beer-Lambert)定律[9],公式可表达为[1]
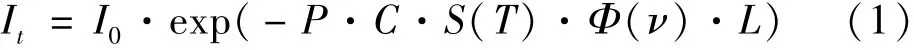
式中:It为透射光强信号,V;I0为入射光强信号,V;P为气体压强,atm;C为体积浓度;S(T)为谱线强度,cm-2·atm-1;Φ(ν)为吸收线型函数,表示待测气体吸收谱线的形状;ν0为激光频率,cm-1;L为光程,cm。
1.2 吸收谱线强度
谱线强度S(T)是关于气体温度T的函数[10],公式为
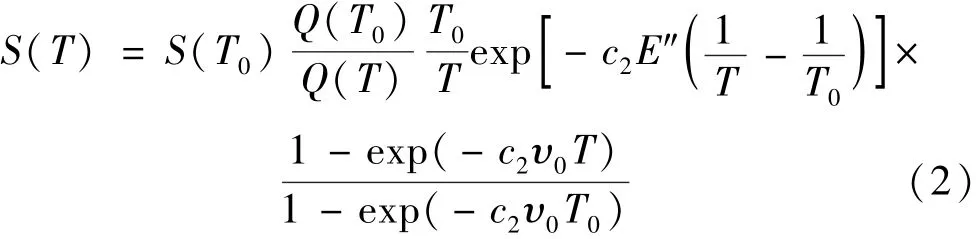
式中:S(T0)为参考温度T0下的谱线强度,cm-1/(molec·cm-2),一般可将HITRAN光谱数据库中在T0=296 K下的谱线强度数值作为参考;Q(T)为吸收分子的配分函数;c2=hc/k(h为普朗克常数,c为光速,k为波尔兹曼常数);E″为吸收气体分子跃迁时对应的低能级能量,cm-1;v0为吸收谱线的中心频率。
式中:配分函数Q(T)常采用拟合的三次多项式来替代,公式为

式中:系数a,b,c,d因不同的气体和温度取不同的值。
1.3 吸收线型
通常用来表达气体吸收谱线的线型函数有三种:多普勒(Doppler)线型函数、洛伦兹(Lorentz)线型函数和沃伊特(Voigt)线型函数。其中在压力较大,温度因素对气体吸收光谱影响较小时多采用洛伦兹线型函数[3]。本次仿真通过利用洛伦兹线型函数来表达气体吸收过程中的谱线线型。
其函数表达式为[4-6]
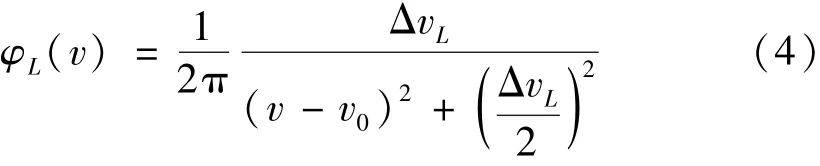
式中:v为激光扫描波长范围;v0为对应谱线的跃迁频率;ΔvL为吸收谱的半高宽[4],cm-1。

式中:A为待测气体;P为总压强;XB为碰撞干扰气体B的摩尔份数;γA-B为碰撞加宽系数,cm-1·atm-1,大小与温度有关[4],其关系式为
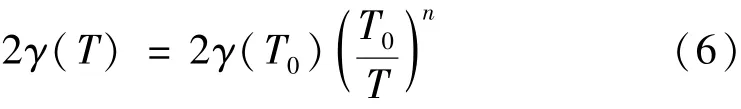
式中:T0为参考温度;γ(T0)为加宽系数;n为温度指数,可从HITRAN数据库获得[4]。
2 系统仿真和实验
2.1 系统仿真模型
利用Simulink仿真工具,对TDLAS压力测量系统的各个模块进行仿真,包括光源模块、吸收池模块,数据采集模块[12]。总体仿真流程和系统仿真结构如图2和图3所示。
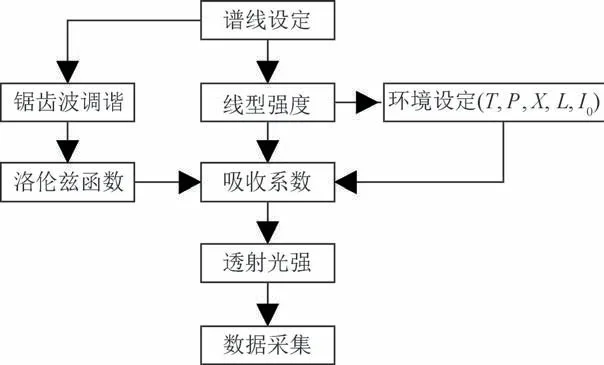
图2 仿真流程图Fig.2 Simulation flow chart
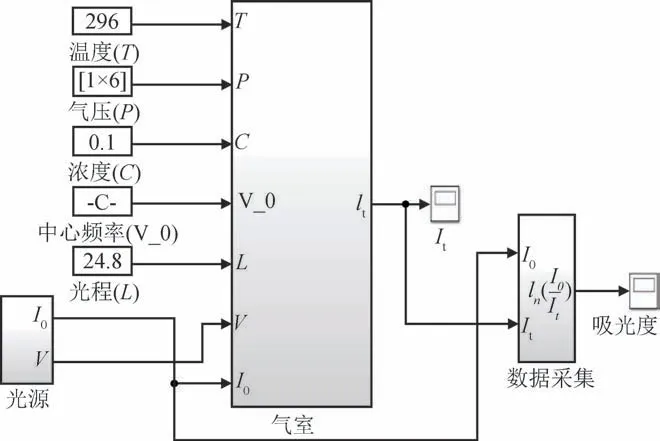
图3 TDLAS气体压力测量系统仿真结构图Fig.3 Simulation structure diagram of gas pressure measurement system based on TDLAS
2.1.1 光源模块
光源仿真模块包含谱线设定和锯齿波调谐,如图4所示。利用50 Hz的低频锯齿波作为调谐信号,调谐后的激光强度和激光频率的数学模型可表达为
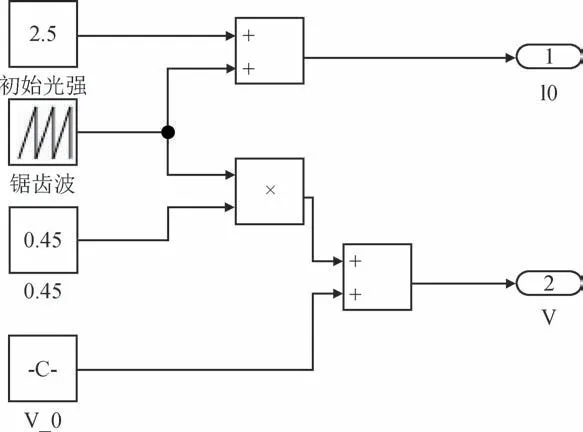
图4 光源仿真模块Fig.4 Light source simulation module

式中:νt为激光器的输出频率,cm-1;ν0为中心频率,cm-1;It为输出光强,V;I0为基础光强,V;Am为锯齿波的幅度;aν,bI分别为频率和光强随调谐信号变化的系数。
设置基础光强信号为2.5 V,锯齿波幅值设置为-1~1 V,周期为20 ms,系数bI设置为1,ν0设置为4989.9714 cm-1,系数aν设置为0.45。
2.1.2 气室模块
气室模块包含洛伦兹函数仿真、线型强度仿真和环境设定。主要依据CO2气体在4989.9714 cm-1处的洛伦兹吸收谱线线型函数进行设计,模拟密闭气室中的气体吸收的过程。根据式(3)~式(5)建立谱线强度函数S(T),CO2配分函数Q(T)和线型函数Φ(ν)仿真模型,如图5所示。根据HITRAN光谱数据库选择CO2吸收谱线的相关参数,并根据实验室条件设定吸收气体环境参数,如表1所示。

表1 参数设定Table.1 Parameter setting
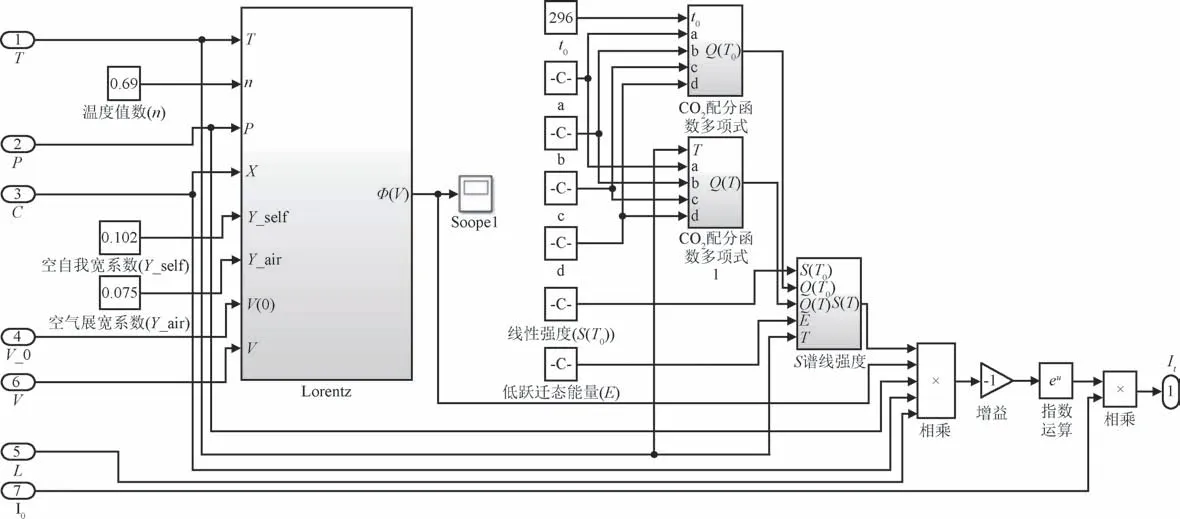
图5 气室模块Fig.5 Air chamber module
2.1.3 数据处理模块
数据处理单元包含透射光强信号采集和气体吸光度计算两部分,如图6所示。其吸光度表达式为[1]

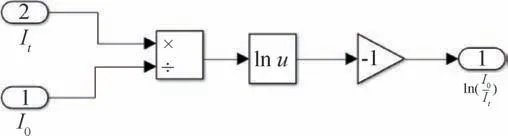
图6 数据采集模块Fig.6 Data acquisition module
2.2 实验系统
根据仿真模型,搭建了如图7所示的实验系统进行实验测量,将测量得到的吸收谱线信号It进行处理,并进行压力反演。根据式(1)和式(8),可得压力计算表达式


图7 TDLAS直接吸收法压力测量实验系统Fig.7 Pressure measurement experimental system based on TDLAS direct absorption method
3 结果
3.1 仿真结果
1)线型曲线和吸收谱线
根据上述压力测量仿真模型,得到压力变化引起的洛伦兹线型函数曲线仿真结果如图8所示,当激光经过气室,得到CO2吸收光谱仿真结果如图9所示。可以看出随着压力的增加,洛伦兹线型函数峰值不断减小,吸收谱线的信号强度减小。

图8 洛伦兹线型函数仿真图Fig.8 Lorentz linear function simulation diagram

图9 吸收谱线仿真图Fig.9 Simulation diagram of absorption spectrum
2)吸光度曲线
由数据采集模块输出的数据为气体吸光度值,将仿真得到的吸光度曲线和SpectraPlot的吸光度曲线进行对比,如图10所示,可以看出仿真结果与Spectra-Plot结果有很好的重合度,证明了此仿真模型的可行性。此外,随着压力的增加,谱线展宽越来越大,而且在ν=ν0时,吸光度值达到峰值,即0.3左右,气体吸收现象比较明显。

图10 296 K温度下仿真结果与SpectraPlot结果Fig.10 Different pressure simulation results and SpectraPlot results at 296 K
3)积分吸光度
将上述的吸光度-频率曲线进行积分,得到的曲线积分面积即为积分吸光度[13]。计算得到各压力下的积分吸光度值,结果如表2所示。然后将积分吸光度与压力进行曲线拟合,拟合结果如图11、图12和表3所示。
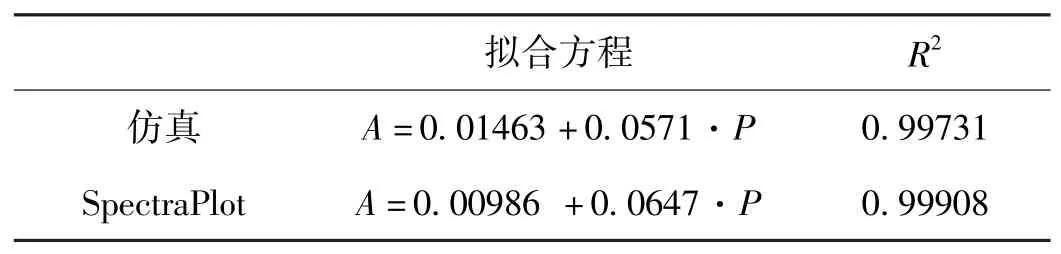
表3 积分吸光度-压力拟合结果Table.3 Integral absorbance-pressure fitting result
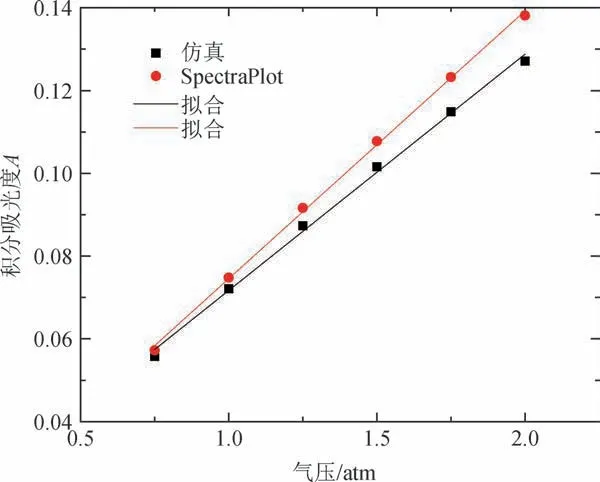
图11 积分吸光度对比图Fig.11 Integral absorbance comparison chart

图12 积分吸光度仿真结果相对误差Fig.12 Relative error of integral absorbance simulation results

表2 积分吸光度计算结果Table.2 Integral absorbance calculation result
由以上数据可知,随着压力的增大,积分吸光度值也以正比例关系增加,同时仿真结果与SpectraPlot结果的误差也在变大,最小相对误差为2.6%,最大相对误差不到8%,拟合曲线的斜率相差0.0076。
仿真结果相对偏差随压力增大而增加的主要原因为:在压力较大的情况下,仿真选择的洛伦兹线型函数限制了气体吸收谱线的峰值吸光度,减弱了相邻谱线的相互影响,致使积分吸光度计算误差变大。
3.2 实验结果
利用图7中的实验系统,进行常温条件下的压力测量实验,测得气体吸收后的光强信号如图13所示。
利用多项式拟合的方式从测量得到的吸收谱线信号中拟合背景基线,根据式(8)可以得到吸光度曲线,结果如图14所示。由图可知:随着压力增大,谱线展宽也随之变大,这与仿真结果一致;吸光度曲线两侧波动比较大,这会导致数据函数拟合结果产生较大误差,所以选择曲线中间的数据点进行拟合,拟合结果如图15所示。
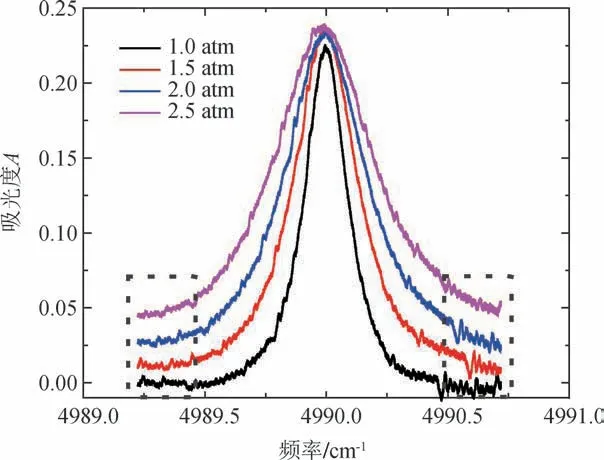
图14 吸光度曲线Fig.14 Absorbance curve
对图15拟合得到的线型函数进行频率积分,得到各个压力下的积分吸光度值,根据式(9)和仿真过程中的参量(表1),计算得到压力值,如表4所示。

图15 不同压力吸光度曲线Lorentz函数拟合Fig.15 Lorentz function fitting results of absorbance curves at different pressures

表4 压力测量结果
由表4可以看出,常温环境下,随着压力的增大,测量结果相对偏差也在增加,主要是因为:当压力增大时,相邻吸收谱线的影响程度加大,吸光度曲线被横向拉宽变得平缓,偏离零基线,导致其洛伦兹函数拟合误差变大,从而使计算得到的压力结果随之增大。
4 结论
本文对基于TDLAS直接吸收法的CO2气体压力测量原理进行了阐述,利用Simulink工具进行了理论仿真,提供了相应的参数选择,并搭建实验系统进行了实验。结果表明:在中压阶段,随着压力的增加,气体吸收谱线间的相互影响程度加深,测量相对误差增加。研究过程对推动吸收光谱技术在气压测量领域的应用具有重要意义。而如何解决在压力较大的气体环境下,吸光度曲线偏离零基线的问题和提高光谱技术测量精度的问题将是未来的研究重点。
