液体火箭发动机试验流量测量系统可靠性评定

杨懿,郭亚男,王永鹏,贾志杰,陈文丽,吕守国,吉喆

(北京航天试验技术研究所,北京100074)

0 引言

液体火箭发动机试验中,液体推进剂的流量数据是计算发动机比冲量的重要数据,测量数据的准确性和可靠性关系到对火箭的运载能力和射程的评估[1]。流量测量系统的高可靠性是保障系统长期正常、稳定工作,测量数据满足试验任务书要求的重要基础。

在可靠性研究和实践领域,一般从结构可靠性和性能可靠性两个维度对产品/系统的可靠性进行评估。性能可靠性一般是指产品/系统在规定工作条件下、规定工作时间内,其性能参数满足规定的容许限要求的概率[2-3]。如导弹的射程、着弹点的准确度,测量系统的数据准确度等等。结构可靠性一般是指产品/系统保持正常工作、性能满足规定要求的能力[4]。在发动机试验中,测量系统的性能可靠性与结构可靠性是同等重要的。性能可靠性是测量系统能够投入使用的前提和保障测量数据质量的重要基础。结构可靠性是保障测量系统能够长久、正常运行的重要基础。在测量系统的工作寿命周期内,不仅需要具备优越的性能可靠性,还需要具备保持其性能可靠性的能力。多位研究人员对产品的性能可靠性、功能可靠性评估方法进行了研究。

陈保家等人[5]从轴承运行数据中提取状态信息和设备的阈值信息,采用基于比例协变量和Logistic回归模型相结合的可靠性评估方法求解故障率和协变量函数,并不断更新故障率函数信息,从而提高航空发动机轴承运行可靠性评估精度和可信性。但是由于航天产品试验的测量系统一般由多个组成单元或者设备构成,彼此之间的测量原理、测量参数类型存在差异,确认测量系统的阈值信息存在较大的困难,该方法不适用于对测量系统可靠性的评估。

张曌等人[6]采用故障树方法分析多个影响测量系统可靠性的因素,给出了影响因素的重要度排序,并对测量系统进行故障诊断,有效提高了系统的平均无故障时间和连续工作时间。但是该方法重点在于实现测量系统的定性分析,缺少对测量系统性能可靠性的分析,也未给出系统可靠性的定量评价方法。

叶亮等人[7]根据轴承的数据特征,采用不同的指标描述轴承振动性能,建立不同指标和振动性能可靠性之间的关系。采用基于信息理论和概率统计的方法计算、分析轴承振动性能的可靠度。其研究的重点是基于数据特征来描述性能可靠性,对本文有一定启发。该方法并未考虑结构功能可靠性对产品可靠性的影响,而且当发动机在多工况下试验时,流量的变化必然导致数据表征指标相应变化,增加了评估的难度,并不适用本文的研究方向。

张根保等人[8]将机电产品分解成最小的元动作单元,将产品性能可靠性问题转化为元动作单元性能可靠性问题。根据元动作单元内部零件和结构的依赖耦合关系,建立随机过程和元动作单元性能可靠性分析模型,分析产品性能退化与特定功能之间的关系。该方法适用于对机械产品的结构可靠性评估,缺少对性能数据的分析。而测量系统性能可靠性指标主要以大量实测数据为基础,对实测数据的合理分析是判断性能可靠性的主要依据。

综上所述,单从结构可靠性或者性能可靠性对液体火箭发动机试验流量测量系统的可靠性进行分析是远远不够的。需要将性能可靠性和结构可靠性结合起来,实现航天产品试验测量系统可靠性的定量分析。本文给出了行业背景下测量系统性能可靠性和结构可靠性的定义,将试验数据作为性能可靠性的衡量指标,将测量系统组成单元的失效数作为结构可靠性的衡量指标。从性能可靠性和结构可靠性两个维度对液体火箭发动机流量测量系统的可靠性进行评估。对行业内技术人员评估测量系统指标具有重要的参考价值。

1 流量测量系统

在液体火箭发动机试验中,流量测量系统一般由涡轮流量计、信号发生器、二次仪表和数据采集系统组成[9]。系统原理组成如图1所示。

图1 流量测量系统图Fig.1 Diagram of flow measurement system

流量参数的基本测量原理:推进剂经过贮箱增压后,推动涡轮流量计的叶轮转动。转动叶轮切割信号发生器所产生的磁力线,生成正弦波式感生电动势。当管路横截面积不变时,感生电动势的频率与推进剂流速成正比。频率和被测流量的线性关系为

式中:Q为通过传感器的体积流量,L/s;A,B为传感器常数;f为传感器输出频率,Hz。

2 流量测量系统可靠性定义及评定方法

2.1 测量系统性能可靠性定义

根据引言中性能可靠性的定义,针对测量系统的特殊性,需要对其性能可靠性的定义进行相应的扩充,其定义如下。

测量系统性能可靠性是指在规定的时间内和规定的条件下,测量系统工作正常,系统输出的测量数据满足所规定的允许限度要求的能力或概率。其中,规定时间是指系统完成试验测量任务所需的时间。规定条件是指系统工作时所处的符合对应要求的全部外界条件,如环境、温湿度、振动等。正常工作是指系统的各项组成单元均工作正常。

2.2 性能可靠性评定方法

大量的试验统计数据表明,液体火箭发动机性能参数(推力、比冲、流量、混合比等)一般服从正态分布[2]。因此,设系统的性能X~N(μ,σ2),其中,μ,σ未知。对X取容量为n的样本x1,x2,…,xn,通常要求系统的性能参数保持在容许的偏差范围之内,则

式中:X0为性能参数的额定值;ΔX为性能参数容许的偏差范围。

可以得到

式中:XU为性能参数的容许上限;XL为性能参数的容许下限。

在可靠性理论中,根据产品/系统的功能定位,对性能参数的要求大致可以分为3类[10]:

1)单侧下限参数性能可靠性

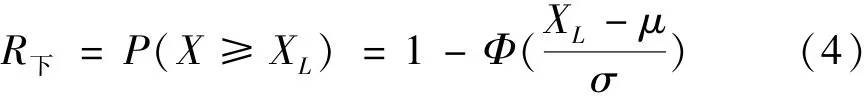
2)单侧上限参数性能可靠性

3)双侧参数性能可靠性,即XL≤X≤XU。

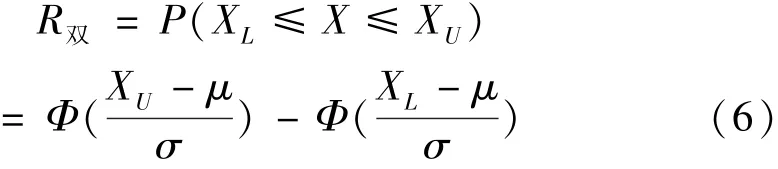
一般情况下,只能通过产品的有限次试验或者有限个系统试验测试数据得到性能X的样本均值与样本标准差S。以样本均值与样本标准差S分别替代μ,σ求得性能可靠性的点估计。区间估计的推导方法为[2]等价于令,

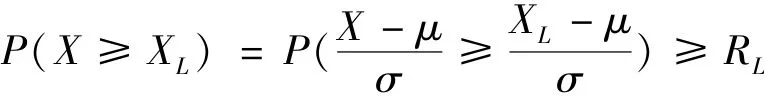
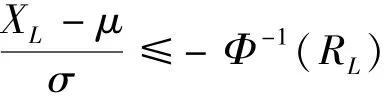
则有,

通过调整变换得到

等价于

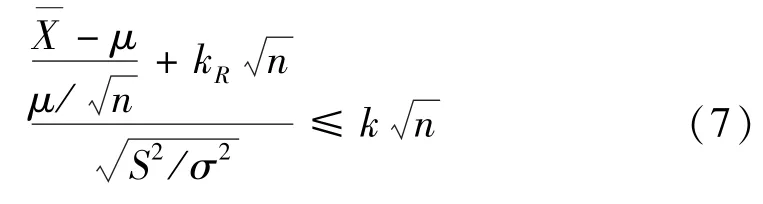
在置信水平γ下,计算γ,即

由上述分析可知,当给定置信度γ,已知参数k,n时,即可求出kR,从而求得性能可靠性单侧下限RL=Φ(kR)。由于求解计算的过程较为较为复杂,可以通过查表的方式进行求解。求解方法如下:

2)根据给定的置信水平γ,样本量n和k值,对于单侧置信下限可靠度,可以查参考文献[11],求解kR值,从而可得到置信下限可靠度RL=Φ(kR)。对于双侧置信下限估计,可以查参考文献[12]求得近似解。

2.3 测量系统结构可靠性定义

根据引言中结构可靠性的定义,针对测量系统的特殊性,其结构可靠性的扩充定义为:

测量系统结构可靠性是指测量系统各组成单元在规定的时间内和规定的条件下正常工作的概率。其中,规定时间是指测量系统在系统调试、正式试验等程序中的工作时间。规定条件主要是指测量系统需要满足试验任务书规定的相关要求。

2.4 结构可靠性评定方法

在液体火箭发动机试验以及系统调试等过程中,影响流量测量系统结构可靠性的因素主要有以下几个方面:

1)涡轮流量计的轴承、叶轮等部件长时间受气流、低温介质的高速推动,容易损坏。

2)受液氧、液氢等低温介质的影响,涡轮流量计外接信号发生器频繁处于温差变化较大的环境中,严重影响信号发生器的工作稳定性。接插件暴露在空气中,冷凝现象也影响了接插件的可靠性。

基于上述原因,对流量测量系统的结构可靠性进行研究和分析,对提高流量测量系统可靠性具有重要的意义。氢氧火箭发动机试验流量测量系统可靠性框图如图2所示。

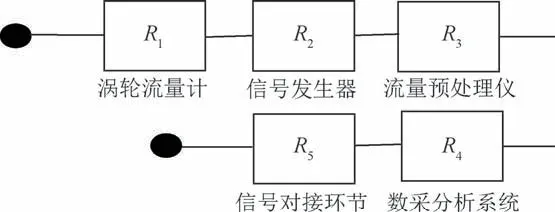
图2 流量测量系统可靠性框图Fig.2 Reliability block diagram of flow measurement system

图2 中,信号对接环节主要是指流量测量系统在运行过程中,设备接插件(如流量计信号发生器的插头、流量预处理仪的插头等)的对接状态。根据以往的统计数据显示,接插件的对接状态也是影响流量测量系统是否正常工作的重要因素之一。因此,本文将信号对接环节作为影响系统可靠性的因素,纳入可靠性框图中。

从图2可知,流量测量系统结构可靠性为一般串联系统。工程应用中一般采用L-M法对系统可靠性进行近似求解。根据串联型系统可靠性的性质,系统的可靠性由组成系统的最薄弱单元决定[2]。

图2 中,涡轮流量计、信号发生器、流量预处理仪(R1~R3)的单元失效类型为寿命型,数采分析系统(R4)和信号对接环节(R5)的失效类型为成败型。为便于可靠性试验信息的折合,需要将不同失效类型数据转换为相同失效类型数据。本文将指数寿命型试验信息转换为二项成败型试验信息。文献[13-14]介绍了指数型与成败型试验数据的折合转换方法,本文不再赘述。

L-M法的基本原理[10]为:设系统由k个单元组成,试验数据为(ni,Fi),其中,i=1,2,…,k,ni为第i个单元的试验次数,Fi为第i个单元的失败试验次数。则系统可靠性最大似然估计为

将系统各组成单元的试验次数按照从小到大的顺序排列,{n(1),n(1),…,n(k)}为将ni,(i=1,2,…,k)重新进行排列后的数据集,取系统等效试验次数为

系统等效失败次数为

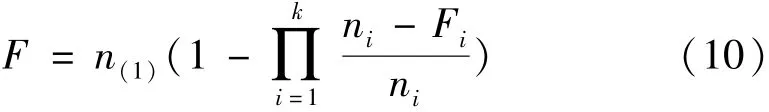
设[F]为不超过F的整数部分,在给定置信水平γ时,通过公式(11),(12)计算R1和R2。再采用线性插值法,得到失败次数为F时的系统可靠性置信下限RL。

3 案例分析

以某型号发动机试验为例,对流量测量系统可靠性进行评定。

3.1 测量系统性能可靠性评定

根据任务书的要求,在某工况下,液氧额定流量为5.200 L/s,下限为5.096 L/s,上限为5.304 L/s,给定置信水平γ=0.9。选取该工况下10个子样的液氧流量数据,如表1所示。

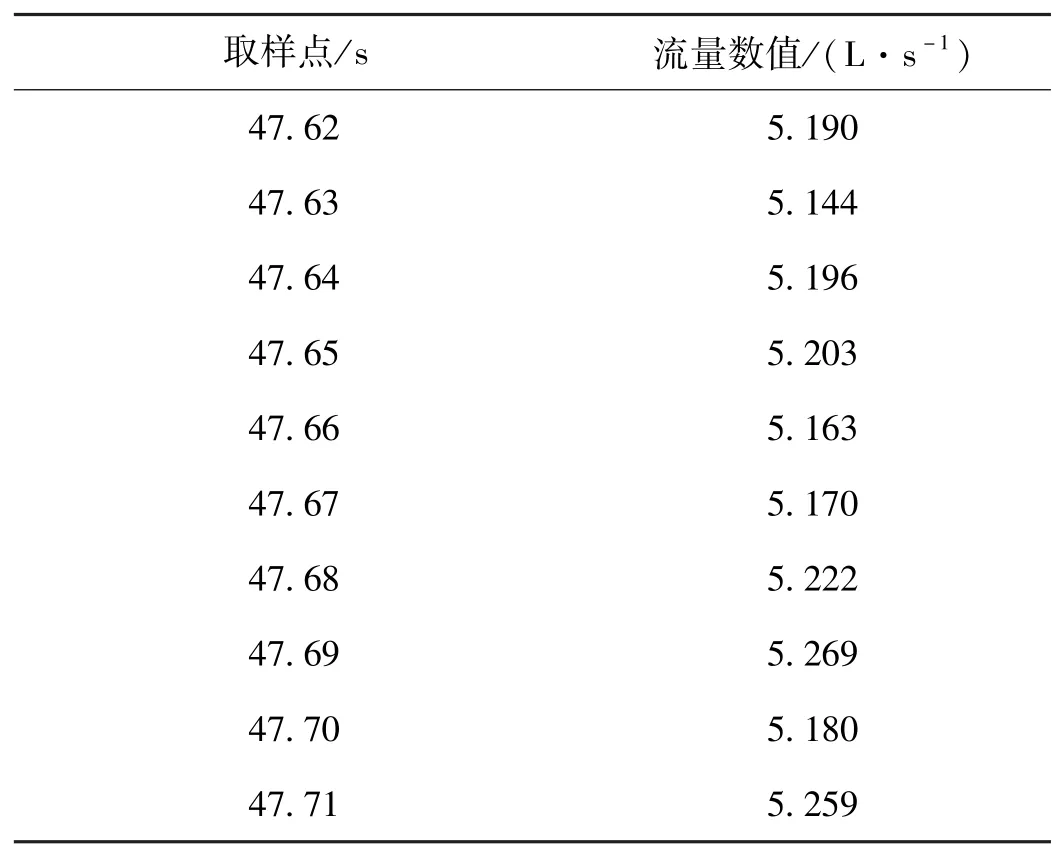
表1 液氧流量数据表Table.1 Data sheet of liquid oxygen flow

可靠度估值

根据n=10,γ=0.9,k1=2.5660,k2=2.5859,查《正态分布双侧容许限系数表》得到p1=0.00745,p2=0.00726。计算得到测量系统性能可靠性下限RL=1-(p1+p2)=0.98529。

3.2 测量系统结构可靠性评定

取置信水平γ=0.9,测量系统各组成单元的等效试验数据如表2所示。

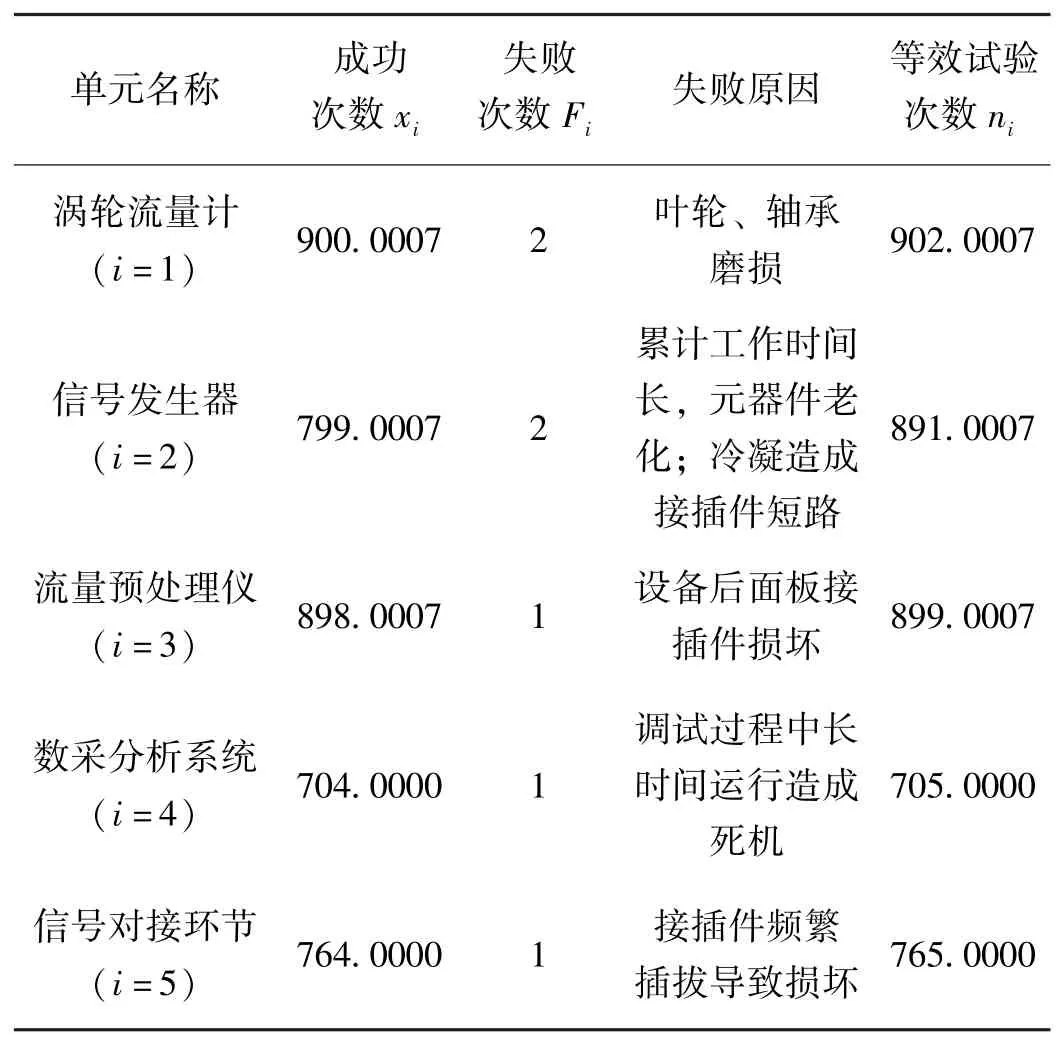
表2 流量测量系统各组成单元等效试验数据表Table.2 Equivalent test data of each unit of flow measurement system

根据表2的数据,将系统各组成单元的试验数按照从小到大的顺序排列{705.0000,765.0000,891.0007,899.0007,902.0007},取系统等效试验次数为n(1)=705.0000。则最大似然估计为

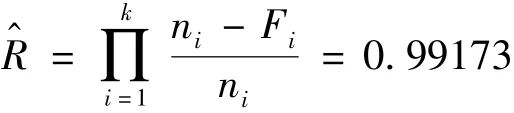
等效失败次数F为

根据公式(11)、(12)得到

求解上述方程得到R1=0.98511,R2=0.98688。根据(F=6,R1=0.98511)和(F=5,R2=0.98688),采用线性插值法求得当失效数F=5.83035时,置信下限RL=0.98521。

4 总结

测量系统的性能可靠性和结构可靠性是衡量测量系统的两个重要的指标。本文从性能可靠性和结构可靠性两个维度评定液体火箭发动机试验流量测量系统可靠性。

1)根据试验任务书给出的流量上下限值,以及试验数据的分布特征,采用双侧性能可靠性方法,计算得到性能可靠性置信下限,得到性能可靠性的下限值为0.98529。虽然高于试验任务书对发动机的可靠度要求(0.98000),但是还有较大的提升空间。

2)建立流量测量系统可靠性框图以及串联系统的特征,将流量测量系统组成单元中指数失效型数据转换为成败型失效数据,采用L-M法和线性插值法计算得到系统结构可靠性置信下限为0.98521。其结果虽然满足要求,但是还存在较大的优化余地。表2中的失败次数和失败的原因为提高测量系统结构可靠性指明了方向。提高产品质量、加强设备和零部件使用寿命的分析以及及时更换接插件等方法是有效提高结构可靠性的手段。

综上所述,虽然本文所采取的可靠性评估方法只得出了系统可靠性的近似解,但是针对测量系统的特殊性,上述评估方法对行业内测量技术人员合理评价测量系统可靠性、研究提高系统可靠性方法提供了重要的参考。