基于实验项目的中心极限定理教学设计

熊梅 张大林

摘 要 中心极限定理在概率论与数理统计中具有首席定理之称，是概率论与数理统计教学过程中的一个重难点。本文将实验项目融入中心极限定理的教学过程之中，设计了数值模拟和图形模拟两个实验项目，并利用MATLAB软件实现。对于数值模拟项目，将实验数值与理论数值进行比较，得到中心极限定理直观的近似结果。对图形模拟项目，展示了中心极限定理蕴含的极限变化过程，使得抽象的教学内容具体化、直观化和形象化，加深了学生对中心极限定理的理解，提高了课堂教学效果。

关键词 中心极限定理;实验项目;MATLAB;教学设计

中图分类号：G424                                 文献标识码：A  DOI：10.16400/j.cnki.kjdk.2021.33.032

Teaching Design of Central Limit Theorem Based on Experimental Project

XIONG Mei， ZHANG Dalin

（School of Mathematics and Statistics， Qiannan Normal University for Nationalities， Duyun， Guizhou 558000）

Abstract The central limit theorem is called the chief theorem in probability theory and mathematical statistics. It is significant and difficult in the teaching process of probability theory and mathematical statistics. In this paper， the experimental projects are integrated into the teaching process of the central limit theorem， and two experimental projects， numerical simulation and graphic simulation， are designed and realized by using MATLAB software. For the numerical simulation project， comparing with the theoretical value the intuitive results approximated of the central limit theorem is obtained. The graphic simulation project shows the limit changing process contained in the central limit theorem， which makes the abstract teaching content concretized， intuitional and visualized， deepens students' understanding of the central limit theorem and improves the classroom teaching effect.

Keywords central limit theorem; experimental project; MATLAB; teaching design

在自然界中，一些現象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。中心极限定理是概率论的重要内容，也是数理统计学的基石之一，是概率论与数理统计课程教学中的一个重难点。在实际教学过程中，由于中心极限定理本身的抽象性和结果的多样性使得学生容易产生畏难情绪，导致学生很难准确深入理解中心极限定理的实质。

1 中心极限定理的表述

中心极限定理的第一版是被法国数学家棣莫弗发现的，他在1733年发表的卓越论文中使用正态分布去估计大量抛掷硬币出现正面次数的分布。 这个超越时代的成果险些被历史遗忘，所幸著名法国数学家拉普拉斯在1812年发表的巨著《概率分析理论》中拯救了这个默默无名的理论。 拉普拉斯扩展了棣莫弗的理论，指出二项分布可用正态分布逼近。1901年，俄国数学家里雅普诺夫用更普通的随机变量定义中心极限定理，并在数学上进行了精确的证明。如今，中心极限定理被认为是（非正式地）概率论中的首席定理。主要表述为： Lindeberg-Levy中心极限定理（独立同分布中心极限定理）、De Moivre-Laplace中心极限定理（二项分布的正态近似）和Lyapunov中心极限定理（独立但不同分布中心极限定理）。[1]其中De Moivre-Laplace中心极限定理是独立同分布中心极限定理的特殊情况，而Lyapunov中心极限定理则比独立同分布中心极限定理更具有一般性。

1.1 De Moivre-Laplace中心极限定理

设随机变量服从参数为的二项分布，即则对于任何实数有下式成立：

1.2 Lindeberg- Levy中心极限定理

设随机变量相互独立且服从同一分布，数学期望和方差都存在且方差不为0，即，，，则对于任何实数有下式成立：

1.3 Lyapunov中心極限定理

设随机变量相互独立，且数学期望，方差，记。 若满足如下Lindeberg条件：存在，使得时，有

则

这个定理证明了由大量微小的而且独立的随机因素引起并累积而成的变量，必将是一个正态随机变量。

2 中心极限定理的实验项目设计

中心极限定理究竟说明的是一个什么样的现象，它反映了怎样的统计规律和分布特征呢？除了数学理论上的证明外，我们还可以通过实验的形式，来直观的理解和掌握中心极限定理的本质特征。下面两个实验项目的实现可以发现，当独立随机变量的个数不断变大时，随机变量之和的分布会趋向于正态分布。这一现象指出了正态分布使用范围之广的原因，也间接证明了正态分布在实际案例中起到了关键作用。[4]

2.1 数值近似实验项目

设随机变量服从参数为0.5的泊松分布，即～（0.5），其30次重复观测结果为，记

用计算机模拟的重复观测结果1000次，将的经验分布函数（）与在点

，

的值相比较，并解释比较结果。[2]

解：在Matlab命令窗口中输入代码：

>>y=poissrnd（0.5，1000，30）;得到一个1000？0阶的矩阵该矩阵的每一行可以看作的一次30次重复观测的模拟结果。

执行代码：>>xm= （mean （y，2）-0.5）*sqrt（60）;

得到1000维的列向量，它是每个分量都是的一次重复观测的模拟结果。

运行代码：>>sum（[xm<-3，xm<-2.5，xm<-2，xm<-1.5，xm<-1，xm<-0.5]）/1000

得到的经验分布函数在-3，-2.5，-2，-1.5，-1，-0.5处的值：

ans=  0.0000   0.0000   0.0220   0.0790   0.1900   0.3670

>>sum（[xm<0，xm<0.5，xm<1，xm<1.5，xm<2，xm<2.5，xm<3]）/1000

得到的经验分布函数在0，0.5，1，1.5，2，2.5，3处的值：

ans=  0.4740   0.6640   0.8110   0.9220   0.9680   0.9860   0.9960

>>normcdf（-3：0.5：3，0，1）

得到分布函数在点的值，0≤k≤12。

ans=  Columns 1  through 7

0.0013    0.0062    0.0228    0.0668    0.1587

0.3085   0.5000

Columns 8  through 13

0.6915    0.8413    0.9332    0.9772    0.9938

0.9987

将所得的经验分布函数和正态分布函数的值列入表1。比较两个分布函数在相同点的值，发现它们的最大误差不超过0.06，说明用标准正态分布函数来近似的经验分布函数的效果还是比较好的（表1）。

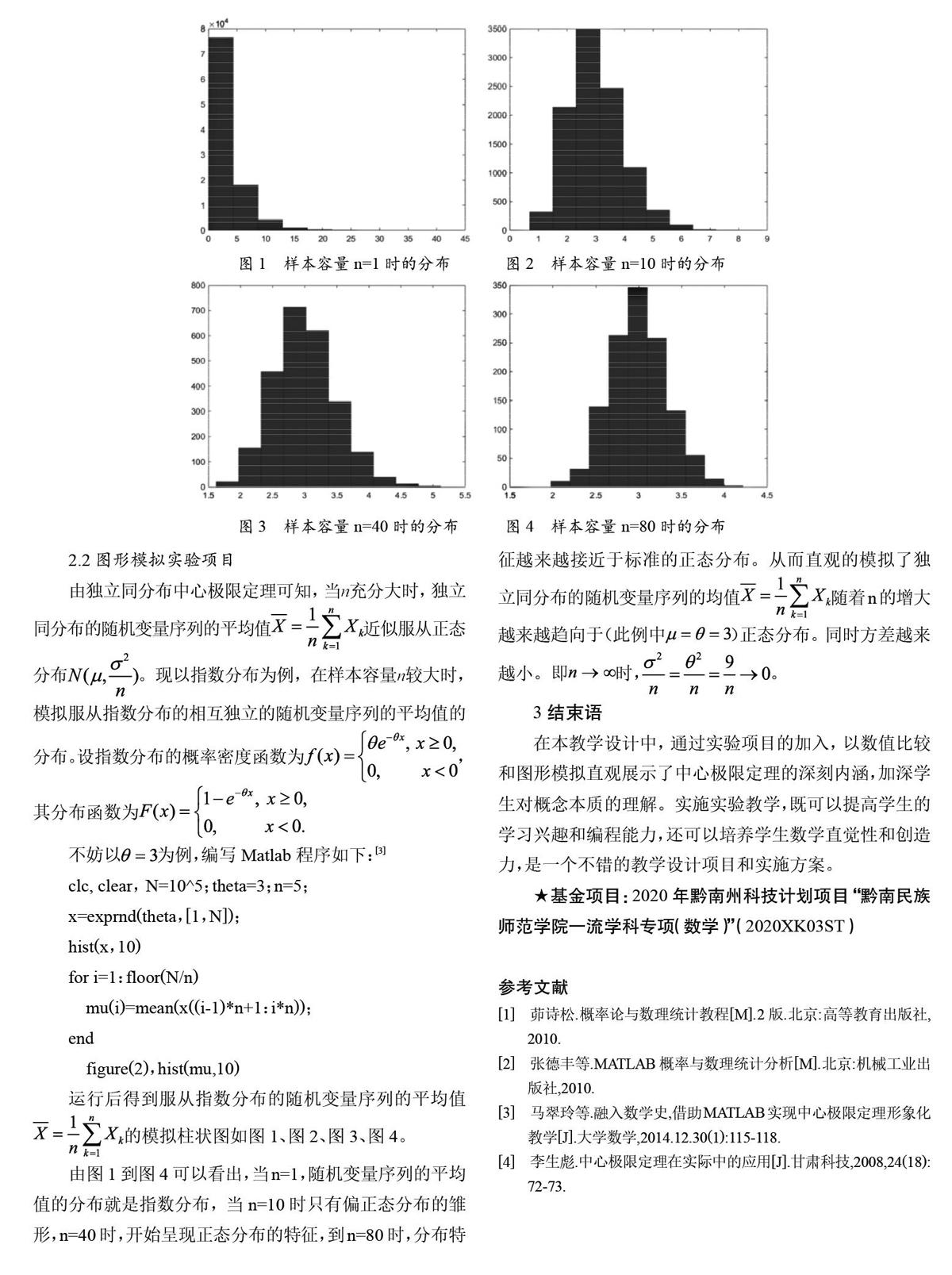
2.2 图形模拟实验项目

由独立同分布中心极限定理可知，当充分大时，独立同分布的随机变量序列的平均值近似服从正态分布。现以指数分布为例，在样本容量较大时，模拟服从指数分布的相互独立的随机变量序列的平均值的分布。设指数分布的概率密度函数为，其分布函数为

不妨以为例，编写Matlab程序如下：[3]

clc， clear， N=10^5;theta=3;n=5;

x=exprnd（theta，[1，N]）;

hist（x，10）

for i=1：floor（N/n）

mu（i）=mean（x（（i-1）*n+1：i*n））;

end

figure（2），hist（mu，10）

运行后得到服从指数分布的随机变量序列的平均值的模拟柱状图如图1、图2、图3、图4。

由图1到图4可以看出，当n=1，随机变量序列的平均值的分布就是指数分布，当n=10时只有偏正态分布的雏形，n=40时，开始呈现正态分布的特征，到n=80时，分布特征越来越接近于标准的正态分布。从而直观的模拟了独立同分布的随机变量序列的均值随着n的增大越来越趋向于（此例中）正态分布。同时方差越来越小。即时，。

3 结束语

在本教学设计中，通过实验项目的加入，以数值比较和图形模拟直观展示了中心极限定理的深刻内涵，加深学生对概念本质的理解。 实施实验教学，既可以提高学生的学习兴趣和编程能力，还可以培养学生数学直觉性和创造力，是一个不错的教学设计项目和实施方案。

基金项目：2020年黔南州科技计划项目“黔南民族师范学院一流学科专项（数学）”（2020XK03ST）

参考文献

[1] 茆诗松.概率论与数理统计教程[M].2版.北京：高等教育出版社，2010.

[2] 张德丰等.MATLAB概率与数理统计分析[M].北京：机械工业出版社，2010.

[3] 马翠玲等.融入数学史，借助MATLAB实现中心极限定理形象化教学[J].大学数学，2014.12.30（1）：115-118.

[4] 李生彪.中心极限定理在实际中的应用[J].甘肃科技，2008，24（18）：72-73.