调频率自适应匹配线性变换及其对旋转机械故障诊断研究

花泽晖 石娟娟 王艳芳 江星星 沈长青 朱忠奎

摘要： 旋转机械常处于变转速工作状态，因而其振动信号也表现出非平稳性。分析此类非平稳信号时由于受有限的时频分辨率影响，常无法获得理想的时频表示，难以揭示与旋转机械健康状态相关的有用信息。根据单个线性调频变换（LCT）能提升特定时刻时频聚集性这一特点，提出了调频率自适应匹配线性变换（Adaptively Matching Chirp?rate Linear Transform， AMCLT）。利用最大峭度准则指导选取每个时刻合适的调频率，并且只保留与所选调频率相关的时频分布用于构造最终的时频表示;扩展原始线性变换基函数，使所提AMCLT方法在无需迭代情况下可同时完成对多分量非线性调频信号的分析。此外，对所提AMCLT方法进行了信号重构分析，可实现对信号中目标频率分量的时域信号重构。振动信号处理结果表明，在时频表示的可读性方面，所提方法可得到能量更加集中且不受交叉项干扰的时频表示;在特征提取方面，所提方法可更加准确地提取旋转机械振动信号中的频率特征，可有效应用于旋转机械的故障诊断。

关键词： 故障诊断; 轴承; 变转速工况; 时频分析; 线性调频变换; 峭度

中图分类号： TH165+.3; TH133.3 文献标志码： A 文章编号： 1004-4523（2021）05-1053-11

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.020

引 言

旋转机械被广泛用于各个行业，而旋转机械系统中关键零部件如齿轮和轴承一旦发生故障，将直接影响系统的安全运行，严重时还会造成经济损失并引发安全事故，因此旋转机械健康状态监测具有非常重要的现实意义。旋转机械的故障诊断主要分析设备运转中所获取的振动信号，然后从信号提取出与故障相关的特征并最终用于故障诊断决策[1?3]。在变转速工况下对旋转机械振动信号进行时频分析可有效揭示信号的时频特征。然而，由转速变化而导致的时频模糊等问题使特征提取困难。为准确地从非平稳振动信号中提取出与故障相关的特征，需要提出有效的时频分析方法来提升时频表示的可读性并得到更加精确的频率估计，并根据提取的瞬时频率脊线诊断旋转机械关键零部件健康状态[1]。经典的时频分析方法如短时傅里叶变换（STFT），小波变换（WT），和维格纳?威尔分布（WVD）等，这些方法被广泛用于非平稳信号处理[4]。但是，这些方法仍存在一些不足，如STFT因测不准原理和有限的时频分辨率影响，不能同时在时间和频率方向上得到理想的分辨率。为解决时频模糊问题，常采用信号分解方法来实现降噪或提取微弱特征。采集的实际振动信号常包含多个频率成分，如轴承内圈故障信号除噪声外还包含转速和内圈故障及转速调制等。典型的信号分解方法，如经验模态分解（EMD），集成经验模态分解（EEMD），局部均值分解（LMD）和变分模态分解（VMD）等。这些方法将原信号分解成多个模态，然后对单个模态分析可更有效辨识故障特征相关的频率分量并完成故障诊断[5]。但在变转速工况下，旋转机械振动信号中的频率分量可能在所选频带内存在模态混叠，这时通过带通滤波则无法分解出不同的频率分量[6]。为提升变转速信号时频表示的可读性，Peng等[7]提出用多项式来表示线性基函数的多项式调频变换（PCT）。PCT通过估计信号的完整瞬时频率，修正基函数以匹配信号频率变化从而提升能量聚集性。而这一方法也存在限制，因PCT中多项式基函数是固定的，即该变换在每个时频点对信号进行特定调频率的调频变换，因此更适合处理仅包含单个频率分量或各频率分量仅在频率方向上发生频移的多分量信号。上述线性变换基函数修正方法可统称为参数化时频分析方法（PTFA），即对时频分析方法中的基函数进行参数化分析以匹配信号时变的频率特征[8]。

此外，时频重排方法也被广泛研究并用于旋转机械健康状态监测，这类方法旨在对时频表示进行能量重分配从而解决时频模糊问题。重分配的关键在于使分配后的时频能量集中在目标时频脊线周围，从而提升时频表示的能量聚集性。如Auger等[9]提出的重分配（RM）方法和Daubechies等[10]提出的同步壓缩变换（SST）。RM同时沿时间轴和频率轴方向对信号能量进行重排，而SST仅沿频率轴方向，由此保留信号的重构性能。但当信号瞬时频率快变时，其在时频图中的能量相比频率恒定时更为分散，从而易导致最终时频结果不够清晰。为解决上述问题，广义解调（GD）和SST相结合的方法被成功用于变转速旋转机械的故障诊断，其关键在于GD可提升时频能量，然后对提升后的时频表示进行重分配，可缓解时频模糊问题并得到精确的瞬时频率估计[11?12]。与GD增强时频聚集性类似，线性调频变换（LCT）对时频图的提升在于调整线性变换基函数来匹配频率变化趋势（STFT的基函数平行于时间轴，适合频率不随时间变化的信号），从而提升能量聚集性[13]。考虑到单个LCT只能增强特定调频率处的时频表示，在分析频率非线性变化的信号时，无法同时增强所有时刻的时频聚集性。Yu等[14]提出广义线性调频变换（GLCT），通过不同调频率的LCT以匹配信号中频率的变化趋势，然后在叠加每个时频点最大的幅值得到最终分析结果。虽然GLCT方法能提升目标脊线处的能量，但同时因保留不恰当调频率的分析结果，使得时频图存在交叉项干扰。当分析信号中频率分量相距较近或包含较多噪声时，时频表示的可读性有待进一步提升。

本文提出了一种新的方法——调频率自适应匹配线性变换（AMCLT）来缓解时频图中的交叉项干扰问题。AMCLT将原始信号分割成若干段以分析信号在各时间段内的频率变化趋势。考虑到时频交叉干扰由不恰当调频率引起，提出谱峭度指导的调频率自适应选择策略，避免人为干预和对先验知识的依赖。扩展原先的线性变换基函数使所提AMCLT方法同时增强谐波多分量信号中的各分量的能量聚集性。通过在同一时刻仅保留合适调频率的时频分布然后再组合即可得到最终分析结果。

1 调频率自适应匹配线性变换（AMCLT）

所提的AMCLT通过使用不同调频率来提升时频表示聚集性并缓解GLCT中的时频模糊问题。本文提出谱峭度指导的调频率选择策略，可减轻时频图中由不合适的调频率引起的交叉干扰[14]。

1.1 线性调频变换分析

LCT得到的时频表示是沿着特定调频率方向分布的，只要调频率与信号频率变化不一致，就会导致时频模糊。为表征不同的变化趋势，GLCT使用了一系列变化的调频率。然而，当信号的各频率分量相距较近或信号噪声能量高时，时频交叉项干扰严重影响其结果的可读性。因此，不恰当调频率导致的问题有待进一步分析和解决。考虑调频率的信号时频表示可写成

当调频率与真实瞬时频率变化一致时，可获得最大的时频聚集性。类似地，当所选的调频率与真实值不一致时，则会在时频表示中引起额外的时频模糊问题。结合GLCT中的幅值叠加算法，其中，为GLCT增强后的时频表示;所选调频率c′由时频表示的最大幅值指导选取，即[14]。不合适的调频率所导致的交叉干扰本质上与采用STFT分析快变信号在时频表示中引起的交叉项是一致的。

定义一仿真信号如下

将该仿真信号的采样频率设为100 Hz，持续2 s。信号的瞬时频率先增大然后保持不变。所提AMCLT方法的时频表示如图1（a）所示。STFT， LCT，GLCT的结果分别如图1（b）?（d）所示，其中，LCT所用调频率为15。从图1（b）?（c）可以看出，在调频率与频率变化趋势一致时，可得到更高的时频聚集性（将STFT看成是调频率为0的LCT）;同样，当调频率不合适时，则会在时频表示中导致一定的交叉干扰。在图1（d）中，GLCT方法得到了能量相对集中的时频表示，但时频表示的可读性仍有待进一步提升。通过对比，所提AMCLT方法在仅保留合适的调频率的结果下，能有效消除由不合适调频率引起的交叉项干扰并提升时频表示的可读性。

1.2 调频率自适应匹配线性变换

LCT中的調频率可看成是某一时刻时频曲线的斜率。先假设一个频率变化的信号x（t），写成

扩展后的基函数中额外引入一个解调因子，与LCT中引入调频率的线性变换基函数表达式相同。LCT中变化的参数为c（τ），LCT中的线性基函数在t=τ处的每个时频点（τ，ω）都对信号进行了相同的调频变换，调频率为c（τ），此时得到的线性变换基函数是相互平行的，适合处理单分量或仅在频率方向发生频移的多分量信号;而所提方法在t=τ处的每个时频点（τ，ω）都对信号进行了调频率变化的调频变换，对应的调频率为（其中，ω为频率索引，而），旨在使用同一角度同时匹配多个频率分量的频率变化趋势。将式（11）扩展后的基函数代入式（8），即可得到考虑相应解调因子的时频表达式

式（12）表明，时频图的幅值受到调频率的影响。同时考虑式（2）和（12），在每个时频点处，若对应的解调因子是由真实的瞬时频率所构建，时频表示的幅值将会达到最大，即能量最集中。但是，由于实际应用中信号瞬时频率相关的先验知识有时无法提前获取，从而难以计算出正确的解调因子来增强时频表示。为解决这一问题，对式（11）中提到的解调因子进行离散化，然后根据最大谱峭度指导的调频率自适应选择策略，并只将所选取调频率对应的变换结果用于最后的时频表示以减轻时频图中的交叉项干扰。根据前述分析，当调频率与真实值越接近，时频脊线的能量越集中，峭度就越大;因此，最优的调频率可根据最大的峭度来确定

式中 kurtosis（?）代表对应时刻时频表示计算的峭度。遍历所有时刻，针对每段截取信号均可选取最优的调频率，组合每个调频率对应的时频分布便可得到最终结果。通过仅保留合适调频率及对应的时频分布可缓解GLCT中不合适的调频率在时频表示中引起的交叉项干扰从而提升时频表示的可读性。

为确定调频率可选择的范围并尽可能多的包含合适的调频率，引入正切函数对调频率加以约束。同时，也因为正切函数反映了时频脊线的倾斜角度，也可以反应曲线的变化趋势，且正切函数一个周期内对应的角度具有确定的范围。为此，引入一个新参数α（t），写成

式中 N决定了离散的角度α的个数与变化步长。特别地，当N=1，所提AMCLT的时频表达式等同于标准的STFT。随着N的增大，所估计的调频率的精度会提高，但同时会增加方法的实际运算时间。所提AMCLT的表达式最终可被写成

所提AMCLT算法的主要流程如图2所示。

1.3 信号重构

作为时频分析方法的一个重要特性，AMCLT方法应满足对信号中目标频率分量的重构性能。根据改进后的时频表示可恢复原先时域信号，证明如下

式中 代表所提AMCLT算法改进后的时频表示，w（t）代表截取信号的窗函数，w（0）为由窗函数定义的常数。对多分量信号，只要正确地分离出目标频率分量，多分量信号中各频率分量均可被单独重构，写成

仿真信号的采样频率均设为200 Hz，持续4 s。用所提的方法重构该多分量信号，结果如图3所示，重构出来的信号时域波形与原先的信号变化趋势一致。为量化重构结果的准确性，计算得到的信号重构平均相对误差（MRE）为3.36%，说明多分量信号被准确重构出来[16]。同时还研究了该多分量信号中的单分量重构，各分量重构结果如图3（b）?（d）所示，分别对应信号中的频率分量f（t）及其倍频。

为进一步分析所提方法在不同信噪比下重构信号的能力，研究了不同噪声能量下的信号重构结果，输入信号的信噪比从0变化至20 dB，结果如图4所示。随着信号中噪声能量的降低，所有方法都能重构出更加精确的结果，所提AMCLT方法与STFT和PTFA相比，重构出的信号有更高的信噪比;与GLCT相比，AMCLT在低信噪比（0?8 dB）时重构的信号信噪比更高，并在信噪比大于10 dB时能得到和GLCT相近的结果。所提方法在估计得到目标时频脊线后，可重构出原先的时域信号波形，保证了旋转机械振动信号中故障特征的准确提取，可为后续的故障诊断提供基础。

1.4 瞬时频率估计

瞬时频率估计的准确性也是衡量时频表示的重要指标。同时，瞬时频率也是变转速下旋转机械故障诊断不可或缺的信息。通常，可根据所提取的瞬时频率之间的比值计算故障特征系数并根据所计算得到的系数判断旋转机械具体的故障类型，因为故障特征系数由轴承或齿轮本身的参数决定，不随转速的变化而变化。本节采用峰值搜索算法估计瞬时频率，分析和比较不同方法得到的时频脊线的准确性[17]。与1.3节信号重构相同，分析了不同信噪比下多分量信号的瞬时频率估计。峰值搜索算法中瞬时频率估计可写成

式中 IFR（t）表示真实的瞬时频率。对信噪比从0变化到20 dB的信号进行瞬时频率估计，所选用分析的多分量信号由式（21）和（22）定义。

分析时，PTFA中涉及的基函数参数设置成与瞬时频率f（t）一致，离散的角度个数设为30，分析结果如图5所示。图中可看出，AMCLT方法提取的瞬时频率整体上有最小的MRE，说明所提方法在分析多分量信号时拥有较好的抗噪性能，能提升瞬时频率估计的准确性。GLCT和PTFA在信号仅包含少量噪声时，可以得到精确的瞬时频率估计，但随着噪声的增加，所得MRE相比所提方法偏大，其原因在于：PTFA没有同时匹配信号中所有分量的变化趋势，而GLCT虽然增强了时频表示，但其中不合适的调频率使得时频图存在一定的交叉干扰。由此可得出结论：根据计算的MRE可说明所提AMCLT方法有相对更加稳定的抗噪性能，能提升瞬时频率估计的准确性。

2 仿真分析

为验证所提方法在增强时频表示方面的有效性，对1.3节中定义的仿真信号继续进行分析，对比不同方法所得时频分析结果。同时，还研究了不同信噪比对信号时频表示的影响。

2.1 单分量信号分析

考虑到实际信号常包含噪声，将单分量的信噪比设置为3 dB以模拟实际信号。分析时，所选用的窗长为0.8 s，所提方法和GLCT中离散角度的个数均设为30。

不同方法的分析结果如图6所示。从图6（a）可以看出，STFT结果仅在2 s前后有较集中的能量。在图6（b）?（d）中，GLCT， PTFA及所提方法通过匹配信号频率变化，与STFT相比均能有效提升时频表示的能量聚集性。

2.2 多分量信号分析

在工程实际中，旋转机械的振动信号通常包含多个频率分量，同时在不涉及迭代的情况下同步增强多个频率分量的能量聚集性可进一步简化算法，对旋转机械的振动信号处理具有重要意义。为了验证AMCLT处理多分量信号时的有效性，对式（21）定义的多分量信号进行分析，并比较不同方法的分析结果。

时频分析方法（STFT，GLCT及PTFA）的结果如图7（a）?（c）所示，所提AMCLT的结果如图7（d）所示。与单分量信号分析结果类似，STFT的结果在0?1 s和3?4 s内得不到较能量集中的时频表示，且在部分时刻在频率分量2f（t）及3f（t）之间存在一定的交叉干扰。GLCT能得到较高的聚集性，但同样地在相邻频率之间存在由不匹配的调频率引起的时频交叉问题，影响时频表示的可读性。PTFA方法因仅匹配了该多分量信号中的单个频率成分（图中，PTFA的基函数设置与公式（22）定义的f（t）一致），并不能同时增强所有频率分量的聚集性，如频率分量3f（t）存在的时频模糊问题。图7（d）中，AMCLT可以获得能量与GLCT接近的时频表示，所提的角度自适应选择策略可有效缓解时频表示中的交叉项干扰，从而得到更加清晰的时频表示。在该信号分析中，所有方法的分析窗长均被设置为0.8 s。

在多分量信号中加入适量噪声再次分析，结果如图8所示。在图8（a）和（c）中，可以发现，目标时频脊线在信号两端出现了中断，表明分析方法在该时刻未能正确揭示信号的频率变化。在图8（b）和（d）中，由GLCT获得的时频图比较完整地揭示出了频率分量的变化趋势，但由噪声引起的时频交叉项相比不含噪声时更加明显，而AMCLT通过仅保留合适的调频率及对应的时频分布有效提升了所得时频表示的可读性。

对图8所得时频表示分别进行瞬时频率估计，提取的瞬时频率脊线如图9所示。图中，STFT， GLCT及PTFA方法在提取信号两端的瞬时频率脊线时，均存在一定误差，而所提方法可准确提取出目标频率脊线，说明所提方法在增强时频表示的同时还能有效提升所估计瞬时频率脊线的准确性。变转速下旋转机械故障类型是根据所提取的瞬时频率脊线诊断的，更准确的瞬时频率脊线说明所提方法具有处理变转速下旋转机械振动信号的潜力。

继续添加适量噪声，将信噪比设为0再次分析。不同方法的结果如图10所示。从图中可以看出，随着噪声的增加，STFT及PTFA的分析结果中时频脊线不连续，而所提方法在减轻GLCT中交叉干扰的同时能得到相对更加清晰的时频表示，结果如图10（d）所示。

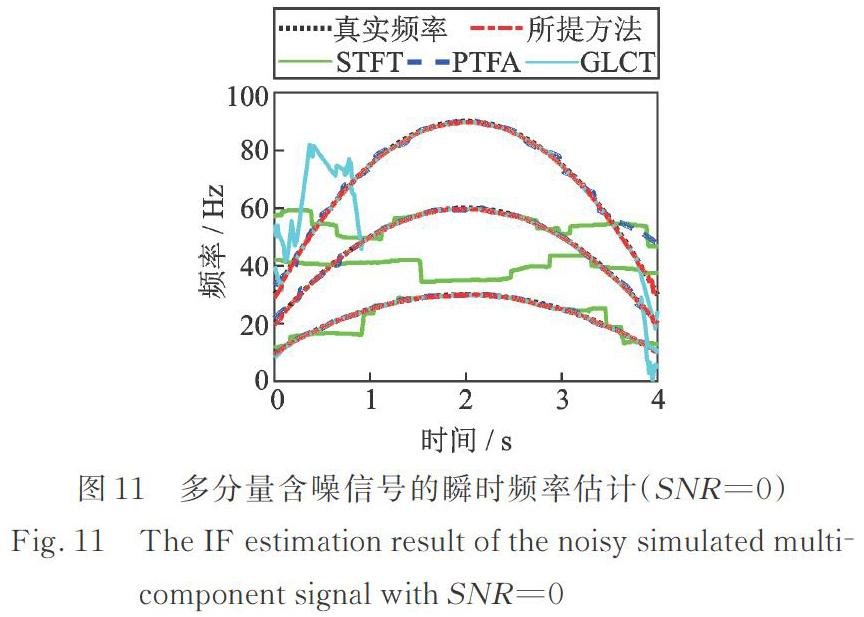
根据信噪比为0所得时频表示估计瞬时频率，估计的瞬时频率脊线结果如图11所示。STFT的结果仅在2 s左右估计出f（t）及2f（t）对应的时频脊线。从图中还可以看出，所提方法仍能得到精准的瞬时频率估计，体现了所提方法比其他方法具有更强的抗噪性能。

3 实验验证

为进一步验证AMCLT算法处理旋转机械振动信号的有效性，分别利用行星齿轮箱振动信号和轴承故障实验台振动信号进行处理和结果分析，并以此诊断行星齿轮箱和轴承的健康状态。

3.1 行星齿轮箱振动信号分析

行星齿轮箱振动信号采集自模拟风电齿轮箱模拟试验台，如图12所示[19?21]。由安装在行星齿轮箱箱体上的加速度计采集得到实验数据。采样频率设为20 kHz。电机旋转频率大约从40 Hz增加到60 Hz，然后再减少到40 Hz。齿轮箱的配置如表1所示，磨损的齒轮如图13所示。根据齿轮箱的配置[21]，计算了行星齿轮箱的特征频率，如表2所示，其中fd表示电机变化的旋转频率。

该行星齿轮箱的振动信号如图14（a）所示，电机转速（fd）的变化如图14（b）所示。STFT和所提方法分析结果分别如图14（c）?（d）所示。对比结果，可以发现所提方法能够得到更加清晰的时频脊线。该振动信号的瞬时频率估计结果如图15所示，图中STFT与AMCLT提取的脊线分别与真实频率的对比进一步说明了AMCLT在增强时频表示的同时还能提升所估计瞬时频率的准确性。在分析该振动信号时，选取的窗长为1.5 s。结合图14（c）和15，可发现该振动信号中最主要的频率成分为电机的转频fd及其谐波，但这些转频分量并不能用于揭示行星齿轮箱的健康状态。除转频成分外，还可观测到啮合频率fmesh1及其边频带fmesh1-2fsun1，这些频率分量表明该行星齿轮箱中太阳轮存在故障。

3.2 轴承内圈故障振动信号分析

與齿轮箱的故障诊断有所区别，变转速下轴承故障类型的诊断由轴承的故障特征系数（FCC）来决定。轴承的故障特征系数由轴承本身的规格参数所决定，不随转频的变化而变化，轴承的瞬时故障特征频率fIFCF和轴转频fISRF间的关系为：fIFCF=FCC×fISRF。轴承运行在变转速工况下时，无法通过频谱分析观测到故障特征频率等峰值存在。因此，需要从时频图提取瞬时频率脊线，计算其相互之间的比值，并判断各比值与故障特征系数FCC的关系，从而开展变转速轴承的故障诊断。

轴承的振动信号采集实验台如图16所示。该实验台为SpectraQuest机械故障模拟器（MFS?PK5M），由电机控制安装着滚动轴承（ER16K）的轴转动，试验台中左边的轴承是健康的，右边的轴承在内圈上有局部缺陷。电机的转速由交流驱动器控制，由加速度计记录轴承的振动数据，同时还使用了编码器（EPC型号775）来测量转速，即瞬时旋转频率（fISRF）。实验轴承的参数如表3所示，计算出轴承的FCC为5.43，表明该振动信号中瞬时故障特征频率fIFCF=5.43fISRF。

轴承内圈实验信号的采样频率设置为200 kHz，持续10 s。采集的振动信号如图17（a）所示，转速变化如图17（b）所示。采用STFT， GLCT和AMCLT对包络信号进行分析（窗长设置为1 s），结果分别如图17（c）?（e）所示。可以看出，AMCLT和GLCT时频图中时频脊线相比STFT有更高的能量聚集性。利用局部峰值搜索算法提取瞬时频率，结果如图17（f）所示。所提方法提取的瞬时频率脊线与真实频率基本吻合;而STFT中提取的部分脊线在7?10 s内有较大的估计误差。GLCT方法经匹配调频率完整地识别出了前3阶故障特征频率对应的时频脊线，但在提取时频图中能量较低的频率分量时，因时频交叉干扰存在较大的估计误差，如在提取2阶轴转频和故障特征频率时。因此通过对比可得出结论，本文所提出的AMCLT方法可以增强轴承振动信号的时频表示并提高目标时频脊线提取的准确性，有助于准确判断轴承的故障类型。所提取的各瞬时频率脊线之间的比值见表4。

根据表4可以发现前3阶故障特征频率fIFCF与瞬时旋转频率fISRF的比值分别为（记为向量R1），正好和故障特征频率及其2倍和3倍频分别与轴瞬时旋转频率的比值一致，即分别对应轴承内圈故障特征系数（FCC=5.43）及其2倍和3倍。同样，前3阶故障特征频率fIFCF与第2阶瞬时旋转频率2fISRF的比值分别为[]（记为向量R2），分别对应故障特征频率及其2倍和3倍频与轴瞬时旋转频率的2倍频的比值。并且所有计算得到的比值与对应的故障特征系数的MRE均小于3 %。此外，在第1阶故障特征频率fIFCF周围还可观察到转速调制现象。因此，可得出结论，该轴承存在内圈故障。以上结果表明，所提出的AMCLT方法可成功应用于诊断轴承的故障类型。

4 结 论

本文针对变转速工况下旋转机械振动信呈现出非线性和故障特征信息难以提取的问题，提出了调频率自适应匹配的线性变换（AMCLT），用于解决信号时频表示中存在的频谱模糊问题并减轻时频图中的交叉项干扰。提出了峭度指导的调频率自适应选择策略，并对线性变换的基函数进行扩展，在不需要迭代的情况下同步提升多分量信号的时频聚集性。在峭度指导下，选择与各信号段瞬时频率轨迹最匹配的角度（调频率），避免了对瞬时频率先验知识的依赖。由此，可自适应地选择最优的调频率来匹配信号的时频特征，同时消除不合适的调频率干扰从而减轻时频表示中的交叉项干扰。此外，还研究了所提出AMCLT算法对信号中目标频率分量的重构性能，重构结果表明所提方法具有相对平稳的抗噪声干扰能力。对不同时频分析方法的时频图进行瞬时频率估计，发现该方法可有效提升时频表示的可读性和瞬时频率提取的准确性。通过对行星齿轮箱和轴承的振动信号处理，AMCLT算法可以提取出故障特征相关信息，准确地诊断出旋转机械关键零部件的健康状况。同时也验证了该方法在变转速工况下旋转机械健康状态监测中的有效性。

参考文献：

[1] Feng Z， Liang M， Chu F. Recent advances in time-frequency analysis methods for machinery fault diagnosis： A review with application examples[J]. Mechanical Systems and Signal Processing， 2013， 38（1）： 165-205.

[2] 石娟娟， 王 林， 罗春艳， 等. 基于优化最小算法的齿轮箱复合故障特征稀疏表示 [J]. 振动工程学报， 2017， 30（6）： 1045-1055.

Shi Juanjuan， Wang Lin， Luo Chunyan， et al. Sparse representation for gearbox compound fault feature extraction based on majorization-minimization algorithm[J]. Journal of Vibration Enginering， 2017， 30（6）： 1045-1055.

[3] Wang S， Chen X， Selesnick I W， et al. Matching synchrosqueezing transform： A useful tool for characterizing signals with fast varying instantaneous frequency and application to machine fault diagnosis[J]. Mechanical Systems and Signal Processing， 2018， 100： 242-288.

[4] Yan R， Gao R X， Chen X. Wavelets for fault diagnosis of rotary machines： A review with applications[J]. Signal Processing， 2014， 96： 1-15.

[5] Jiang X， Shen C， Shi J， et al. Initial center frequency-guided VMD for fault diagnosis of rotating machines[J]. Journal of Sound and Vibration， 2018， 435： 36-55.

[6] 王天楊， 李建勇， 程卫东. 基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断 [J]. 振动与冲击， 2014， 33（18）： 7-13.

Wang Tianyang， Li Jianyong， Cheng Weidong. Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum[J]. Journal of Vibration and Shock， 2014， 33（18）： 7-13.

[7] Peng Z K， Meng G， Chu F L， et al. Polynomial chirplet transform with application to instantaneous frequency estimation[J]. IEEE Transactions on Instrumentation and Measurement， 2011， 60（9）： 3222-3229.

[8] Yang Y， Peng Z K， Dong X J， et al. General parameterized time-frequency transform[J]. IEEE Transactions on Signal Processing， 2014， 62（11）： 2751-2764.

[9] Auger F， Flandrin P， Lin Y-T， et al. Time-frequency reassignment and synchrosqueezing： An overview[J]. IEEE Signal Processing Magazine， 2013， 30（6）： 32-41.

[10] Daubechies I， Lu J， Wu H-T. Synchrosqueezed wavelet transforms： An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis， 2011， 30（2）： 243-261.

[11] Li C， Sanchez V， Zurita G， et al. Rolling element bearing defect detection using the generalized synchrosqueezing transform guided by time?frequency ridge enhancement[J]. ISA Transactions， 2016， 60： 274-284.

[12] Shi J， Liang M， Necsulescu D-S， et al. Generalized stepwise demodulation transform and synchrosqueezing for time-frequency analysis and bearing fault diagnosis[J]. Journal of Sound and Vibration， 2016， 368： 202-222.

[13] Mann S， Haykin S. The chirplet transform： Physical considerations[J]. IEEE Transactions on Signal Processing， 1995， 43（11）： 2745-2761.

[14] Yu G， Zhou Y. General linear chirplet transform[J]. Mechanical Systems and Signal Processing， 2016， 70： 958-973.

[15] Guan Y， Liang M， Necsulescu D S. Velocity synchronous linear chirplet transform[J]. IEEE Transactions on Industrial Electronics， 2019， 66（8）： 6270-6280.

[16] Zhu X， Zhang Z， Li Z， et al. Multiple squeezes from adaptive chirplet transform[J]. Signal Processing， 2019， 163： 26-40.

[17] 张 杰， 史治宇. 应用小波时频脊提取和自适应滤波进行时变系统参数识别[J]. 振动工程学报， 2019， 32（3）： 462-470.

Zhang Jie， Shi Zhiyu. Parameter identification of time-varying structures by using wavelet ridge extraction and adaptive filtering[J]. Journal of Vibration Enginering， 2019， 32（3）： 462-470.

[18] 雷亚国， 何正嘉， 林 京， 等. 行星齿轮箱故障诊断技术的研究进展 [J]. 机械工程学报， 2011， 47（19）： 59-67.

Lei Yaguo， He Zhengjia， LIN Jing， et al. Research advances of fault diagnosis technique for planetary gearboxes[J]. Journal of Mechanical Engineering， 2011， 47（19）： 59-67.

[19] 陈小旺， 冯志鹏， LIANG Ming. 基于迭代广义同步压缩变换的时变工况行星齿轮箱故障诊断[J]. 机械工程学报， 2015， 51（1）： 131-137.

Chen Xiaowang， Feng Zhipeng， Liang Ming. Planetary gearbox fault diagnosis under time-variant conditions based on iterative generalized synchrosqueezing transform[J]. Journal of Mechanical Engineering， 2015， 51（1）： 131-137.

[20] Guan Y， Liang M， Necsulescu D S. A velocity synchrosqueezing transform for fault diagnosis of planetary gearboxes under nonstationary conditions[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2016， 231（15）： 2868-2884.

[21] 秦嗣峰， 冯志鹏， LIANG Ming. Vold-Kalman滤波和高阶能量分离在时变工况行星齿轮箱故障诊断中的应用研究 [J]. 振动工程学报， 2015， 28（5）： 839-845.

Qin Sifeng， Feng Zhipeng， Liang Ming. Application of Vold-Kalman filter and higher ordr energy separation to fault diagnosis of planetary gearbox under time-varying conditions[J]. Journal of Vibration Enginering， 2015， 28（5）： 839-845.

作者简介： 花泽晖（1996-），男，硕士研究生。E-mail： zhhua163@stu.suda.edu.cn

通訊作者： 石娟娟（1985-），女，博士，副教授，硕士生导师。E-mail： jshi091@suda.edu.cn