采用加速度整形与力矩补偿的柔性连杆振动抑制方法

徐建明 万准生 董建伟 马益普

摘要： 针对负载柔性连杆在加速，减速和停止阶段会发生残余弹性振动的现象，研究一种滚珠丝杆驱动柔性连杆的振动抑制方法。采用频率激励法和最小二乘法辨识柔性连杆加速度固有谐振频率和电机滚珠丝杆驱动柔性连杆系统动力学模型参数：转动惯量和摩擦系数。在此基础上采用输入整形法规划加速度信号，降低规划的加速度信号中柔性连杆的固有谐振频率区域内信号幅值，以避免激励固有谐振。根据柔性连杆动力学模型估计连杆加速度信号，采用广义最小方差控制方法，设计柔性连杆振动抑制控制器输出谐振力矩补偿信号，以此来抑制运行过程中连杆弯曲变形产生的振动。最后在搭建的滚珠丝杆滑块驱动柔性连杆的实验平台上进行实验，实验结果验证了所研究方法的有效性。

关键词： 振动抑制; 柔性连杆; 加速度整形; 广义最小方差

中图分类号： TB535; TH113.1 文献标志码： A 文章编号： 1004-4523（2021）05-1027-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.017

引 言

设备振动产生的原因多种多样，比如机械刚性较差;运行的频率高、速度快、加速时间短，运动方向改变时，产生惯性冲击。针对这些问题国内外学者提出许多方案，大致分为两个方面，一方面，从能量的角度考虑，重新规划跟踪轨迹，包含加速度，速度和位移的规划。用输入整形法规化输入信号长久以来是学者的研究重点，近年来得到很大的发展。例如在时域的情况下根据系统的脉冲响应，Singhose[1]，Mohamed等[2]提出了一种经典的脉冲整形法，通过设计脉冲信号与原信号进行卷积，使得脉冲激起的振动相互抵消达到零振动的目的。由于脉冲整形法存在一定的时延，因此李琳等[3]，Zhao等[4]考虑对原轨迹先进行均匀加速，加速后轨迹时间缩短，然后对加速后的轨迹用脉冲整形法整形，使得整形后的轨迹没有延時并且达到零振动效果。Stanislao等[5]针对负载可变，固有频率变化的系统，运用神经网络训练预测变化的固有频率，结合脉冲整形规划信号，实时整形信号抑制振动。Biagiotti等[6]另辟蹊径，考虑用特定的指数滤波器对加速度轨迹进行优化，从而使得系统残余的振动量最小。陈特欢等[7]采用遗传算法优化轨迹，使得系统弹性振动能量最小，从而抑制系统产生的振动。在频域的情况下根据系统的频率响应，Kim等[8]用均值滤波和脉冲整形法对轨迹进行优化，抑制设备振动。Li等[9]考虑到原始轨迹由不同频率谐波信号叠加组成，减小信号中与设备固有频率相同的谐波信号幅值，从而减弱振动。方波信号由不同频率的谐波信号组成，Meckl等[10?12]减小方波信号中含谐振频段的谐波信号幅值，整形为类方波信号，再结合一定的控制方法，提高系统的抗干扰能力。另一方面，也有学者运用控制方法抑制残余振动。Qiu等[13?15]考虑用广义最小二乘法抑制振动。马驰骋等[16]对于单自由度变质量的柔性梁运用LQR控制器抑制梁顶部的振动。输入整形法和抑振控制方法分别从避免激励固有谐振频率和主动抑振控制角度来降低系统振动幅值，但输入整形法需要已知固有谐振频率，如果运行过程中固有谐振频率发生变化，那么输入整形法抑制振动能力就会变弱;对于滚珠丝杆设备（尤其是“T”型的负载设备）的振动研究表明，谐振频率随着移动位置改变会发生变化。因此，有必要将两者结合，在无加速度传感器测量末端振动加速度情况下，研究基于柔性模型的加速度估计方法，进而研究基于加速度整形与柔性力矩补偿的振动抑制方法，抑制滚珠丝杆驱动柔性连杆运行过程中和结束后的弹性振动，既精确跟踪规划的轨迹，又在起始、停止和运行阶段提高抗振性能和稳定性。

针对滚珠丝杆驱动柔性连杆运行过程中会产生颤振的情况，采用频率激励法和最小二乘法辨识柔性连杆加速度固有谐振频率和电机滚珠丝杆驱动柔性连杆系统动力学模型参数：转动惯量和摩擦系数;在此基础上采用输入整形法规划加速度信号，降低柔性连杆的固有谐振频率区域内的规划加速度幅值;建立力与柔性连杆加速度之间的自回归滑动离散模型，以此估计柔性连杆顶端的加速度信号，设计性能指标代价函数，使规划的加速度与估计的加速度方差最小，根据此函数设计出最小广义方差控制律，抑制在跟踪规划的位移信号过程中产生的振动，最后在搭建的滚珠丝杆滑块驱动柔性连杆的实验平台上进行实验。实验结果表明：在启动和停止阶段，柔性连杆的振动幅值的均方根值在0.2 m/s2之内，加速、减速过程中的柔性连杆最大振动幅值均方根值为0.4 m/s2，从而验证所研究方法的有效性。

1 滚珠丝杆驱动的机械系统建模

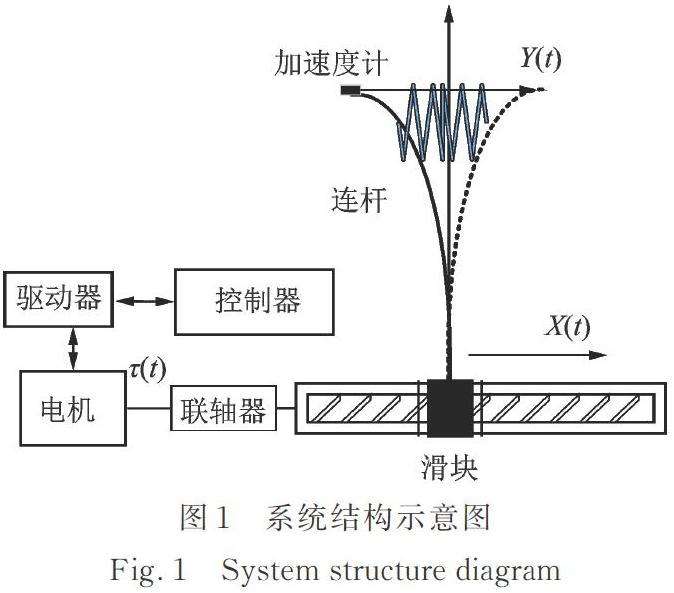
滚珠丝杆驱动的机械系统的整体机械结构由两部分组成，一部分是刚性部件，由伺服电机、联轴器、滚珠丝杆、直线导轨和滑块工作台组成。刚性部件的驱动力由伺服电机提供，经过滚珠丝杠转化为刚性位移量，在运动过程中忽略库伦摩擦的影响，只考虑黏性摩擦的作用，且不考虑滚珠丝杆轴向振动和旋转产生的振动。另一部分是柔性部分：一个柔性连杆被固定在滑块的底部，连杆的顶部安装一个加速度计，测量运动过程中的加速度，用于实验检验与分析，系统结构示意图如图1所示。

根据振动模态叠加和机电特性，将系统描述为单输入?两输出模型，输入是电机驱动力矩信号，输出是底部滑块的位移量和柔性连杆顶部的加速度，系统的模型用传递函数表示为

式中 为总的转动惯量;为黏性摩擦系数，这些参数用最小二乘法辨识，辨识的具体的过程参考文献[17]。

式中 为延时时间; e-rs和为系统的纯延时和机械噪声，它们对系统的影响不容忽视。和为第个弹性振动模态的谐振频率和阻尼比，这两个参数确定电机力矩与柔性连杆顶部加速度的模型，辨识这两个参数至关重要。实验采用的是非参数方法，非参数法需要为研究的系统提供一个激励信号，激励信号应该包含丰富的动态频率特性，正弦扫频信号可以满足系统的需要。

以正弦扫频信号作为输入信号激励系统，以加速度计采集顶端的振动加速度信号，对采集到的时域加速度信号进行离散傅里叶变换，得到振动信号的谐振频率。

阻尼比的辨识采用衰减响应法，柔性连杆顶端的加速度响应由二阶线性系统叠加而成，而二阶线性系统单位脉冲响应[1]的包络线是指数衰减的，因此测得振动加速度响应的指数衰减曲线，根据连续两个峰值与阻尼比之间的关系，可计算出系统的阻尼比[3，18]。为提高计算精度，取几组连续的峰值点，计算各组阻尼比后，再取平均值。

图1中，被控对象为类似字母T型的装置，这一装置的显著特征是底部的滑块带动轻质柔性连杆一起移动，在速度快的情况下，由于存在柔性，连杆产生弹性振动，连杆的顶部与底部滑块的运动不同步，影响定位的精度，因此从两方面考虑来抑制振动，一方面从能量的角度，规划适合系统的加速度、速度信号，避免能量的浪费;另一方面从控制的角度需要实时计算控制补偿量，以此调整振动抑制器的控制量。整体的振动抑制方法将在下节详细介绍。

2 柔性连杆振动抑制策略

针对机械运动过程中存在柔性负载情况，既要快速跟踪设定的位移和速度，又需要有效抑制运动过程中的弹性振动，本节设计一种柔性连杆振动抑制策略，系统结构框图如图2所示。

振动抑制策略包含两部分：1）用输入整形法规划方波加速度信号、速度和位移信号;2）在PID控制器保证位移跟踪的前提下，用柔性振动控制器补偿振动柔性力矩。

对于点到点运动，滚珠丝杆滑块驱动柔性连杆运动过程中，如果用方波加速度规划速度和位移曲线，由于加速度变化剧烈、加速时间短、机械负载或者传动机构有柔性存在，会导致起始和停止阶段加剧柔性连杆振动。采用图2的振动抑制策略，在抑制振动幅值和快速跟踪之间达到平衡，通过加速度整形得到一个既避免激励设备谐振又快速的加速度信号，减缓起始和停止的冲击。在位移相同条件下，跟踪规划的位移曲线，在起始和停止时产生较小的振动;同时，建立柔性模型估計加速度，采用柔性振动抑制环节，减缓控制信号的波动，抑制加减速和换向过程中的柔性振动。

2.1 输入整形法

如果规划的加速度信号包含系统固有谐振频率，那么在柔性连杆运动的起始和停止阶段，会加剧柔性连杆特别是顶端的弹性振动。根据Meckl等[10?12]提供的输入整形方法，输入信号的频谱幅值与残余的加速度信号幅值有关，利用这一关系来构建目标方程

式中 是的傅里叶反变换，为每个升余弦谐波信号的幅值。目标方程（3）的第1项保证加速度的幅值能近似保持方波形式，第2项使得频谱幅值的平方在包含固有谐振频率的频率段内最小化，整体保证在输入信号激励下，系统能量最小化，为求得构造信号升余弦的幅值，需要对目标函数求导[11]，即，求出的值。

根据公式（3）计算构建整形信号各个谐波信号的幅值，构建出的信号避免激励柔性连杆固有的谐振频率，构建目标函数第2项不仅考虑连杆固有的谐振频率，而且考虑时变的谐振频率，使构建的信号在包含固有频率段内幅值最小，由于规划的运动加速度类似为方波加速度，加速时间短。用重新规划的加速度构造信号的位移、速度信号，可更好地完成任务，减小末端点的振动，并且保证其鲁棒性。

2.2 柔性力矩补偿控制

在设计柔性振动控制器之前，需要实时估计加速度值，如公式（2）所示柔性模型由2阶线性模型叠加而成，大量研究表明，低频振动模态是主要因素，因此假设公式（2）中只包含1个弹性振动模态，可表示为

由于加速度计只是用于测量振动信息做实验验证，不用于信号反馈，因此需要基于离散的模型估计实际输出，代替真实的加速度信号，定义误差

要保证稳定性需要确定特征方程（13）的根在单位圆内，只要选择合理，和就可保证系统的稳定性，而且也适合于非最小相位系统，即使多项式不稳定，仍可通过选择合适的和多项式来保证系统特征根在单位圆内。

设计出柔性补偿信号后，输出给电机驱动器的力矩信号由两部分组成

其中前3项为第1部分，表示PID反馈控制;第4项为第2部分，表示基于柔性模型的振动抑制前馈补偿控制。

3 柔性连杆模型辨识和振动抑制实验验证

实验装置硬件平台如图3所示：驱动力部分采用的是欧姆龙电机R88M?K40030H?S2和型号为R88D?KN04H?ECT的驱动器。执行机构采用的是台湾上银科技有限公司生产的单轴直线模组，型号为KK86，导程是10 mm，轨道为总长度440 mm的滚珠丝杆，此型号的滚珠丝杆具有低阻尼、高刚性、传动效率高等特点。柔性连杆的长度为0.5 m，柔性连杆顶部安装加速度计，振动加速度计采用的是秦皇岛鑫辰电子科技有限公司生产的AD2000T，测量范围为0.1?3000 Hz。采集振动加速度信号使用NI模拟采集卡片9205。实验的控制器是一款装有3S软件公司开发的软PLC内核的工控机。

3.1 柔性连杆模态分析和辨识

根据柔性连杆模态理论分析，设计激励信号，进行柔性连杆模型辨识。图3实验装置的连杆参数如表1所示，连杆的弹性模态特征可根据欧拉?伯努利梁理论分析。根据实验装置，梁的模型可简化为一端固定和一端带质量的自由端。悬臂梁的解满足非线性超越方程[20]

针对柔性连杆谐振频率的辨识，设计扫频力矩信号：，在180 时间内扫频范围为1?91 Hz，扫频实验的正弦扫频力矩激励信号和采集的柔性连杆顶端加速度分别如图4和5所示。为显示清晰，图4只显示0?1 。由于加速度信号的时域信号变换到频域后，可得到加速度信号频域的特征，因此通过频谱分析（FFT），采集的加速度信号存在一个谐振峰值，如图6所示，柔性连杆的低阶振动谐振频率为30 Hz。

针对模态阻尼比的辨识，设计方波力矩信号，测得振动加速度自然衰减响应曲线如图7所示，根据文献[3，18]中衰减响应求阻尼比的方法，选取8组相邻波峰值，取平均值，阻尼比为0.0052，计算的包络线表达式为

通過扫频响应曲线频谱分析得到和衰减响应法得到=0.0052，实验过程中采样周期，为保证输入力矩信号与测量的加速度同步，测量延时时间，实验中测量的延时=4 ，则柔性模型表达式（5）为

为了验证模型，柔性模型（5）离散化为自回归滑动模型（8），其中，，=4，;模型验证在Matlab上完成，用方波力矩信号作为输入信号，根据响应曲线验证模型。如图8所示，实线为加速度计采集信号经带通滤波器滤除量测噪声后的实际测量加速度曲线，虚线为基于柔性模型的加速度估计曲线。

3.2 开环模式下输入整形算法实验验证

在开环模式下进行实验，比较方波输入和类方波输入情况下系统的加速度响应。图9表示系统输入的方波力矩信号，作用时间为0?1.2 s。图10为在方波力矩信号的作用下柔性连杆顶端的加速度响应，在1.2 s时撤去作用力矩，顶端振动加速度信号在2.5 s左右加速度减小到零。

根据公式（3），取 λ=16.7，频率 ωi（l=1，2，…，11）分别为：25，26，27，28，29，30，31，32，33，34，35 Hz;计算出公式（4）中 βl（l=1，2，…，15）各个谐波信号的幅值为： 0.0945，0.0945，0.0945，0.0944，0.0938，0.0918，0.0835，0.0230，0.0001，-0.0583，0.0438，0.0652，0.0736，0.0779，0.0804。15个谐波信号构成的力矩信号如图11所示。图12是在类方波力矩信号作用下顶端的加速度响应曲线，作用力持续1.2 s，同样在1.2 s时撤去作用力矩，顶端的加速度幅值在1.5 s 减小到零。通过对比图10和12，说明类方波输入整形法效果更好。普通的方波激励下柔性连杆顶端加速度幅值减小到零需要1.3 s，但是类方波力矩激励下只需要0.3 s，相比方波激励，柔性连杆顶端加速度幅值减小到零的时间缩短1 s。

3.3 基于PID控制下的位移跟踪和广义最小二乘法振动抑制实验

基于柔性模型（7），在保证闭环稳定性的前提下，选取加权多项式，的值，首先确定加权多项式的阶次，然后确定多项式中的参数。具体做法如下：

柔性补偿控制中的加权多项式得到后，还需根据刚性模型得到PID的控制参数，刚性模型是电机力矩与滚珠丝杆滑块位移量之间的传递函数，根据动力学模型表达式（1），需要辨识的参数有两个，转动惯量和黏性摩擦系数，使用最小二乘法辨识[17]两个参数。设计激励信号，辨识的转动惯量为0.56×10-4 kg·m2，黏性摩擦系数为0.00166。基于辨识的模型参数，根据经验整定法，经仿真实验选取PID控制器参数=15，=0.3，=30。

在如图3所示的实验装置上进行柔性连杆振动抑制实验验证。图13描述的是系统规划的位移曲线。图14描述的是在跟踪类方波加速度规划的位移情况下，左边为无补偿作用下加速度响应的时域曲线，右边为广义最小方差补偿作用下加速度响应的时域曲线。由图14的时域对比图，经过均方根值计算得到图15。图15描述的是系统在广义最小方差补偿作用和无补偿作用下加速度响应的均方根值对比。如图15所示，系统有无补偿作用下，在起始0 和停止阶段2.4 后振动幅度的均方根值都在0.3 之内。但是运行过程中，补偿作用下，顶端加速度的振动幅值会剧烈变化，特别在加速变为减速0.6 ，1.8 过程中，以及1.2 换向运动过程中，振动幅值的均方根值会在0.6 内波动;而系统在广义最小方差补偿作用下，根据公式（11）实时估计出振动加速度信号，采用最小方差控制实时补偿柔性力矩，在加减速和换向0.6 ，1.2 ，1.8 时，振动幅值的均方根值减小到0.3 之内。除0.6 ，1.2 ，1.8 这几个特殊的时间点，在加减速过程中，无补偿作用下柔性连杆的振动幅值的均方根值在0.8 之内波动;在广义最小方差补偿作用下，柔性连杆的振动幅值的均方根值在0.4 之内波动。图15加速度响应均方根值对比证明在跟踪输入整形规划的位移信号下，广义最小方差抑制振动方法的有效性。

4 总 结

针对单自由度滚珠丝杆驱动柔性连杆运动过程产生振动问题，研究一种基于加速度整形、柔性力矩估计与前馈补偿的振动抑制方法。在搭建的滚珠丝杆滑块驱动柔性连杆的实验平台上进行实验验证。实验结果表明所研究方法的有效性。然而系统柔性模型包含1个弹性振动模态，研究的柔性连杆振动控制方法适合低阶振动模态的抑制，对于中高阶振动模态的抑制方法，理论上可行，需进一步做实验验证。

参考文献：

[1] Singhose W. Command shaping for flexible systems： A review of the first 50 years[J]. International Journal of Precision Engineering and Manufacturing， 2009， 10（4）： 53-168.

[2] Mohamed Z， Tokhi M O. Command shaping techniques for vibration control of a flexible robot manipulator[J]. Mechatronics， 2004， 14（1）： 9-90.

[3] 李 琳， 胡锡钦， 邹焱飚. 模态参数识别和输入整形相结合的抑振方法[J]. 振动、测试与诊断， 2019， 39（3）： 565-570.

LI Lin， HU Xiqin， ZOU Yanbiao. Residual vibration suppression by an integrated method of parameter identification and input shaping[J]. Journal of Vibration， Measurement & Diagnosis， 2019， 39（3）： 565-570.

[4] Zhao Y， Chen W， Tang T， et al. Zero time delay input shaping for smooth settling of industrial robots[C]. 2016 IEEE International Conference on Automation Science and Engineering， TX， USA， 2016： 620-625.

[5] Stanislao G， Gironimo G D， Singhose W， et al. Input predictive shaping for vibration control of flexible systems[C]. 2017 IEEE Conference on Control Technology and Applications， Hawaii， USA， 2017： 305-310.

[6] Biagiotti L， Melchiorri C， Moriello L. Optimal trajectories for vibration reduction based on exponential filters[J]. IEEE Transactions on Control Systems Technology， 2015， 24（2）： 609-622.

[7] 陈特欢， 杨依领， 吴高华， 等. 柔顺宏微操作器的最优抑振轨迹规划研究[J].振动工程学报， 2018， 31（4）： 611-619.

CHEN Te-huan， YANG Yi-ling， WU Gao-hua， et al. The optimal trajectory planning of a flexure-based macro-micro manipulator for its vibration suppression[J]. Journal of Vibration Engineering， 2018， 31（4）： 611-619.

[8] Kim J， Croft E A. Preshaping input trajectories of industrial robots for vibration suppression[J]. Robotics and Computer-Integrated Manufacturing， 2018， 54（6）： 35-44.

[9] Li J， Deng H. Vibration suppression of rotating long flexible mechanical arms based on harmonic input signals[J]. Journal of Sound and Vibration， 2018， 436（49）： 253-261.

[10] Meckl P H， Kinceler R. Robust motion control of flexible systems using feedforward forcing functions[J]. IEEE Transactions on Control Systems Technology， 1994， 2（3）： 245-254.

[11] Meckl P H， Seering W P. Minimizing residual vibration for point-to-point motion[J]. Journal of Vibration Acoustics Stress and Reliability in Design， 1985， 107（4）： 378-382.

[12] Meckl P H， Seering W P. Experimental evaluation of shaped inputs to reduce vibration for a cartesian robot[J]. Journal of Dynamic Systems， Measurement， and Control， 1990， 112（2）： 159-165.

[13] Qiu Z C， Li C， Zhang X M. Experimental study on active vibration control for a kind of two-link flexible manipulator[J]. Mechanical Systems and Signal Processing， 2019， 118（2）： 623-644.

[14] Qiu Z C. Adaptive nonlinear vibration control of a Cartesian flexible manipulator driven by a ball screw mechanism[J]. Mechanical Systems and Signal Processing， 2012， 30（4）： 248-266.

[15] Qiu Z C， Wu H X， Ye C D. Acceleration sensors based modal identification and active vibration control of flexible smart cantilever plate[J]. Aerospace Science and Technology， 2009， 13（6）： 277-290.

[16] 馬驰骋， 张希农， 代祥俊， 等. 含变质量构件的轴向运动梁的横向振动主动控制[J]. 振动工程学报， 2019， 32（3）： 396-403.

Ma Chicheng， Zhang Xinong， Dai Xiangjun， et al. Transverse vibration control of an axially moving beam system with time varying mass[J]. Journal of Vibration Engineering， 2019， 32（3）： 396-403.

[17] Erkorkmaz K. High speed CNC system design. Part II： Modeling and identification of feed drives[J]. International Journal of Machine Tools & Manufacture， 2001， 41（10）： 1487-1509.

[18] Ngo H Q T， Nguyen Q C， Kim W H. Implementation of input shaping control to reduce residual vibration in industrial network motion system[C]. 2015 15th International Conference on Control， Automation and Systems， Busan， Korea， 2015： 1693-1698.

[19] Kapsalas C N， Sakellariou J S， Koustoumpardis P N， et al. An ARX-based method for the vibration control of flexible beams manipulated by industrial robots[J]. Robotics and Computer-Integrated Manufacturing， 2018， 52（4）： 76-91.

[20] Peza-Solís J F， Silva-Navarro G， Castro-Linares R. Control of a rigid-flexible two-link robot using passivity-based and strain-feedback approaches[C]. 2010 7th International Conference on Electrical Engineering Computing Science and Automatic Control （CCE） Chiapas， México， 2010： 476-481.

作者簡介： 徐建明（1970-），男，博士，教授。电话：13967182316; E-mail： xujm@zjut.edu.cn