基于时变内力加权指标的大型冷却塔等效静风荷载
2021-12-16赵林陈旭展艳艳葛耀君
赵林 陈旭 展艳艳 葛耀君

摘要: 等效静风荷载是对动态风荷载和结构惯性力的拟静力化等价荷载模式,涵盖结构预期动力响应包络值,属结构设计中的荷载效应简化分析环节。在大跨空间结构抗风设计中,等效准则选取与荷载模式识别是将复杂动力问题转化为拟静力问题的关键步骤。目前等效静风荷载的评价准则众多,不同准则下的等效模式差异明显,缺少统一的共识性标准。为了体现不同风致内力响应对结构安全的综合影响,将评价准则由单一的荷载或内力层面拓展到多种内力加权组合层面。对于钢筋混凝土空间结构,该准则以物理概念清晰的配筋率作为表现形式,并融入结构动力响应时变特征。以某大型冷却塔为例,在脉动风压加载条件下进行时域分析得到风致结构动力响应时程,根据时变内力加权组合计算结构动态配筋率;从单一内力和内力加权两个层面评价现行规范等效静风荷载的抗风安全冗余度;以配筋包络线为等效目标,反演获得了兼顾多种内力加权组合的等效靜风荷载分布模式,阐明了相关算法和等效策略的合理性和工程适用性。
关键词: 大跨空间结构; 风荷载; 大型冷却塔; 时变内力加权组合; 动态配筋包络
中图分类号: TU393.3; TU312+.1 文献标志码: A 文章编号: 1004-4523(2021)05-0922-12
DOI:10.16385/j.cnki.issn.1004-4523.2021.05.005
1 背 景
风荷载为引起结构动力响应的随机动态荷载。结构风致响应分析时常把风荷载人为地划分为平均分量和脉动分量,并分别考虑其对结构的作用。针对冷却塔这类高耸薄壁空间结构,国内外学者通过现场实测[1?2]和风洞试验[3?4]研究了表面平均风压和脉动风压分布规律及其对结构响应的影响[5?6]。实际工程应用中为简化分析计算过程[7],引入了等效静风荷载概念,即在平均风压的基础上进行放大或修正以考虑荷载脉动引起的风振效应,从而将动力问题转化为静力问题。该策略也是世界各国制定以冷却塔为代表的大跨空间结构风荷载规范条款的重要依据[8?9]。
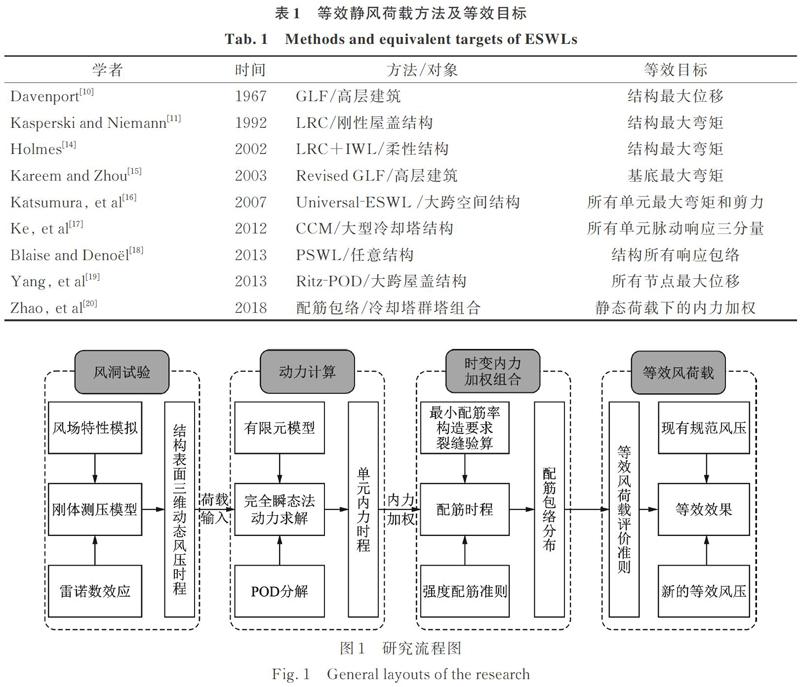
等效静风荷载理论研究中最具代表性的为Davenport[10]于1967年提出的GLF(Gust Loading Factor)方法以及Kasperski等[11]于1992年提出的LRC(Load Response Correlation)方法。其中,基于GLF法的等效静风荷载被编入包括中国在内的许多国家的建筑结构设计规范[12],LRC法亦被澳大利亚等一些国家的规范所采用[13]。后续学者在此基础上不断改进,针对不同结构类型提出了风荷载作用下与等效目标匹配的等效静风荷载模型(详见表1)[10?11,14?20]。上述等效静风荷载模型的等效目标众多,如薄膜力、位移、弯矩等,当结构存在多个控制目标时难以同时考虑或满足。为解决此类多目标等效问题,Katsumura等[16]首次提出了全局等效风荷载理论,等效静风荷载模型逐渐从仅关注特定部位极值响应的单目标等效向包络所有单元结构效应极值的多目标等效的趋势发展。
等效静风荷载分布模式与等效目标评价准则息息相关,不同评价准则各有适用性且难于同时兼顾,具体表现为:同一结构不同构件的控制内力不同,相同构件不同加载条件下的控制内力也不同,难以评价不同准则的优劣;结构的整体强度、刚度和稳定性由不同响应共同决定,以单一结构响应为目标建立的等效静风荷载分布模式难以兼顾整体最不利情况;而多目标全局等效静风理论更多地体现为数学意义上的统一拟合优化策略,无法明确气动力等效分布模式的物理意义。针对上述问题,本文提出基于时变内力加权组合的等效静风荷载评价准则;与以往单一的评价准则相比,该准则是风荷载作用下结构所有内力指标的汇总和深化,能考虑不同内力对结构安全的综合贡献,而不拘泥于追求对某一特定响应的等效。实际工程应用中钢筋混凝土结构的内力加权组合可体现为配筋量,钢结构的内力加权组合可体现为构件截面尺寸,这种对应关系为该评价准则的实际应用奠定了基础。Zhao等[20?22]已结合此概念进行了群塔干扰条件仅考虑冷却塔平均风压作用下静态内力加权的等效风荷载研究,初步证明了其有效性和可行性。本文将在此基础上,进行动态风压作用下的动力效应分析,探究动力响应条件下的风荷载等效模式。与前人研究的主要区别为:不再将动态风压拆分为平均部分和脉动部分,即不再根据平均风压和风振系数计算风致响应;而是将动态风压作用下结构效应时域分析的概念进一步推广到结构配筋响应层面。该过程综合了静、动态荷载分布模式和结构效应综合贡献,避免了现有规范中基于特定效应的风振系数简化近似处理方式,物理概念更加明确。
在上述思路的指导下,以某大型冷却塔为实例,确定如下研究方案(如图1所示):实施刚体模型测压风洞试验,获得塔筒内、外表面动态风压时程;加载脉动风荷载,进行结构动力响应有限元分析,获得结构内力响应时程;根据时变内力加权组合进行结构强度设计,得到动态配筋时程和配筋包络曲线;从单一内力和不同内力加权组合等多个角度,评价现行规范二维风压分布模式的抗风安全冗余度及不同评价指标的适用性;以配筋包络曲线为等效目标,根据风洞试验风压系数均值和标准差,提出新的等效静风荷载分布模式,并验证其有效性。
2 概念说明
2.1 内力加权组合与结构配筋
内力加权组合反映了不同内力对结构安全的综合影响,由于不同类别的内力具有不同的物理意义和单位,很难通过数值大小直接评价其在结构安全中的地位,也不能简单通过数值加权组合体现之间的共同作用。钢筋混凝土结构中的配筋设计为实现内力的合理加权组合及确定物理意义清晰的量化指标提供了参考依据,内力加权组合系数并非取自经验参数组合,而是借助半理论半经验的结构配筋计算实现;量化指标不是直接加权组合后的数值大小,而是构件的配筋量。通过这种方式,将不同单位、不同物理意义的内力转换成能够直接量化比较的配筋率。
根据《混凝土结构设计规范》GB 50010?2010[23],结构构件的配筋面积由材料特性()、单元尺寸()和内力大小()共同决定。对于钢筋混凝土超大型冷却塔,风荷载是塔筒结构设计的控制荷载,塔筒配筋设计分别在环向和子午向的内、外表面进行,共有四类配筋(如图2所示),即子午向外侧钢筋(MO)、子午向内侧钢筋(MI)、环向外侧钢筋(CO)和环向内侧钢筋(CI)。动态风压作用下,内力随时间变化,对应地可以得到随时间变化的配筋结果
上述塔筒壳体单元从内力到配筋过程可按照《混凝土结构设计规范》GB 50010?2010[23]中的偏心受力构件配筋,求解配筋率的主要公式如下:
式中 为符合大偏心受压单元的轴力,为符合小偏心受压单元的轴力,为单元所受弯矩,为选用混凝土的抗压强度,为截面宽度,计算中长度取1 m,与分别为受拉与受压钢筋的强度设计值,则为考虑钢筋没有到达强度设计值时的应力,为截面受压区有效高度,根据不同位置处壁厚换算得到,为钢材的弹性模量,为钢材的极限应变,为相对受压区高度,为单元外侧的配筋量,为单元内侧的配筋量,将计算所得每延米范围内的配筋面积定义为单元配筋量,单元配筋量按不同方向内外侧共有四种类型,即环向外侧、环向内侧、子午向外侧、子午向内侧。
由于风向的不确定性以及冷却塔塔筒结构的旋转对称特性,实际设计时同一高度处仅取一组配筋结果用于所有环向构件,形成沿塔筒高度方向变化的四类配筋包络线。该设计过程涵盖塔筒单元配筋动态时程的两次包络环节:
第一次是时间配筋包络,即针对计算时间段内的每个塔筒单元分别取具有一定概率保证率的配筋极值,获得空间三维时间配筋包络面,该极值可以简化为均值+峰值因子×均方根,高斯过程下当峰值因子取3.5,可获得具有99.5%概率保证率的极值[24],如下式
式中 为单元的配筋包络值,为单元配筋量在时程上的均值,为单元配筋量在时程上均方差,为时程参数,为环向角度参数,为高度项参数,为峰值因子,取3.5。
第二次为空间配筋包络,即针对时间配筋包络面在塔筒同一高度取最大值,得到沿高度变化空间配筋包络线,如下式
式中 为将各风向角下结果沿环向取极值的过程函数,本文以单塔为例,考虑结构和荷载的对称性,仅需单一风向角。
下文内力和配筋包络线均建立在此方法基础上。
2.2 规范风压分布
冷却塔结构设计规范《火力发电厂水工设计规范》(DL/T5339?2018[25],后文简称《水工规范》)中采用“静态风压×风振系数”考虑风对结构的作用,对应的塔筒外表面等效静风荷载定义如下
式中 为作用在塔筒外表面等效风荷载标准值;为风振系数,B类地貌取1.9;为群塔干扰系数,单塔取1;为风压高度变化系数;为基本风压;为子午向高度;为环向角度;为平均风压体型系数,外表面平均风压分布如下式所示
式中 为项数,无肋双曲冷却塔取7;为系数,无肋塔?取值分别为-0.4426,0.2451,0.6752,0.5356,0.0615,-0.1384,0.0014,0.0650。
塔筒内表面风压沿环向和子午向均匀分布,等效静风荷载定义如下:
式中 为内吸力标准值;为内吸力系数,取-0.5;为塔顶风压设计值;为塔顶标高处风压高度变化系数;与外压相同,为基本风压。
下文研究的单塔等效静风荷载采用无量纲风压形式,对应式(8)与(10)中考虑风振效应的内、外表面风压体型系数的合量。
3 风洞试验及有限元分析
3.1 风洞试验
原型冷却塔结构高185 m,塔顶直径82.5 m,喉部高度156.8 m,喉部直径79.2 m,通风口离地高度27.5 m,塔筒底部直径126.8 m,通风筒壳体沿高度指数变厚,喉部最小壁厚0.25 m,下环梁最大壁厚1.75 m,塔筒由48对直径为1.8m的X型柱支撑,塔筒直径和壁厚沿高度分布如图3所示。
综合考虑结构尺寸、风洞试验段大小、阻塞率和雷诺数效应模拟等因素,冷却塔刚性测压模型几何缩尺比为1∶300,对应的风洞阻塞率为0.7%<5%。模型内、外表面沿高度方向分别布置4层和12层测压点,每层均匀布置36个测点,共计布置12×36=432个外压测点,4×36=144个内压测点(如图4所示)。冷却塔这类圆截面结构表面绕流特性对雷诺数效应非常敏感,本文通过控制风速和改变模型表面粗糙度相结合的方法实现亚临界雷诺数下模拟高超临界钝体绕流特征[26]。其中,通过在塔筒外壁粘贴不同层数的粗糙纸带来调节模型表面粗糙度,每层粗糙纸带宽10 mm,厚0.1 mm。雷诺数模拟标准为《水工规范》[25]建议的原型冷却塔外表面平均风压实测曲线和Zhao[2]等基于大型冷却塔实测的脉动风压分布曲线。当冷却塔外表面粘贴4层纸带时,雷诺数效应模拟效果最好,补偿后的塔筒外压系数均值和脉动值分布如图5所示。
刚体模型测压风洞试验在同济大学土木工程防灾国家重点实验室TJ?3大气边界层风洞中进行,该风洞为闭口回流式矩形截面风洞,试验段宽15 m、高2 m、长14 m,风速调节范围为0?17.6 m/s。试验中利用尖劈和粗糙元模拟B类地貌风场,风速比为1∶5,模拟的平均风剖面、紊流度和顺风向风谱与规范吻合良好[12](如图6所示)。
3.2 有限元分析
冷却塔建模时塔筒离散为空间壳Shell63单元,X型支柱和环基采用空间梁Beam188单元[27],支柱底与环基刚性连接。塔筒沿高度划分为55层,从塔底到塔顶依次编号L1?L55,第53和54層分别为塔顶刚性环的裙板和竖板,每层沿环向均匀划分96个单元,支柱划分为96个单元,环基划分为144个单元;塔筒和支柱采用C40混凝土,环基采用C30混凝土;建模效果和结构动力特性如图7和表2所示。
为了研究风荷载作用下的结构响应,加载的风荷载分别来源于风洞试验的动态风压时程和《水工规范》 [25]定义的B类地貌下无肋双曲等效静风荷载(见式(2)?(5)),设计基本风速均取50 m/s。动态风压时域分析中,使用本征正交分解法(POD法)[28]将塔筒内、外表面风压测点拓展至与有限元模型对应的56×96个节点。图8以塔筒中部第20层单元(L20)迎风驻点的子午向轴力和子午向外侧配筋为例,展示结构内力时程、配筋时程和对应的概率包络值,其中的配筋率最小值由规范[23]最小配筋率控制。
4 等效准则
4.1 单一风致内力准则
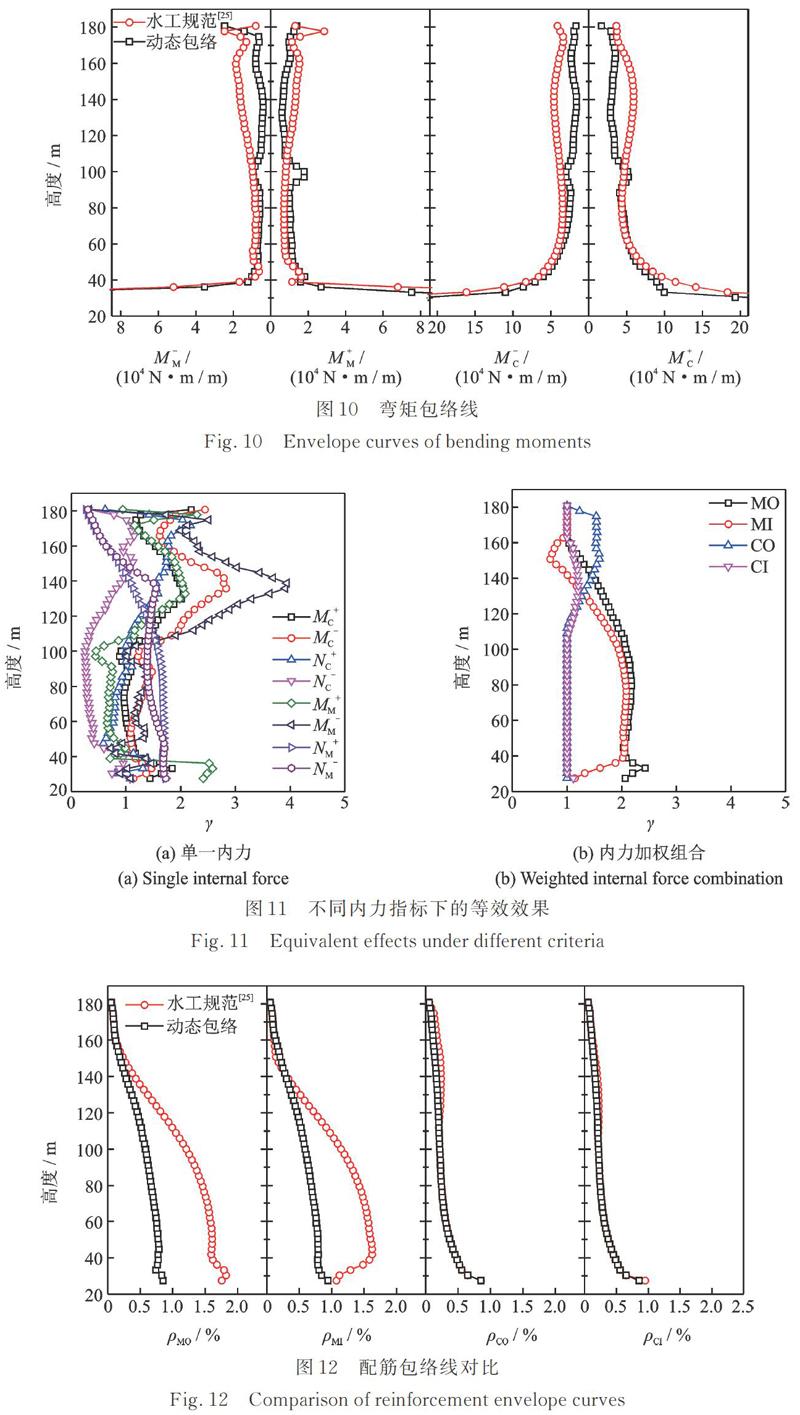
风致内力是目前等效静风荷载等效效果评价的主要依据,分别选取子午向轴力、环向轴力、子午向弯矩和环向弯矩的包络曲线对比规范风压[25]和动态风压对不同内力的等效效果(如图9?10所示);其中,规范风压下的内力包络线取同一高度环向所有单元内力分析的极值,动态风压下的内力包络线则根据3.1节的方法确定。为量化两者差异,定义等效比例系数如下
式中 为等效比例系数,即规范风压和试验动态风压下的响应包络的比值。和分别为规范风压和试验动态风压下响应包络值。
由于动态包络值源于脉动风荷载动力配筋计算,规避了风振系数这类简化处理,更接近真实情况,因此作为比较的参照标准;说明规范等效静风荷载存在一定的冗余度;说明规范等效静风荷载不能保证结构的安全;说明等效效果较好,同时兼顾结构经济性和安全性。
图9和10分别给出了两种风压模式下轴力和弯矩响应包络随塔筒高度的变化。对于风荷载作用下的主要控制内力——子午向轴力:塔筒喉部以下,规范风压在塔筒中下部可以完全涵盖动态风压包络值,并存在一定冗余,最大值冗余度为70%;塔筒喉部以上,规范值不能完全包络动力分析结果,但二者差异较小。对于数值较小的环向轴力:环向压力在喉部以下,规范值小于动力包络值,在喉部以上规范值与动力包络值差异较小;环向拉力在喉部以下,两类风压模式下的结果较为接近,在喉部以上规范值有冗余。对于子午向和环向弯矩和,两类风压模式下的计算结果在塔筒中下部差异较小,在喉部附近规范值具有较高的冗余度。由单一内力的等效比例系数可见(如图11(a)所示):不同种类内力之间,甚至是同种类别不同方向的内力之间,比例系数没有确定的分布规律,这反映出冷却塔结构风致响应的复杂性,以不同类型内力为标准建立的等效静风荷载模式将存在较大差异;内力层面相对无序的分布规律也证明了寻找同时满足所有内力等效的多目标等效风荷载分布模式是极其困难的。图11(b)给出的基于内力加权组合的等效比例系数分布规律简洁明了,这为下一步的等效荷载分布模式研究提供了便利,尤其在喉部区域附近,四个指标的差异显著,应重点关注。
4.2 内力加权组合准则
图12对比了基于试验风荷载动力分析获得的时变加权内力的配筋包络值与规范等效静风荷载作用下的塔筒配筋值,可以看出:对于环向内、外侧配筋和,两种风压分布模式下的结果非常接近,差别主要体现在喉部附近,这是由于冷却塔沿环向配筋量较少,多数情况下由最小配筋率控制,风荷载模式差异不会引起配筋量的显著变化。两种风压模式结果的差异主要表现在子午向配筋和,规范值在塔筒中下部大于动态包络值,存在过高的安全储备,最大冗余度可超过50%;但在喉部附近,规范风荷载作用下的子午向内侧配筋数量不足,存在安全风险隐患。
5 等效静风荷载
5.1 改进算法理论
由上节可知,无论是以单一内力作为等效目标,还是以内力加权组合作为等效准则,目前水工规范[25]中等效静风荷载整体安全储备过高,但在塔筒喉部等局部薄弱位置又存在安全隐患,有必要提出新的等效静风荷载分布模式来兼顾结构安全性和经济性。由于以单一风致内力为目标的等效效果差异显著,导致基于不同种类内力作为等效准则的风荷载分布模式可能存在较大差异;而基于内力加权组合的配筋包络作为等效模式物理意义明确,分布规律简洁明了、趋势性强,故将其作为本节的等效目标。
风荷载作用下结构动力响应极值可以表示如下
式中 为设计动力响应极值,为响应空间线性无关的一组基向量,为组合系数向量,为由组成的矩阵,也称为标准响应,可表示为如下形式
式中 即为作用在结构上的等效静风荷载向量,该向量是荷载矩阵中每一列荷载向量的线性组合。
本文等效静风荷载模式的反演以风洞试验的动态风压为基础,將荷载的平均值和标准差作为荷载矩阵的基向量进行线性组合,整个过程包含等效风压系数基线确定以及塔筒高度调整系数选取两个环节。
5.2 风压模式反演
(1)等效风压系数基线确定:对塔筒不同高度处风压系数平均值和标准差的极值和组成的曲线集合取上、下包络线Line1和Line2;分别在0°?90°及270°?360°的正压区(Zone1)选用Line1,在90°?270°负压区(Zone2)选用Line2;3段曲线相连,得到组合曲线。由于单塔风压分布的对称性,图13仅给出了0°?180°结果,180°?360°结果根据对称原则镜像;采用下式所示三角级数多项式对上述曲线组合进行拟合得到等效风压系数基线,拟合系数如表3所示。
(2)塔筒高度调整系数选取:由于塔筒不同高度安全冗余情况不同,沿塔筒高度取不同调整系数对等效风压系数基线进行放大或缩小
式中 为调整后的等效风压系数,为塔筒高度调整系数,为沿塔筒子午向高度。
本例中,塔筒上部1/3以上高度,调整系数取1.2,塔筒下部2/3以下高度取0.8。如下式所示
式中 为塔筒总高度。
沿高度方向调整后的等效风压分布曲线与规范风压相比具有以下特点:沿子午向分段变化,沿环向平缓变化;正压极值增大,负压极值减小,如图14所示。
5.3 等效效果对比
图15给出了本文提出的等效静风荷载、规范等效静风荷载和风洞试验动态风压作用下的子午向和环向内、外侧,,,四类配筋的包络值;并以动态包络作为精确解,对比了本文等效静风荷载和规范等效静风荷载的等效效果如图16所示。图16中,γMO,γMI,γCO和γCI分别表示子午向外侧、子午向内侧、环向外侧、环向内侧配筋包络的等效比例系数。可以看出:本文提出的等效风荷载分布模式能够显著降低塔筒子午向配筋量,尤其是塔筒中下部,显著改善了结构抗风安全冗余度;环向配筋在大多数塔筒位置仍由最小配筋率控制,风压分布模式的改变未对其造成明显的影响;但在喉部附近子午向配筋无法实现包络(图16中处于阴影区域的点),说明了塔筒喉部是冷却塔研究、设计和建造中重点关注的部位,必要条件下应需采取局部加强措施。
图17对比了3种风荷载分布模式下四类配筋用量和钢筋总用量。其中,本文提出的等效静风荷载所需钢筋总量与动态包络结果非常接近,但相比规范风压钢筋总用量减小约33%,显著提高了经济性。由于文中仅考虑了风荷载作用效应,并且只统计了上部塔筒结构,该值约为实际工程的1/3。
6 结 论
通过刚体模型测压风洞试验、結构有限元计算和动态配筋设计,分析了风荷载作用下的钢筋混凝土冷却塔单元内力和内力加权组合的分布规律;评价规范等效风荷载模式在单一内力层面和内力加权组合层面的等效效果和抗风安全冗余度;提出基于配筋包络指标的等效静风荷载分布模式,并对其等效效果进行验证。主要结论如下:
(1)同一等效静风荷载模式在不同内力指标下的等效评价效果差异显著,而基于时变内力加权指标的等效效果更具统一、简洁的分布规律;
(2)内力加权指标能够考虑不同内力对结构安全的综合影响且与实际工程应用紧密结合,推荐为等效风荷载的评价指标;
(3)从结构配筋的角度,现行水工规范的等效静风荷载存在较高的冗余度,主要表现在塔筒中下部,并在塔筒喉部位置附近存在安全储备不足的隐患;
(4)基于内力加权指标的等效风荷载分布模式以风洞试验风压系数均值和标准差为基础,能够较好地拟合塔筒配筋包络曲线,与规范风压模式相比,兼顾了抗风安全性和结构经济性。
本文以单塔工况为例梳理了相关概念和方法,群塔干扰工况时等效静风荷载分析流程不变,仅需根据干扰下的风压分布模式调整等效风压系数基线以及改变沿塔高的调整系数,后续将对复杂群塔组合工况开展更广泛的研究,验证提出的等效静风荷载模式的适用性。
参考文献:
[1] Pirner M. Wind pressure fluctuations on a cooling tower[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 10(3): 343-360.
[2] Zhao L, Ge Y J, Kareem A. Fluctuating wind pressure distribution around full-scale cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 165:34?45.
[3] 李鹏飞, 赵 林, 葛耀君,等. 超大型冷却塔风荷载特性风洞试验研究[J]. 工程力学, 2008, 25(6): 60-67.
Li P F, Zhao L, Ge Y J, et al. Wind tunnel investigation on wind load characteristics for super large cooling towers[J]. Engineering Mechanics, 2008, 25(6): 60-67.
[4] Armit J. Wind loading on cooling towers[J]. Journal of the Structural Division, 1980, 106(3): 623-641.
[5] Kasperski M, Niemann H J. On the correlation of dynamic wind loads and structural response of natural-draught cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 30(1-3): 67-75.
[6] Sollenberger N J, Billington D P, Scanlan R H. Wind loading and response of cooling towers[J]. Journal of the Structural Division, 1980, 106(3): 601-621.
[7] Davenport A G. How can we simplify and generalize wind loads?[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54(94): 657-669.
[8] VGB-R610ue. VGB-Guideline: Structural design of cooling tower-technical guideline for the structural design, computation and execution of cooling tower[S]. Essen: BTR Bautechnik bei Kühltürmen, 2005.
[9] BS4485. Code of practice for structural design and construction[S]. London: British Standard Institution, 1996.
[10] Davenport A G. Gust loading factors[J]. Journal of the Structural Division, 1967, 93(ST3): 11-34.
[11] Kasperski M, Niemann H J. The L.R.C. (load-response-correlation)?method a general method of estimating unfavourable wind load distributions for linear and non-linear structural behaviour[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1-3): 1753-1763.
[12] 中华人民共和国住房与城乡建设部.GB 50009-2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.
MOHURD. GB50009-2012, Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012.
[13] Australia Standard. Amendment 1 to AS/NZS 1170.2:2002 - Structural Design Actions - Part 2: Wind Actions[S], 2002.
[14] Holmes J D. Effective static load distributions in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(2): 91-109.
[15] Kareem A, Zhou Y. Gust loading factor—Past, present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(12): 1301-1328.
[16] Katsumura A, Tamura Y, Nakamura O. Universal wind load distribution simultaneously reproducing largest load effects in all subject members on large-span cantilevered roof[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9-11): 1145-1165.
[17] Ke S T, Ge Y J, Zhao L, et al. A new methodology for analysis of equivalent static wind loads on super-large cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 111: 30-39.
[18] Blaise N, Deno?l V. Principal static wind loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 113: 29-39.
[19] Yang Q, Chen B, Wu Y, et al. Wind-induced response and equivalent static wind load of long-span roof structures by combined Ritz-proper orthogonal decomposition method[J]. Journal of Structural Engineering, 2013, 139(6): 997-1008.
[20] Zhao L, Zhan Y Y, Ge Y J. Wind-induced equivalent static interference criteria and its effects on cooling towers with complex arrangements[J]. Engineering Structures, 2018, 172: 141-153.
[21] Yu M, Zhao L, Zhan Y Y, et al. Wind-resistant design and safety evaluation of cooling towers by reinforcement area criterion[J]. Engineering Structures, 2019, 193: 281-294.
[22] Zhao L, Chen X, Ge Y J. Investigations of adverse wind loads on a large cooling tower for the six-tower combination[J]. Applied Thermal Engineering, 2016, 105: 988-999.
[23] 中华人民共和国住房与城乡建设部. GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
MHOURD. GB50010-2010, Code for design of concrete structures[S]. Beijing: China Architecture & Building Press, 2010.
[24] 张相庭. 结构风压与风振计算[M]. 上海: 同济大学出版社, 1985.
Zhang X T. Structural Wind Pressure and Calculation of Wind-Induced Vibration[M]. Shanghai: Tongji University Press, 1985.
[25] 电力规划设计总院. DL/T 5339-2018, 火力發电厂水工设计规范[S]. 北京: 中国计划出版社, 2018.
China Electric Power Planning & Engineering Institute. DL/T 5339-2018, Code for hydraulic design of fossil fired power plant[S]. Beijing: China Planning Press, 2018.
[26] Kareem A, Cheng C M. Pressure and force fluctuations on isolated roughed cylinders of finite height in boundary layer flows[J]. Journal of Fluids and Structures, 1999, 13(7): 907-993.
[27] 王新敏, 李义强, 许宏伟. Ansys结构分析单元与应用[M]. 北京: 人民交通出版社, 2011.
Wang X M, Li Y Q, Xu H W. Ansys Structural Analysis Element and Application[M]. Beijing: China Communication Press, 2011.
[28] Tamura Y, Ueda H, Kikuchi H, et al. Proper orthogonal decomposition study of approach wind-building pressure correlation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72: 421-431.
作者简介: 赵 林(1974-),男, 教授,博士生导师。电话:(021)65984882;E-mail:zhaolin@tongji.edu.cn
通讯作者: 陈 旭(1988-),男,讲师。电话:(021)57125281;E-mail:chenxu@shnu.edu.cn
