干扰环境下基于计算机视觉的多目标动位移高精度监测方法

周洲 陈太聪

摘要： 当前基于计算机视觉的动位移测量研究通常要求高速高分辨率摄像机和理想拍摄环境，以保证测量的性能和精度。然而高速相机成本较高，目标成像需要较高对比度，且实际拍摄过程中环境条件也难以保持稳定，导致应用受限。结合时空上下文算法和光流算法，提出一种无需人工标靶点、鲁棒的多目标位移监测方法，通过智能手机实现干扰环境下的结构多点动位移同步测量。开展悬臂小球模型的扫频实验，检验方法在一定频率范围内的测量效果。其中，使用智能手机对激振小球进行拍摄，并在实验中保留复杂背景和模拟光照变化。分别采用所提方法和常用的特征光流算法对视频进行处理，得到动位移结果，并与位移传感器测量值进行对比。结果表明，在有光照变化干扰下，所提方法具有更强的抗干扰性，各监测点的最大位移偏差在5%以内。

关键词： 结构健康监测; 位移测量; 计算机视觉; 时空上下文; 光流

中图分类号： O327; TU317 文献标志码： A 文章编号： 1004-4523（2021）05-0979-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.011

引 言

在结构健康监测实践中，加速度传感器得到了广泛应用，可直接测量结构的加速度响应，但对于低频范围的应用效果不佳[1]。相反，位移传感器的低频测量结果更加精确，然而由于安装和测试的不便，应用相对较少，包括线性可变差动变压器需要固定支座辅助测量，而多普勒激光测振仪虽然可实现无接触测量，但测量结果受激光聚光影响较大，且设备成本也相对较高。

近年来，随着图像数据采集和计算机视觉技术发展，基于视觉的位移测量技术表现出无接触、远距离、低成本和高精度等优点，受到了广泛关注[2?3]。Dworakowski等[4]和韩建平等[5]利用图像模板匹配技术，使用高速相机实现了单点动位移测量，其中需要安装人工目标板辅助测量。另外，高速相机的目标成像需较高对比度，从而也要求高亮度的光照条件。周颖等[6]和Yoon等[7]分别根据特征点匹配算法和光流算法，在不附加任何人工标靶点的情况下，采用消费级相机获得结构的位移响应和动力特性。为减少特征误识别，方法对目标的纹理特征有一定的要求。Feng等[8]提出基于图像相关的亚像素模板匹配技术，改善了目标动态位移的提取精度。值得说明的是，上述研究都是在理想的测量条件下进行的，需要稳定的光照环境，未考虑光照环境干扰对测量结果的影响。基于此，Dong等[9]应用时空上下文算法，实现了光照变化和雾气环境下的位移监测。但研究仅限于单点动态位移测量，未实现多点同步监测，此外所采用的专业摄像机，成本较高。

针对上述若干问题，本文提出应用智能手机同步监测光照环境变化情况下多目标动位移的技术方法。其中，结构振动视频由智能手机采集，且监测目标点的数目不受限，多个监测目标点由多个预定义的可重叠区域自动集合而成。继而，应用时空上下文（Spatio?Temporal Context，STC）算法和光流（Optical Flow，OF）算法，同步跟踪和获取所有目标监测点的高精度位移时程信息。最后，为了验证方法的可行性和可靠性，开展悬臂小球模型的扫频实验，使用智能手机对激振小球进行拍摄，通过实验模拟光照变化，对比考查本文方法与常用特征光流算法和位移传感器的测量结果。

1 多目标动位移监测流程

本文的研究重点集中在智能手机应用、多目标位移监测和高精度位移提取等三方面。其中，第一方面需要解决智能手机的相机广角畸变的校准问题;第二方面解决多目标选择和预定义问题;第三方面解决环境干扰下针对各目标的跟踪和高精度位移提取问题。

相应地，本文基于计算机视觉的结构振动位移测量流程如框图1所示。内容分为三大部分：相机标定、多目标定义、多目标跟踪和位移提取。本文方法所需测量设备为商业智能手机，无需其他传感器和设备。

以下分别对三大部分所用分析方法和具体操作展开详细论述。

2 智能手机的相机标定与图像校准

本文采用智能手机作为视频拍摄设备，安装其上的商业相机为了增大拍摄范围，大多选用的是广角镜头，但是该镜头会引入较大的径向和切向畸变。因此，为了减少畸变产生的位置误差，有必要对相机进行标定，识别相机的内外参数和畸变系数。基于标定后的畸变模型，校准所拍摄的图像，最终建立图像位移到结构位移的准确转换关系。

相机成像所基于的小孔成像模型，采用下式描述三维空间目标点与相机成像平面中的对应点 之间的关系[10]：

式中 ，和分别表示点在世界坐标系、相机坐标系和图像像素坐标系中对应坐标。为缩放因子;外部参数矩阵和分别表示旋转矩阵和平移矩阵，他们与相机物理位置有关;内部参数矩阵与相机构造和材料有关，表示为

式中 和分别为图像像素坐标系和轴上的比例因子;为坐标轴倾角参数;和为原点坐标。

式（1）和（2）代表理想成像关系，而实际上相机镜头会产生径、切向畸变，导致相机成像点发生偏移，可采用以下非线性畸变模型[11]进行描述

相机标定的基本原理，即是根據已知目标点的准确坐标（通常设计为）和相应成像点的畸变像素坐标（），结合式（1），（2）和（4），识别得到相机的内外参数矩阵、径向和切向畸变系数。通常采用最优化方法，反复迭代求解使得误差最小的内外参数和畸变参数。该误差定义为三维空间目标点计算的投影图像像素坐标与实际图像像素坐标之间的差值平方和。

具体操作时，本文采用张正友[10]方法进行相机标定，其中忽略影响，并使用黑白方块间隔组成的棋盘作为标定物，分别从不同角度、位置和姿态拍摄标定物，建立标定用照片库，最终通过不同数量照片的标定结果分析，获得智能手机iphone7后置摄像头的内部参数和畸变系数的收敛结果如表1和2所示。图2以前两阶径向畸变参数为例，示意了两者识别均值和标准差随所用照片数量的变化情况。由图表所示结果可见，相关相机的标定采用20张左右的照片可满足要求。

当相机完成标定获得相关参数后，即可结合式（2）和（4），先由实际照片上的畸变像素坐标（） 计算（），继而得到理想坐标（），最终得到校准后的照片上的理想像素坐标（）。如图3所示即为标定用黑白棋盘的某一张照片的局部在校准前后的图像对比。可见，原始图片中黑白方块的畸变扭曲边缘已较好地被修正为平直边缘。

3 多目标定义

在结构振动过程中，对多点动位移进行同步监测，不仅有益于全面了解结构振动形态，也有利于模态特征辨识等工作开展。

基于视频的多目标位移同步监测，要求能实现每个目标与其他目标的区分，并能跟踪各个目标在每帧照片中的位置。要达成这两个目标，一方面需要在首帧照片中预先定义监测目标对象;另一方面需要目标跟踪算法支持针对多目标对象的处理。

本文后续将采用时空上下文（STC）算法进行目标跟踪，然而传统STC目标跟踪算法只关注单个目标，无法同时跟踪多个目标[9， 12]。因此，本文对传统STC算法进行改进，通过并行化设计，及引入区域相容条件，实现了对多个可重叠目标区域的同步跟踪。

如图4所示为在结构振动视频的首帧照片中完成的多目标预定义。目标区域可根据典型结构区域自行定义，数量不限，且可部分重叠。每个目标区域（图中矩形框）的特征点为各区域的中心点（图中×形标记点），监测所得的各目标区域位移可由该区域中心点的位移进行代表。

4 基于STC算法的目标跟踪

4.1 STC算法基本模型

在利用计算机视觉技术进行目标跟踪时，目标对象与其局部场景之间存在密切关联，利用这种关系，更易于找到目标。STC算法[12]即基于贝叶斯框架，根据目标区域与其局部上下文的图像强度和位置之间的统计相关性进行建模计算。

该算法通过极大化以下置信度函数来追踪目标位置[12]

式中 为目标位置;为场景中的目标;为目标区域中心点位置;为归一化系数，以保证（）在0?1间变化;和分别为尺度参数和形状参数。

当前帧照片中，目标区域的局部上下文特征集定义为

式中 为位置处的图像强度;为目标点周围的局部上下文区域。如图5所示，黄色框代表跟踪目标，红色框代表其局部上下文。

依据贝叶斯概率公式，式（6）中的置信度函数可展开为

式中 为联合概率函数;为条件概率函数，表示目标位置与其局部上下文之间的空间关系;为上下文先验概率函数，表示局部上下文的外观特征。

首先，根据首帧照片的图像强度，以及预定义的目标位置，可计算上下文先验概率

式中 为归一化系数，以保证在0?1间变化;为尺度参数，和分别为目标区域的长度和宽度。

其次，定义条件概率函数为

式中 为空间上下文模型函数，取决于目标位置和局部上下文位置之间的相对距离和方向，且设置为非径向对称函數，该设置有助于解决距离和背景相似带来的歧义。

将式（9）和（12）代入式（8），可得

式中 代表卷积运算符。

每一帧图片中的像素点数量众多，式（13）的卷积运算效率低且计算复杂。已知在时域中进行卷积运算的结果与其在频域的乘积运算结果一致，因此，为了提高计算效率，STC算法结合快速傅里叶算法（FFT），将卷积运算转换成乘积运算，可大幅提高运算效率。由此，式（13）经FFT转化为

式中 表示傅里叶变换，表示对应位置的乘积。

对式（14）进行傅里叶逆变换，并将式（6）代入，最终可得空间上下文模型函数的求解列式为

式中 表示傅里叶逆变换（IFFT）。

4.2 STC算法跟踪过程

STC算法将目标跟踪任务转换为对置信度函数）的最大值搜索任务，其流程如图6所示。在第t帧照片中，通过式（15）计算得当前帧照片的空间上下文模型，继而根据下式更新下一帧照片的时空上下文模型

式中 为学习速率因子;定义为前一帧照片的时空上下文模型和空间上下文模型的加权和。这种加权处理可以有效地抑制物体外观强度突变引起的噪声干扰。

在获得后，由式（14），第t+1帧的置信度函数相应更新为

最后，通过搜索置信度函数的最大值，从而确定第t+1帧照片中的目标位置为

这里需要说明的是，由于本文仅以结构平面内振动为例进行论述，因此忽略了纵向测试距离上的尺度变化，即图片大小比例未发生变化;如果要观测结构三维振动，即存在平面外运动，结构与相机间的纵向测试距离会发生明显的变化，则还需引入目标尺度更新模型[12]进行修正。

为了达到稳健的跟踪效果，在STC跟踪算法中的若干关键计算参数，按照参考文献[12]的建议，取：=2.25，=1，=0.075，=1。

5 基于OF算法的亚像素位移估计

根据以上STC算法得到的图片目标位置的分辨率为单个像素，此时目标实际位移的测量精度为单个像素所对应的实际位移。因此，为了获得更精确的目标实际位移，除了提高相机的分辨率以加密图片中的像素点之外，还可以采用光流（OF）算法，对图片目标在单个像素内的位置变化进行估计，以提取亚像素位移[13]。

一般地，视频中相邻两张照片的图像强度和之间满足以下关系

在利用STC跟踪算法获得整像素位移（）后，参照该位移，在目标图像中截取新的模板图像。新的模板图像和目标图像之间仍存在微小位移（），此时应用光流算法，可建立新的模板图像和目标图像之间的近似关系

式中 偏导数可采用有限差分计算，即及。

如图7所示为视频中相邻图像的亚像素位移估计的计算流程。相关研究表明[13]，根据光流算法优化得到的亚像素位移精度可达到0.0125像素，可以有效地识别目标在单个像素内的位置变化，有利于提升实际目标位移的测量精度。

6 模型实验

本文将开展悬臂小球模型的强迫振动实验，以检验所提出的方法在无人工标记点和有光照变化环境下，能否利用商业相机准确地获取结构的多点动位移时程。实验将以位移传感器测量结果为基准，对比本文方法与常用特征光流算法[7]的效果。

6.1 实验设计

实验装置如图8所示，小钢球通过竖直连杆固定在底部支座上，激振器与竖直连杆相连。小钢球上连接有直线位移传感器，传感器另一端支撑在左端立柱上。实验中，激振器输入外部激励引起小球水平振动，位移传感器记录小球的水平位移时程，并由数据采集卡和电脑进行自动采集。同时，由放置在小球前端、安装在三角架上的iphone7手机录制小球振动视频，设置图片分辨率为1920×1080像素，帧率为60幀/s。实验测量的小球振动时长为20 s。

实验中，为了检验结构常见振动频率范围内的方法可行性，设置激振器激励为1?10 Hz间的重复线性扫频。此外，为了考查方法在真实背景环境下的应用效果，没有对小球背后的复杂背景进行遮挡。

为了考查方法在光照变化环境下的应用效果，特设计两组对比实验：（1）情况一，在小球振动过程中，光照条件不变化;（2）情况二，在小球振动过程中，3次调节临近的台灯光照亮度。实验用台灯有3档亮度可调，如图9（a）所示为关闭台灯时的照片，如图9（b）所示为打开台灯最亮档时的照片，由图可见两者差别明显。

6.2 实验结果

为了便于与位移传感器的测量结果进行直接对比，选择图4中与位移传感器同一高度的两个目标作为跟踪目标。如图10所示为初始设置的两个跟踪目标，红色框为目标区域1，绿色框为目标区域2，蓝色点为各目标区域的中心。

根据本文提出的技术方案，首先将拍摄视频中的每一帧照片进行校准;继而计算每一帧照片中目标区域的置信度函数，通过STC算法和OF算法对相邻帧进行匹配，得到目标的图像位移;最后将图像位移乘以缩放影响矩阵得到最终位移。

作为对比分析用的常用特征光流算法，则是采用Lucas?Kanade光流与Harris角点相结合的算法，通过计算相邻两帧的关键特征点的光流，获取关键点的位移[7]。

为了比较本文算法与特征光流算法的性能，现定义如下两类评价指标[14]，归一化均方误差指标NMSE和相关系数指标：

式中 和分别代表基于视觉算法和位移传感器获得的位移数据;和分别代表不同方法得到的数据均值。两个指标的取值范围都在0?1之间，指标值越大，意味着越相关，数据相似程度越高。

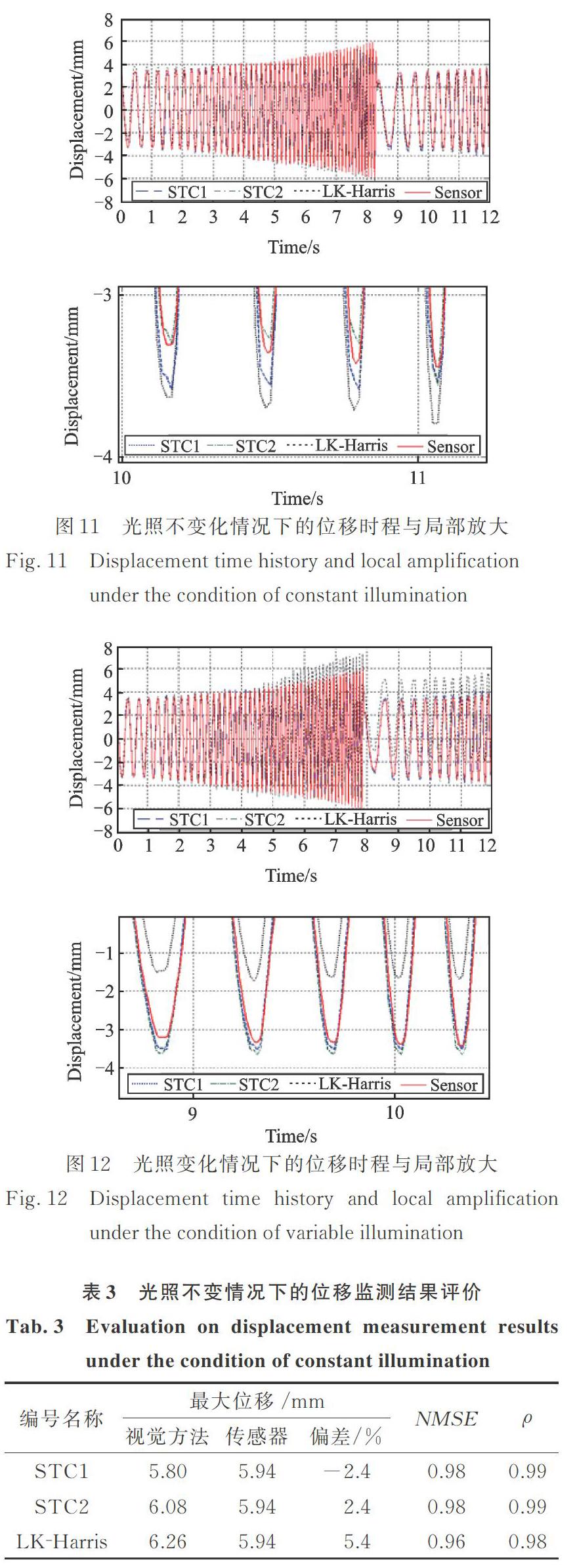
如图11和12所示分别为光照不变化情况和光照变化情况下的12 s位移时程对比图，其中STC1和STC2代表应用本文方法识别得到的目标1和目标2结果，LK?Harris代表特征光流法识别结果，Sensor代表位移传感器测量结果。如表3和4所示为两种情况下的不同方法评价指标结果，表中还列出了最大位移对比结果。

由图表所示结果可见：

（1）在光照不变化情况下，本文方法和特征光流法所得的位移时程与位移传感器的测量结果在形状和趋势上可保持一致，表明两种方法都有良好的适应复杂背景的能力，总体上本文方法结果更接近实测位移结果。表列数据也显示了同样结论，NMSE和都接近于1，最大位移偏差都小于6%，而本文方法的指标值更为优越。需要说明的是，STC1和STC2的结果不完全一致，除了视频识别误差外，振动过程中的支撑杆弯曲变形，导致两个目标点的水平位移也会存在轻微的客观差异。

（2）在光照变化情况下，特征光流法的位移时程发生了明显的偏移，表明目标跟踪失败，而本文方法所得的位移时程仍可与位移传感器的测量结果在形状和趋势上保持一致。表列数据也显示了同样结论，特征光流算法的NMSE和明显偏小，最大位移误差大于15%;而本文方法的指标值虽然较光照不变化的理想情况略有降低，但NMSE和仍能保持在0.95左右，最大位移偏差小于5%，表明本文方法具有良好的抗光照变化能力。

7 结束语

本文针对计算机视觉技术在结构工程振动领域的应用开展研究，基于时空上下文算法和光流算法，提出了应用智能手机实现环境变化情况下多目标动位移同步监测的技术方法。实验表明，本文方法具有良好的复杂背景适应能力和抵抗光照变化能力，显示了较强的工程应用潜力。未来的实际应用还有必要进一步研究更为复杂的环境变化情况，如遮挡、雾天和相机抖动等的不利影响。

参考文献：

[1] Cho S， Spencer Jr B F. Sensor attitude correction of wireless sensor network for acceleration‐based monitoring of civil structures [J]. Computer‐Aided Civil and Infrastructure Engineering， 2015， 30（11）： 859-871.

[2] Spencer Jr B F， Hoskere V， Narazaki Y. Advances in computer vision-based civil infrastructure inspection and monitoring [J]. Engineering， 2019， 5（2）： 199-248.

[3] Feng D， Feng M Q. Computer vision for SHM of civil infrastructure： From dynamic response measurement to damage detection—A review[J]. Engineering Structures， 2018， 156： 105-117.

[4] Dworakowski Z， Kohut P， Gallina A， et al. Vision-based algorithms for damage detection and localization in structural health monitoring[J]. Structural Control and Health Monitoring， 2016， 23（1）： 35-50.

[5] 韩建平， 张一恒， 张鸿宇. 基于计算机视觉的振动台试验结构模型位移测量[J]. 地震工程与工程振动， 2019， 39（4）： 22-29.

HAN Jian-ping， ZHANG Yi-heng， ZHANG Hong-yu. Displacement measurement of shaking table test structuremodel based on computer vision [J]. Earthquake Engineering and Engineering Dynamics， 2019， 39（4）： 22-29.

[6] 周 颖， 张立迅， 刘 彤， 等. 基于计算机视觉的结构系统识识[J]. 土木工程学报， 2018， 51（11）： 17-23.

ZHOU Ying， ZHANG Li-Xun， LIU Tong， et al. Structural system identification based on computer vision [J]. China Civil Engineering Journal， 2018， 51（11）： 17-23.

[7] Yoon H， Elanwar H， Choi H， et al. Target‐free approach for vision‐based structural system identification using consumer‐grade cameras [J]. Structural Control and Health Monitoring， 2016， 23（12）： 1405-1416.

[8] Feng D， Feng M Q， Ozer E， et al. A vision-based sensor for noncontact structural displacement measurement [J]. Sensors， 2015， 15（7）： 16557-16575.

[9] Dong C Z， Celik O， Catbas F N， et al. A robust vision-based method for displacement measurement under adverse environmental factors using spatio-temporal context learning and Taylor approximation[J]. Sensors， 2019， 19（14）： 3197.

[10] Zhang Z Y. A flexible new technique for camera calibration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000， 22（11）： 1330-1334

[11] 高 翔， 張 涛. 视觉SLAM十四讲： 从理论到实践[M]. 北京： 电子工业出版社， 2017.

GAO Xiang， ZHANG Tao. Visual SLAM Lecture 14： From Theory to Practice[M]. Beijing： Publishing House of Electronics Industry， 2017.

[12] Zhang K， Zhang L， Liu Q， et al. Fast visual tracking via dense spatio-temporal context learning [C]. Proceedings of the European Conference on Computer Vision， Zurich， 2014： 127-141.

[13] Chan S H， V? D T， Nguyen T Q. Subpixel motion estimation without interpolation [C]. Proceedings of the International Conference on Acoustics， Speech and Signal Processing， IEEE， 2010： 722-725.

[14] Khuc T. Computer vision based structural identification framework for bridge health monitoring [D]. Florida： University of Central Florida， 2016.

作者简介： 周 洲（1996-），男，硕士研究生。电话：13060858565;E-mail：947665753@qq.com

通讯作者： 陈太聪（1977-），男，博士，副教授。电话：13903019936;E-mail：cvchentc@scut.edu.cn