承插式混凝土管道爆破振动动力响应尺寸效应研究
2021-12-16黄一文蒋楠周传波罗学东姚颖康夏宇磬
黄一文 蒋楠 周传波 罗学东 姚颖康 夏宇磬
摘要: 为研究爆破振动作用下不同内径规格承插式混凝土管道振动响应存在的尺寸效应,通过现场邻近管道爆破试验及其振动监测数据验证,结合动力有限元软件建立多尺寸管道爆破动力数值计算模型,分析承插式混凝土管道爆破振动响应特征;基于量纲分析基本理论,考虑管道尺寸效应影响建立管道爆破振动速度预测模型;结合混凝土的动抗拉强度,提出了不同内径混凝土管道的爆破振动速度控制标准。研究结果表明:管身和管道承插口峰值应力的出现存在时间差,管身峰值应力大于管道承插口,并随着管道内径的增加,两者峰值应力差值逐渐降低;在爆破地震波作用下,混凝土管道峰值振动速度随着管内径的增加而逐渐降低。
关键词: 爆破振动; 管道尺寸; 动力响应; 承插式混凝土管道; 安全判据
中图分类号: U455.6 文献标志码: A 文章编号: 1004-4523(2021)05-0969-10
DOI:10.16385/j.cnki.issn.1004-4523.2021.05.010
引 言
城区复杂环境下埋地管道工程交错纵横、环境复杂多变。承插式混凝土管道具有强度高、抗渗性好、抗外压能力强、生产效率高等优点,被广泛应用于城市给排水工程中。同时,近年来随着城市交通迅速发展,地铁等地下工程建设大量兴起,这些工程常与既有地下管道并行、交叉、跨越。爆破作为地下工程建设坚硬岩体重要的开挖手段,施工产生的地震波不可避免地对邻近混凝土给排水管道的安全性和可用性产生严重影响。保证爆破施工邻近承插式混凝土管道的安全运行,研究爆破振动作用下管道响应特征及其爆破振动安全判据具有重要的理论研究及实际应用价值。
目前,对于爆破振动荷载对邻近管道的影响,众多学者已开展了相关研究工作[1?3]。其中,在管道爆破振动响应影响因素研究方面,刘建民等[4]利用ANSYNS/LS?DYNA软件分析了炸药设置方式、炸药用量、爆心距和管道管径等因素对埋地管道损伤的不同作用。钟冬望等[5]在理论分析的基础上,通过对埋地无缝钢管进行现场爆破实验得出了应变峰值与爆心距和药量计算公式。在管道爆破振动安全判据研究方面,郝郁清等[6]结合管道最大容许应变计算出在已知装药量的条件下爆破施工时的最小安全距离。张紫剑等[7]通过现场监测试验,并对峰值振速进行拟合分析,得出不同频率下的爆破振动安全允许峰值振速。张震等[8]采用现场监测和动力有限元数值模拟相结合的研究方法,对超浅埋地铁站通道爆破开挖附近埋地混凝土管道的动力响应进行研究,提出保证管道安全的地表爆破控制振速。高坛等[9]通过数值模型计算和理论分析得到相应的管道爆破振动速度安全阈值。张黎明等[10]以管道的最大容许轴向应变峰值为管道的破坏判据,得到埋地钢管在不同主频下的安全允许峰值振速。综合分析已有研究成果可知,混凝土管道的爆破响应数值模拟研究中往往忽略管道承插口和管道尺寸的影响。事实上,城市市政中采用的承插式混凝土排水管尺寸规格在主线和支线上大有区别,在管道尺寸效应影响下管道爆破振动响应往往存在较大差异性。
为此,本文以武汉市城区典型土层埋置的给排水管道系统为工程依托,通过全尺度预埋承插式混凝土管道现场爆破试验,结合ANSYS/LS?DYNA有限元动力软件建立爆破振动作用下埋地混凝土管道的数值计算模型,分析了承插式混凝土管道在爆破地震波作用下的应力变化规律。基于量纲分析,研究了在管道尺寸效应影响下的管道上方地表土体和管道振速的变化规律,并依据混凝土构件的动抗拉强度来确定不同管道直径的承插式混凝土管道的振动速度安全判据。
1 邻近管道现场爆破试验
1.1 试验场地条件及混凝土管埋设
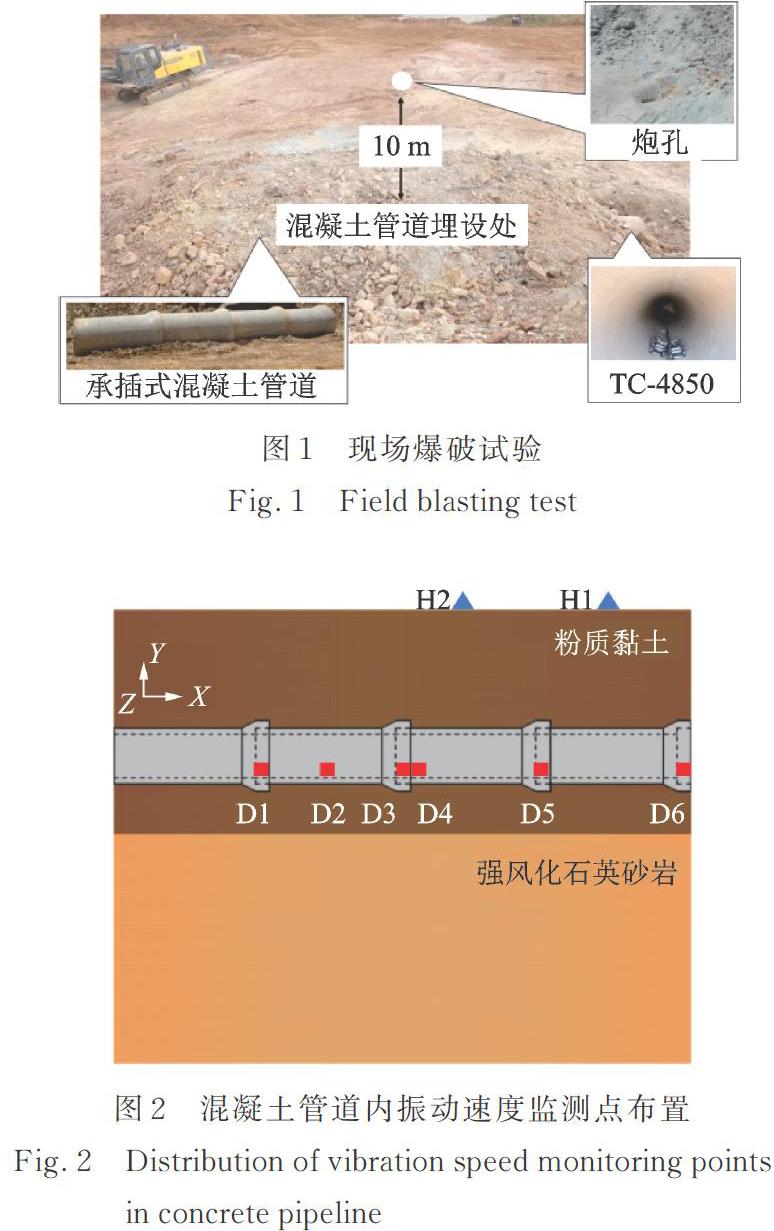
为研究承插式混凝土管道的爆破振动动力响应,对武汉市现有的排水管道附近的岩土爆破开挖工程进行大量调研,根据统计数据可知,武汉市采用的排水管道多为混凝土管道,管径主要在700?1600 mm之间,排水管道多埋置在粉质黏土以及杂填土中。本次试验选取的试验场地位于武汉市经济开发区硃山路与硃山一路交汇处,爆破所在地地质情况主要为强风化石英砂岩。管道覆土及垫土均为粉质黏土,现场管道埋设及炮孔位置如图1所示。
现场试验使用的承插式混凝土管道符合混凝土和钢筋混凝土管道国家標准要求[11],管道内径1 m,外径1.2 m;采用柔性接头B型承插口管接头,接头处设置止水橡胶圈;共使用4节管道,每节管道长2.5 m。为模拟城市承插式混凝土管道埋设条件,现场使用机械挖掘出管道沟槽,沟槽深3.6 m,垫土高0.4 m,上覆黏土厚度为2 m。组装承插式混凝土管道后,按照给水排水管道工程施工及验收标准规范要求分层夯实垫土层至地表标高,并确保槽底至管道顶部以上500 mm范围内,土中不含大于50 mm的砖、石等硬块[12]。在试验过程中,承插式混凝土管道不做加压处理,只考虑承插式混凝土管道在无水状态下爆破地震波作用下的动力响应。
1.2 管道振动速度监测和现场爆破方案
埋地管道在爆破地震波作用下的动力响应,主要表现为管道的振动特征和应力应变特征变化。本试验将混凝土管道的振动速度作为主要的监测和研究对象。
根据研究需要,本试验中采用爆破振动速度监测仪TC?4850,承插式混凝土管道在沟槽内安装完毕后,将振动速度传感器沿混凝土管道底部轴向布设,并进行固定,确保传感器在试验过程中保持稳定,共设置6个监测点:D1,D2,D3,D4,D5,D6,如图2所示,并通过信号输入抗干扰接头与爆破振动速度监测仪TC?4850相连。
如图1所示,在距混凝土管10 m处采用机械进行垂直钻孔,炮孔直径9 cm,炮孔深度为6 m,现场采用2#岩石乳化炸药进行爆破试验,炸药总质量为8 kg,采用单孔集中装药,并用炮泥进行堵塞,待混凝土管道安装埋设、监测装置安装完毕后,采用非电导爆管进行单孔单段起爆。
2 数值计算建模及其验证
2.1 模型介绍
由于现场试验条件有限,未进行不同尺寸承插式混凝土管道的现场爆破试验,采用ANSYS/LS?DYNA有限元动力软件建立承插式混凝土管道爆破振动数值计算模型,对混凝土管道的爆破振动动力响应尺寸效应进行研究。
根据现场试验,建立爆源与混凝土管道水平距离为10 m的数值计算模型。模型尺寸为21.2 m(长)10 m(宽)8 m(高),通过对几种不同网格划分方案进行比选,为保证数值计算的正常进行以及计算的精度,将土体及岩体的网格尺寸控制在20 cm,将混凝土管道网格按照每环40个进行划分,将炸药块体等分成10个单元。为模拟承插式混凝土管道的实际工作情况,按照实际尺寸建立承插式混凝土管,分段建立4节管段,然后设置接触,并在混凝土管道接触间设置橡胶,4节管道总长10 m,爆心距为10 m,炮孔深6 m,装药长度为1.06 m,炮泥长度为4.94 m,如图3所示。为模拟实际情况,管道与土层之间采用面面接触,设置摩擦系数为0.15;其他参数为默认值,在模型顶面定义为自由面,其余面则定义为无反射边界。
2.2 材料模型和算法介绍
模型中的材料包括岩层、土层、混凝土管道等,具体参数如表1所示。岩体介质是非连续、不均匀的,为简化处理,本文中的数值模拟将岩土体假设为均匀介质的弹塑性材料。根据现场地质资料,该地区岩层以强风化石英砂岩为主,采用*MAT_PLASTIC_KINEMATIC材料模型[13]。试验场地沟槽内覆土及垫土为粉质黏土,采用*MAT_ DRUCKER_PRAGER材料模型[13]。在众多混凝土动态模型中,*MAT_JOHNSON_HOLMQUIST_CONCRETE模型可用于模拟大应变、高应变率和高压下的混凝土[13],并被广泛应用于混凝土动载问题。在本数值计算模型中采用该模型对混凝土管道进行模拟。在混凝土承插口处设置橡胶圈,橡胶圈的材料采用*MAT_MOONEY?RIVLIN_RUBBER模型。为模拟现场试验中炮孔的炮泥堵塞,数值计算模型中炮泥采用*MAT_ PLASTIC_KINEMATIC材料模型[13]。
现场试验中爆破采用2#岩石乳化炸药,单孔连续装药量为8 kg。采用LS?DYNA软件自带的高能炸药材料*MAT_HIGH EXPLOSIVE_BURN来模拟炸药模型[13],炸药密度为1150 kg/m?,炸药爆速4000 m/s,同时参考相关文献[14],二号岩石乳化炸药计算参数取值如表2所示。JWL方程可以对炸药的爆轰压力与相对体积和内能的关系进行描述[15],可通过状态方程参数控制不同的炸药材料,如下式所示
式中 V为爆轰产物的相对比容;e为爆轰产物的比内能;A,B,R1,R2,ω为特征参数。
炸药采用ALE算法,ALE算法允许炸药、岩石和空气自由穿梭于彼此间,通过物质的流动可以分析爆炸发生的过程。其能够很好地避免计算中网格变形过大导致的计算中断问题。因此,ALE算法能够很好地应用于爆炸分析计算中[16]。土壤、岩石、混凝土、炮泥、橡胶等结构采用拉格朗日算法,该算法多用于固体结构的应力应变分析,这种方法以物质坐标为基础,其所描述的网格单元将以类似‘雕刻的方式划分在用于分析的结构上,主要的优点是能够非常精确地描述结构边界的运动。炸药与土体相互作用利用流固耦合算法来实现,通过添加流固耦合关键字进行处理。
2.3 数值模拟结果验证
为验证数值模拟计算结果是否合理,在管内径为1 m的模型中选取和现场试验振速监测点相同位置的监测点D1,D2,D3,D4,D5和D6,对所选取的监测点X,Y和Z方向的振动速度进行监测,同时和现场监测数据进行对比,如表3所示;并将同一条件下现场实测和数值模拟监测点D3的Z方向振速波形对比如图4所示。
由表3和图4可知:数值计算结果和现场监测数据误差率的平均值为7.65%。数值计算结果和现场监测的振动速度时程曲线变化基本吻合,可见数值模拟以及计算材料参数、算法的选取较为合理。并且由表3可知,三个方向中的Z方向振动速度最大,X方向次之,Y方向最小。在6个监测点位中D3和D4的振动速度最大,即管道中部位置。并且振动速度向混凝土管道两端逐渐降低。
3 反映混凝土管道尺寸效应的爆破振动预测模型
爆破地震波在岩土体内传播过程中,地震波的衰减受到的影响因素较多,文献[17?20]研究了爆破地震波在不同条件下的衰减规律。传播路径介质(岩土体的性质、岩体节理面等)、爆源的强度、爆源到监测点的距离、地形地貌是影响爆破地震波传播衰减的主要因素。考虑现场试验的条件将混凝土管内径影响下的爆破地震波传播衰减规律所涉及的主要变量进行归納,如表4所示。
由量纲分析白金汉定理(π定理)(Langhaar, 1951),地表岩土体质点峰值振动速度v可表示为
式(10)中:k3,k4,α2,β1分别为函数变换过程中给定的系数;式(11)中:-α2ln r表示爆破振动速度随距离r的变化;α2为衰减指数,主要反映场地介质条件的影响;而k3+(α2lnQ)/3综合反映了传播路径介质条件与炸药量对岩土体质点振动的贡献。
由上可以得到
式中 k为场地影响系数;α2表示为爆破振动衰减系数;β2为混凝土管内径影响下的效应系数。
4 承插式混凝土管道爆破振动响应特性分析
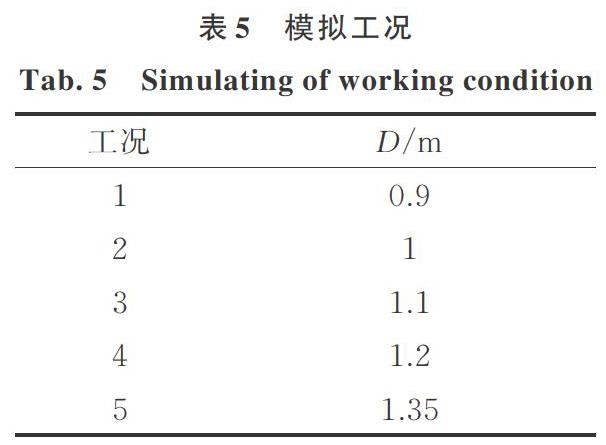
在城市的混凝土管道设施建设中,市政中排水管道在主线中尺寸较大,而支线管道尺寸较小。为分析承插式混凝土管道不同的直径对管道上方地表土以及管道爆破振动响应的影响,在只改变管内径的情况下共进行5种不同工况的数值模拟(其中D为承插式混凝土管的内径),如表5所示。
4.1 不同内径承插式混凝土管道应力分析
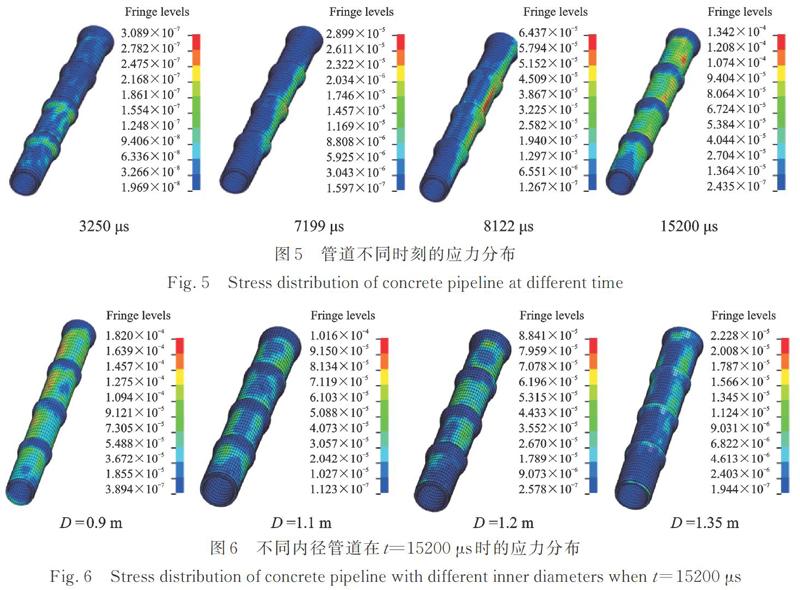
图5显示了管内径为1 m模型中混凝土管在不同时刻的应力分布。在选取的分析时间中,在3250 μs时,和爆源正对方向的管道承插口和临近承插口的位置处最先出现较高应力;在7199 μs时,爆源正对方向管道承插口最大应力达到2.234 MPa,随着时间的变化,混凝土管道应力进一步增大,并从管道中部位置沿轴线向两端扩展;在8122 μs时,最大应力出现在爆源正对方向管道承插口附近管节的中部位置,最大应力达到5.324 MPa;在15200 μs时,应力区向管道环向进一步扩展,管道承插口处应力降低,管身位置出现高应力区。
将其他内径的混凝土管道在15200 μs时迎爆侧应力分布图与内径为1 m的模型进行对比,如图6所示。随着管径的增大,高应力区以及最大应力值减少,在管内径为1.35 m时,最大应力值急剧减少为1.125 MPa。
结合图5和6可知,在爆破地震波作用下,承插式混凝土管道在振动响应过程中高应力区主要集中在迎爆侧。在不同内径承插式混凝土管道的迎爆侧,如图7所示选取6个监测点位,读取每个监测点的峰值应力进行对比,如图8所示。内径为0.9 m的承插式混凝土管道管身出现的峰值应力最大为13.51 MPa,承插口出现的峰值应力最大为3.62 MPa,管身和承插口应力差值存在较大差值,随着承插式混凝土管道管径的增大,监测点的峰值应力急剧降低,承插口与管身的峰值应力差值降低,当管径达到1.35 m时,承插式混凝土管道管身出现的峰值应力最大为0.91 MPa,承插口出现的峰值应力最大为0.78 MPa,承插口与管身峰值应力基本趋于一致。在爆破地震波作用下,承插式混凝土管道应力最大值出现在监测点1和点3位置,由此可确定监测点1和点3所在截面为承插式混凝土管道在爆破地震波作用下的危险截面。
4.2 不同内径承插式混凝土管道振速分析
为分析5种不同工况下承插式混凝土管道危险截面处的动力响应特征,将图7中点1和点3所在的危险截面等分为12部分,用以观察管道截面不同位置的质点峰值振动速度,如图9所示,承插式混凝土管道的迎爆侧即270°?360°位置处的质点峰值振速最大,随着与爆源距离的增加,质点的峰值振动速度逐渐降低。随着管道内径的增加,危险截面上的质点峰值振动速度逐渐降低。管道内径为0.9 m时,迎爆侧质点峰值振动速度最大为22.40 cm/s;当管径增加到1.35 m时,迎爆侧质点峰值振动速度最大值降低至6.65 cm/s,减少了70.3%。由此可知,在研究爆破地震波作用下管道的动力响应问题时,应该考虑管道尺寸这个影响因素。
4.3 管道上方地表土体在管道内径影响下的爆破振动规律
在不同管道内径的数值计算模型中,如图2所示,在承插式混凝土管道的危险截面处正上方地表土体选取监测点位H1和H2,由于爆源和测点连线方向即Z方向的振动速度最大,故只对测点Z方向的振速进行了统计,不同管内径模型的爆破振动数据如表6所示。由表6可知,随着混凝土管半径以及测点和爆源间距离的增大,模型中地表监测点Z方向的峰值振动速度依次递减。
采用考虑混凝土管半径影响的地表土体爆破振动速度规律的数学模型式(13)对表6中所列测试结果进行回归分析,得到混凝土管内径影响的地表土体爆破振动规律的预测模型,结果如下式所示
式中 v为管道上方土体峰值振动速度,D为管道内径,相关系数R2=0.950,可靠度较高,能比较好地反映v和D之间关系。由式(14)可知,当测点与爆源距离一定时,管道上方土体峰值振速振速随着管内径的增加而逐渐降低。
5 基于管身破坏的管道振动速度安全判据
5.1 管道和上方地表土体振速对比分析
由于管道埋置于地下,现场工程条件下不便于进行开挖揭露。 参考朱斌军等[21]将管道上方地表振动速度作为更加直观的爆破振动观测值,对管道与正上方地表X,Y,Z合方向振速进行线性统计。在每个模型中选取混凝土管正上方土体表面H1,H2处和对应管道截面上的Z方向的峰值振动速度进行线性拟合,结果如图10所示。
承插式混凝土管道和正上方地表土体Z方向峰值振动速度统计关系为
式中 v1为承插式混凝土管道危险截面上最大Z方向的峰值振动速度(cm/s); v为管道正上方地表土体Z方向的峰值振动速度(cm/s)。由图10可知,混凝土管道危险截面峰值振速大于正上方地表土体,这是由于混凝土管道与爆源间的距离较小,随着与爆源之间距离的增加,爆破振动响应也随之降低,管道和土体结构的不同也导致在爆破地震波作用下,两者的振动响应有所区别。由式(15)可知,混凝土管道危险截面上最大的Z方向峰值振动速度与正上方地表土体呈线性关系,随着地表土体峰值振速的增加而增加。结合式(14)可知,当测点与爆源距离一定时,管道内部Z方向的峰值振动速度随着管内径的增加而逐渐降低。这是由于随着混凝土管道内径的增加,管土间的接触面积也随之增加,周围土体对混凝土管的约束作用也随之增强,从而导致混凝土管道在爆破地震作用下的峰值振动速度降低。
5.2 管道单元拉应力与峰值振速关系
混凝土材料的抗压强度较大,而抗拉强度较小,在爆破振动响应中,混凝土管道主要是产生受拉破坏[22]。在动态荷载作用下,不考虑应变速率时,混凝土结构的极限动抗拉强度取2.099 MPa[23],参考混凝土结构设计规范中给出的C35混凝土轴心抗拉强度标准值?tk=2.20 MPa,混凝土轴心抗拉强度设计值?t=1.57 MPa[24]。取a=?tk/?t=1.40为混凝土结构极限动抗拉强度的修正系数,得到混凝土管道在正常使用条件下的极限动抗拉强度?=1.50 MPa。
工程实际表明,混凝土管道爆破振动破坏主要为爆破地震波在管道介质中傳播引起的管道应力变化而产生的管道材料本身的失效破坏。根据波动学理论,波在无限介质中传播时产生的应力可按照下式计算
式中 σ为正应力(MPa);ρ为传播介质密度(g/cm3);c为波在介质中的传播速度,按照波的类型可以分为纵波和横波(cm/s);v为波传播过程中引起的介质质点的振动速度(cm/s)。本研究中,爆破地震波在管道中传播引起管道单元应力的变化,管道传播介质一定,因此介质密度ρ以及波的传播速度c可以近似看作定值,所以ρc可以看作常数k,故上式可以变为应力与速度相关的一次函数。此外,有学者也以该理论为基础,通过应力与速度得到一次函数关系来分析管道的安全性[25]。
在每种工况中,将承插式混凝土管道危险截面上的峰值拉应力和峰值振速进行线性拟合,统计关系如表7所示。根据表7中管道峰值拉应力σt和峰值振动速度v2的统计关系,由混凝土管道正常使用条件下的极限动抗拉强度?可到不同内径混凝土管的振动速度安全判据,如表8所示。
由表8可知,在保证混凝土管道正常使用的条件下,混凝土管道内径的不同,管道在爆破地震波作用下的控制振速也有所不同,并随着管内径的增加,承插式混凝土管道的振动速度最大安全允许值逐渐减小。
6 结 论
本文通过承插式混凝土管道在爆破振动作用下的动力响应现场试验,并结合数值计算模型进行工况补充,得到了不同尺寸承插式混凝土管道在爆破振动作用下的动力响应结果如下:
(1)在爆破地震波的作用下,承插式混凝土管道的管身和管道承插口出现不同的应力响应,峰值应力出现的时间存在差别,管身产生的峰值应力大于管道承插口,并随着管道内径的增加,管道產生的峰值应力降低,管身和承插口的峰值应力差值也随之降低。
(2)基于量纲分析,结合数值计算模型的数据,得到在管道尺寸影响下的管道爆破振动速度的变化规律。混凝土管道在爆破地震波的作用下,产生的峰值振动速度随着管道内径的增加而逐渐降低。
(3)随着管道内径的增加,以承插式混凝土管道在爆破振动作用下受拉破坏为判别依据,混凝土管道在爆破振动作用下安全使用的最大振动速度逐渐降低。内径为0.9,1,1.1,1.2,1.35 m的承插式混凝土管道的爆破振动速度控制阈值分别为23.41,22.95,19.77 ,16.66 ,14.17 cm/s。
参考文献:
[1] AMIR Sajjad Abedi, NADER Hataf, ARSALAN Ghahramani. Analytical solution of the dynamic response of buried pipelines under blast wave[J]. International Journal of Rock Mechanics and Mining Sciences, 2016,88:201-306.
[2] Zhang L, Liang Z, Zhang J. Mechanical response of a buried pipeline to explosion loading[J]. Journal of Failure Analysis and Prevention, 2016,16(4): 576-582.
[3] 郑爽英,杨立中.隧道爆破地震下输气管道动力响应数值试验[J].西南交通大学学报,2017,52(2):264-271.
Zheng S Y, Yang L Z. Numerical experiments of dynamic response of buried gas pipeline under the action of seismic waves induced by tunnel blasting[J]. Journal of Southwest Jiaotong University, 2017, 52(2):264-271.
[4] 刘建民,陈文涛.爆炸荷载下埋地管道动力响应分析研究[J].工程爆破, 2008,14(2):20-24.
Liu J M, Chen W T. Dynamic response study of buried pipeline subjected to blast loads[J]. Engineering Blasting, 2008,14(2): 20-24.
[5] 钟冬望,黄 雄,司剑峰,等.爆破荷载作用下埋地钢管的动态响应实验研究[J].爆破, 2018,35(2):19-25.
Zhong D W, Huang X, Si J F,et al. Experimental study on dynamic response of buried pipeline under blasting loads[J].Blasting, 2018,35(2):19-25.
[6] 郝郁清,程 康,赵其达拉图,等.爆破地震波作用下燃气管道的安全距离研究[J].爆破, 2018,35(2):137-143.
Hao Y Q, Cheng K, Zhao Q D L T, et al. Study on safety distance of gas pipeline under action of blasting seismic wave[J]. Blasting, 2018,35(2):137-143.
[7] 张紫剑,赵昌龙,张黎明,等.埋地管道爆破振动安全允许判据试验探究[J].爆破, 2016,33(2):12-16.
Zhang Z J, Zhao C L, Zhang L M, et al. Experimental investigation of blasting vibration safety criterion on buried pipeline[J]. Blasting, 2016,33(2):12-16.
[8] 张 震,周传波,路世伟,等.爆破振动作用下邻近埋地混凝土管道动力响应特性[J].哈尔滨工业大学学报, 2017,49(9):79-84.
Zhang Z, Zhou C B, Lu S W , et al. Dynamic response characteristic of adjacent buried concrete pipeline subjected to blasting vibration[J].Journal of Harbin Institute of Technology, 2017,49(9):79-84.
[9] 高 壇,周传波,蒋 楠,等.基坑开挖爆破下邻近管道振动速度安全阈值研究[J].安全与环境学报, 2017,17(6):2191-2195.
Gao T, Zhou C B, Jiang N, et al. Study on the vibration velocity thresh-old of the adjacent pipeline under the blasting excavation of the foundation pit [J]. Journal of Safety and Environment, 2017,17(6):2191-2195.
[10] 张黎明,赵昌龙,池恩安,等.地下管道爆破振动安全允许峰值振速试验研究[J].爆破, 2019,36(4):146-149+154.
Zhang L M, Zhao C L, Chi E A, et al. Experimental investigation on allowed blasting vibration velocity of underground pipeline [J]. Blasting, 2019,36(4):146-149+154.
[11] 沈丽华,王贯明,王憬山,等. GB/T 11836-2009,混凝土和钢筋混凝土排水管[S]. 北京: 中国标准出版社,2009.
Shen Lihua, Wang Guanming, Wang Jingshan, et al. GB/T 11836-2009, Concrete and reinforced concrete sewer pipes[S]. Beijing: Standards Press of China, 2009.
[12] 中华人民共和国住房和城乡建设部. GB 50268-2008,给水排水管道工程施工及验收规范[S] . 北京: 中国建筑工业出版社,2008.
MOHURD. GB 50268-2008,Code for construction and acceptance of water and sewerage pipeline works[S]. Beijing: China Architecture & Building Press, 2008.
[13] HALLQUIST J. LS-DYNA Keyword Users Manual R8.0[M]. California: Livermore Software Technology Corporation,2015.
[14] Xie L X, Lu W B, Zhang Q B, et al. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2016, 58, 257?270.
[15] 赵 铮,陶 钢,杜长星.爆轰产物JWL状态方程应用研究[J].高压物理学报, 2009,23(4):277-282.
Zhao Z, Tao G, Du C X. Application research on JWL equation of state of detonation products[J]. Chinese Journal of High Pressure Physics, 2009,23(4):277-282.
[16] 王峥峥,张杨生.基于ALE算法的隧道开挖爆破振动特性数值分析[J].大连理工大学学报,2017,57(3):279-284.
Wang Z Z, Zhang Y S. Numerical analysis for blasting vibration characteristics in tunnel excavation based on ALE algorithm[J]. Journal of Dalian University of Technology, 2017,57(3):279-284.
[17] 李继业,蒲朝钦,何兴贵.节理岩体边坡爆破振动衰减特征分析[J].爆破, 2018,35(2):32-36.
Li J Y, Pu C Q, He X G. Analysis of blasting vibration attenuation characteristics of jointed rock mass slope [J]. Blasting, 2018,35(2):32-36.
[18] 唐 海,李海波,蒋鹏灿,等.地形地貌对爆破振动波传播的影响实验研究[J].岩石力学与工程学报, 2007,26(9):1817-1823.
Tang H, Li H B, Jiang P C, et al. Experimental study on effect of topography on propagation of blasting waves[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(9):1817-1823.
[19] 王智德,江俐敏,祝文化,等.顺层岩质边坡爆破荷载作用下的振动传播规律研究[J].爆破, 2019,36(1):55-62.
Wang Z d, Jiang L M, Zhu W H, et al. Vibration Propagation Characteristics of Bedding Rock Slope under Blasting Loads[J]. Blasting, 2019,36(1):55-62.
[20] 吕 涛,石永强,黄诚,等.非线性回归法求解爆破振动速度衰减公式参数[J].岩土力学, 2007,28(9):1871-1878.
Lu T, Shi Y Q, Huang C, et al. Study on attenuation parameters of blasting vibration by nonlinear regression analysis[J]. Rock and Soil Mechanics, 2007,28(9):1871-1878.
[21] 朱 斌,蒋 楠,贾永胜,等.下穿穿燃气管道爆破振动效应现场试验研究[J].岩石力学与工程学报,2019,38(12):2582-2592.
Zhu B, Jiang N, Jia Y S, et al. Field experiment on blasting vibration effect of underpass gas pipelines[J].Chinese Journal of Rock Mechanics and Engineering, 2019,38(12):2582-2592.
[22] 夏宇磬,蒋 楠,姚颖康,等.粉质黏土层预埋承插式混凝土管道对爆破振动的动力响应[J].爆炸与冲击, 2020,40(4):73-83.
XIA Y Q, Jiang N, Yao Y k, et al. Experiment study on dynamic response of spigot concrete pipe buried in silty clay layer subjected to blasting seismic wave[J]. Explosion and Shock Waves, 2020,40(4):73-83.
[23] Jin X, Hou C, Fan X, et al. Quasi-static and dynamic experimental studies on the tensile strength and failure pattern of concrete and mortar discs [J].Scientific Reports, 2017,7(1):15305.
[24] 中華人民共和国住房和城乡建设部. GB50010-2010,混凝土结构设计规范(2015版) [S]. 北京: 中国建筑工业出版社,2015.
MOHURD. GB50010-2010, Code for design of concrete structures (2015) [S]. Beijing: China Architecture & Building Press, 2015.
[25] 朱 斌,蒋 楠,周传波,等.基坑开挖爆破作用邻近压力燃气管道动力响应特性研究[J].振动与冲击, 2020,39(11):201-208.
Zhu B, Jiang N, Zhou C B, et al. Effect of excavation blast vibration on adjacent buried gas pipeline in a foundation pit[J]. Journal of Vibration and Shock, 2020,39(11):201-208.
作者简介: 黄一文(1995-),男,硕士研究生。电话:17635076978;E- mail:h2428948778@163.com
通讯作者: 蒋 楠(1986-),男,博士,副教授。电话:18164055091;E-mail:happyjohn@foxmail.com
