“找次品”教学“误区”简析
2021-12-16钟淑燕
钟淑燕
“找次品”是人教版五年级数学下册第八单元的内容。本单元以“找次品”这一探索性操作活动为载体,让学生通过观察、猜测、试验等方式探索解决问题的策略。同时,进一步理解随机事件(如2个零件中有1个较重的次品,只要把这2个零件放在天平两端,天平一定不平衡。如果3个零件中有1个较重的次品,任意取2个放在天平两端,天平可能平衡,也有可能不平衡),感受解决问题策略的多样性和优化思想,培养观察、分析、逻辑推理的能力,并学习如何用直观的方式清晰、简洁、有条理地表示逻辑推理过程。在教学中,如何清晰地表达数学思维的过程,如何理解解决问题策略的多样化和优化,如何运用“比较—猜想—验证”的策略发现数学结论,如何把复杂问题转化为简单的问题,如何把具体问题推广为一般问题,都是在解决问题过程中需要考虑的。这些蕴含在解决问题过程之中的隐性的“形成性能力”或许恰恰是过去数学教育中容易忽视的,教师在日常教学中能否重视这些能力的培养,直接决定了学生综合能力的高低。并且,这些能力的获得不仅局限于促进数学学习,甚至可以延伸至其他学科,乃至未来学习、生活和工作的方方面面。在设计教学时,我们要注意以下“误区”:
误区一:利用实物天平进行试验,可以使教学过程更直观
某教师在教学时,为了使教学过程直观形象,课堂开始就让学生4个一组用实物天平称“零件”,从3个“零件”中找出较轻的“次品零件”。学生在试验过程中,每一次称时,都需要对天平进行调节与处理,一个简单的试验,耽误了一半的课堂时间,而且有的小组看不清楚,实验效果也不明显。很多教师在教学本课之初,受课本情境图的影响,或多或少都走过类似的误区。由此,教师在教学时,都需要考虑一个问题:我们需要的工具应该是一架什么样的天平?
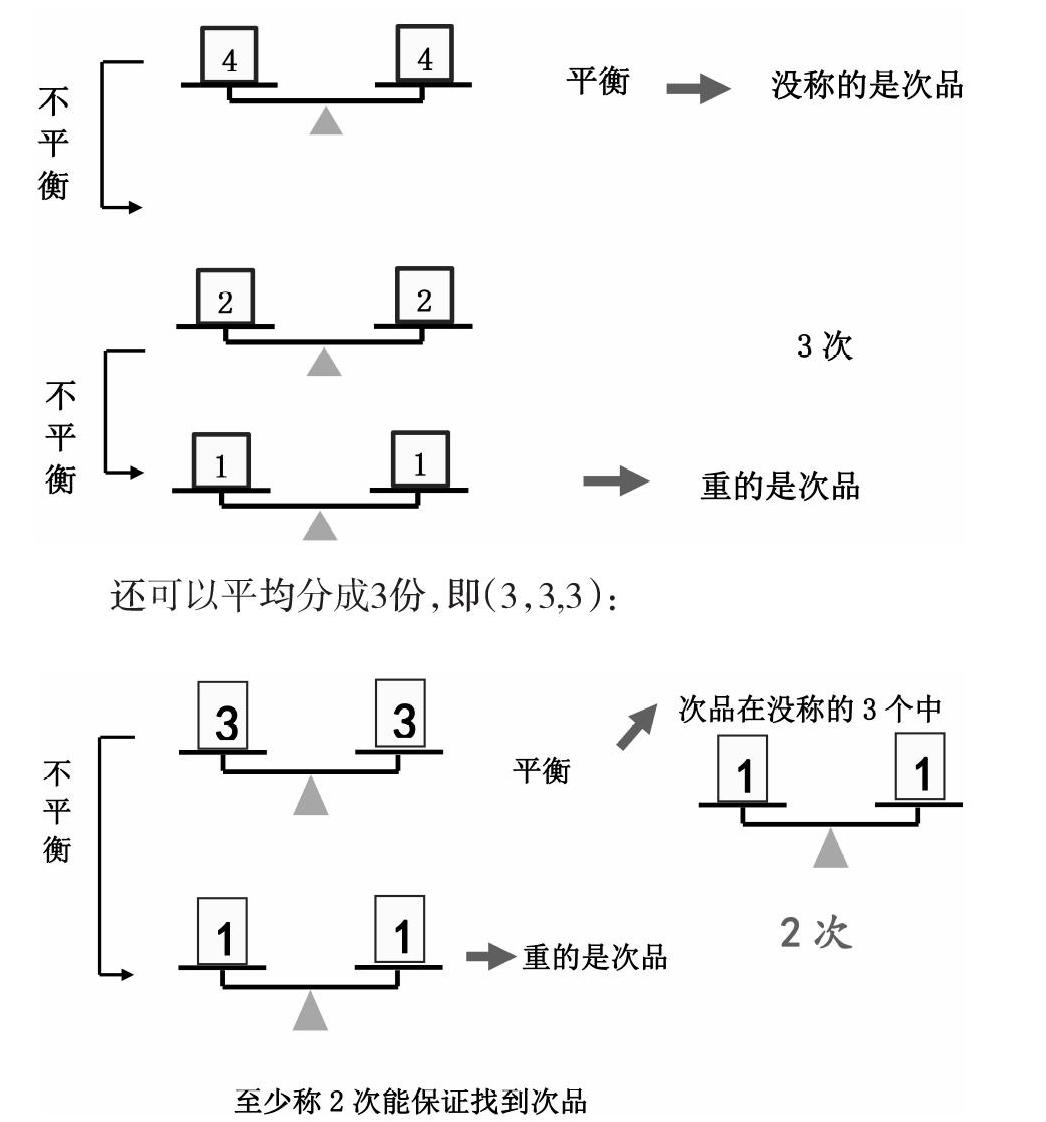
“找次品”问题中的天平,只能通过零件之间的称量进行比较,并不是一定要通过天平称,而是利用天平平衡的原理通过逻辑推理确定出次品。所以,在教学时,教师所用的天平并不是一架实物天平,而是一种抽象的数学化形式的天平。在解决问题的过程中,实际上是用头脑中建立的天平表象,反复地进行“如果平衡,那么……”“如果不平衡,那么……”的逻辑推理过程。当物品总量比较多时,步骤相应增加,很容易表述不清,如果仅用文字表达式,由于前后步骤之间的层层套叠关系,表述起来也显得冗长烦琐。教师可以引导学生使用直观图或流程图,配以相应的文字说明,可以比较简洁而又清晰地表示出逻辑推理的整个过程,让人一目了然。如:9个零件怎样称的次数最少找出次品呢?先可以这样分3份,即(4,4,1):
还可以平均分成3份,即(3,3,3):
让学生利用天平模型来直观演示和操作,这样不仅可以节约课堂教学时间,同时又训练了学生的逻辑推理,提升了学生的数学思维能力,为后面脱离具体的实物操作,实现从具体形象思维到抽象逻辑思维的过渡奠定了良好的基础。而如果用实物天平进行试验,不仅麻烦费时,也不会出现“假如平衡,那么……”“假如不平衡,那么……”的情况,只会出现其中一种,要么平衡,要么不平衡,達不到预期的教学目的。
误区二:“至少”“能保证”次数等于“运气好”的偶然次数
“至少称几次能保证找出次品”是理解的难点。在教学时,教师要帮助学生理解“至少”“能保证”的含义是关键,而不少教师则很纠结于如何向学生说清二者的含义,“至少”表示最少,但为了“保证找出次品”又要考虑不凑巧的情况——所需次数更多。要往“最少”想,又要考虑次数更多的情况,似乎有点矛盾,怎么向学生说清楚呢?如,找5个零件的次品问题中,第一次可以“1┬1”,也可以“2┬2”,如果在天平两端各放1个零件,假如不平衡,1次可以找出次品,假如平衡,2次可以找出次品;如果是第二种方法,在天平两端各放2个零件,假如天平平衡,次品就是外面的那个,1次就能找出次品。假如不平衡,次品就在翘起的2个中。再把翘起的托盘中的两个零件放在天平两边,翘起的那个就是次品。教师根据学生的椎理,板书“5(221)→2(11)”,称2次才能找出次品。呈现两种称法的两种结果,让学生思考:找出5个零件中的次品,至少要称几次才能保证找到次品?此时学生会出现争议:有的学生认为1次,有的学生认为2次。结合争议与思考,学生很容易理解,虽然1次比2次少,而称1次就找到次品是“运气好”,“运气不好”就找不到次品,属于偶然情况。而这里要求的是保证找到次品所用的最少次数,不能只考虑偶然情况,所以要“至少”称2次才能“保证找出次品”。进一步让学生明确“能保证”就是指每一条“可能的路径”都要考虑到,不能仅停留在“运气好”的情况;“至少”就是指在保证一定能找出次品的各种方法中,称量次数最少的那种方案。
“找次品问题”是数学中一类经典智力问题,吸引着众多数学爱好者孜孜不倦地寻求一般性解决方法。“找次品问题”又细分为许多类型,有的类型解决起来相当复杂,在探究过程中,教师要认真思考,引导学生“从简单问题入手”,会用符号记录问题解决的过程,将思维过程外显化,便于学生、教师之间的沟通交流,使不同层次的学生以符号语言为依托,为研究更为复杂的“找次品问题”提供了有效的交流保证。
