经历探索过程 发展空间观念
2021-12-16陈松兰
陈松兰
教学内容:
数学人教版五年级下册第三单元长方体、正方体表面积和体积练习。
教学目标:
1.进一步认识长方体和正方体的特征,理解长方体和正方体的表面积、体积(容积)的意义及其计算方法,并能够解决简单的实际问题。
2.经历切拼、包装等图形变换和操作活动,沟通形体之间的内在联系,丰富对图形的认识,发展空间观念。
3.在观察、想象、讨论、交流中,感受数学与生活的密切联系,进一步养成合作交流的习惯,体验数学学习的乐趣。
教学重难点:
熟练掌握不同长方体、正方体表面积和体积的计算方法。
教学过程:
一、激活基点,强化概念
1.提问:老师带来了铁丝、纸板、橡皮泥这三种材料,我想做一个长a、宽b、高h的长方体模型,请你帮我选择材料,并算一算需要多少材料?
2.全班交流,相机板书
(1)用铁丝做成的长方体是一个框架,所需材料就是要求这个长方体的棱长总和,即4(a+b+h)。
(2)用紙板做出来的长方体是一个空盒,所需材料就是要求这个长方体的表面积,长方体有6个面,相对的面面积相等,因此,需要纸板的面积为2(ab+ah+bh)。
(3)用橡皮泥做出来的长方体是一个实心的长方体,所需材料就是要求这个长方体的体积,即abh。
3.提问:如果要制作一个棱长为a的正方体模型,各需要多少材料?
4.小结引入
不同的材料构成了不同形态的长方体和正方体,计算需要多少材料,用到了棱长及其总和、表面积和体积知识。今天这节课我们继续研究长方体、正方体的表面积和体积。(板书课题)
思考:安排任务驱动,制作同一个长方体和正方体,根据选择的材料不同,求所需材料的数学实质和方法也不同。引入环节的师生合作顺势复习了长方体、正方体的棱长总和、表面积、体积,进行图形再认、形象想象及其数学要素的计算方法公式温习,同时培养了学生具象和抽象互换的空间想象和灵活解题的能力。这为本课其后的综合练习做了必要铺垫。
二、梳理构建,内化提升
提问:生活中的长方体,你见过哪几种类型?
预设:(1)6个面都是长方形的长方体。(2)有两个面都是正方形的长方体。(3)6个面都是正方形的特殊长方体——正方体。
师引入:那接下来我们就锁定这三类长方体进行研究,敢接受挑战吗?
(一)挑战一:设计一个6个面都是长方形的长方体
1.自由设计:请你设计一个6个面都是长方形的长方体,写出它的长、宽、高。(生设计交流)
2.提问:谁能概括一下该怎样设计?(任举长宽高数据,使之各不相等即可)
3.投影其面想象长方体。
(1)激疑:老师今天也带来了一个这类长方体,要知道它的长、宽、高是多少需要看到几个面?至少要看到几个面就能知道它的长、宽、高?(至少看2个面)
(2)想象:古人说得好:“纸上得来终觉浅,绝知此事要躬行”。请一名同学在大屏幕上点出长方体的两个面,其他同学迅速在头脑中还原或想象出这个长方体的模样,并写出长、宽、高。(多媒体演示)
(3)思考:除了看这两个面,看其他两个面行吗?这两个面有什么要求?(应是相邻的两个面,其中一定包含长、宽、高“三度”。)
(4)课件出示完整的长方体:长5cm、宽3cm、高4cm,生口答它的表面积和体积。
(二)挑战二:切出有两个面是正方形的长方体
1.提问:如果就利用第一类长方体,怎样能得到第二类有两个面是正方形的长方体呢?(可以切)
2.比画思考:观察刚才长5 cm、宽3 cm、高4 cm的长方体,要得到有两个面是正方形的长方体,只准切一刀怎么切?同学们可以借助身边的长方体比画比画。
3.交流发现,初步感知
师:请同学们结合长方体来比画一下怎么切?切成的长方体的长、宽、高各是多少?哪两个面是正方形?
结合学生发言课件演示三种切法:
第一种切法:高切掉1 cm,变成长5 cm、宽3 cm、高3 cm的长方体;
第二种切法:长切掉1 cm,变成长4 cm、宽3 cm、高4 cm的长方体;
第三种切法:长切掉2 cm,变成长3 cm、宽3 cm、高4 cm的长方体。
4.比较发现,思维提升
师:我们选择第一种切法继续研究,一刀切下去后这个长方体一分为二,在这个过程中长方体发生了哪些变化?你能提出哪些数学问题?
问题预设:
(1)切后体积变化了吗?两者的表面积之和增加了,增加了多少平方厘米?
(2)切成新的长方体表面积减少了,减少了多少平方厘米?
(3)切成新的长方体体积减少了,减少了多少立方厘米?
5.小结:梳理一下同学们的问题,主要关于体积和表面积这两类。同学们观察角度不同,“增加了”和“减少了”都有道理。
6.提问:刚才同学们发挥了聪明才智,用切的方法使得“三度”中有两者相等,就得到了第二类有两个面是正方形的长方体,还能切吗?我们继续挑战。
(三)挑战三:切出棱长最大的正方体
1.比画思考:从刚刚切好的三个长方体中任选一个,切成棱长最大的正方体,可以怎么切?(交流汇报)
2.比较发现:这三个长方体长得又不一样?为什么切成的最大正方体的棱长都是3 cm呢?(以最短边为基准,正方体的棱长最大是3 cm)
师:请口算它的表面积和体积。(生口答)
3.小结:同学们真厉害!三次全部挑战成功。对于长方体、正方体表面积和体积的知识,又进行了梳理和巩固。生活中的数学会有更多的挑战,想不想再试试身手?
思考:三次挑战活动从图形联系和运动、变化的角度,别开生面灵活组织练习,规避了孤立、静态的公式计算练习。这样构题灵活新颖,增加趣味性,充分激发了学生的探索热情;利用多媒体课件帮助演示,完善学生的想象空间。同时,强化图形间的联系认知思维,构建长方体、正方体知识网络体系,促进学生积累了解决问题的经验,发展思维品质,培养了良好的数学素养。
三、运用拓展,实践创新
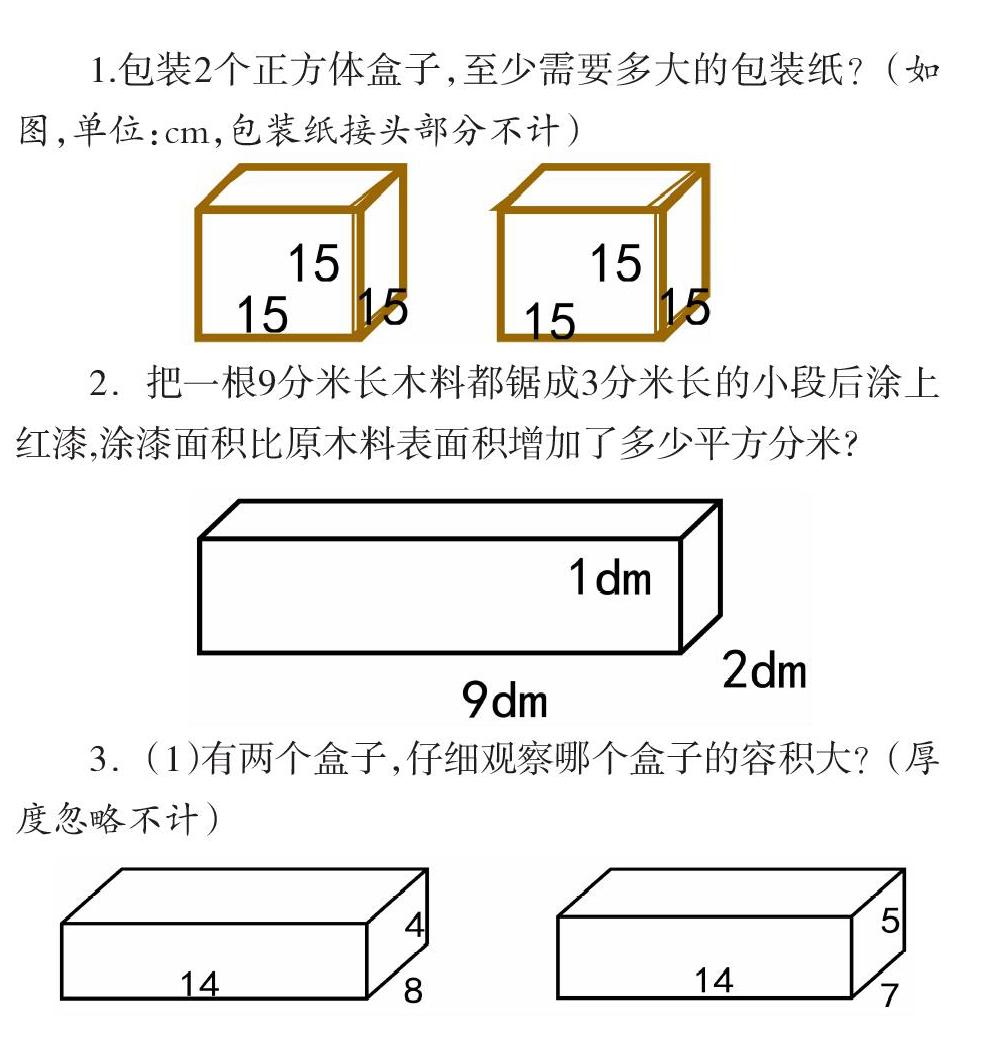
1.包装2个正方体盒子,至少需要多大的包装纸?(如图,单位:cm,包装纸接头部分不计)
2.把一根9分米长木料都锯成3分米长的小段后涂上红漆,涂漆面积比原木料表面积增加了多少平方分米?
3.(1)有两个盒子,仔细观察哪个盒子的容积大?(厚度忽略不计)
交流引导:直接比较侧面积,第二个盒子容积大。
(2)在这两个盒子里,装填的是棱长2 cm的小正方体,猜一猜,哪个盒子里装得多?
课件演示,交流得出第一个盒子装得多。
小结:用容积除以物体体积这种方法有局限性。容器装固体,要考虑大容器的棱长和所装小物体的对应棱长是否正好是倍数关系的情况。
四、全课总结,交流收获
今天的学习你有什么收获?解决问题的过程中有什么感受?还想到了什么新问题?
思考:从生活实践中开发资源,精心设计练习,运用包装、切割、涂漆、装填等实践问题的呈现,丰富学生的认知,使得长方体、正方体知识的运用变得更加具体、鲜活,促进深度学习,以进一步展开探索思维。空间想象能力是空间观念的重要体现。应用拓展部分的练习,让学生在解决这一系列实际问题过程中,获得了空间想象的舒展锻炼机会,操练了空间想象力发展的智能“体操”!
