钢化真空玻璃球形支撑的玻璃压痕应力场理论及分析
2021-12-16蔺海晓刘志红岳高伟
蔺海晓,刘志红,岳高伟
(河南理工大学土木工程学院,焦作 454000)
0 引 言
钢化真空玻璃作为新一代节能环保玻璃,具有其他种类玻璃无法比拟的隔热、隔声等优越性能[1-2],此外钢化真空玻璃充分利用了钢化玻璃强度高的优点,极大改善了真空玻璃的力学性能,还具有破碎后危害小等优点[3-5],成为国内外最具发展潜力的节能玻璃[6]。
钢化真空玻璃抽真空后,在玻璃外表面大气压的作用下,两片玻璃将向内变形,为防止两片玻璃中部贴在一起,在两片玻璃之间按一定规则布置了一系列支撑物,这些支撑物将两片钢化玻璃隔离,形成有效的真空层。而支撑物的排布方式(间距、排布形状等)对钢化玻璃的力学性能影响显著,缪宏等[7]、张瑞宏等[8]、邹惠芬等[9]、冯毅等[10]研究了不同支撑物在真空玻璃上的力学效应,并利用数值分析研究真空玻璃支撑柱的应力场,优化支承物的分布。刘小根等[11-12]对钢化真空玻璃的表面压痕做了深入研究,提出了真空玻璃在不产生压痕时的最大临界支撑力计算公式,并对真空玻璃支撑物缺失以及缺失量的应力及变形进行了分析。李彦兵等[6,13]利用数值分析研究了钢化真空玻璃支撑点排布方式和支撑间距对钢化玻璃力学性能的影响。以上研究虽然对钢化真空玻璃制造中支撑物排布方式和间距选取提供了理论依据,但是均未分析支撑物对玻璃产生的应力场,这会影响对玻璃使用寿命的准确分析。
因此,本文通过建立球形-玻璃板的压载模型,推导出赫兹压痕的应力场方程,计算分析钢化真空玻璃支撑物对玻璃的压痕及应力特征,以便更好地对钢化真空玻璃的使用寿命进行推测。
1 钢化真空玻璃受力分析及压痕
钢化真空玻璃是由两片平板钢化玻璃、封接焊料和支撑物组成(见图1),其中支撑物按一定序列排布在两片玻璃之间。
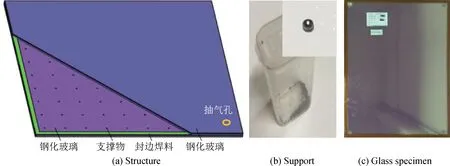
图1 钢化真空玻璃结构、支撑物及试件Fig.1 Toughened vacuum glass structure, support and specimens
在建立钢化真空玻璃模型分析时,对其作如下假设[13]:
(1)边界无位移假设。钢化真空玻璃边界采用固支约束,即边界无位移。
(2)弹性体假设。钢化玻璃所受荷载未超出极限时(90 MPa),表现出理想弹性的特性;当分析中应力超出这个极限时,即认为钢化玻璃破碎。
建立厚度4 mm、尺寸400 mm×400 mm的钢化真空玻璃模型,支撑物间距为50 mm×50 mm(见图2(a)),支撑物距玻璃边部距离25 mm,支撑物直径0.5 mm;封接焊料宽度0.7 mm,厚度0.5 mm。钢化玻璃弹性模量为72 GPa,泊松比为0.2,密度为2 500 kg/m3;封接焊料为合金材料(SnAgCu合金),经过试验确定,其弹性模量为29.04 GPa,泊松比为0.35,密度为7 340 kg/m3;支撑物为低碳钢材质的球体,直径0.5 mm,弹性模量为206 GPa,泊松比为0.3,密度为7 900 kg/m3。
在钢化真空玻璃抽真空后(小于10-5Pa),玻璃板面外侧受到一个大气压(101 kPa)的作用,此时,采用Abaqus工程软件对钢化真空玻璃进行受力分析,玻璃上的应力云图如图2(b)所示。从图2(b)可以看出,钢化玻璃上受力最大位置集中在球形支撑处,其最大应力可达到24.87 MPa(小于90 MPa),玻璃处于弹性状态。
由于支撑物强度高、体积小,抽真空后支撑物与钢化玻璃的作用力较大,进而支撑物对钢化玻璃产生一定的压痕,即玻璃出现微损伤(见图3)。受钢化玻璃的品质和钢球作用力的影响,钢化玻璃上的压痕形态略有不同,但总体来说,在压力作用下钢球对钢化玻璃产生一个压应力区域,在接触圆的边缘产生一个拉应力区域,这种拉应力将会导致锥形断裂。同时,统计了50个压痕的扫描图,球体与玻璃接触的圆形直径约为0.193 7 mm,玻璃内部微损伤直径约为0.427 3 mm。
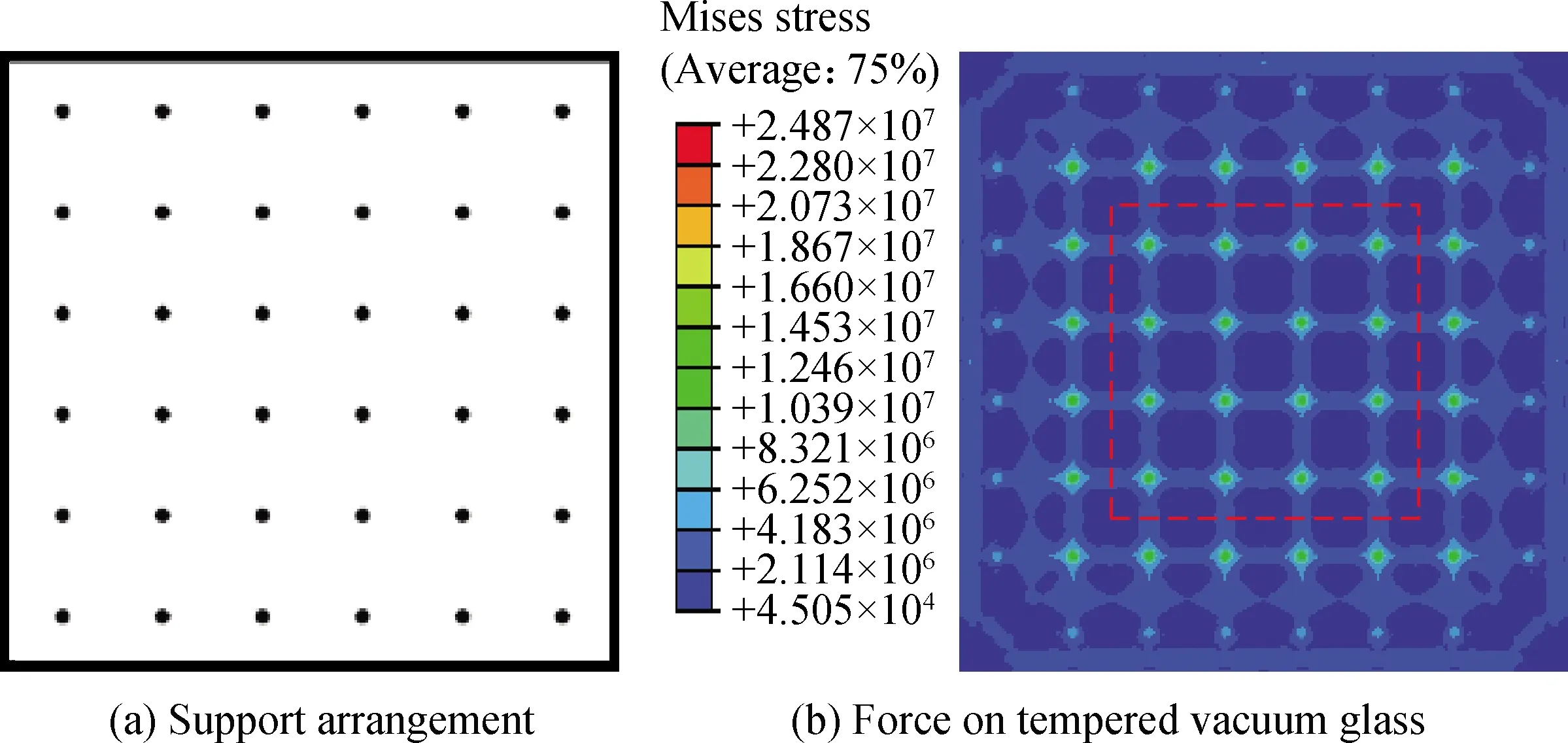
图2 钢化真空玻璃支撑物排布及受力图Fig.2 Arrangement and force diagram of tempered vacuum glass supports

图3 压痕扫描(部分)(a)200倍放大(b)3D扫描面(c)压痕变形曲线Fig.3 Indentation scanning (part) (a) 200 times magnification (b) 3D scanning surface (c) indentation deformation curves
2 玻璃受力应力场理论
假设钢化玻璃(半无限大)的杨氏模量为E,泊松比为ν;球形支撑物半径r0,杨氏模量为E0,泊松比为ν0。当球形支撑物以法向力F作用在玻璃表面上时(见图4),采用赫兹接触力学表示的接触半径a为[14]:

图4 赫兹压痕示意图Fig.4 Hertz indentation schematic diagram
(1)
式中:k为无量纲系数。
(2)
在此,采用简化柱坐标,并令R=r/a和Z=z/a,r为玻璃内距z轴的距离,z为玻璃受压面到玻璃内的距离。用隐式方程定义量L为:
(3)
因为L≥0,因此可以解出:
(4)
利用上述关系,可得柱坐标下的全应力场为:
2006年,我考入中央戏剧学院编导专业。毕业后,我留在北京,交了一个男朋友,他叫周磊,也是个编剧。妈妈专门来了一趟北京见周磊,周磊做了一桌饭菜,虽然谈不上多好吃,但那份用心和诚意,却让妈妈对他非常满意。
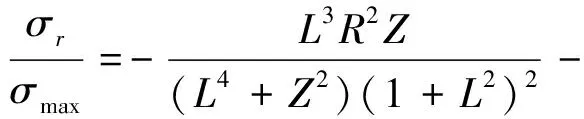
(5)
(6)
(7)
(8)
(9)
基于此,主正应力和最大主剪应力可表示为:
(10)
σ2=σθ
(11)
(12)
(13)
锥形裂纹沿着与最大主拉应力σ1正交的线传播,因此沿着以σ2和σ3应力轨迹与表面夹角α为特征的面传播,即:
(14)
式中:σr为径向应力;σθ为环向应力;σmax为最大应力;σz为轴向应力;τzr为轴向剪应力;τrθ为径向剪应力;τzθ为环向剪应力;σ1、σ2、σ3分别为第1,2,3主应力;τ13为最大主剪应力。
3 玻璃应力场计算结果与分析
对于尺寸为400 mm×400 mm的钢化真空玻璃,因为玻璃边部支撑受封接焊料影响,为了描述支撑物对玻璃的力学性能,取中部位置受边部影响较小的区域(200 mm×200 mm,见图2(b)),在大气压作用下,每个支撑物上所受力大约为250 N。采用式(1)和式(2)及支撑物和钢化玻璃的参数,计算可得到接触圆面直径2a为0.199 0 mm,与图3(a)中内圆(玻璃接触圆面)直径的平均值0.193 7 mm基本一致。
根据上述推导的应力场分布方程,采用Matlab对上述方程进行数值计算,进而获得应力的变化及应力场分布,如图5所示,这是典型的脆性材料应力变化图。从图5(a)可以看出,在接触区域内,除了非常接近接触边缘处,所有的主应力都是压应力,而且σ1>σ2>σ3;在接触区域之外,σ3= 0,σ1成为拉应力,但σ2仍然是压应力。径向应力σ1是裂纹萌生的主要原因,而环向应力σ2是导致玻璃形成环形裂纹的主要原因。同时,从图5(b)可以看出,在表面处,σr和σz达到最大,而剪切应力τ13在压痕正下方某位置达到最大。

图5 玻璃表面应力变化Fig.5 Changes in surface stress of glass
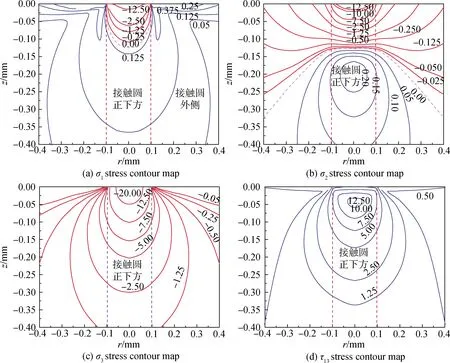
图6 主应力的等值线图Fig.6 Contour map of principal stress
在包含加载轴的平面上,主应力的轮廓如图6所示。在玻璃表面挤压的正下方,有一个水滴状的区域,在这个区域内所有的主应力都表现为压应力。在这个区域之外,σ1变成了拉应力,而其他应力仍然是压应力。然而,σ2在直接接触区域下方z=0.130 7 mm(即z/a=1.3处)也转变为拉应力。此外,σ3处为压应力,在接近表面的区域,它的方向朝着非常接近径向变化。
与Mouginot等[15]所给的算法及结果相比,虽然算法的一般形式是相似的,但应力等值线的大小实质上是不同的。表面处和表面以下的拉应力变化情况可以总结为:(1)拉应力在接触边缘处达到最大,在玻璃表面沿接触边缘径向距离增大,拉应力下降相对缓慢;(2)拉应力随着玻璃表面以下深度的增加而迅速减小;(3)最小主应力的轨迹开始与玻璃表面正交,并迅速从接触边缘向外偏离,形成一系列近似平行的曲线,这些曲线紧密地再现了锥形裂纹的形状。最大拉应力总是垂直于这些轨迹。因此,在最大主拉应力σ1的作用下,可以合理地假设圆球加载后裂纹遵循最小主应力σ3的轨迹。在本文研究中,方程(13)给出了最大主应力轨迹与玻璃表面之间的夹角,对于玻璃泊松比v=0.2,与玻璃受压面的夹角α=35°。
4 断裂韧性
(15)
长度为2c0的内裂纹在法向应力σ1(c)作用下的应力强度因子为:
(16)
在此,采用归一化应力强度因子,即:
(17)
式中:σij为裂纹尖端应力;fij为与环向角度θ相关的函数;c为裂纹长度;c0为内裂纹长度(图3);K和K0为应力强度因子,K0=σ0a1/2;由于σ0是压痕载荷和接触面积半径的函数,而接触面积半径a也是压痕载荷的函数,K0只是压痕载荷的函数。这意味着式(17)给出了一系列随着压痕载荷变化的曲线。
当考虑锥形裂纹在建立的应力场作用下的扩展时,将作出以下假设:(1)存在的裂纹不干扰应力场;(2)赫兹锥裂纹的形成来源于最大主拉应力σ1,且该应力始终垂直于裂纹路径;(3)初始向下裂纹相对于整个锥裂纹长度较小,可以忽略不计。可以用式(17)计算给定归一化裂纹长度c0/a和压痕载荷F时的应力强度因子。
对式(17)进行数值求解,可表示为:
(18)
式中:c* (19) 图7 不同压痕载荷下归一化强度因子Fig.7 Normalized strength factor under different indentation loads 采用式(18)计算不同载荷下归一化圆锥裂纹路径处的归一化应力强度因子其结果如图7所示。 图7表明了从现有环形裂纹发展成锥形裂纹,曲线表示计算的应力强度在圆锥裂纹尖端的长度增加。对于已知的圆锥裂纹长度,在给定的压痕载荷F作用下,可以求出临界应力强度。随着裂纹的扩展,应力强度因子减小,在离表面一定距离后,应力强度因子达到临界值,裂纹停止。因此,裂纹尖端的应力强度因子决定了断裂韧性。由于式(17)中的归一化因子K0仅与压痕载荷F有关,不同载荷下的归一化应力强度因子曲线形状相同,但会发生偏移。然而,在不同的载荷作用下,裂纹尖端的应力强度因子是恒定的。 (1)在压力作用下钢球对钢化玻璃产生一个压应力区域,在接触圆的边缘产生一个拉应力区域,这种拉应力将会导致锥形断裂。 (2)在接触区域内,所有的主应力都是压应力,而在接触区域之外,第1主应力σ1变为拉应力,第2主应力σ2仍然是压应力。第1主应力是裂纹萌生的主要原因,第2主应力是导致玻璃形成环形裂纹的主要原因。 (3)在最大主拉应力的作用下,圆球加载后裂纹遵循最小主应力的轨迹。 (4)不同压痕载荷下的归一化应力强度因子曲线形状相似,但有偏移,表明临界应力强度因子与压痕载荷和裂纹尺寸无关。因此,赫兹压痕法可以直接用来估算断裂韧性。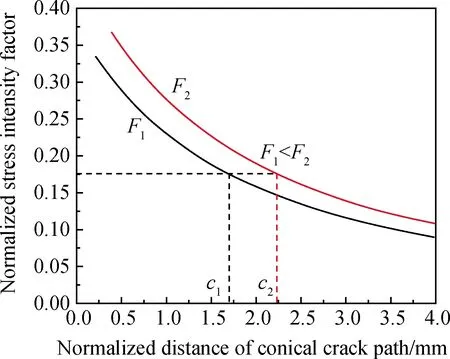

5 结 论
