分支定价割平面法求解带时间窗和人力分配的车辆路径问题

苏欣欣，伊廷刚，秦 虎

分支定价割平面法求解带时间窗和人力分配的车辆路径问题

苏欣欣1，伊廷刚2，秦 虎1

(1. 华中科技大学，管理学院，武汉 430074；2. 联勤保障部队供应局，武汉 430000)

本文研究了带时间窗和人力分配的车辆路径问题，并提出用分支定价割平面法来求其最优解。分支定价割平面法首先根据Dantzig-Wolfe分解技术将问题的数学模型分解为基于路径的主问题模型和求最短路径的子问题模型，然后利用列生成和标签算法在主问题和子问题之间进行迭代，并使用割平面法调整可行区域来求得主问题的最优松弛解，最后采用基于车辆数目和弧的分支策略获取原问题的整数解。算法中加入了两种加速策略：双向标签算法和递减搜索空间法。通过对多组算例进行测试，验证了模型和算法的准确性，并分析了患者数目和车辆数目对结果的影响，也说明了割平面法具有提高算法效率的作用。最后，对大规模算例进行测试的结果也为实际应用提供了理论依据。

车辆路径问题；人力分配；分支定价割平面法；救护车；列生成

0 引 言

随着我国社会经济的快速发展，人们对自身健康的关注意识逐渐提高，尤其对医疗救助方面的相关服务提出了更高的质量要求。人力和救护车是维持医院正常运转的重要医疗资源，合理调度人力和救护车不仅是满足患者健康需求的重要因素，更是提高院前服务水平的关键。

医院调动救护车一般有两种情况：紧急救助和非紧急救助。在紧急救助的情况下，急救中心需要根据病人病情的危急程度和地理位置做出应急响应，安排救护车和相关医疗人员进行争分夺秒的抢救，保障人民群众的健康与生命。此情况大多数出现于重大突发性事故和自然灾害中，并已有相当多的学者对此类问题进行了广泛的研究，可参考文献[1-3]。在非紧急救助的情况下，救护车的主要作用是有效地转移位于不同地理位置的患者到医院。有些患者由于年老或伤痛的原因无法独自前往医院而需要家属陪同，因此救护车不但要转移患者，还要一同转移其陪同家属。甚至有些受伤的病人需要轮椅或者担架的辅助才能移动，救护车上必须配备除了司机之外的辅助人员帮助患者操作轮椅或者担架。至此，在医院提供非紧急救助转移服务并且患者有转移时间窗需求的背景下，本文将研究带时间窗和人力分配的车辆路径问题(Manpower Allocation and Vehicle Routing Problem with Time Windows，MAVRPTW)。

MAVRPTW在带时间窗的车辆路径问题基础上，增加了每辆车的人员分配。为了尽可能地转移所有患者，医院需要同时考虑以下两个问题：① 在每辆救护车上配备若干名辅助人员；② 为每一辆救护车设计行驶路线。在MAVRPTW问题中，救护车和辅助人员从医院出发接受患者的转移请求，最终返回医院。此问题要求满足以下条件：(1)患者及其陪同家属要一同被接送至医院；(2)患者的转移时间必须在患者要求的时间窗之内。(3)救护车配备的辅助人员数目必须满足车上每一位患者的需求；(4)救护车上的总人数不能超过车辆的载人限制。由于救护车的数目有限，存在一些患者未能被转移而需要被外包给其他团队，因此会产生额外费用。MAVRPTW问题的目标是使得医院完成所有患者转移的总费用最少，包括未完成转移请求的外包费用、雇佣辅助人员的费用和车辆总行程的费用。

MAVRPTW问题的示例如图1所示，假设车辆的载人限制=12。从图中可以直观地发现，患者1的转移人数为2，表示该患者需要1位家属陪同，同时该患者需要2位辅助人员。其他患者的转移需求同样可以在图中找到。需要指出的是一些细节在图中被省略了，因为它们无法说明这个示例的主要特点。路径1转移了3位患者，总转移人数为6，车上配备了2个辅助人员，因此该车辆一共载有8个人。由于患者5的转移时间窗无法满足，因此患者5不能被此车辆转移。路径2也转移了3位患者，并配备了3个辅助人员，车辆一共载有11个人。由于车辆的载人限制，患者5不能被车辆2转移，最终患者5只能被外包。

图1 MAVRPTW问题的示例

MAVRPTW既考虑到了人员的分配，又考虑到了车辆路线的设计。近年来，已有若干学者开始研究与MAVRPTW相关的问题。Kim某人[4]介绍了一种多阶段的带有人力团队调度的车辆路径问题。在这个问题中需要按照给定的顺序执行客户的多个任务，且每个任务由一组团队执行。他们提出了一种基于粒子群优化的启发式算法。2012年，Pureza等[5]首次提出了带有多个配送人员的车辆路径问题，并采用禁忌搜索算法和蚁群算法对该问题进行求解。Munari等[6]针对带有多个配送人员的车辆路径问题首次提出了分支定价割平面法求解该问题，实验结果证明了该算法具有一定优势并得到了文献中未知的上界。苏欣欣等人[7]在该问题的基础上，对某些约束和目标进行一定的改进，并设计了禁忌搜索算法处理该问题。Li等人[8]首次提出具有同步约束的人力路径问题，该问题的任务是安排一组拥有不同技能的工人一起完成一系列的工作。针对该问题，他们建立了数学模型，并提出了一种模拟退火算法来求解此问题。Luo等[9]提出了分支定价割平面法来求解具有同步约束的人力路径问题，与CPLEX进行对比，证明了分支定价割平面法具有求解更多算例最优解的能力。根据香港非紧急救护车转移患者的现象，2017年，Lim等人[10]提出了带有时间窗和人员排班的多程取送货的车辆路径问题。为求解决这个问题，他们提出了多循环的局部搜索元启发式算法，并在局部搜索过程中引入了变邻域下降法。随后，Zhang等[11]结合实际情况首次提出了带人力分配的车辆路径问题(Manpower Allocation and Vehicle Routing Problem，MAVRP)，并建立了对应的数学规划模型，最终采用若干变邻域搜索算法对此问题进行求解。

本文提出的MAVRPTW问题在Zhang等[11]的基础上，考虑了患者的转移时间窗需求。这虽然使得问题更加复杂，为医院安排救护车转移患者的服务提出了更高的要求，但是却给患者带来了便利，并进一步提升了院前服务水平。在求解算法方面，提出使用分支定价割平面法来得到MAVRPTW问题的最优解，并在该精确算法中加入两种加速策略：双向标签算法和递减搜索空间法。通过对多组算例进行测试，验证了本文所提出精确算法的高效性和准确性，并分析了相关参数对结果的影响，同时也证实了割平面法具有提高算法效率的作用，最后，对大规模算例进行测试的结果也为实际应用提供了理论依据。

1 数学模型

MAVRPTW是在车辆路径问题的基础上加入了人力分配问题，这会使得问题更加复杂。它不仅需要考虑车辆的路线和调度决策，还要决定每辆车分配的辅助人员数目。从数学模型的角度来看，带人力分配的模式会给问题带来更多的决策变量，也会使得原路径优化问题增加更多关于人力分配的复杂约束。为构建数学模型，定义相关参数如下：

决策变量如下：

根据上述参数，本文描述的问题可归结为如下数学模型：

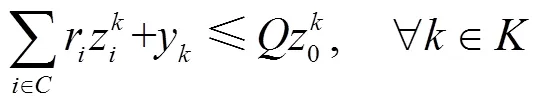
2 Dantzig-Wolfe分解

上述的数学模型中含有大量的约束和变量，这使得计算过程相当复杂。为了求得该问题的最优解，我们使用Dantzig-Wolfe分解技术将该数学模型分解为一个基于可行路径的Set Packing主问题和一个带资源限制的最短路径子问题。

2.1 Set Packing主问题模型

决策变量：

通过上述定义，可以将MAVRPTW问题的数学模型转化为下面的Set Packing模型，并称之为主问题(Master Problem，MP)：

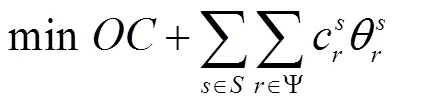
式中，式(14)表示最小化转移所有患者的总成本；式(15)表示每个点最多被转移一次；式(16)表示路径数目不能超过车辆总数目；式(17)表示变量属性。

2.2 子问题模型

3 分支定价割平面法

本文使用分支定价割平面法来求得主问题的最优整数解。其基本原理是利用列生成和标签法来搜索队列中节点的线性松弛最优解并在此过程中利用割平面法加入有效不等式提高松弛解的下界，并使用分支定界算法来对节点进行分支搜索。在搜索过程中，如果节点的下界大于等于全局上界，那么这个节点可以删除；如果节点的下界小于全局上界，解为整数时更新全局上界，解为分数时要根据分支策略进行分支。当队列为空或者全局下界等于全局上界时，算法终止。下面本文将详细描述算法的各个部分。

3.1 初始解的生成

本文采用贪婪算法生成初始解。假设车辆数目足够，算法最初使每一辆救护车对应一个空路径，随机分配辅助人员，然后循环将患者插入这些路径中的最优为止，保证插入该患者后路径的费用最少，直至没有患者可以插入到路径中为止，那么一个初始解完成，并将其作为树的根节点。

3.2 标签算法

为了提高算法的速度，使用占优准则来减少在标签算法中扩展的标签数量。在已有的标签中，占优准则可以确定一个子集，保证最优路径在这些占优标签中产生。不在子集中的标签，即被占优的标签，将会被丢弃，防止做无效扩展，从而加快算法速度。

3.3 递减搜索空间

递减搜索空间(decremental state-space relaxation)是由Boland等人[12]在2006首次提出的一种加快求解子问题速度的方法。在标签算法中，该方法首先将一个点只能被一条路径访问的条件进行松弛，即允许一个点被一条路径多次访问。在最终得到的路径中，若存在一个点被访问多次，则限制该点只能被路径访问一次，并重新对子问题进行求解，直至最终得到的路径中每一个点只被该路径访问一次为止。

3.4 割平面法

3.5 分支策略与整数解

4 实验结果及分析

4.1 算例说明

分支定价割平面法使用Java语言进行编写，并使用CPLEX(Studio1251)求解受限主问题。运行环境采用Intel(R)Core(TM)i7-4790 CPU @ 3.60GHz(8.00 GB内存)，且实验中的计算时间以秒为单位进行统计。

按照时间窗的紧凑程度和点的分布规律，Solomon测试算例被划分为6种类型。我们在每个类型中随机选择4个算例，因此本文中一共有24个标准测试算例。由于每一个标准测试算例包含100个患者，为了更全面、更充分地研究分支定价割平面法的性能，对每一个算例选取部分数据生成具有不同患者数目的测试算例，并定义含有0～20个患者的算例为小规模算例，含有20～50个患者的算例为中规模算例，含有50～100个患者的算例为大规模算例。

4.2 与CPLEX对比实验

为了验证分支定价割平面法的准确性，将其与CPLEX进行比较，并采用小规模算例进行测试。针对每一个标准算例，选择每一个算例的前11个点和前21个点，分别组成含有10个患者和20个患者的小规模算例。设置分支定价割平面算法和CPLEX运行每一个算例的时间限制为7 200s，且只运行一次。

表1 小规模算例求解结果(10个患者、2辆车)

20个患者、4辆车的小规模算例的求解结果如表2所示。从实验数据可知，在7 200s内，只有10个算例CPLEX能求得最优解。对比获得的最优解，分支定价割平面法的求解结果与之相同且求解时间远低于CPLEX的求解时间。对于CPLEX未能求出最优解的14个算例，分支定价割平面法均以很短的时间求出了最优解。实验结果说明了分支定价割平面法的正确性，并且相比CPLEX具有一定的效率。

表2 小规模算例求解结果(20个患者、4辆车)

4.3 灵敏度分析

由于患者数目和车辆数目直接影响分支定价割平面法的计算结果，因此本文将分析这两个参数的变化对计算结果的影响。

针对以上24个算例，使用中等规模的数据进行分析，患者数目选取30和40，车辆数目选取6、7和8。这样的取值不但使得测试算例具有代表性，而且能保证算法的求解效率。计算结果分别统计在表3和表4中。在这两个表中，斜体的数据表示算法由于超出内存仅能返回的最小上界。

实验结果表明，当患者数目一定时，增大车辆数目能够降低转移患者的总费用，同时也提高了问题的复杂度，使得算法的求解时间增长。当车辆数目一定时，患者数目的增长，增加了转移患者的总费用，同样也使得问题的求解难度增强。

表3 中规模算例求解结果(30个患者)

表4 中规模算例求解结果(40个患者)

4.4 割平面法的测试与分析

本文提出的精确算法是在分支定价的基础上加入了割平面法，从而达到提高松弛解下界，有效减少分支定界中分支的作用。为了验证割平面法的有效性，分别将分支定价割平面法和不包含割平面法的分支定价算法对大规模算例进行了测试。测试算例的规模为50个患者和15辆车，实验结果统计于表5中。

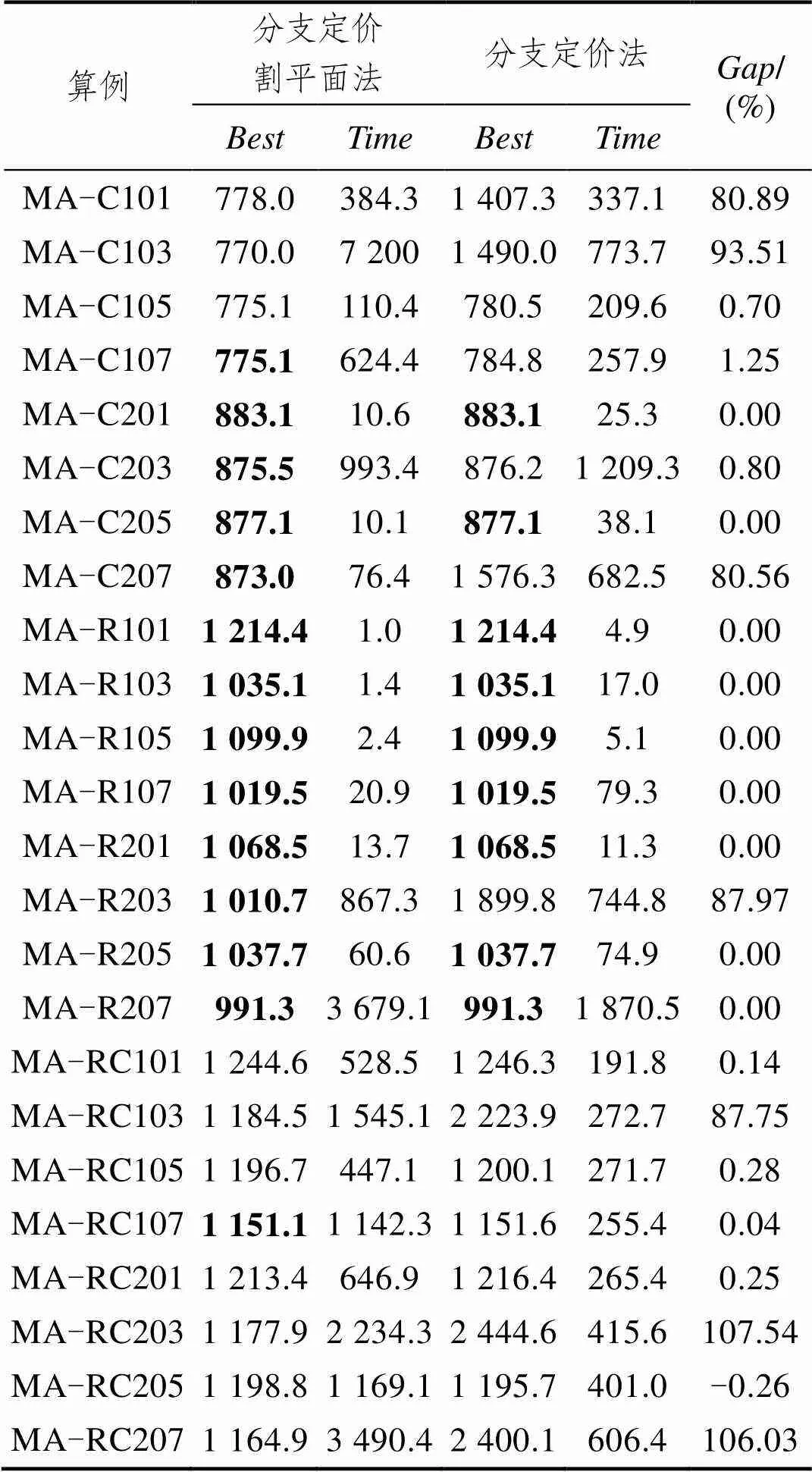
表5 大规模算例求解结果(50个患者、15辆车)

从表5中可以看出，在24个算例中分支定价割平面法可以得到14个最优解，而不包含割平面法的分支定价算法只能获得9个最优解。在两种算法均得到最优解的情况下，分支定价割平面法获得最优解的求解时间明显低于分支定价算法的求解时间，只有算例MA-R201和MA-R207的求解时间略高于分支定价算法的求解时间。对比两种算法得到的最小上界，分支定价割平面法得到的结果大部分低于分支定价算法得到的结果，只有算例MA-RC205分支定价割平面法得到的结果大于分支定价算法得到的结果，且相对误差仅为0.26%。从本质上分析，是由于割平面法能够优化主问题的数学模型，快速提高松弛解下界，使得算法可以对无效节点进行及早剪枝，从而达到节约大量存储空间和求解时间的作用。

4.5 分支定价割平面法求解规模的测试

为了研究分支定价割平面法能够求解的算例规模，本文对以上24个算例使用两种不同的大规模算例进行了测试，并将测试结果统计在图2中。从图2中可知，当患者数目为50、车辆数目为20时，71%的算例可以通过分支定价割平面法得到最优解；而当患者数目为70、车辆数目为25时，仅有42%的算例可以通过分支定价割平面法得到最优解。算例的患者数目和车辆数目是影响分支定价割平面法能否求解该算例的关键因素。在实际应用中，此测试结果也为使用分支定价割平面法求解MAVRPTW问题提供了一定的参考和依据。

图2 分支定价割平面法求解大规模算例的统计结果

5 结 论

本文研究了带时间窗和人力分配的车辆路径问题(MAVRPTW)，并使用分支定价割平面法求解此问题。分支定价割平面法首先根据Dantzig-Wolfe分解技术将问题的数学模型分解为基于路径的主问题模型和求最短路径的子问题模型，然后利用列生成和标签算法在主问题和子问题两者之间进行迭代，并使用割平面法调整可行区域来求得主问题的最优松弛解，最后采用基于车辆数目和弧的分支策略获取原问题的整数解。算法中加入了两种加速策略：双向标签算法和递减搜索空间法。通过对多组算例进行测试，证实了模型和算法的正确性，分析了患者数目和车辆数目对结果的影响，同时也说明了割平面法具有节约存储空间和提高算法效率的作用。最后，对大规模算例进行测试的结果也为实际应用提供了理论依据。

未来的研究中，在算法上，我们将探索精确算法与启发式算法进行结合，从而提高算法的计算效率。在问题模型上，我们将对MAVRPTW问题进行扩展，如同时考虑患者被转移和被送回的请求，从而提高医院的服务水平。

[1] 傅芳, 吴佩珊. 救护车智能化调度的现状分析与思考[J]. 电脑与电信, 2019: 8-9.

[2] 刘冠男, 曲金铭, 李小琳, 等. 基于深度强化学习的救护车动态重定位调度研究[J]. 管理科学学报, 2020, 23(2): 39-53.

[3] JEONG Y, JEONG H, KO J. Optimal decisions on the quantity and locations of. ambulances for the timely response to emergency requests[J]. Fire Science and Engineering, 2017, 31(3): 137-143.

[4] KIM B I, KOO J, PARK J. The combined manpower- vehicle routing problem for multi-staged services[J]. Expert systems with Applications, 2010, 37(12): 8424-8431.

[5] PUREZA V, MORABITO R, REIMANN M. Vehicle routing with multiple deliverymen: Modeling and heuristic approaches for the VRPTW[J]. European Journal of Operational Research, 2012, 218(3): 636-647.

[6] MUNARI P, MORABITO R. A branch-price-and-cut algorithm for the vehicle routing problem with time windows and multiple deliverymen[J]. Top, 2018, 26(3): 437-464.

[7] 苏欣欣, 秦虎, 王恺. 禁忌搜索算法求解带时间窗和多配送人员的车辆路径问题[J]. 重庆师范大学学报(自然科学版), 2020, 37(1): 20-30.

[8] LI Y, LIM A, RODRIGUES B. Manpower allocation with time windows and job-teaming. constraints[J]. Naval Research Logistics (NRL), 2005, 52(4): 302-311.

[9] LUO Z, QIN H, ZHU W, et al. Branch-and-price-and-cut for the manpower routing. problem with synchronization constraints[J]. Naval Research Logistics (NRL), 2016, 63(2): 138-171.

[10] LIM A, ZHANG Z, QIN H. Pickup and delivery service with manpower planning in Hong Kong public hospitals[J]. Transportation Science, 2017, 51(2): 688-705.

[11] ZHANG Z, QIN H, WANG K, et al. Manpower allocation and vehicle routing problem in non-emergency ambulance transfer service[J]. Transportation research part E: logistics and transportation review, 2017, 106: 45-59.

[12] BOLAND N, DETHRIDGE J, Dumitrescu I. Accelerated label setting algorithms for the elementary resource constrained shortest path problem[J]. Operations Research Letters, 2006, 34(1): 58-68.

[13] JEPSEN M, PETERSEN B, Spoorendonk S, et al. Subset- row inequalities applied to the vehicle-routing problem with time windows[J]. Operations Research, 2008, 56(2): 497-511.

[14] DESAULNIERS G, DESROSIERS J, Solomon M M, et al. A unified framework for deterministic time constrained vehicle routing and crew scheduling problems[M]. Boston, Fleet management and logistics. Springer, 1998: 57-93.

[15] SOLOMON M M. Algorithms for the vehicle routing and scheduling problems with time window constraints[J]. Operations Research, 1987, 35(2): 254-265.

Branch-and-Price-and-Cut Algorithm for the Manpower Allocation and Vehicle Routing Problem with Time Windows

SU Xin-xin1, YI Ting-gang2, QIN Hu1

(1. School of Management, Huazhong University of Science and Technology, Wuhan 430074, China; 2. Joint Support Force Supply Bureau, Wuhan 430000, China)

This paper studies the manpower allocation and vehicle routing problem with time windows (MAVRPTW) and proposes a branch-and-price-and-cut algorithm to obtain its optimal solution. The algorithm first decomposes the mathematical model of the original problem into a master model based on routes and a subproblem model for the shortest path problem according to the Dantzig-Wolfe decomposition. It then employs a column generation method and a label-setting algorithm to calculate between the master problem and the subproblems iteratively. Moreover, subset-row cuts are generated to adjust the feasible region during these processes. Finally, by obtaining the optimal solution to the linear relaxation of the main problem, the algorithm adopts branching strategies based on the vehicle number and arc for the integer solutions of the problem. In order to improve the efficiency of the algorithm, we use two accelerating strategies: a bidirectional label-setting algorithm and a decremental state-space relaxation. Comparisons with CPLEX show that the algorithm performs well in terms of stability and efficiency. By carrying out extensive computational experiments, we not only analyze the influence of the number of patients and vehicles on the results, but also find that the cutting plane method is capable of improving the efficiency of the algorithm. Finally, test results of large-scale instances provide a theoretical basis for practical application.

vehicle routing problem; manpower allocation; branch-and-price-and-cut algorithm; ambulance; column generation

U116.2

A

10.19961/j.cnki.1672-4747.2021.04.016

1672-4747(2021)04-0075-12

2021-04-14

2021-05-29

2021-06-02

2021-04-14～04-21； 05-28～05-29

国家自然科学基金创新研究群体项目(71821001)；国家自然科学基金面上项目(71971090)；国家自然科学基金面上项目(71571077)

苏欣欣(1991—)，女，汉族，博士，研究方向为车辆路径优化，E-mail：D201577825@hust.edu.cn

秦虎(1980—)，男，汉族，湖北武汉人，教授，研究方向为车辆路径优化，E-mail：tigerqin@hust.edu.cn

苏欣欣，伊廷刚，秦虎. 分支定价割平面法求解带时间窗和人力分配的车辆路径问题[J]. 交通运输工程与信息学报，2021, 19(4): 75-86.

SU Xin-xin, YI Ting-gang, QIN Hu. Branch-and-Price-and-Cut Algorithm for the Manpower Allocation and Vehicle Routing Problem with Time Windows[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 75-86.

(责任编辑：刘娉婷)