混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划

祁宏生，应雨燕，林俊山，姚志洪

混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划

祁宏生1，应雨燕1，林俊山2，姚志洪3

(1. 浙江大学，智能交通研究所，杭州 310058；2. 海南省热带汽车试验有限公司，海南琼海 571400；3. 西南交通大学，交通运输与物流学院，成都 611756)

为解决城市道路拥挤状态下车辆可行换道间隙少、换道时间长，进而导致停车等待、堵塞后续车流等问题，本文基于智能网联环境下车辆之间的交互协同，提出了一种混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划模型。首先，采用多项式和三角函数分别描述了换道过程中的空间轨迹和速度曲线，得出了换道间隙可行性判别依据。在此基础上，构造了换道启动可行状态集合，并构建了单个换道请求下的间隙适配和协同换道的最优控制模型。然后，考虑多换道需求，构建了主动间隙适配和换道序列规划模型，对换道序列进行整体优化。最后，设计了数值仿真实验，验证了本文模型可对多换道需求进行时空优化。仿真实验结果表明，本文模型能够降低换道行为对城市道路通行能力的影响，且适用于不同的交通需求，模型可提升24%的道路通过量。

智能交通；智能网联车辆；换道；轨迹规划；间隙；仿真

0 引 言

传统交通流理论分别采用跟驰模型和换道模型描述车辆的纵向和横向运动。车辆行驶过程中，驾驶员根据自身的期望速度和周边车辆的信息(位置、速度等)进行跟驰或换道的选择。相比跟驰行为，换道行为流程更为繁琐，对周围车辆的运行轨迹影响更显著，其研究意义更明显。传统换道模型未考虑车辆之间的信息交互和动作协同，因此更容易导致交通拥堵的形成和道路通行能力的损失。近年来，智能网联汽车的发展为交通管理与控制提供了新的机遇。智能网联汽车可通过车载传感器、控制器以及执行器等实现车辆间的信息交互，完成复杂的协同换道行为。但考虑到相关道路基础设施和汽车的升级换代需要一定的周期，因此，未来在相当长的一段时期内，道路上交通流将普遍由人工驾驶车辆(Human Driven Vehicles，HDV)和智能网联汽车(ConnectedAutomated Vehicle，CAV)构成。因此，研究混合交通流环境下，车辆之间的协同换道行为将更具有实际应用意义。

图1 间隙适配和协同换道

综上，本文面向混合自动驾驶车流场景，同时考虑有多个CAV换道需求，建立车-车协同的主动间隙适配和换道序列规划模型。首先，对换道行为建模及轨迹规划相关研究进行了回顾；然后，构建了混合自动驾驶场景下的多车主动间隙适配和换道序列规划模型；接着，设计了数值仿真实验，验证了本文模型的有效性；最后，为相关结论和对未来的研究展望。

1 文献综述

换道行为是自动驾驶车辆的基本任务，也是微观交通流模型的核心建模对象之一。一般而言，换道行为按动机可分为强制型换道和任意型换道[1]。任意型换道的目标是追求更快的速度，强制型换道的目标是进入目标车道，以完成特定驾驶目标(例如转向、驶离高速等)。当周围没有环境车辆时，换道车辆可按照自己的意愿进行自由换道；当周围存在环境车辆，换道行为受到环境车辆的影响。这种情况下，换道可分为强迫换道和协作换道。强迫换道是指换道时，车辆对周围其他车辆产生较大的干扰；协作换道则为目标车道的车辆主动减速，为换道车辆制造间隙。为了刻画上述驾驶员的换道行为和换道过程，相关学者做了大量的研究工作，Gipps[2]提出了基于规则的决策树结构换道模型；Yang和Koutsopoulos[3]提出了Gipps模型改进版，该模型增加了驾驶员的换道概率，并将换道过程分为意图生成、目标车道选择、间隙搜索和换道执行四个阶段；Zheng等[4]研究了换道行为对交通流的影响；Hidas[5, 6]提出了适用于城市道路和高速公路的换道模型；Kesting[7]基于安全规则和期望规则，提出了MOBIL换道模型；Ahmed等[8]提出了机遇离散选择换道模型；Toledo[9]将任意型换道和强制型换道统一考虑，构建了换道的效用模型，该模型考虑了保持在本车道和进入更快侧向车道的权衡。上述研究均基于人类驾驶员换道行为机理，为揭示交通流现象提供了诸多分析工具和视角。

随着智能网联汽车的发展，车辆不仅可以通过感知设备[10]获取车身周边的环境信息，还可以通过通信设备进行信息的交互[11]，从而完成各种复杂的驾驶行为。因此，在该环境下，CAV可对换道进行规划与执行。现有研究表明，CAV的换道轨迹模型有多种，常见的有多项式[12-16]、样条曲线[17]、三角函数[18]、贝塞尔曲线[19]Akçelik加速度曲线[20]等。柏海舰等[21]提出了无人车换道模型，其调整自身的速度至目标车道速度后再进行换道；黄玲[22]和兰凤崇等[23]提出了基于LSTM神经网络的换道模型，并利用NGSIM的数据进行了拟合分析；Do等[12]在日本高速路场景下对驾驶员的换道行为进行了研究，提出了拟人驾驶的两阶段换道模型。上述研究主要研究单个自动驾驶车辆的换道行为。在换道规划过程中，关键参数(例如换道持续时长)为先验固定值[12, 24]，这与实际不符，进而约束了换道轨迹的可行空间。根据实际观测和统计，不同驾驶员、不同场景中的换道行为表现出不同的参数特征，例如Sun[25]的观测结论为自由换道持续时长处于1.5s到3.5s之间，而协作换道则处于2s到6.5s。Hill[26]和Yang等[27]的观测结果也验证了换道持续时长的差异性。因此，上述研究针对智能网联环境换道模型的假设比较理想，且对周围环境车辆的信息考虑较少。

在高密度车流中，CAV可以与其他车辆交互实现协作换道。这种协作可体现于信息预测[28]、行为规划或优化[29]等。由于HDV不受控，当CAV的预期轨迹受到HDV影响时，只能中断换道过程[30]，此时，并未实现换道。在拥堵场景下，由于可行间隙变少，车辆换道成功性大幅降低。因此仅仅依靠CAV的单车智能，无法达成顺利换道目标。多CAV车辆之间的协同为顺利换道提供了可行条件，这种场景下存在两种CAV：换道需求CAV和间隙适配CAV。前者存在换道需求，后者通过减速、增大间隙，为前者提供换道机会。由于换道间隙位置、换道间隙大小、换道启动时刻、换道启动位置都为变量，现有的换道轨迹规划、可行性判据无法满足这种需求。当多个换道需求同时存在时，这一问题将更加复杂。上述分析表明，多换道需求场景下间隙适配和换道过程的规划尚无较好的解决方案。

为了解决上述缺陷，本文将拥堵混合自动驾驶车流场景下CAV的换道归纳为主动间隙适配和协同规划问题，并提出基于最优控制的成对CAV规划和换道序列优化模型。仿真结果显示，本文模型不仅能够规划多换道需求下的轨迹，还可降低换道行为对道路通行能力的影响。

2 主动间隙适配和换道序列规划模型

2.1 问题描述与模型框架

本文建模场景为城市干道上游可合法变道部分，如图2所示。

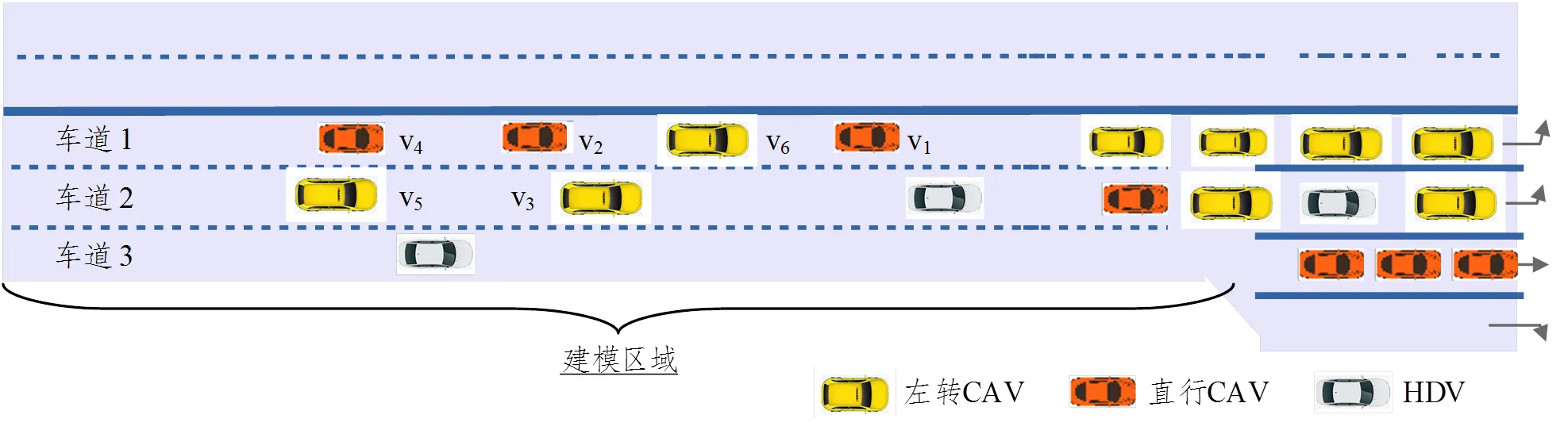
图2 建模区域

为便于建模，本文进行了相关假设：

假设1 智能网联车辆可获取该路段所有车辆的信息，包括其他智能网联车和人工驾驶车辆。人工驾驶车辆的信息可由CAV的车载检测器检测，也可通过路侧单元获取并传输到智能网联车辆。

假设2 对于人工驾驶车辆，本文采用智能驾驶员模型(Intelligent Diver Model，IDM)描述其跟驰行为。

假设3 CAV可实时判断目标车道间隙的可行性。优化结果的执行过程中，若HDV的行为导致目标车道的目标间隙过小从而无法实现换道，则换道规划算法重新运行。因此，本文将HDV的行为作为外界不可控因素，只要规划的轨迹和间隙使得换道不可行，则算法重新进行优化。

其中，假设2中的跟驰模型也可用其他跟驰模型进行替换，不影响本文所提出方法的整体框架。存在换道需求的CAV称之为换道需求车辆或换道需求车辆集。相互之间存在间隙适配可能的需求车辆称之为一个换道车辆群，例如，图3中存在车群A和车群B。车群A中存在换道需求的车辆为c3，车群B中存在换道需求的车辆为c6和c7。车辆c9需要换道，换道行为受到c10的影响，但是由于c10不是智能网联车，所以c9的换道决策假定c10的行为给定且不受控，因此，c9和c10不构成车群。同时，换道车群A和B的行为之间没有相互作用，可对这两个车群分别进行换道规划，无需考虑它们之间的相互影响。确定换道群的启发式方法在2.4节描述。

一个换道优化车群的换道行为需要协同考虑，例如，图3中车辆c3需要换道至直行车道，若c1决定减速为c3制造可行换道间隙，则c2无需为c3制造可行间隙。因此，对于一个换道优化群，需要考虑所有换道请求和间隙适配，进而得出最优决策。本文提出方法的整体工作流程如图4所示。

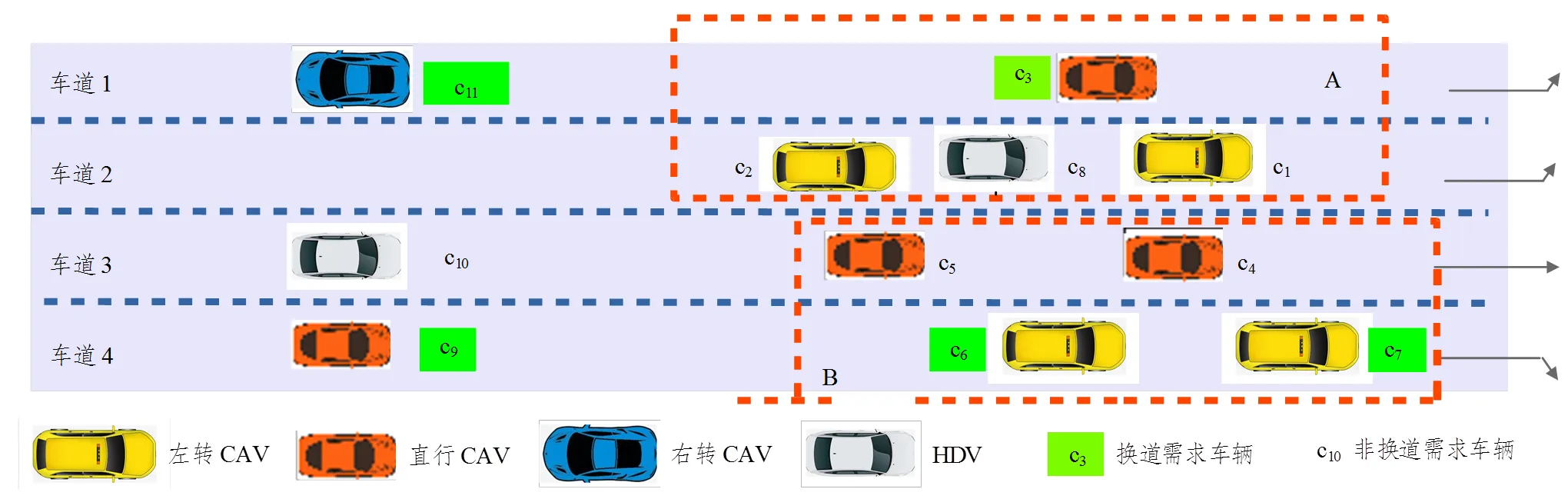
图3 换道需求车辆集及换道车群

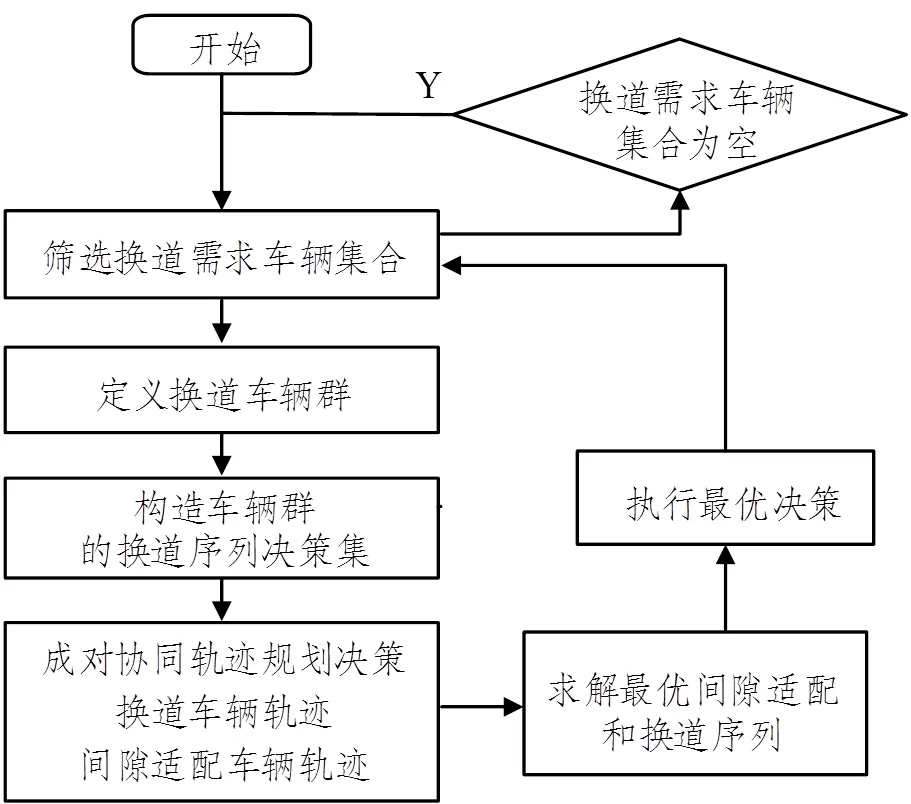
图4 模型工作流程图

(1)筛选换道需求车辆集合，该集合取决于车辆的转向需求和所在车道。

(2)定义换道车辆群，是指空间上相互接近，且需要进行换道协同的车辆集合，实际操作中可设定距离阈值确定。“成对协同轨迹规划决策”模块中，“成对”是指换道需求车辆和适应换道需求，进行加减速主动制造可行间隙的车辆。

(3)求解最优间隙适配和换道序列。当换道车辆群中存在多个换道请求，多个换道请求的执行顺序可以有不同的方案。满足所有换道需求的可行决策构成一个序列。本文从所有序列中选择执行时间最短者作为优化结果。

2.2 换道时空轨迹建模与可行性判据

CAV的换道过程可由车辆的时空轨迹来体现。在进行换道之前，需要寻找间隙、判断CAV能否利用该间隙安全完成换道。换道轨迹模型为根据相关条件(本车速度和位置、周围车辆速度和位置、车道宽度、道路限速)生成预期的行驶轨迹；换道可行性判据则为根据相关条件，判断车辆能否安全完成换道。

2.2.1 换道时空轨迹模型

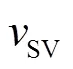
本文将空间轨迹和速度曲线进行解耦，分别建模：(1)如果轨迹中含有时间，则需要预先给出换道持续时长。根据观测，该值散布于一个区间内，同时，给定换道持续时长取值会压缩换道轨迹的可行解空间，因此不宜预先确定换道时长。(2)间隙适配过程中，SV车辆加速部分末端状态(也即图7的时刻的状态)对应的侧向车道间隙是否可行并不确定。因此，需要将末端状态的换道间隙可行性纳入优化问题的约束，该问题本质上是换道启动时刻可行状态集合的确定。

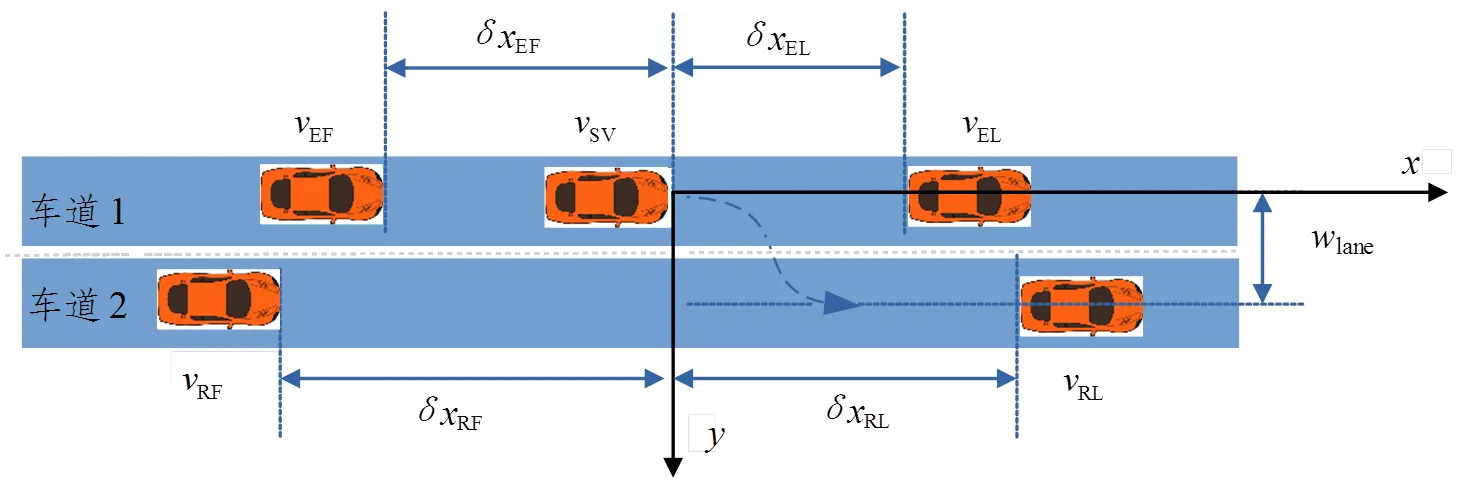
图5 换道场景

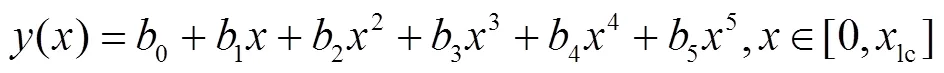
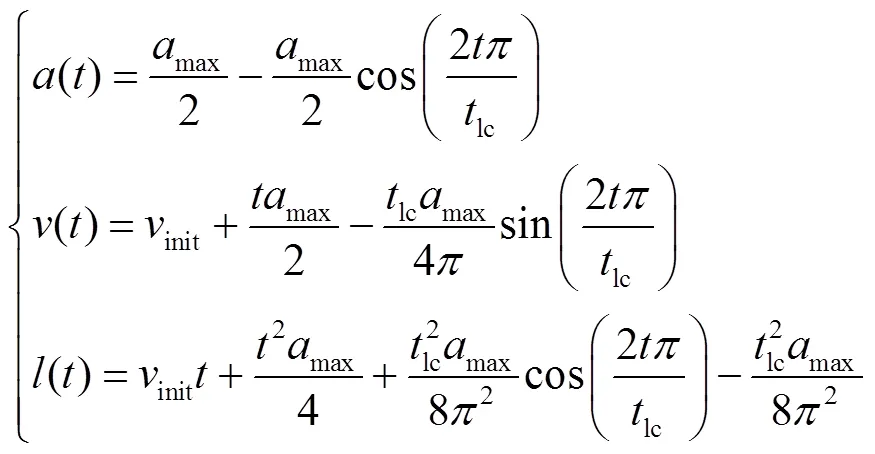
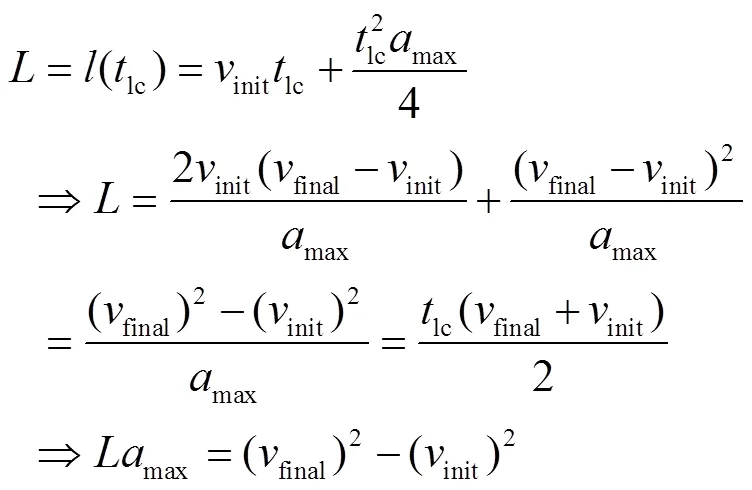
其中，加速度曲线、速度曲线和距离曲线中的参数满足如下约束：

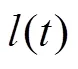
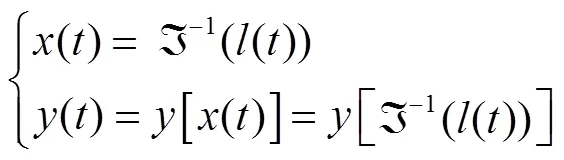
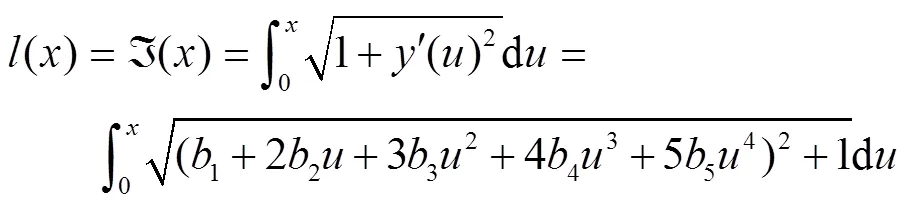
2.2.2 换道可行性判别

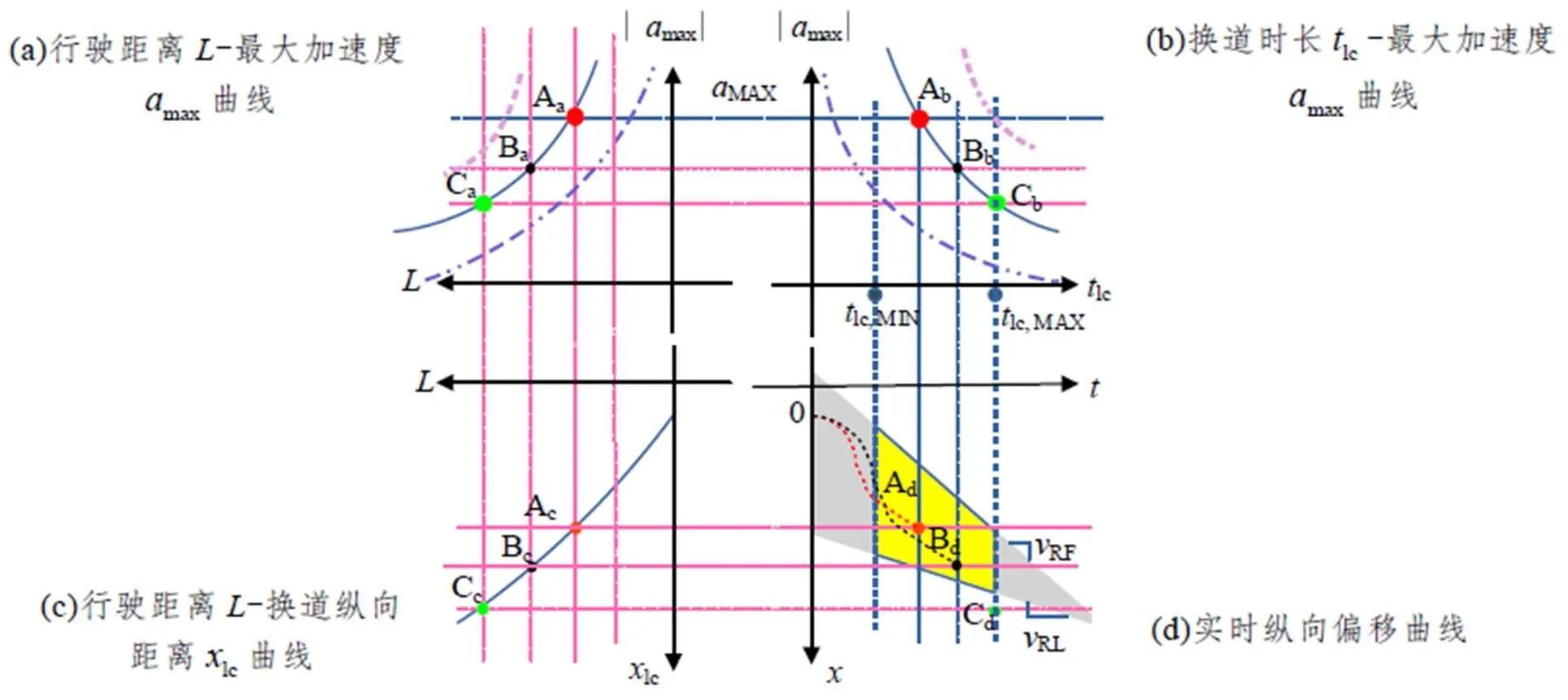
图6 换道可行性判据

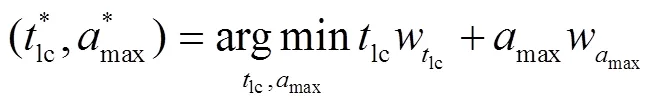
综上所述，换道可行决策和轨迹规划的流程为：

(5)判断是否满足本车道前车和后车、侧向前车和后车的安全要求；

(6)输出换道可行性判据结果(可行或者不可行)。

2.3 间隙适配和换道协同优化模型

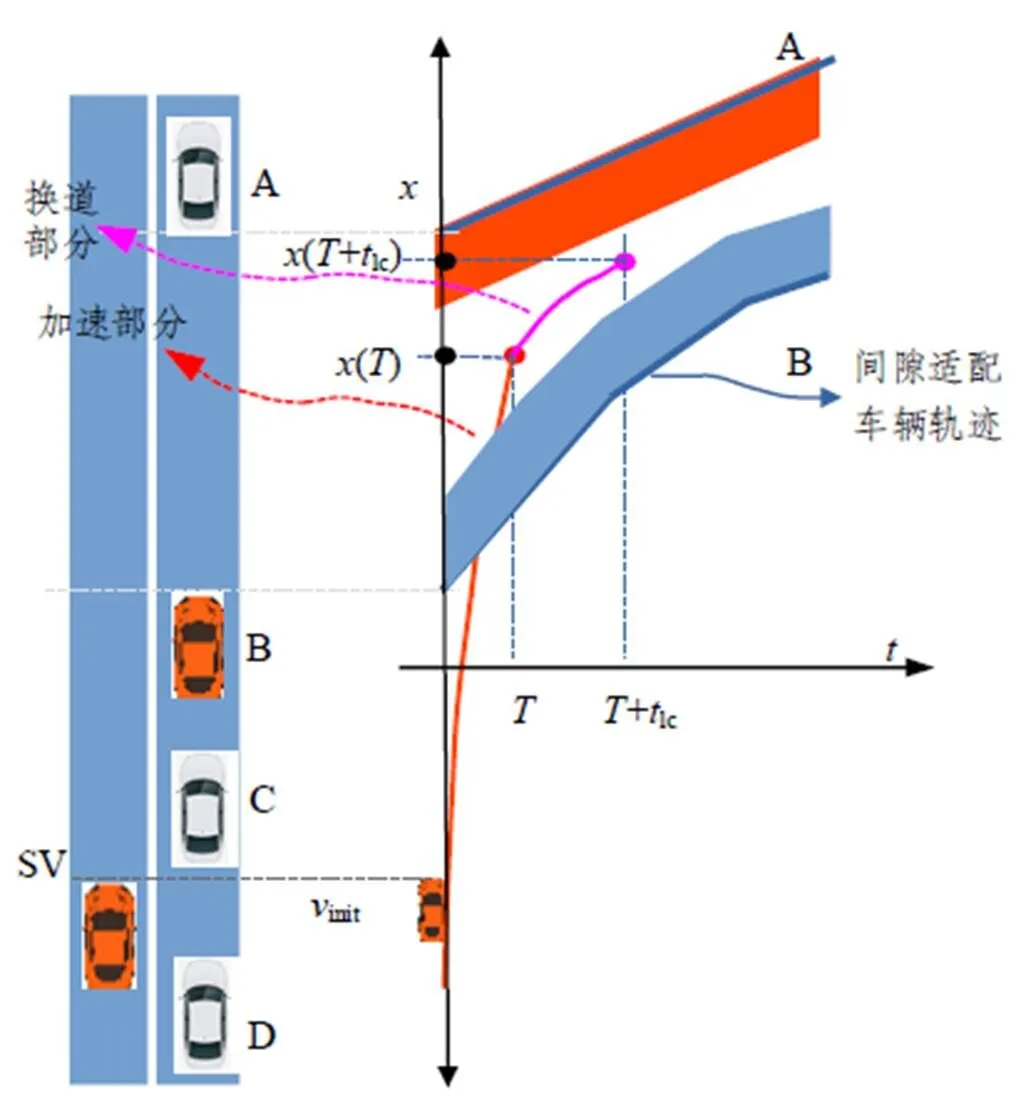
图7 间隙适配和换道协同优化

2.3.1 换道启动时刻可行状态集合确定

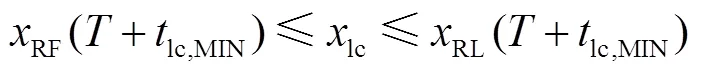
从而可得：

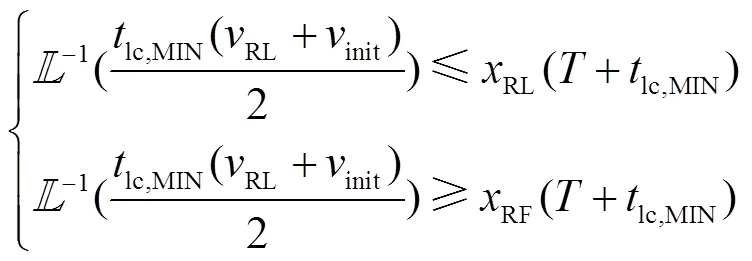
进一步，可得：

最终，得到：

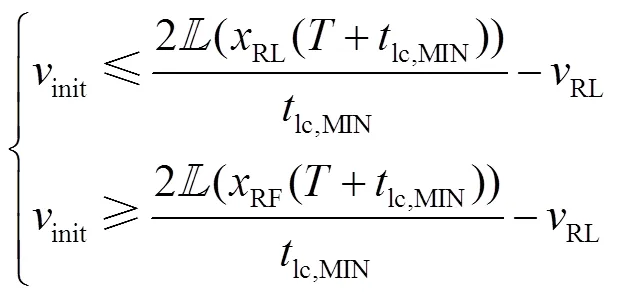
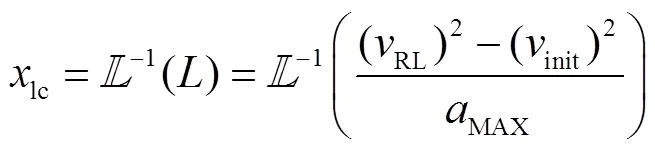
同理，依据式(11)得到式(16)。此外，考虑两种子情况：

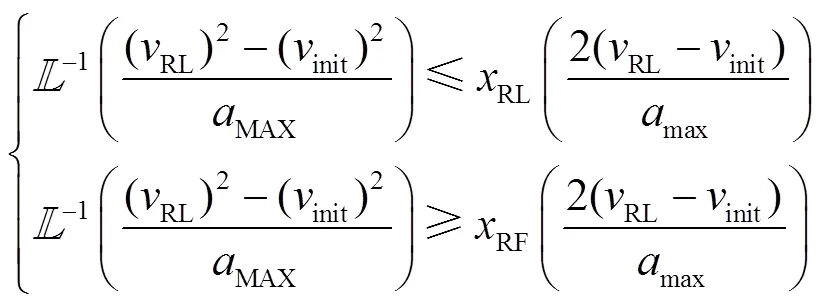
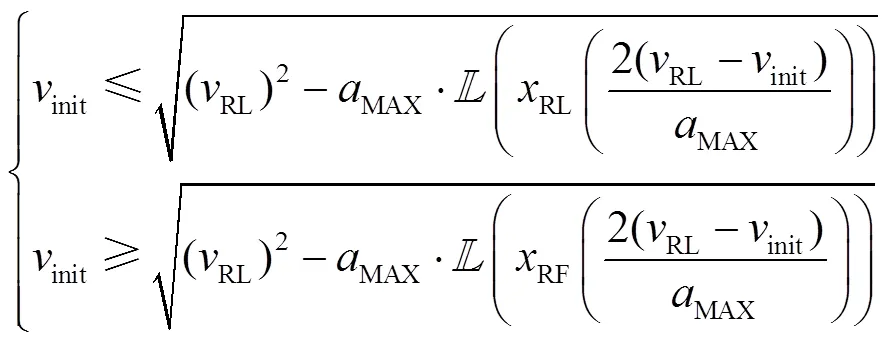
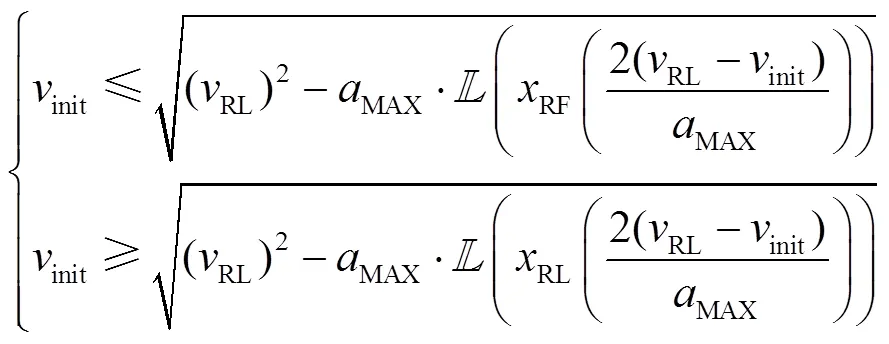
2.3.2 协同轨迹优化模型及求解

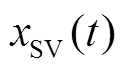
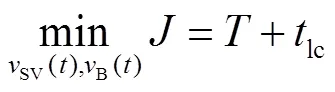
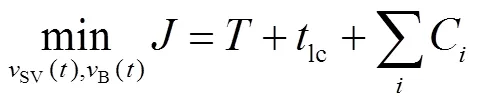
此外，约束式(19)(g)可以表达成式(21)：

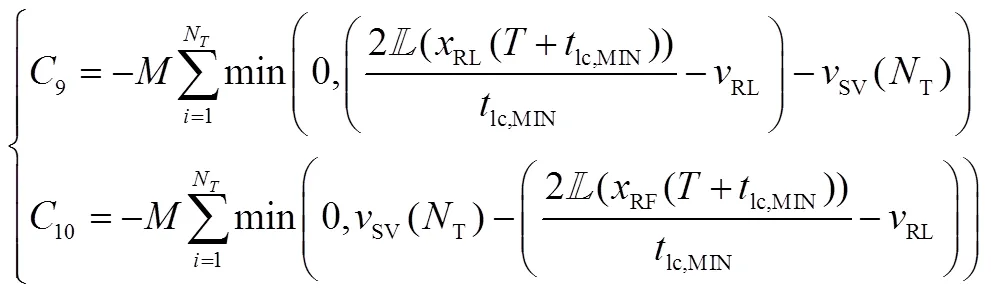
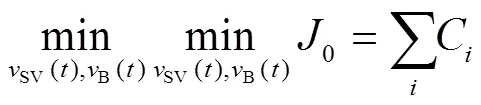
2.4 换道车辆群的换道规划

优化模型(式(20))针对的是单个换道需求，多个换道需求场景如图8(a)所示。绿色标识为换道需求车辆，也即需要进行换道的车辆。图中，车辆c3需要进行换道，间隙适配车辆可以是c1或者c2。车辆c11同样为换道需求车辆，但是由于c11和下游车辆间距较远，无需同时考虑c11和c3的换道需求。换道车辆群的换道规划需要(1)确定换道车辆群；(2)提取成对换道需求车辆和间隙适配车辆；(3)换道序列生成和规划。

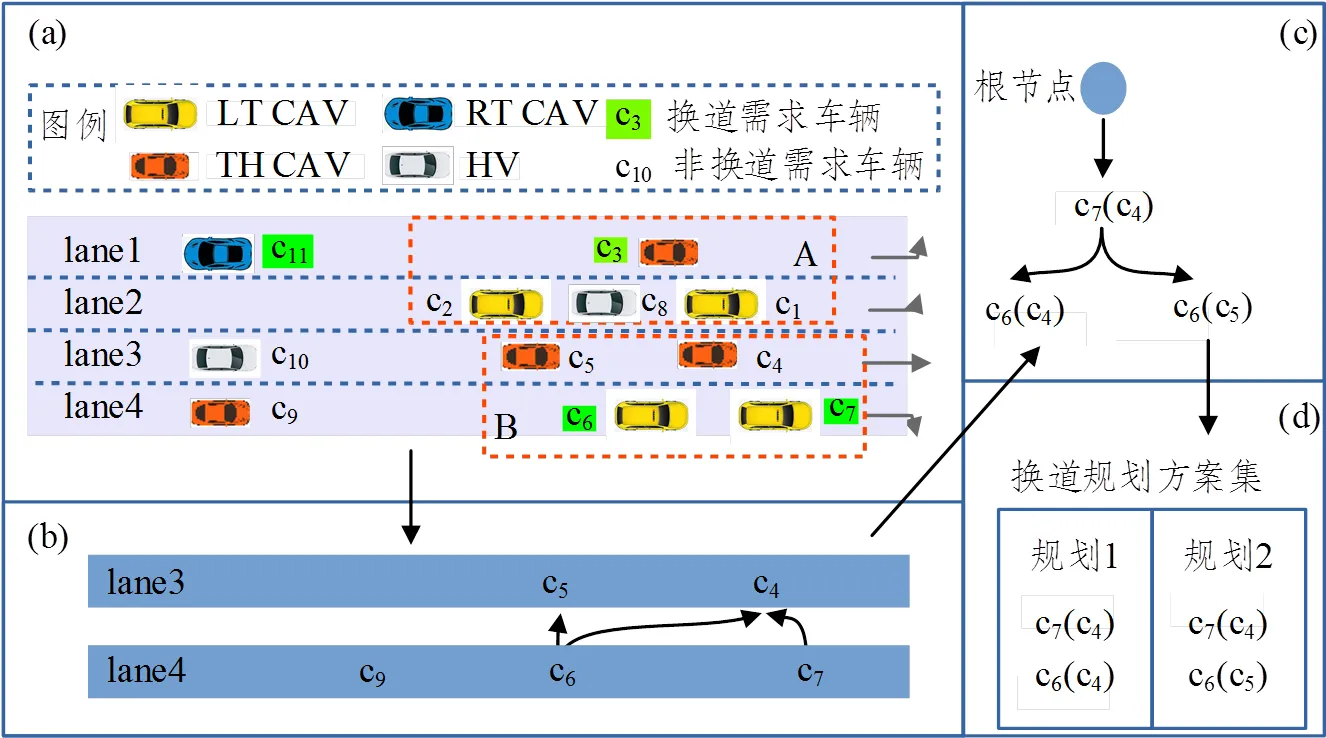
图8 换道车辆群构造示意图

2.4.1 换道车辆群划分

换道车辆群使换道行为产生相互影响，需要统筹考虑所有车辆，其中换道车辆群确定流程如图9所示。

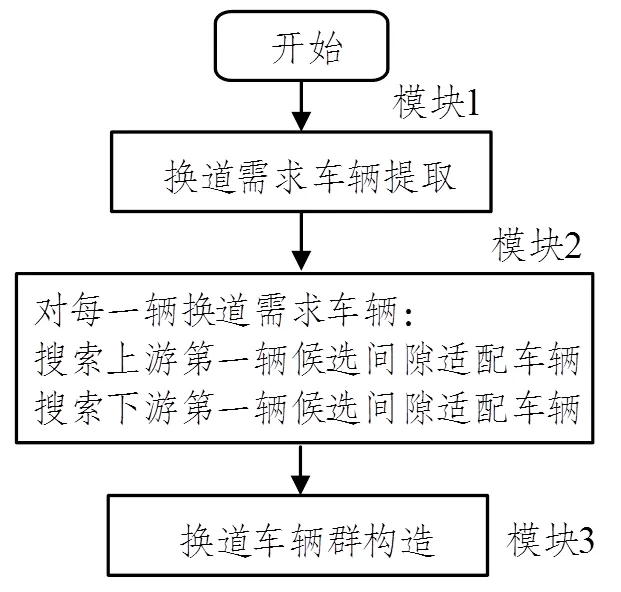
图9 换道车辆群构造流程

模块2中，任意一个换道需求车辆，其目标车道上只要存在CAV，那么该CAV就可能为换道需求车辆提供间隙适配机会。本文设定如下规则：(1)上游候选间隙适配车辆的搜索过程中，最多搜索5辆车；(2)一旦找到一辆间隙适配车辆，那么不会继续向上游搜索；(3)当车辆的纵向距离大于阈值时(此处设定为125m)，则认为车辆之间没有任何影响，从而以该阈值切割上游或者下游的换道车辆群。以图8(a)中的车辆c7为例，由于c7下游没有车辆，因此，没有下游候选间隙适配车辆，而上游第一辆CAV为c4。因此，车辆c7的上游间隙适配车辆为c4。此时，车辆c7的上下游间隙适配车辆搜索完毕，不会再向上游搜索。车辆c9进行搜索时，目标车道的下游第一辆CAV为c5，但是c10和c5间距大于阈值，因此c9不会与下游的CAV构成换道车辆群。因此，可将换道需求车辆和候选间隙适配车辆相连接，构成一个有向图。任意一条边从换道需求车辆指向间隙适配车辆，如图8(b)所示，该图用于生成模块3中的换道车辆群。

模块3中的换道车辆群构造基于模块2输出的有向图。该有向图对应的无向图中，任意一个孤立子图构成一个换道车辆群，例如图8(a)中的车群B，车辆c9也独自构成一个换道车辆群，但该换道车辆群无需进行间隙适配优化。

2.4.2 换道序列决策树生成

任意一辆换道需求CAV最多对应两辆间隙适配车辆。进行协同换道时，换道需求车辆所利用的间隙最多只有两种可能。协同换道的序列可以进行枚举生成，如图8(c)所示。枚举首先从最下游的换道需求车辆开始向上游追溯，这是考虑最下游车辆的换道需求最迫切，且下游换道需求车辆的间隙适配车辆的轨迹会影响上游车辆。

以图8(a)所示的车辆群B为例，首先从最下游的车辆c7开始。由于c7只对应车辆c4，因此，c7从根节点分支一个子节点c7(c4)，括号中为间隙适配车辆标识符；上游相邻车辆为c6，该车辆对应两个间隙适配车辆，因此，从节点c7(c4)进行分支，得到两个子节点(c6(c4)和c6(c5))，最终得到图8(c)中的换道序列决策树。

2.4.3 换道规划集及决策

输入·换道序列·人工驾驶车辆·每辆车(包括换道需求车辆和间隙适配车辆、人工驾驶车辆)的位置和速度 输出·每辆车的轨迹(加减速轨迹和换道轨迹)·车辆群间隙适配和换道所用时长 1 2For k=1 to n 3求解式(20)，对进行间隙适配优化，得到的加速段轨迹、 4换道轨迹、的适配轨迹 5For j=1 to 6车辆遵循IDM模型，计算其受前车影响的轨迹 7换道结束时刻，即为车辆群采用换道序列C所需时长

3 仿真实验与结果分析

本文利用数值仿真和软件仿真两种方法对模型进行分析。数值仿真展示CAV的具体换道轨迹，软件仿真说明模型对城市干道交通流的整体效果。假设人工驾驶车辆HDV遵循IDM跟驰模型，其表达形式如下：

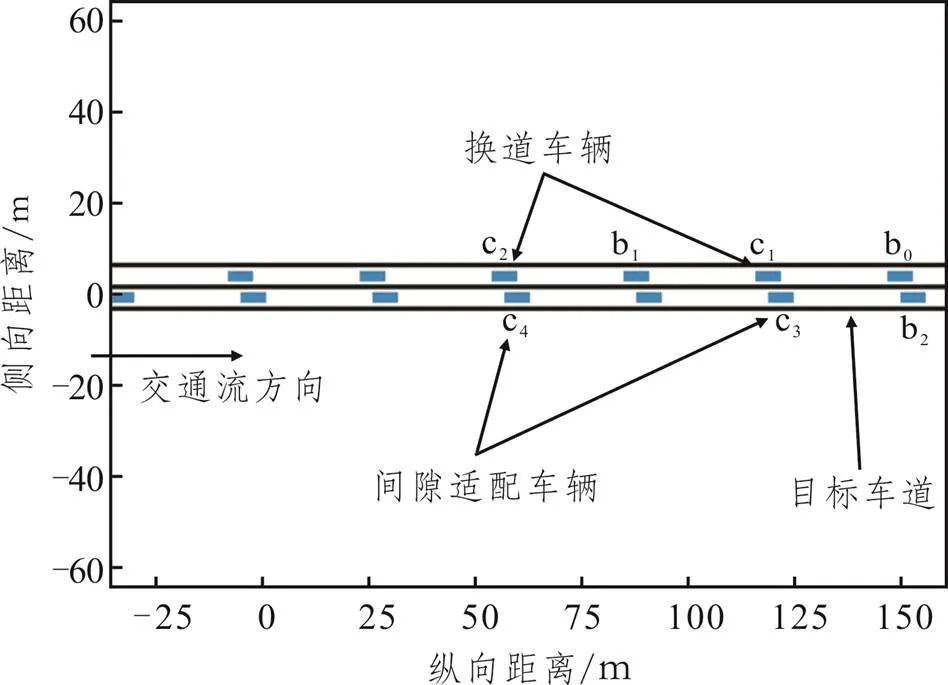
图11 多个换道请求共存下的仿真场景

考虑两个换道决策序列c1(c3)→c2(c3)以及c1(c3)→c2(c4)。首先，考虑第一个换道序列中的第一个换道请求c1(c3)，也即c3减速为c1提供换道机会。利用优化模型式(20)对c1和c3的轨迹进行协同优化，可得到图12、图13和图14为轨迹优化结果。其中，图12为换道车辆c1和间隙适配车辆c3的速度曲线。当速度调整完毕(图12中速度曲线终点对应时刻)，车辆c1即开始换道。从图12中可知车辆c3一直在减速，为c1制造可行间隙，而车辆c1首先减速再进行加速。分析可知，车辆b0的存在，c3需要首先减速扩大和b0的距离，然后进行换道。图13给出了本车道所有车辆的时空轨迹。车辆c1的轨迹分为三部分：减速等待间隙、换道和目标车道跟驰。第一部分轨迹的速度如图12所示，车辆在大约30s内完成了换道行为。从减速开始至换道完成，行驶距离约为200m。图14为目标车道所有车辆的轨迹，其中，第二辆车(也即车辆c3)的轨迹也分为三部分：减速进行间隙适配、恒速部分(为车辆c1换道提供可行性)和跟驰部分。第一部分轨迹的速度也如图12所示，整体而言，完成第一个换道请求大约需要30s。

第一个换道请求c1(c3)优化完毕后，再考虑第二个换道请求c2(c3)，第一个换道请求完成之后的轨迹作为第二个换道请求c2(c3)的输入。在优化车辆c2和c3的轨迹时，需要考虑车辆c2和前车的距离作为安全约束，换道请求c2(c3)规划的初始状态如图15所示。由于在优化c2时，假定c1已经完成换道，因此，c2车辆和前车的约束要考虑两段：第一段为图11中车辆b1的轨迹和c1的第三段轨迹(也即跟驰部分)，二者共同构成了车辆c2换道时的“本车道前车”。车辆c2轨迹规划时，既需要考虑和b1的距离，也需要考虑和c1第三部分轨迹的距离；第二段为c3进行间隙适配时，需要考虑的b2的轨迹和c1的第三部分轨迹。其中，c2(c3)轨迹优化结果如图16和图17所示。

图12 间隙适配车辆和换道车辆的速度

图13 本车道间隙适配和纵向轨迹优化结果

图14 目标车道间隙适配和轨迹优化结果

图15 换道请求c2(c3)规划时的初始状态

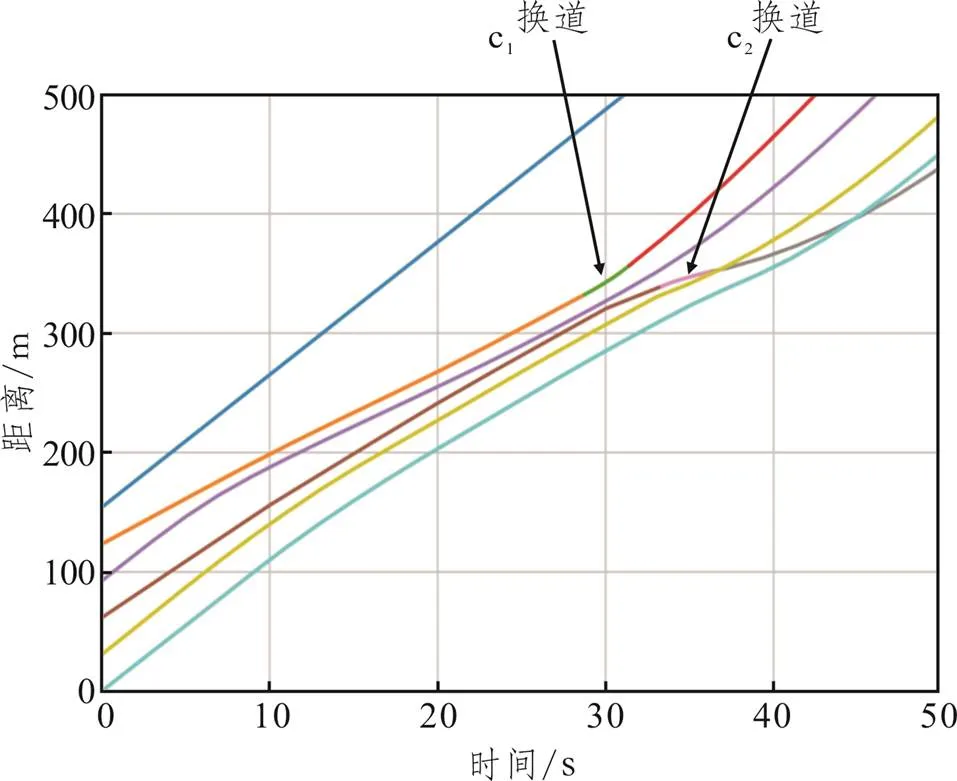
图16 本车道换道请求c2(c3)的间隙适配和纵向轨迹优化结果

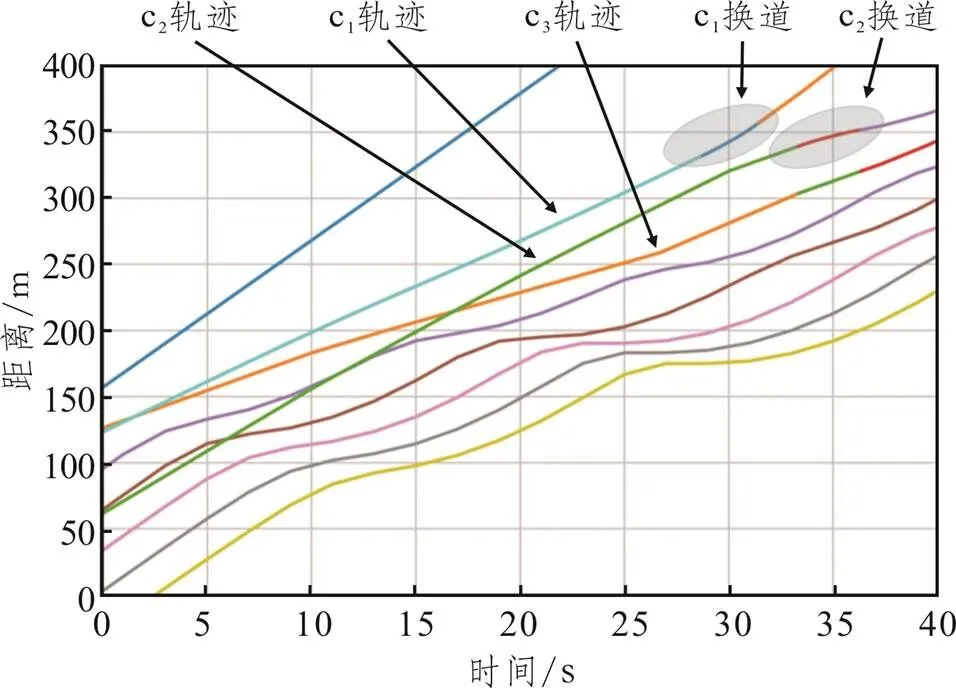
图17 目标车道换道请求c2(c3)的间隙适配和纵向轨迹优化结果

两辆CAV的纵向轨迹如图16所示，每个轨迹可分为三段：速度适配、换道和(换道完成时在目标车道)跟驰，且在大约35s时，两辆车都进入了目标车道。此外，图17给出了目标车道所有车辆的轨迹，从图中可知，优化的结果为c3持续进行减速，为c1以及c2制造可行间隙。车辆c1首先获得换道可行性进行换道，随后，车辆c2获得可行性间隙，并进行换道。整个换道过程持续约35s，换道距离(用车辆c1轨迹的初始位置和换道完成时的位置差来计算)约为200m。

图18为第二个换道序列c1(c3)至c2(c4)的轨迹规划结果。其中，车辆c3减速为c1进行间隙适配，车辆c4减速为c2提供间隙适配，且第一个换道和第二个换道发生时刻分别约为20s和30s。两个换道请求执行需要的空间距离(从车辆c1的位置开始计算)约150m。由图17可知，两个换道完成时间比第一个换道序列(见图14)短，换道执行所需要的纵向距离也比第一个换道序列短，因此，换道序列c1(c3)→c2(c4)优于换道序列c1(c3)→c2(c3)。综上，最终的换道轨迹采取第二个换道序列的优化结果(即图18)。

图18 目标车道换道序列c1(c3)→c2(c4)的轨迹优化结果

为了研究算法在宏观层面对交通流的影响，以图19(a)的城市道路为例，利用SUMO搭建仿真路段进行仿真。其中，路段分为展宽段和上游段，其中展宽段长度100m，上游段长度300m，上游段允许换道，信号参数如图19(b)所示。绿灯时间统一设定为40s，黄灯时间为3s；基准交通需求为直行流量300辆/h和左转流量100辆/h。基准流量乘以流量系数作为最终的输入流量。例如流量系数为2，则输入直行流量600辆/h，左转流量200辆/h，其中，右转流量设定为100辆/h不变。

图19 仿真场景

分析可知，若展宽段内直行车辆排队过长，则会堵塞展宽段入口。最左侧车道如果存在未顺利换至直行车道的车辆，则左转车辆被堵塞，进而影响交叉口的通过量。而基于本文提出的方法，可使车辆顺利完成换道，进而缓解交叉口的堵塞风险，提升整个交叉口的通过量。因此，利用仿真期间内的整个进口道实际通过的车辆数可验证本文提出方法的有效性。通过仿真，得到不同的需求水平下的通过量如表1所示。

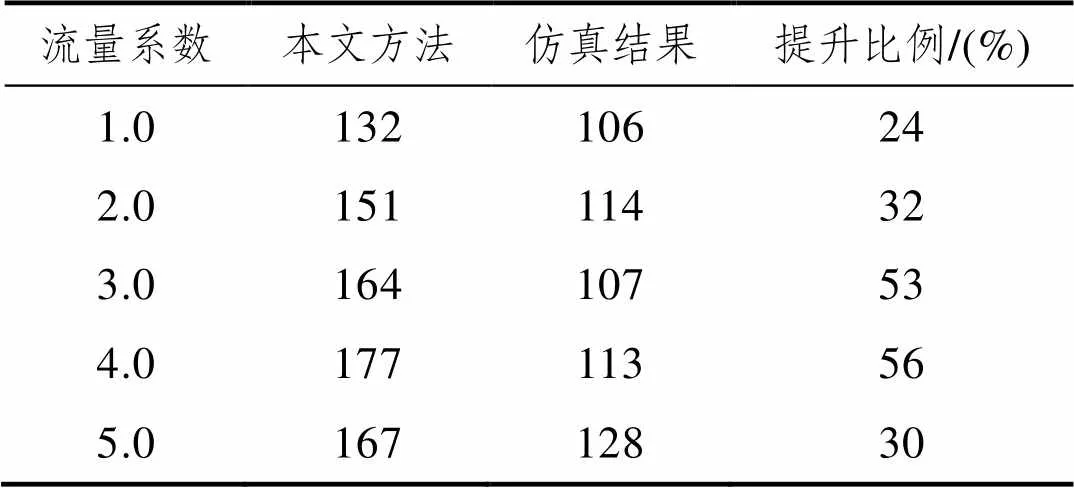
表1 算法通过量和仿真通过量对比

从表1可知，与没有协同换道相比，本文提出的方法在不同交通需求下的交叉口进口通过量均要高，最少可以提升24%。由表1的结果可知，即使信号参数不变，由于排队溢出和堵塞的存在，交叉口的通过量与输入流量未成正比关系。

4 结 语

本文提出了混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划方法。该方法利用多项式和三角函数，将单个换道需求下成对CAV的时空轨迹求解表达为最优控制模型。数值仿真表明，当目标车道的间隙不可行时，该方法可以对成对CAV进行时空轨迹优化，为换道需求车辆提供合适的换道间隙；当多个换道需求同时存在，本方法可遍历换道序列，对车辆群的换道过程进行整体优化。仿真结果表明，在不同交通需求水平下，应用本文方法后整体交通流运行状态得到了提升，因此，本文的方法可以降低换道失败车辆对交通流的影响。

道路交通流运行受到很多因素的影响，在进行轨迹优化时，本文需要进一步考虑HDV和CAV之间的博弈行为。同时，本文假设在规划初期能获得所有车辆的信息，然而混合自动驾驶车流的感知仍然需要进一步研究。

[1] 温惠英, 张伟罡, 赵胜. 基于生成对抗网络的车辆换道轨迹预测模型[J]. 华南理工大学学报(自然科学版), 2020, 48(5): 32-40.

[2] GIPPS PG. A model for the structure of lane-changing decision[J]. Transportation Research Part B: Methodological, 1986, 20(5): 403-414.

[3] YANG Q, KOUTSOPOULOS HN. A microscopic traffic simulator for evaluation of dynamic traffic management systems[J]. Transportation Research Part C: Emerging Technology, 1996, 4(3): 113-129.

[4] ZHENG Z, AHN S, CHEN D, et al. The effects of lane-changing on the immediate follower: anticipation, relaxation, and change in driver characteristics[J]. Transportation Research Part C: Emerging Technology, 2013, 26: 367-379.

[5] HIDAS P. Modelling lane changing and merging in microscopic traffic simulation[J]. Transportation Research Part C: Emerging Technology, 2002, 10(5-6): 351-371.

[6] HIDAS P. Modelling vehicle interactions in microscopic simulation of merging and weaving[J]. Transportation Research Part C: Emerging Technology, 2005, 13(1): 37-62.

[7] KESTINGA, MARTIN T, HELBING D. General lane-changing model MOBIL for car-following models[J]. Transportation Research Record: Journal of the Transportation Research Board, 2007, 1999(1): 86-94.

[8] AHMED K, BEN-AKIVA M, KOUTSOPOULOS H, et al. Models of freeway lane changing and gap acceptance behavior[J]. Transportation and Traffic Theory, 1996, 13: 501-515.

[9] TOLEDO T, KOUTSOPOULOS HN, BEN-AKIVA M. Integrated driving behavior modeling[J]. Transportation Research Part C: Emerging Technology, 2007, 15(2): 96-112.

[10] 高茹涵. 基于多传感器融合的自主换道控制策略研究[D]. 长春: 吉林大学, 2020.

[11] 刘志强, 韩静文, 倪捷. 智能网联环境下的多车协同换道策略研究[J]. 汽车工程, 2020, 42(3): 299-306.

[12] DO Q, TEHRANI H, MITA S, et al. Human drivers based active-passive model for automated lane change[J]. IEEE Intelligent Transportation Systems Magazine, 2017, 9(1): 42-56.

[13] NILLSSON J, BRANNSTROM M, COELINGH E, et al. Lane change maneuvers for automated vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(5): 1087-1096.

[14] 田勇达. 混流环境下智能网联车辆换道模型研究[D]. 长春: 吉林大学, 2020.

[15] 张荣辉, 游峰, 初鑫男, 等. 车-车协同下无人驾驶车辆的换道汇入控制方法[J]. 中国公路学报, 2018, 31(4): 180-191.

[16] 张家旭, 张振兆, 赵健, 等. 采用极点配置的自动驾驶汽车换道路径规划与跟踪控制[J]. 西安交通大学学报, 2020, 54(10): 1-8.

[17] ZHU S, AKSUN-GUVENC B. Trajectory planning of autonomous vehicles based on parameterized control optimization in dynamic on-road environments[J].Journal of Intelligent & Robotic Systems, 2020, 100(4): 1055-1067.

[18] KATZOURAKIS D, DE WINTER JC F, DE GROOT S, et al. Driving simulator parameterization using double-lane change steering metrics as recorded on five modern cars[J]. Simulation Modelling Practice and Theory, 2012, 26: 96-112.

[19] PEREZ J, GODOY J, VILLAGRA J, et al. Trajectory generator for autonomous vehicles in urban environments[C]//2013 IEEE International Conference on Robotics and Automation. Karlsruhe: IEEE, 2013: 409-414.

[20] AKCELIK R, BESLEY M. Acceleration and deceleration models[C]//23rd Conference of Australian Institutes of Transport Research(CAITR 2001). Melbourne: Monash University, 2001, 10-12.

[21] 柏海舰, 申剑峰, 卫立阳. 无人车“三阶段”换道轨迹规划过程分析[J]. 合肥工业大学学报(自然科学版), 2019, 42(5): 577-584, 676.

[22] 黄玲, 郭亨聪, 张荣辉, 等. 人机混驾环境下基于LSTM的无人驾驶车辆换道行为模型[J]. 中国公路学报, 2020, 33(7): 156-166.

[23] 兰凤崇, 李诗成, 陈吉清, 等. 考虑操纵稳定性的自动驾驶汽车轨迹综合优化方法[J]. 湖南大学学报(自然科学版), 2019, 46(10): 36-45.

[24] MA F, SHEN Y, NIE J, et al. Trajectory planning and tracking for four-wheel-steering autonomous vehicle with V2V communication[R]. Detroit: SAE Technical paper, 2020.

[25] SUN D, KONDYLI A. Modeling vehicle interactions during lane-changing behavior on arterial streets[J]. Computer-Aided Civil and Infrastructure Engineering, 2010, 25(8): 557-571.

[26] HILL C, ELEFTERIADOU L, KONDYLI A. Exploratory analysis of lane changing on freeways based on driver behavior[J]. Journal of Transportation Engineering, 2015, 141(4): 04014090.

[27] YANG M, WANGX, QUDDUS M. Examining lane change gap acceptance, duration and impact using naturalistic driving data[J]. Transportation Research Part C: Emerging Technologies, 2019, 104: 317-331.

[28] CHEN Y, LUC, CHU W. A cooperative driving strategy based on velocity prediction for connected vehicles with robust path-following control[J]. IEEE Internet of Things Journal, 2020, 7(5): 3822-3832.

[29] WANGZ, ZHAOX, XUZ, et al. Modeling and field experiments on autonomous vehicle lane changing with surrounding human-driven vehicles[J]. Computer-Aided Civil and Infrastructure Engineering, 2020, 36(7): 877- 889.

[30] LUOY, XIANGY, CAOK, et al. A dynamic automated lane change maneuver based on vehicle-to-vehicle communication[J]. Transportation Research Part C: Emerging Technologies, 2016, 62: 87-102.

Proactive Gap Adaption and Sequence Planning for Multiple Lane-changing Requests under Mixed Autonomous Vehicle Flow

QI Hong-sheng1, YING Yu-yan1, LIN Jun-shan2, YAO Zhi-Hong3

(1. Institute of Transportation Engineering, Zhejiang University, Hangzhou 310058, China; 2. Hainan Tropical Automobile Test Co. Ltd, Qionghai 571400, China; 3. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China)

During rush hours, the feasible gaps for the lane-changing behavior of vehicles decreases, and lane-changing duration increases. Vehicles that fail to change laneshave to wait and hence, block the upstream traffic flow. As connected and autonomous vehicles (CAVs) communicate and cooperate, a proactive gap adaption and lane-changing sequence planning model that works ina mixed CAV scenario when multiple lane-changing requests coexist was established in this study. First, polynomial and trigonometric functionswere employed to express the spatial trajectory and the speed profile during lanechanging, based on which the lane-changing feasibility criterion was established. Next, the feasible state setof the lane-changing initiation moment was constructed. The cooperative lane changing for a singlelane-changing request was formulated as an optimal control model. For multiplelane-changing requests, the lane-changing sequence was optimized as a whole. The numerical simulations show that the proposed model can optimize the spatial-temporal trajectory. The software simulations reveal that the model can decrease the influence of lane-changing behavior on throughput at different demand levels. The improvement was up to 24%.

intelligent transportation; connected automated vehicle（CAV）; lane changing; trajectory; gap; simulation

U491

A

10.19961/j.cnki.1672-4747.2021.04.031

1672-4747(2021)04-0036-16

2021-04-22

2021-06-02

2021-06-11

2021-04-22； 04-24～04-25； 05-07～05-08； 06-02

国家重点研发计划项目(2019YFB1600300)

祁宏生(1984—)，男，江苏盐城人，副教授，研究方向为交通控制和交通流理论，E-mail：qihongsheng@zju.edu.cn

姚志洪(1991—)，男，安徽安庆人，助理教授，研究方向为智能网联交通系统建模与优化，E-mail：zhyao@my.swjtu.edu.cn

祁宏生，应雨燕，林俊山，等. 混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划[J]. 交通运输工程与信息学报，2021, 19(4): 36-51.

QI Hong-sheng, YING Yu-yan, LIN Jun-shan, et al. Proactive Gap Adaption and Sequence Planning for Multiple Lane-changing Requests under Mixed Autonomous Vehicle Flow[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 36-51.

(责任编辑：李愈)