基于混合修正策略的随机时间车辆路径优化方法

马 俊，张纪会，郭乙运

基于混合修正策略的随机时间车辆路径优化方法

马 俊1, 2，张纪会1, 2，郭乙运3

(1. 青岛大学，复杂性科学研究所，青岛 266071；2. 山东省工业控制技术重点实验室，青岛 266071；3. 青岛港国际股份有限公司，青岛 266071)

针对带有随机旅行时间、随机服务时间及时间窗约束的车辆路径问题，建立了带修正策略的随机规划模型，并给出了两阶段求解方法。第一阶段运用改进遗传算法获取先验路径，第二阶段采用两种混合修正策略(分别记为A、B)调整“失败”的先验路径。混合修正策略A(B)通过随机模拟实验判断对当前顾客的延迟服务(对下一顾客的服务)是否会对该路径后续顾客造成大规模延迟服务，并采取相应的调整措施。基于Solomon算例进行了仿真实验，对小规模算例将仿真结果同CPLEX求解结果作对比；对大规模算例将仿真结果同已知最优解作对比。结果表明：所给算法可获得小规模算例的精确解，大规模算例的近似最优解。同时，对比不同策略下的仿真结果表明两种混合修正策略具有优越性，研究结果对随机车辆路径问题的求解具有一定的参考意义。

物流工程；车辆路径；随机旅行及服务时间；随机规划；混合修正策略；改进遗传算法

0 引 言

车辆路径问题(Vehicle Routing Problem，VRP)是Dantzig和Ramser[1]提出的一类经典组合优化问题。自提出至今，已应用于众多领域，如物流配送、垃圾回收[2]、上门维修及医疗服务等，并演化出许多不同问题，如带容量或时间窗约束的VRP等，有关VRP的最新研究综述参见文献[3]。传统VRP一般假设所涉及的参数信息是已知的，然而在现实世界中某些信息是无法提前获知的，如车辆在某一路段的实际运行时间、车辆在某一顾客点的实际服务时间、顾客的实际需求等，为此衍生出许多不确定VRP问题。不确定性可进一步分为主观不确定性和客观不确定性，常用模糊变量或随机变量表示。由于主观不确定性可随研究的深入而逐渐清晰，故客观不确定性VRP的研究更为广泛和深入[4-6]。从客观不确定性角度出发，本文研究带有随机旅行时间、随机服务时间及时间窗约束的车辆路径问题(Vehicle Routing Problem with Stochastic Travel and Service Time and Time Windows，VRPSTSTW)。

不确定VRP的建模方法主要有三种：机会约束规划(Chance-Constrained Programming, CCP)、带修正策略的随机规划(Stochastic Programming with Recourse, SPR)及鲁棒优化(Robust Optimization, RO)。CCP将随机VRP描述为求解一个或多个约束条件需满足一定置信水平的最优化问题，求解该问题的难点在于机会约束检查，两种常见的方法为离散化方法和随机模拟方法。离散化方法将随机变量(如旅行时间及服务时间)分布函数离散为有限个数值()-累计概率(())对，求解待检查随机变量(如到达时间)分布函数并检查机会约束；随机模拟方法通过大量模拟实验获得给定路径上待求变量样本均值等统计信息，以样本均值近似估计期望值并检查机会约束。基于离散化方法，Miranda和Conceicao[7]、Zhang等[8]求解了单目标VRPSTSTW, Miranda等[9]求解了多目标VRPSTSTW。基于随机模拟方法，Li等[10]检查了车辆到达时间及司机工作时长机会约束。CCP模型下的最优路径是在一定置信水平下求得的，实际运行中存在“失败”的可能性。SPR运用修正策略对车辆实际运行中发生“失败”的先验路径给予修正。这里“失败”路径是指车辆沿先验路径行驶过程中，由于随机因素的存在，使得车辆无法按照顾客要求提供服务。随机VRP修正策略多围绕不确定顾客需求展开，常见的修正策略有返回车场补货、预防性补货等。返回车场补货策略指的是如果车辆在某一顾客处的现有存货不足以完全满足当前顾客实际需求，车辆需先返回车场补货，然后完成对该顾客的服务，参见文献[11]。预防性补货指的是车辆在完成某一顾客服务后，判断现有存货满足下一顾客需求的概率大小，若该概率值小于某一设定阈值，车辆立即返回车场补货，然后行驶至未服务顾客处，参见文献[12]。此外，Salavati- Khoshghalb等[13]针对不确定需求VRP，提出了一种混合预防性补货、风险评估及距离评估的修正策略。针对VRPSTSTW，常见的修正策略有两种，分别称之为TWVC(Time Windows Violation Cost, TWVC)及跳过策略。TWVC允许顾客接受车辆提供的延迟服务；跳过策略指的是，当车辆到达某一顾客的时间晚于该顾客要求的右时间窗时，为保证对下一顾客的准时服务，车辆跳过当前顾客。Li等[10]将VRPSTSTW分别建模为CCP和SPR，其修正策略是对违反时间窗及司机工作时长约束的车辆按照违反程度添加一定的线性惩罚成本。Andres等[14]提出了结合机会约束及修正策略的混合随机规划模型，其修正策略为跳过策略。与CCP和SPR不同的是，RO以不确定集的形式体现不确定性，目标是寻找不确定集中最糟糕情形下对应的最优解。基于该思想，Shi等[15]在上门医疗服务路径规划中考虑不确定旅行及服务时间，运用Gurobi、模拟退火算法、禁忌搜索算法、变邻域局部搜索算法分别求解该RO模型，并通过一系列实验验证了模型和算法的有效性。此外，该文进一步分析了实例中时间窗宽度、顾客分布位置等因素对结果的影响。针对带有不确定服务时间道路网络日常维护中的弧路由问题(Arc Routing Problem, ARP)，Chen等[16]将该问题建模为RO，并设计了分支定界算法，同时将RO与经典的CCP进行比较，验证了运用RO所得路径的优越性。近年来，有关随机VRP问题的研究多围绕在线决策展开，如采用动态规划[17]、马尔科夫过程[18]、滚动算法[19]等，有关随机动态VRP的最新研究综述参见文献[20]。实时决策要求决策者在极短时间内给出有效决策，对许多算法带来了巨大挑战。强化学习可快速实现端到端的输出，将其同随机动态VRP结合，可进一步推动该领域相关研究进展，有关强化学习在组合优化领域的研究综述，参见文献[21, 22]。

对于VRPSTSTW，车辆沿先验路径行驶过程中，存在到达时间晚于顾客右时间窗的可能。若车辆在某一顾客处的到达时间大于规定的右时间窗，此时存在两种选择，延迟服务或跳过，分别对应TWVC跳过策略。无论TWVC还是跳过策略均存在不足，TWVC下顾客接受车辆提供的延迟服务，存在对某一顾客的延迟服务造成该路径后续多个顾客延迟服务的可能；相反，采用跳过策略时，顾客不接受晚到车辆提供的延迟服务，很大程度上保证了该路径后续顾客的准时服务，但此举可能大幅增加企业运营成本。实际上，车辆在任一顾客处的迟到时间有长有短，迟到程度的大小(如迟到1s与迟到1h)对后续顾客服务过程造成的影响不同，应当依据影响程度大小采取不同的应对措施。基于这个动机，本文提出了两种混合修正策略，根据对顾客不同程度的延迟采取不同的应对措施，这一点符合常识。

本文的贡献与创新：(1)指出影响程度大小可由后续顾客延迟服务数量反映；(2)定义顾客服务水平为准时服务顾客数量与该路径总的顾客数量的比值，即时间窗内获得服务顾客的比例；(3)提出两种混合修正策略(分别记为A、B)，两种混合修正策略均通过随机模拟实验近似量化当前决策(延迟服务或跳过)对后续顾客服务过程的影响，根据量化结果采取不同的调整措施，以实现提升顾客服务水平和降低运营成本的目的。

1 模型及混合修正策略

1.1 带修正策略的随机规划模型

VRPSTSTW的SPR模型为：

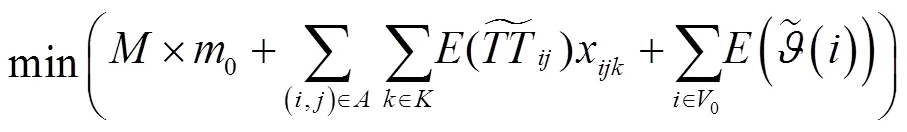
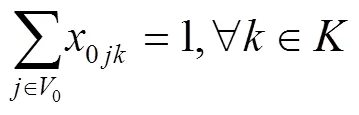
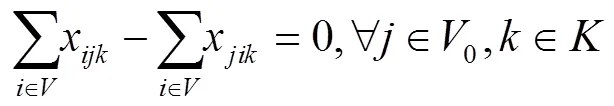
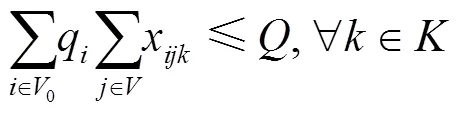
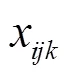
1.2 混合修正策略

(1)混合修正策略A

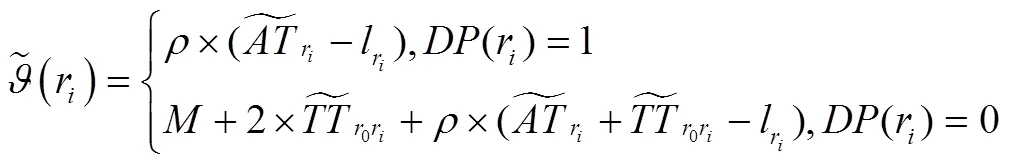
(2)混合修正策略B

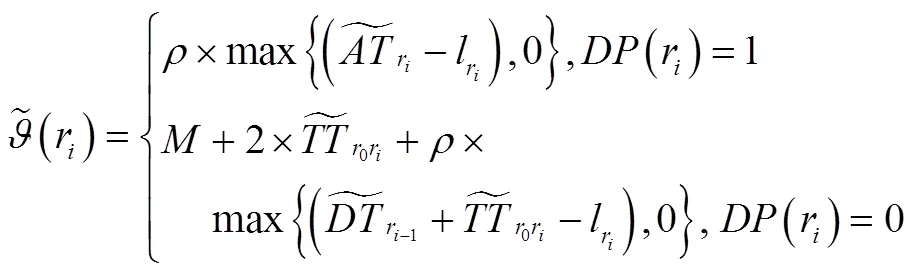
混合修正策略A与B的区别如下：混合修正策略A给出是否为当前顾客提供延迟服务的决策，而混合修正策略B给出是否服务下一顾客的决策。相对于混合修正策略A，混合修正策略B预先判断是否服务下一顾客，若是，车辆继续行驶至下一顾客，此时车辆能否在下一顾客要求的时间窗内到达是不确定的；反之，车辆跳过对下一顾客的服务，从车场在当前时刻立即派出空闲车辆为该顾客提供服务，故空闲车辆有可能在该顾客要求的时间窗内提供服务。

2 求解算法

SPR分两个阶段求解VRPSTSTW：第一阶段，根据先验知识确定先验路径；第二阶段，对车辆按照既定路径实际行驶过程出现的“失败”给予修正，其目标函数为最小化第一阶段路径总成本及第二阶段“失败”条件下的路径修正成本。基于旅行时间和服务时间的均值，运用改进遗传算法获取先验路径，后采用随机模拟方法求解混合修正策略下给定先验路径的平均修正成本及顾客服务水平。

2.1 改进遗传算法

遗传算法是应用最为广泛、最为成功的元启发式算法之一，其核心思想源于生物进化理论“物竞天择，适者生存”。对一个种群而言，种群中个体对应的适应度值不同，个体获得繁衍后代的机会不同，适应度值高的个体在遗传运算中被选择的概率较大，适应度值低的个体则以很大概率被淘汰，因此，对某一种群而言，经过一定的进化次数后，可以得到一个适应度值普遍较高的种群。遗传算法常用于求解VRP及其变形问题[25, 26]，本文在传统遗传算法的基础上，对种群中的个体添加局部搜索策略，具体的算法步骤如下：

Step1 编码

Step2 计算个体适应度

Step3 正比选择策略

正比选择策略，即每个个体被选中进行遗传运算的概率为该个体的适应度值和所有被选择个体适应度值总和的比值。

Step4 顺序交叉策略

顺序交叉策略可以较好地保持顾客间的相邻关系，适用于VRP的求解[13]。该策略随机生成两个交叉点，对交叉点间配对个体的部分基因进行交换并恢复个体合法性，交叉过程如图1所示。

父代P1= 1 23 4 5 6交叉子代 P1’= 2 3 4 1 5 6 父代P2= 3 24 16 5子代 P2’= 2 1 3 4 6 5 交叉点交叉点

Step5 变异操作

采用倒位变异方法，即随机地在染色体上选取两个倒位点并顺序翻转倒位点间的顾客位置，变异过程如图2所示。

倒位点1倒位点2 变异 父代P= 1 3 4 2 5 6 子代 P’= 1 3 2 4 5 6

Step6 局部搜索操作

对完成遗传运算后的个体添加局部搜索策略，该局部搜索策略由破坏和修复算子、交换算子及插入算子组成(以不同概率选择不同局部搜索算子)，各算子说明如下：

(1)破坏与修复算子

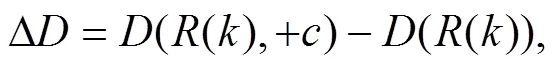
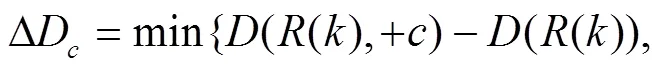
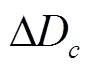
(2)交换算子

交换算子，即随机地在染色体上选取两个顾客并交换其位置。

(3)插入算子

插入算子，即随机地在染色体上选取两个顾客，并将第一个顾客插入到第二个顾客位置之后。

Step7 筛选新种群

将经过遗传运算后得到的子代种群混入父代种群中，并按照个体的适应度值大小进行降序排列，保留前个个体，其中为种群规模。

Step8 停止准则

双重停止准则：以最大迭代次数或连续次种群最优解不发生变化为算法停止准则。

2.2 随机模拟实验

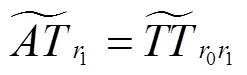
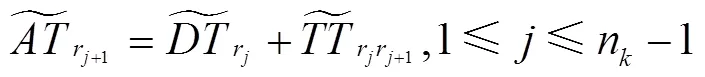
运用文献[10，14]中判断路径可行性及计算“失败”条件下期望路径修正成本的随机模拟方法，分别求解两种混合修正策略下某一给定路径的平均修正成本及顾客服务水平。求解算法中所涉及的变量符号及表示含义同上文一致。整个算法分为三个部分：第一部分计算混合修正策略A下给定路径的平均修正成本及顾客服务水平；第二部分计算混合修正策略B下给定路径的平均修正成本及顾客服务水平；第三部分判断车辆在顾客处应执行何种修正策略。算法流程如下：

(1)混合修正策略A

Step1 令=1，1=0，2=0，为随机模拟执行的次数。

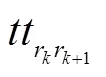
(2)混合修正策略B

Step1 令=1，1=0，2=0，为随机模拟执行的次数。

Step6 置=+1，转Step2。

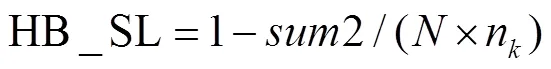
(3)选择修正策略的随机模拟实验

Step1 令=1，=0，为随机模拟执行的次数。

第3部分涉及混合修正策略A、B与跳过策略、TWVC之间的相互比较，由于跳过策略与TWVC的随机模拟实验与上述算法相似，故此处不再一一给出。

3 仿真试验及结果分析

3.1 案例选择

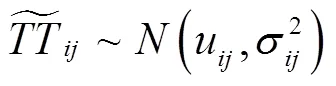
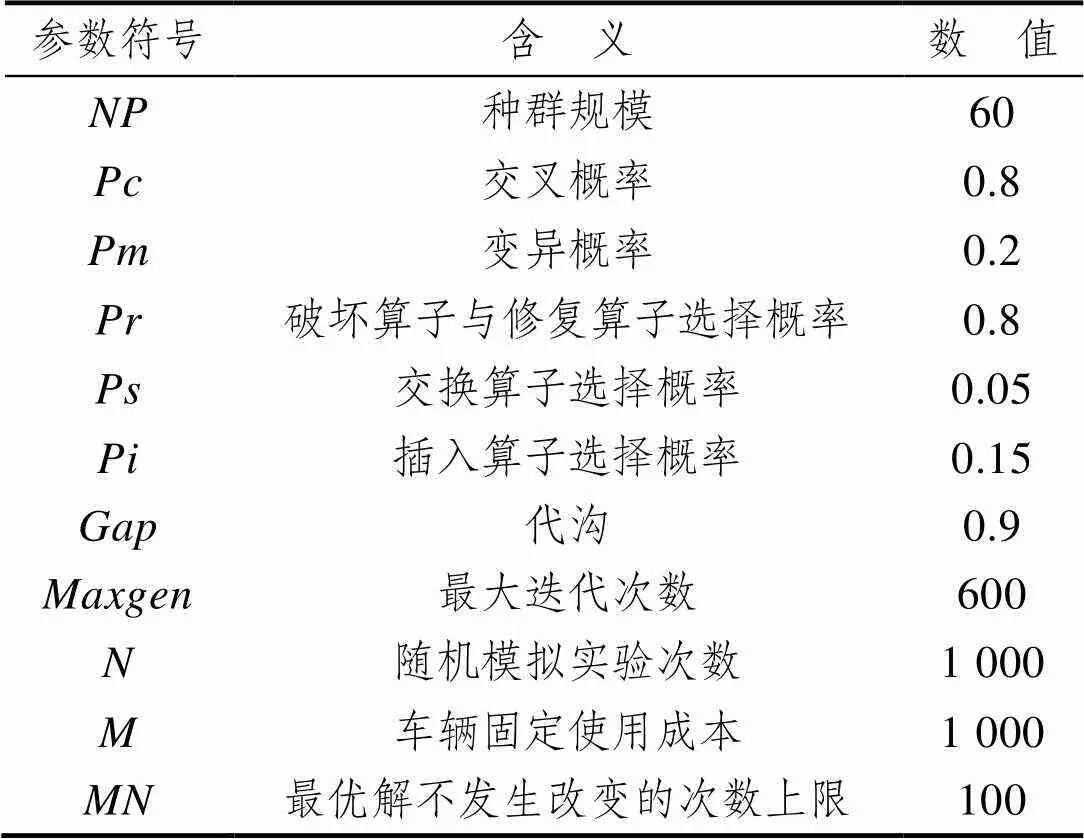
表1 改进遗传算法及随机模拟参数设置

3.2 实验结果及分析

运用改进遗传算法、CPLEX求解器以及混合修正策略，对部分Solomon算例进行实验，实验结果如表2(25个顾客)、表3(100个顾客)所示。相关说明如下：表2中每一算例下的结果为10次实验中的平均值；表3中每一算例下的结果为10次实验中的最优值；DC为先验路径对应的车辆运输距离、VEH为先验路径使用的车辆数；SC_COST、HA_COST、HB_COST及TWVC_COST分别为跳过策略、混合修正策略A、混合修正策略B及TWVC下的平均路径修正成本；SC_SL、HA_SL、HB_SL及TWVC_SL分别为跳过策略、混合修正策略A、混合修正策略B及TWVC下的平均顾客服务水平。

表2 实验结果(25个顾客)

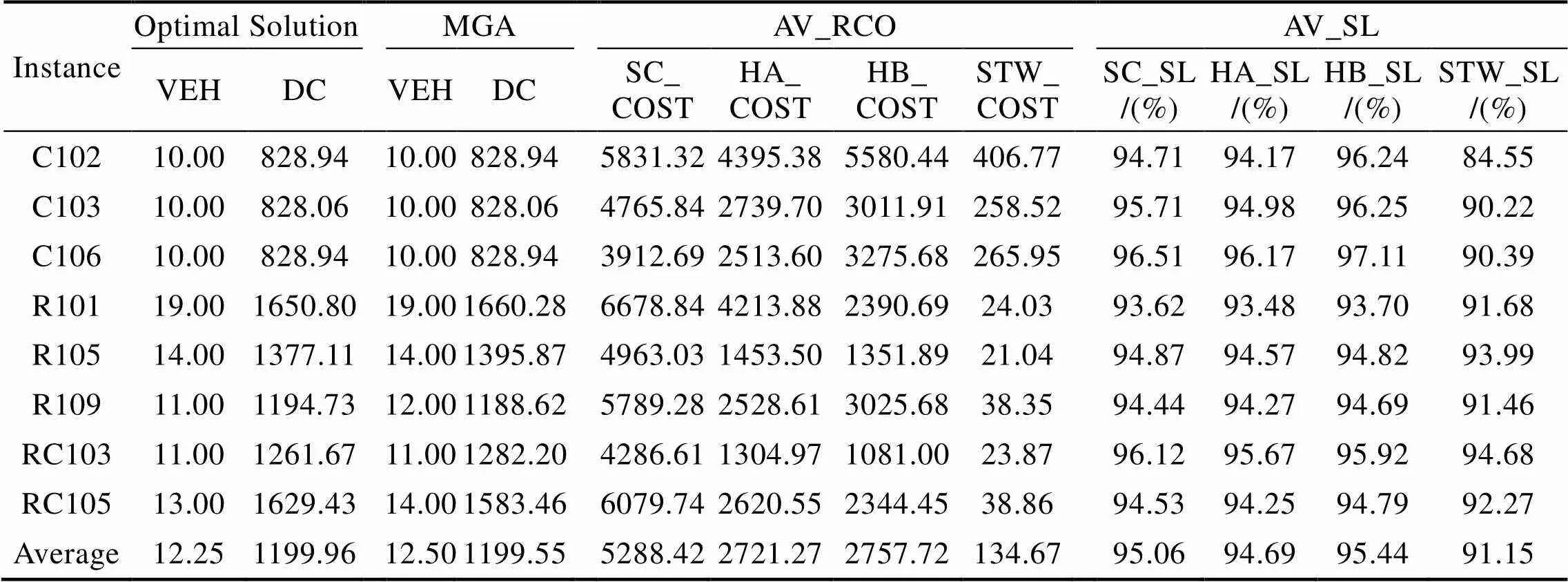
表3 实验结果(100个顾客)

由表2中第2列～第5列可知，文中给出的改进遗传算法能够找到小规模算例的精确解。由第6列～第13列知，四种修正策略对应的平均路径修正成本大小关系为SC_COST > HA_COST > HB_COST >TWVC_COST，平均顾客服务水平对应的大小关系为HB_SL > SC_SL > HA_SL > TWVC_SL。相对于TWVC，跳过策略对应的顾客服务水平增加了2.42%，其相应的路径修正成本增加了1 275.09。混合修正策略A对应的顾客服务水平增加了2.23%，其路径修正成本同样增加了667.14。由这四个数据可知，混合修正策略A相对跳过策略以7.98%(服务水平降低了0.19%)的顾客服务水平损失换取47.68%(成本减少了607.95)的路径修正成本节省，两者比值为5.97。因此，混合修正策略A可以在保持同跳过策略近似顾客服务水平的同时大幅降低路径修正成本。相对于跳过策略，混合修正策略B对应的顾客服务水平增加了0.47%，其对应的路径修正成本减少了709.75(占跳过策略修正成本的54.69%)，即混合修正策略B在顾客服务水平、路径修正成本两个层面均优于跳过策略。相对于混合修正策略A，混合修正策略B对应的路径修正成本降低了101.80、顾客服务水平增加了0.67%，即混合修正策略B在路径修正成本、顾客服务水平两个层面均优于混合修正策略A。

由表3中第2列～第5列可知，文中给出的改进遗传算法能够找到大规模算例的近似最优解。表3可得出与表2一致的结论，唯一区别是混合修正策略B下的平均路径修正成本略大于混合修正策略A，原因在于混合修正策略B在判断下一顾客是否服务时存在误判的可能性，该误判使得本可以按照TWVC修正的顾客改用跳过策略修正，进而造成对应路径的修正成本略大于混合修正策略A的情况。误判多发生在C1系列，原因在于C1系列为聚类型案例，其发生“失败”的可能性较大，故误判的比例也相对较高。此外，当文中TWVC的惩罚系数较大时，混合修正策略A、B均在顾客服务水平、路径修正成本两个层面上优于TWVC。

由实验结果分析可知：改进遗传算法能够找到小规模算例的精确解，大规模算例的近似最优解；混合修正策略B在顾客服务水平、路径修正成本两个层面上均优于跳过策略、混合修正策略A；混合修正策略A可以在近似保持跳过策略高服务水平的同时大幅降低其路径修正成本。跳过策略、混合修正策略A和B相对于TWVC均可大幅提升顾客服务水平，当TWVC下惩罚系数较小时，三种策略对应的路径修正成本均会增加，此时需要决策者权衡顾客服务水平与运营成本之间的权重。

4 总结与展望

针对VRPSTSTW，构建了SPR模型，同时给出了求解该模型的改进遗传算法以及两种混合修正策略。基于标准Solomon算例进行仿真实验，结果表明：改进遗传算法能够找到小规模算例的精确解，大规模算例的近似最优解；混合修正策略A、B均可显著降低跳过策略下的高路径修正成本，同时提高TWVC下的低顾客服务水平。此外，该实验结果也进一步表明当车辆在某一顾客处的到达时间略大于右时间窗时，即对该顾客的延迟服务并不会对该路径后续顾客服务过程造成较大影响时，采用延迟服务的决策可获得较优结果。

本文构建的随机VRP模型与实际VRP仍存在一定差距，进一步的研究方向包括：(1)时变网络可有效反映路网动态性，故可进一步研究时变网络下的随机VRP，或随机变量分布函数随时间发生变化的VRP，该类问题更具实际意义； (2)现有的适用于求解时间窗约束下随机时间VRP的修正策略较少，提出更具实用性及可操作性的修正策略是值得关注的重点；(3)利用运输过程中实时更新的有关数据，及时调整车辆运行路径并不断促进车辆间的相互合作，以丰富现有修正策略；(4)借助信息通信技术收集的关于整个运输过程的数据，搭建不确定环境下基于闭环数据驱动模式的、具备反馈机制的、可实时在线学习的车辆路径优化系统。

[1] DANTZIG G, RAMSER J. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80-91.

[2] 赵红霞, 刘高森, 李愈. 基于随机游走的分类垃圾回收最优路径规划[J]. 交通运输工程与信息学报, 2018, 16(3): 103-108.

[3] BRAEKERS K, RAMAEKERS K, NIEUWENHUYSE I V. The vehicle routing problem: state of the art classification and review[J]. Computers & Industrial Engineering, 2016, 99: 300-313.

[4] OYOLA J, ARNTZEN H, WOODRUFF D L. The stochastic vehicle routing problem, a literature review, part I: models[J]. Euro Journal on Transportation & Logistics, 2018, 7(3): 193-221.

[5] OYOLA J, ARNTZEN H, WOODRUFF D L. The stochastic vehicle routing problem, a literature review, part Ⅱ: solution methods[J]. Euro Journal on Transportation & Logistics, 2017, 6(4): 349-388.

[6] GENDREAU M, JABALI O, REI W. Future research directions in stochastic vehicle routing[J]. Transportation science, 2016, 50(4): 1163-1173.

[7] MIRANDA D M, CONCEICAO S V. The vehicle routing problem with hard time windows and stochastic travel and service time[J]. Expert Systems with Applications, 2016, 64: 104-116.

[8] ZHANG J L, LAM W H, CHEN B. A stochastic vehicle routing problem with travel time uncertainty: trade-off between cost and customer service[J]. Networks & Spatial Economics, 2013, 13(4): 471-496.

[9] MIRANDA D M, BRANKE J, CONCEICAO S V. Algorithms for the multi-objective vehicle routing problem with hard time windows and stochastic travel time and service time[J]. Applied Soft Computing, 2018, 70: 66-79.

[10] LI X Y, TIAN P, LEUNG S. Vehicle routing problems with time windows and stochastic travel and service times: models and algorithm[J]. International Journal of Production Economics, 2010, 125(1): 137-145.

[11] ZHANG J L, LAM W H, CHEN B. On-time delivery probabilistic models for the vehicle routing problem with stochastic demands and time windows[J]. European Journal of Operational Research, 2016, 249(1): 144-154.

[12] SALAVATI-KHOSHGHALD M, GENDREAU M, JABALI O, et al. An exact algorithm to solve the vehicle routing problem with stochastic demands under an optimal restocking policy[J]. European Journal of Operational Research, 2018, 273(1): 175-189.

[13] SALAVATI-KHOSHGHALD M, GENDREAU M, JABALI O, et al. A hybrid recourse policy for the vehicle routing problem with stochastic demands[J]. Euro Journal on Transportation & Logistics, 2019, 8(3): 269-298.

[14] ANDRES G, LAURENCE D, NACIMA L, et al. A multi-population algorithm to solve the vrp with stochastic service and travel times[J]. Computers & Industrial Engineering, 2018, 125: 144-156.

[15] SHI Y, BOUDOUH T, GRUNDER O. A robust optimization for a home health care routing and scheduling problem with consideration of uncertain travel and service times[J]. Transportation Research Part E Logistics and Transportation Review, 2019, 128: 52-95.

[16] CHEN L, GENDREAU M, HA M H, et al. A robust optimization approach for the road network daily maintenance routing problem with uncertain service time[J]. Transportation research Part E Logistics and transportation review, 2016, 85: 40-51.

[17] 周鲜成, 王莉, 周开军, 等. 动态车辆路径问题的研究进展及发展趋势[J]. 控制与决策, 2019, 34(3): 449-458.

[18] ULMER M W, GOODSON J C, MATTFELD D C, et al. On modeling stochastic dynamic vehicle routing problems[J]. Euro Journal on Transportation and Logistics, 2020, 9(2): 100008.

[19] GOODSON J C, THOMAS B W, OHLMANN J W. A rollout algorithm framework for heuristic solutions to finite-horizon stochastic dynamic programs[J]. European Journal of Operational Research, 2017, 258(1): 216-229.

[20] RITZINGER U, PUCHINGER J, HARTL R F. A survey on dynamic and stochastic vehicle routing problems[J]. International Journal of Production Research, 2016, 54(1): 215-231.

[21] 李凯文, 张涛, 王锐, 等. 基于深度强化学习的组合优化研究进展[J/OL]. 自动化学报: 1-22[2020-12-09]. https: //kns. cnki. net/kcms/detail/11. 2109. tp. 20201207. 1738. 001. html.

[22] 徐翔斌, 李志鹏. 强化学习在运筹学的应用: 研究进展与展望[J]. 运筹与管理, 2020, 29(5): 227-239.

[23] ULMER M W, STRENG S. Same-Day delivery with pickup stations and autonomous vehicles[J]. Computers & Operations Research, 2019, 108: 1-19.

[24] GOEL R, MAINI R, BANSAL S. Vehicle routing problem with time windows having stochastic customers demands and stochastic service times: Modelling and solution[J]. Journal of Computational Science, 2019, 3: 1-10.

[25] 徐菱, 胡小林, 胡小亮. 时间窗约束下需求可拆分的拣选与配送联合优化问题研究[J]. 交通运输工程与信息学报, 2020, 18(2): 18-29.

[26] 张传琪, 张杨. 动态路网下多车型车辆路径问题研究[J]. 交通运输工程与信息学报, 2017, 15(2): 112-118.

[27] 林清国. 基于混合遗传算法的有时间窗车辆路径问题研究[D]. 济南: 山东大学, 2007.

[28] SHAW P. Using constraint programming and local search methods to solve vehicle routing problems[C]// In Proceedings of the 4th International Conference on Principles and Practice of Constraint Programming. Berlin: Springer, 1998, 1520: 417-431.

[29] CHEN L, HA M H, LANGEVIN A, et al. Optimizing road network daily maintenance operations with stochastic service and travel times[J]. Transportation Research Part E Logistics and Transportation Review, 2014, 64: 88-102.

[30] EMEC U, CATAY B, BOZKAYA B. An adaptive large neighborhood search for an e-grocery delivery routing problem[J]. Computers & Operations Research, 2016, 69: 109-125.

[31] TURNER S, EISELE W, BENZ R. Travel time data collection handbook[R]. Texas: Texas Transportation Institute and Federal Highway Administration, 1998.

[32] EHMKE J, CAMPBELL A, URBAN T. Ensuring service levels in routing problems with time windows and stochastic travel times[J]. European Journal of Operational Research, 2015, 240(2): 539-550.

Hybrid Recourse Policy for the Vehicle Routing Problem with Stochastic Time

MA Jun1, 2，ZHANG Ji-hui1, 2，GUO Yi-yun3

(1. Institute of Complexity Science, Qingdao University, Qingdao 266071, China; 2. Shandong Key Laboratory of Industrial Control Technology, Qingdao 266071, China; 3. Qingdao Port Int. Co. Ltd., Qingdao 266071, China)

For the vehicle routing problem with stochastic travel and service time, and time windows, this study provides a stochastic programming model with a recourse and two-stage solving method. In the first stage,a modified genetic algorithm is used to find a prior route;in the second stage,two hybrid recourse policies (denoted by A and B, respectively) are designed to recourse the failure route. Based on a stochastic simulation experiment, the hybrid recourse policy denoted as A (B) determines whether the delayed service to the current customer (the service to the next customer) will cause a large-scale delayed service to the subsequent customers in the prior route, and makes a corresponding decision. Based on the Solomon benchmarks, the superiority of the two hybrid recourse policies and effectiveness of the modified genetic algorithm are shown, respectively, by comparing the experimental simulation results with those of the common recourse policies and the CPLEX Optimizer.The results have an unequivocal significance as a reference for how to solve the stochastic vehicle routing problem.

logistics engineering;vehicle routing;stochastic travel and service time; stochastic programming; hybrid recourse policy; modifiedgenetic algorithm

U492.3+12

A

10.19961/j.cnki.1672-4747.2021.04.039

1672-4747(2021)04-0087-11

2021-04-29

2021-06-28

2021-07-01

2021-04-29～05-06; 06-26; 06-28

国家自然科学基金项目(61673228, 62072260); 青岛市科技计划项目(21-1-2-16-zhz)

马俊(1995—)，男，硕士研究生，研究方向：物流系统工程，E-mail: qdumjun1001@163. com

张纪会(1969—), 男, 教授, 主要研究方向: 智能优化理论与方法、物流系统工程, E-mail: zhangjihui@qdu. edu. cn

马俊，张纪会，郭乙运. 基于混合修正策略的随机时间车辆路径优化方法[J]. 交通运输工程与信息学报，2021, 19(4):87-97.

MA Jun，ZHANG Ji-hui，GUO Yi-yun. Hybrid Recourse Policy for the Vehicle Routing Problem with Stochastic Time[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 87-97.

(责任编辑：李愈)