考虑自动驾驶的混合交通流路段阻抗函数
2021-12-16姚志洪郝慧君巫雪梅蒋阳升
姚志洪,郝慧君,巫雪梅,赵 斌, 2,蒋阳升
考虑自动驾驶的混合交通流路段阻抗函数
姚志洪1, 2, 3,郝慧君1,巫雪梅1,赵 斌1, 2,蒋阳升1, 2, 3
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 综合交通大数据应用技术国家工程实验室,成都 611756;3. 综合交通运输智能化国家地方联合工程实验室,成都 611756)
为解决未来自动驾驶专用车道的规划设计问题,本文提出了一种自动驾驶车与人工驾驶车混合交通流路段阻抗函数模型。首先,分析了自动驾驶专用车道的设置对混合交通流中车辆跟驰模式的影响;其次,在此基础上,引入微观跟驰驾驶模型,推导了不同自动驾驶车辆渗透率条件下的路段通行能力函数,分析了自动驾驶车辆对路段通行能力的影响;然后,将混合交通流通行能力引入经典的BPR函数,推导了考虑自动驾驶的混合交通流路段阻抗函数模型;最后,设计了数值实验讨论了自由流速度(自由流行程时间)、自动驾驶车辆的渗透率和安全车头时距对路段阻抗的影响。结果表明:(1)当路段流量较小时,自动驾驶车辆的引入对路段阻抗行程时间的影响较小;(2)当自动驾驶车的渗透率为30%时,设置自动驾驶专用车道对行程时间的改善最为明显;(3)当流量较小时,自动驾驶车辆渗透率对路段阻抗行程时间的影响较小,而随着路段流量的增大,自由流速度和自动驾驶车辆渗透率将共同决定路段的行程时间。相关成果可为未来自动驾驶专用车道的规划与设计提供理论支撑。
智能交通;阻抗函数;通行能力;混合交通流;自动驾驶专用道;跟驰模型
0 引 言
自动驾驶汽车作为“交通强国”、“智能汽车”和“新基建”时代的产物,将引领产业生态及商业模式的全面升级与重塑。因此,发展自动驾驶,将有利于提升汽车网联化、智能化水平,进而促进智能交通的发展,对中国推进新型基础设施建设、推动交通强国建设等具有重要意义[1, 2]。
近年来,在国家相关政策的引导下,自动驾驶得到了迅速的发展。但现有实践和研究[3, 4]均表明,实现自动驾驶将是一个漫长的过程,未来将普遍存在自动驾驶车辆和人工驾驶车辆混行的场面[5, 6],因此,在交通系统的规划设计中也需要考虑自动驾驶车辆混入的影响。作为交通规划中不可或缺的部分,交通分配是道路规划的基础,而自动驾驶车辆的应用将重新定义传统的“混合交通流”交通分配方法。随着自动驾驶的快速发展,相关学者[7–10]也对交通规划中的混合交通流交通分配问题进行了相关研究。这些研究将混合交通流中人工驾驶车辆和自动驾驶车辆分别进行分配,采用UE用户均衡模型来描述人工驾驶车辆的分配过程,并考虑到自动驾驶车辆可以进行信息交互,因此,采用SO系统最优模型来描述自动驾驶车辆的分配过程。但这些研究均采用同一个阻抗函数来描述路段流量与行程时间的关系,并未考虑自动驾驶车辆对路段通行能力或阻抗的影响。现有研究表明[11-14],自动驾驶车辆会极大地提高道路的通行能力,进而提升交通系统的运行效率。为解决该问题,Kumar等[15]考虑到自动驾驶车辆对道路通行能力的影响,引入校正参数对BPR阻抗函数进行了修正,在此基础上讨论了混合交通流交通分配问题。但其对阻抗函数的修正过于简单,未从微观驾驶行为层面解析自动驾驶车辆对道路通行能力的影响。Ngoduy等[16]以微观跟驰模型为基础,推导了自动驾驶车辆不同渗透率条件下的基本图,分析了自动驾驶车辆对道路通行能力的影响,但其并未进一步推导路段阻抗函数的具体形式。
综上分析可知,现有对于混合交通流阻抗函数的研究主要存在以下几个问题:① 大多研究在混合交通流交通分配中,并未在阻抗函数中体现自动驾驶车辆对路段阻抗函数的影响;② 部分研究分析了自动驾驶车辆对路段通行能力的影响,并未进一步推导混合交通流条件下的阻抗函数具体形式[16];③ 部分研究考虑了自动驾驶车辆对路段阻抗函数的影响,但其仅引入了比例修正系数,未从影响机理上进行解析和推导具体形式,且并未考虑自动驾驶专用车道设置的影响,仅假设路段所有车道均为自动驾驶专用车道[15]。而现有的实践研究表明[17, 18],在自动驾驶专用道的建设中,一般并不将整个路段的所有车道全部作为自动驾驶专用车道,而往往仅采用部分车道作为自动驾驶专用车道,如某高速公路路段的最内侧车道。因此,本文面向未来自动驾驶环境,研究考虑自动驾驶专用车道影响下的路段阻抗函数模型,为混合交通流环境下的自动驾驶专用车道的规划与选址提供理论基础。
后文具体安排如下:首先,分析了自动驾驶专用车道设置与否对混合交通流中车辆跟驰模式的影响;然后,引入微观跟驰驾驶模型,推导了不同自动驾驶车辆渗透率条件下的路段通行能力函数,分析了自动驾驶车辆对路段通行能力的影响;接着,将混合交通流通行能力引入经典的BPR函数,推导了考虑自动驾驶专用道的混合交通流路段阻抗函数模型;最后,设计数值实验讨论了自由流速度(自由流行程时间)、自动驾驶车辆的渗透率和安全车头时距对路段阻抗的影响。
1 混合交通流阻抗函数模型
1.1 混合交通流跟驰特性分析
1.1.1 跟驰模式分析
如图1所示,本文混合交通流主要由网联自动驾驶车(Connected Automated Vehicle,CAV)和普通人工驾驶车(Human-driven Vehicle,HV)组成。而对于网联人工驾驶车,考虑到其和人工驾驶车辆一致,均由驾驶员驾驶,即其微观驾驶行为相同,因此,本文中未单独考虑网联人工驾驶车辆。此外,当网联自动驾驶车跟驰人工驾驶车时,跟驰过程中并未基于网联通讯功能与前车进行实时交互,此时网联自动驾驶车退化为自动驾驶车(Automated Vehicle,AV)[11, 13]。因此,本文混合交通流中实际含有网联自动驾驶车、自动驾驶车和人工驾驶车。由于不同车辆相对位置的不同,存在4种跟驰模式[19, 20]。

图1 混合交通流路段车辆跟驰示意图
(1)网联自动驾驶车跟驰网联自动驾驶车(C-C)
当前车和后车均为网联自动驾驶车,车辆之间可通过实时通讯共享信息,这种跟驰模式简写为C-C。前车可将自己下一步的纵向驾驶行为(加减速)提前共享给后车,因此,两车之间可实现驾驶行为的同步变化。此时,可认为两辆车组成了一个车队,车队内车辆的驾驶行为一致,可同时进行加减速变化。通常,同一车队内,车辆之间的安全车头时距很小,可用cc表示。
(2)网联自动驾驶车跟驰人工驾驶车(C-H)
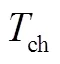
(3)人工驾驶车跟驰网联自动驾驶车(H-C)

(4)人工驾驶车跟驰人工驾驶车(H-H)
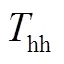
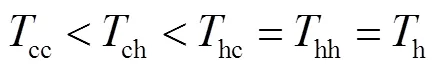

图2 自动驾驶专用道路段车辆跟驰示意图
1.1.2 比例关系分析
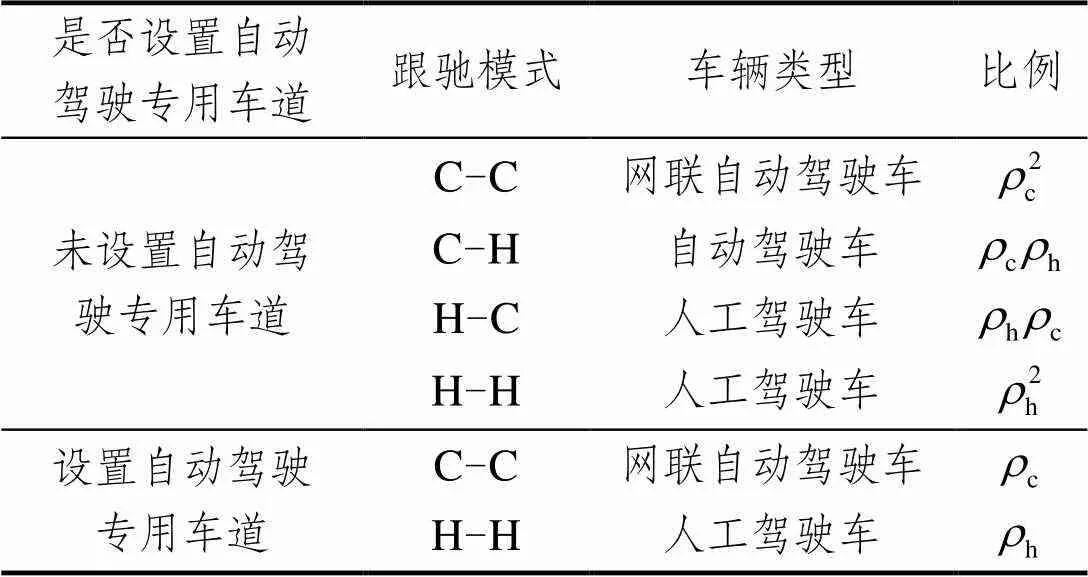
表1 不同跟驰模式比例表
1.2 经典阻抗函数
阻抗函数通常用于交通分配中,其表示路段阻抗(时间、费用等)随道路流量的变化关系。最常见的阻抗函数为BPR阻抗函数,其表示了路段行程时间随路段流量的函数关系,表达式为:
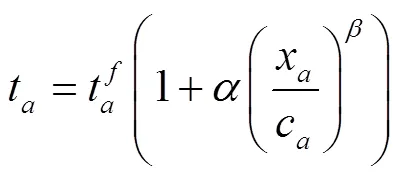
1.3 混合交通流阻抗函数模型
混合交通流条件下,网联自动驾驶车辆的引入,能够提高道路的通行能力,相关研究也证明了网联自动驾驶车辆对道路通行能力有很大的改善作用[11–14]。而由式(1)可知,道路通行能力是阻抗函数的一部分,从该层面分析可知,通行能力的改变也会导致阻抗函数的改变。因此,本节将从网联自动驾驶车辆对道路通行能力的影响入手,基于经典BPR模型推导新的阻抗函数模型。
1.3.1 道路通行能力分析
道路通行能力可由路段的基本图获得,而基本图可由车辆的微观驾驶模型推导得到。以车辆跟驰模型为例来推导路段的基本图模型,通常,车辆的跟驰模型通常可表示为:

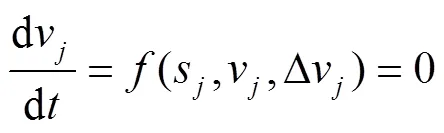


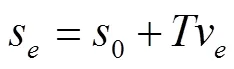
根据稳定交通流的流量-密度-速度关系,可得基本图公式为:

因此,参考文献[16]知取值为1.5s,根据公式(8)绘制路段交通流的基本图,如图3所示。

图3 路段交通流基本图
由图3可知,基本图中存在一个最佳密度,其对应的流量最大,即道路通行能力。进一步分析可知,此时的速度恰好为自由流速度,因此,结合公式(8),路段的通行能力可表示为:
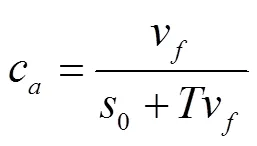
综上分析可知,路段的通行能力与路段的自由流速度、车辆的平均安全车头时距和停车的车头间距有关。其中,停车的车头间距可视为固定值。
1.3.2 不考虑自动驾驶专用车道
由1.1节的分析可知,混合交通流条件下,由于网联自动驾驶车辆的引入,道路的通行能力会发生变化。当不设置自动驾驶专用车道时,道路上存在4种跟驰模式,可用3种不同的安全车头时距进行描述。因此,结合表1,其平均车头时距可表示为:
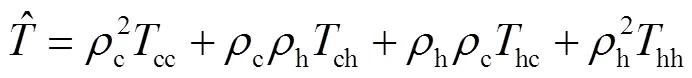
进一步整理可得:
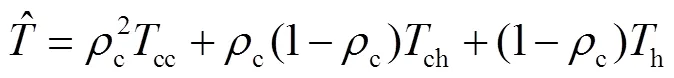
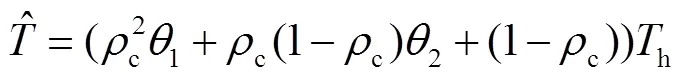


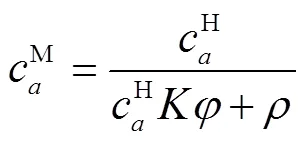


图4 不同自动驾驶车辆渗透率下路段通行能力变化(未设置专用道)

综上,结合公式(1)和(14),可得不设置自动驾驶专用车道的混合交通流阻抗函数为:

1.3.3 考虑自动驾驶专用车道
由1.1节的分析可知,当设置自动驾驶专用车道时,仅存在2种跟驰模式,对应两种不同的安全车头时距。因此,结合表1和公式(11),其平均车头时距可表示为:

同理,结合公式(14),可得到设置自动驾驶专用车道条件下的路段通行能力表达式为:

由图5可知,与不设置自动驾驶专用车道相比,设置专用车道条件下路段通行能力有所增加,其增加的大小与自动驾驶车辆的渗透率有关。当自动驾驶车辆的渗透率为0.75时,路段通行能力增加幅度最大,大约为180 veh/h。因此,实际自动驾驶专用车道选址规划时,应考虑自动驾驶车辆的渗透率。
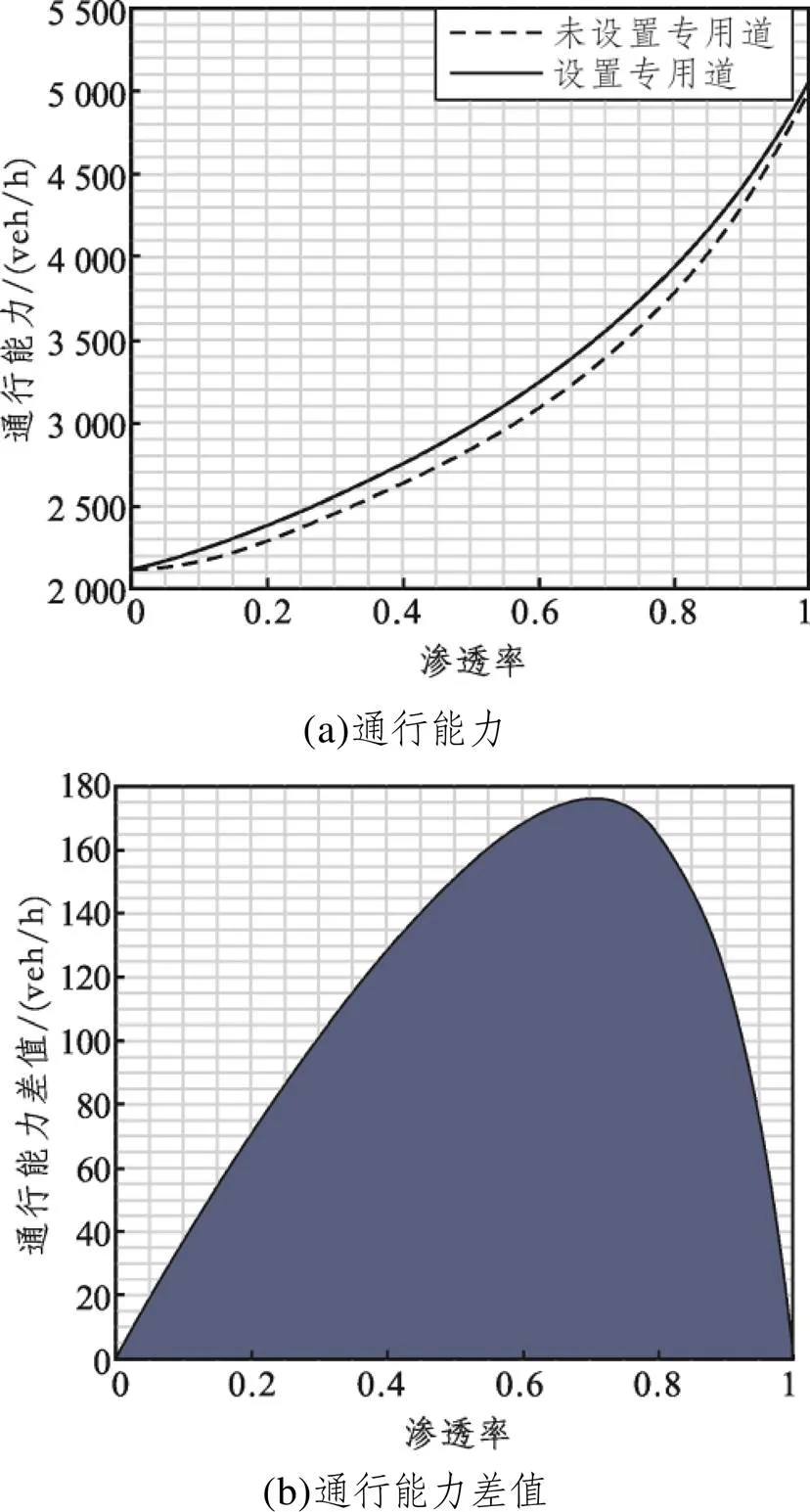
图5 不同自动驾驶车辆渗透率下路段通行能力变化(设置专用道)
同理,结合公式(1)和(18),可得不设置自动驾驶专用车道的混合交通流阻抗函数为:

2 阻抗函数数值分析
考虑到路段自由流速度(自由流行程时间)、自动驾驶车辆的渗透率和安全车头时距是阻抗函数中的重要参数,因此,本节将对这些参数进行敏感性分析,进一步探讨其对路段阻抗的影响。
2.1 自动驾驶车辆渗透率分析


表2 基本参数取值

由图6可知,不管是否设置自动驾驶专用车道,自动驾驶车辆的引入对路段阻抗行程时间均有一定的影响。从图6可知,当流量较小时,如在2 000 veh/h以内时,自动驾驶车辆的引入对路段阻抗行程时间的影响较小;而当流量较大时,如达到4 000 veh/h时,纯人工驾驶车环境(自动驾驶车渗透率为0)路段阻抗行程时间达到3 h,增加了近2倍;而纯自动驾驶车环境(自动驾驶车渗透率为1)路段阻抗行程时间小于1.1 h,仅增加了不到0.1倍。因此,自动驾驶车对拥挤条件下的路段阻抗改善较为明显。进一步可分析设置专用道前后,阻抗函数的变化曲线,如图7所示。
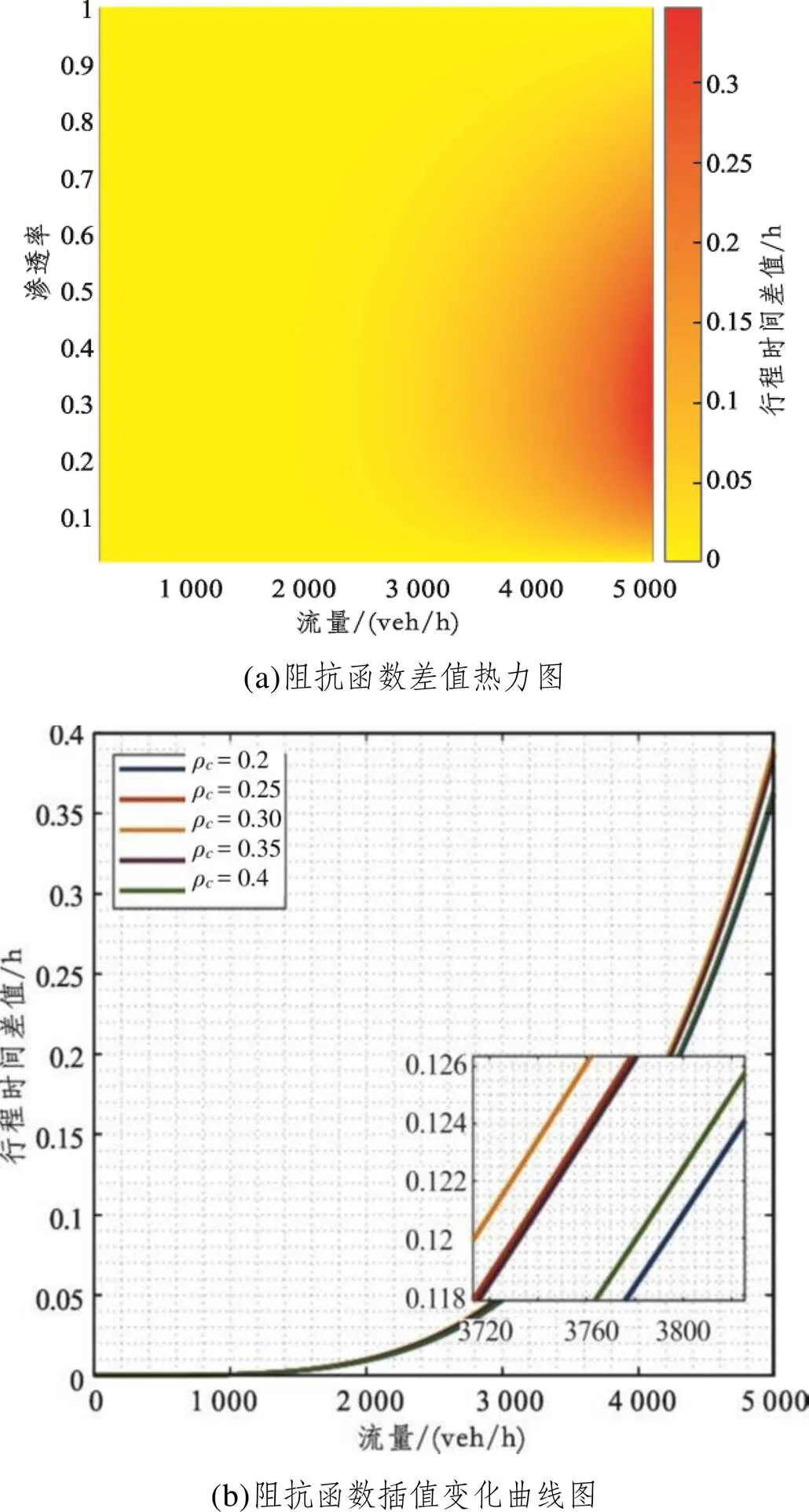
图7 路段阻抗差值分析图
由图7可知,是否设置专用车道对路段阻抗函数有一定的影响。图7(a)的热力图表明,当自动驾驶车的渗透率为30%左右时,设置自动驾驶专用车道与不设置自动驾驶专用车道相比路段阻抗行程时间差值最大,即阻抗减少最大。这表明此时设置自动驾驶专用车道对路段阻抗函数的提升效果更为明显。进一步,以自动驾驶车辆渗透率为20%到40%为例,绘制路段阻抗行程时间差值随流量的变化曲线图,如图7(b)所示。由图7(b)可知,当自动驾驶车辆渗透率为30%时,设置自动驾驶专用车道对行程时间的影响最大,该结果与图7(a)的分析结果一致,即自动驾驶车辆渗透率为30%时,选择设置自动驾驶专用车道对行程时间的改善最为明显。
2.2 自由流速度


由图8(a)可知,当流量较小(1 000 veh/h)且自由流速度相同时,不同自动驾驶车辆渗透率条件下,图中颜色差别不大,即路段行程时间差异较小。但从图8(a)可知,不管自动驾驶车辆的渗透率处于何种水平,路段行程时间总随着自由流速度的增加而逐渐减小。这表明当流量较小时,自动驾驶车辆渗透率对路段阻抗行程时间的影响较小。而当流量逐渐增大时,图8(b)~(f)中同一自由流速度下的纵向颜色带逐渐向右倾斜,这表明随着流量的增大,自由流速度和自动驾驶车辆渗透率将共同决定路段的行程时间。此外,随着路段流量的增大,图8中蓝色区域逐渐减少,而红色部分逐渐增多,这也表明当流量较大时,自动驾驶车辆的应用对路段行程时间的改善更为明显。
2.3 安全车头时距系数
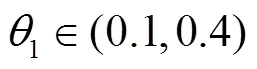
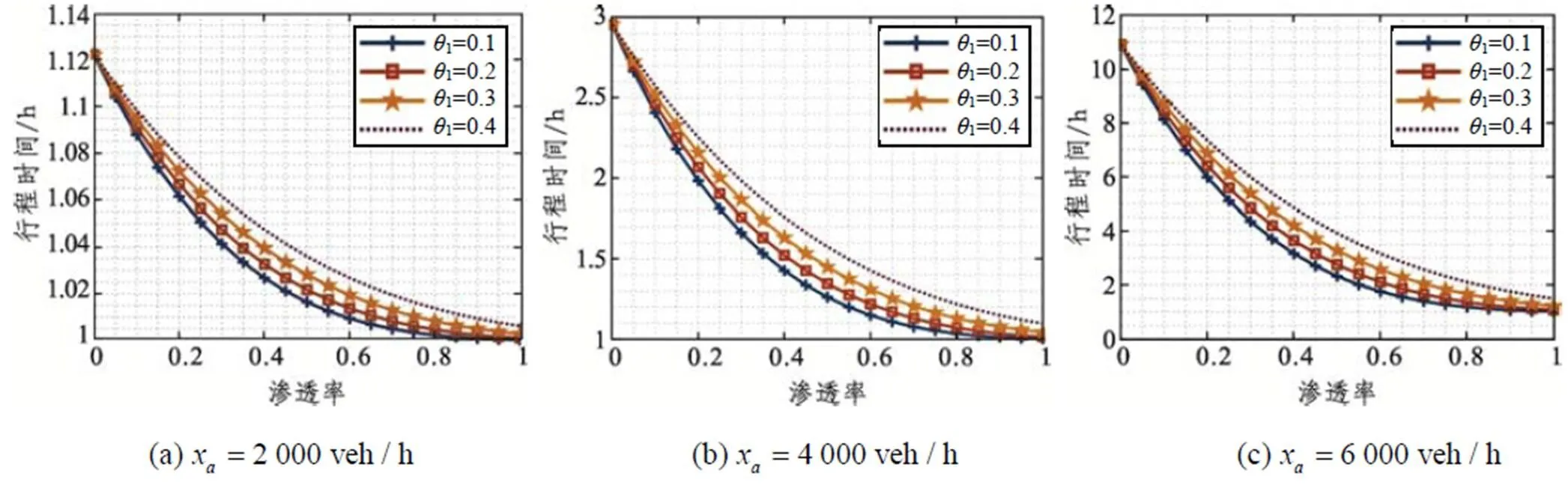
由图9(a)~(c)可知,同一安全车头时距下,路段的行程时间随着渗透率的增加不断减小。且路段行程时间的减小速率随着渗透率的增加逐渐变缓,这表明当混合交通流中自动驾驶车辆达到一定比例时,继续增加自动驾驶车辆的比例,不会使路段行程时间得到明显的改善。图9(d)中显示,随着自动驾驶车辆安全车头间距的减小,路段的行程时间逐渐减小,且3种流量状态下的行程时间变化趋势一样。此外,由图9(d)中不同流量下路段行程时间的变化曲线可知,当路段流量越大,自动驾驶车辆渗透率对路段阻抗行程时间的改善效果越显著。
3 结 论
本文基于微观跟驰驾驶模型和经典的BPR阻抗函数,推导了自动驾驶车与人工驾驶车混合交通流路段阻抗函数模型,通过数值分析可以得出以下结论:
(1)自动驾驶车辆的应用会极大地增加路段的通行能力,与纯人工驾驶车相比,通行能力增加了2.4倍;此外,路段通行能力的提升效果随自动驾驶车辆渗透率增加而增加。
(2)与不设置自动驾驶专用车道相比,设置专用道条件下路段通行能力有所增加,其增加的大小与自动驾驶车辆的渗透率有关。当自动驾驶车辆的渗透率为0.75时,路段通行能力增加幅度最大。
(3)当路段流量较小时,如在2 000 veh/h以内时,自动驾驶车辆的引入对路段阻抗行程时间的影响较小;而当流量较大时,如达到4 000 veh/h时,纯人工驾驶车环境(自动驾驶车渗透率为0)路段阻抗行程时间达到3 h,增加了近2倍。
(4)当自动驾驶车的渗透率为30%左右时,设置自动驾驶专用车道比不设置自动驾驶专用车道路段阻抗行程时间差值最大,即此时设置自动驾驶专用车道对行程时间的改善最为明显。
(5)当流量较小时,自动驾驶车辆渗透率对路段阻抗行程时间的影响较小。而随着流量的增大,路段自由流速度和自动驾驶车辆渗透率将共同决定路段的行程时间。因此,流量较大时,自动驾驶车辆的应用对路段行程时间的改善更为明显。
本文构建了自动驾驶车与人工驾驶车混合环境下的BPR阻抗函数模型,并讨论了自动驾驶专用车道设置对函数模型形式的影响,相关研究成果可为混合交通流环境下的交通分配提供理论基础。文中仅为理论探索研究,相关结果并未采用实际数据验证,因此,后续研究可以结合实际数据校准模型。此外,也可基于本文模型从路网层面讨论混合交通流分配、专用道选址规划等问题,为未来智能网联交通系统的规划设计提供理论支持。
[1] 蒋阳升, 刘梦, 王思琛, 等. 基于跟驰特性的智能网联车混合交通流轨迹重构[J/OL]. 西南交通大学学报, 2021: 1-9[2021-07-20]. http: //kns. cnki. net/kcms/detail/51. 1277. U. 20210415. 1048. 012. html.
[2] 祁宏生, 应雨燕, 林俊山, 等. 混合自动驾驶场景多换道需求下的主动间隙适配和换道序列规划[J/OL]. 交通运输工程与信息学报, 2021: 1-19[2021-06-22]. https: //doi. org/10. 19961/j. cnki. 1672-4747. 2021. 04. 031.
[3] YAO Z, WANG Y, LIU B, et al. Fuel consumption and transportation emissions evaluation of mixed traffic flow with connected automated vehicles and human-driven vehicles on expressway[J]. Energy, 2021, 230: 120766.
[4] ARVIN R, KHATTAK A J, KAMRANI M, et al. Safety evaluation of connected and automated vehicles in mixed traffic with conventional vehicles at intersections[J]. Journal of Intelligent Transportation Systems, 2021, 25(2): 170-187.
[5] 徐桃让, 姚志洪, 蒋阳升, 等. 智能网联车环境下考虑反应时间影响的基本图模型[J]. 公路交通科技, 2020, 37(8): 108-117.
[6] 蒋阳升, 胡蓉, 姚志洪, 等. 智能网联车环境下异质交通流稳定性及安全性分析[J]. 北京交通大学学报, 2020, 44(1): 27-33.
[7] BAHRAMI S, ROORDA M J. Optimal traffic management policies for mixed human and automated traffic flows[J]. Transportation Research Part A: Policy and Practice, 2020, 135: 130-143.
[8] BAGLOEE S A, SARVI M, PATRIKSSON M, et al. A mixed user-equilibrium and system-optimal traffic flow for connected vehicles stated as a complementarity problem[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(7): 562-580.
[9] ZHANG K, NIE Y. Mitigating the impact of selfish routing: an optimal-ratio control scheme(ORCS)inspired by autonomous driving[J]. Transportation Research Part C: Emerging Technologies, 2018, 87: 75-90.
[10] WANG J, PEETA S, HE X. Multiclass traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles[J]. Transportation Research Part B: Methodological, 2019, 126: 139-168.
[11] YAO Z, HU R, WANG Y, et al. Stability analysis and the fundamental diagram for mixed connected automated and human-driven vehicles[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 533: 121931.
[12] TALEBPOUR A, MAHMASSANI H S. Influence of connected and autonomous vehicles on traffic flow stability and throughput[J]. Transportation Research Part C: Emerging Technologies, 2016, 71: 143–163.
[13] QIN Y, WANG H, NI D. LWR Model for traffic flow mixed with CACC vehicles[J/OL]. Transportation Science, 2021: 1-25[2021-06-29]. https: //doi. org/10. 1287/trsc. 2021. 1057.
[14] ZHOU J, ZHU F. Modeling the fundamental diagram of mixed human-driven and connected automated vehicles[J]. Transportation Research Part C: Emerging Technologies, 2020, 115: 102614.
[15] KUMAR A, GUHATHAKURTA S, VENKATACHALAM S. When and where should there be dedicated lanes under mixed traffic of automated and human-driven vehicles for system-level benefits?[J]. Research in Transportation Business & Management, 2020, 36: 100527.
[16] NGODUY D, HOANG N H, VU H L, et al. Multiclass dynamic system optimum solution for mixed traffic of human-driven and automated vehicles considering physical queues[J]. Transportation Research Part B: Methodological, 2021, 145: 56-79.
[17] YE L, YAMAMOTO T. Impact of dedicated lanes for connected and autonomous vehicle on traffic flow throughput[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 512: 588-597.
[18] RAZMI RAD S, FARAH H, TAALE H, et al. Design and operation of dedicated lanes for connected and automated vehicles on motorways: aconceptual framework and research agenda[J]. Transportation Research Part C: Emerging Technologies, 2020, 117: 102664.
[19] YAO Z, XU T, JIANG Y, et al. Linear stability analysis of heterogeneous traffic flow considering degradations of connected automated vehicles and reaction time[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 561: 125218.
[20] QIN Y, WANG H. Cell transmission model for mixed traffic flow with connected and autonomous vehicles[J]. Journal of Transportation Engineering, Part A: Systems, 2019, 145(5): 04019014.
[21] YAO Z, HU R, JIANG Y, et al. Stability and safety evaluation of mixed traffic flow with connected automated vehicles on expressways[J]. Journal of Safety Research, 2020, 75: 262-274.
[22] NEUHOLD R, FELLENDORF M. Volume delay functions based on stochastic capacity[J]. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2421(1): 93-102.
[23] TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations[J]. Physical Review E, 2000, 62(2): 1805- 1824.
[24] BANDO M, HASEBE K, NAKAYAMA A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51: 1035-1042.
[25] JIANG R, WU Q, ZHU Z. Full velocity difference model for a car-following theory[J]. Physical Review E, 2001, 64(1): 017101.
Cost Function of Mixed Traffic Flow with Autonomous Driving
YAO Zhi-hong1, 2, 3, HAO Hui-jun1, WU Xue-mei1, ZHAO Bin1, 2, JIANG Yang-sheng1, 2, 3
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China; 3. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China)
To solve the planning and design problems of automated dedicated lanes (ADLs), this study proposes a cost function model for mixed traffic flow of connected automated vehicles (CAVs) and human-driven vehicles. First, the influence of the ADL setting on car-following modes in mixed traffic flow is analyzed. Second, a car-following driving model is adopted to derive the traffic capacity function under different penetration rates of CAVs, and the effects of CAVs on traffic capacity are analyzed. The capacity of mixed traffic flow is then introduced into the classic Bureau of Public Roads function, and a cost function model of mixed traffic flow that considers autonomous driving is derived. Finally, numerical experiments are conducted to examine the effects of free-flow velocity (free travel time), penetration rates of CAVs, and safe headway on the cost function. The results showed that: (1) when the traffic volume was low, the effects of the application of CAVs on travel time were small; (2) when the penetration rate of CAVs was 30%, the improvement in travel time was the most obvious when the ADL was set; and (3) when the traffic volume was low, the penetration rates of CAVs had little effect on the travel time. With an increase in traffic volume, the free-flow velocity and penetration rates of CAVs jointly determine the travel time. The relevant findings can provide theoretical support for future planning and design of automated dedicated lanes.
intelligent transportation; cost function; traffic capacity; mixed traffic flow; automated dedicated lane; car-following model
U491.1
A
10.19961/j.cnki.1672-4747.2021.07.024
1672-4747(2021)04-0001-12
2021-07-17
2021-07-20
2021-07-22
2021-07-17~07-19; 07-19~07-20
国家自然科学基金项目(52002339);四川省科技计划项目(2021YJ0535,2020YFH0026);广西科技计划项目(2021AA01007AA);中央高校基本科研业务费专项资金资助项目(2682021CX058)
姚志洪(1991—),男,博士,助理教授,研究方向为智能网联交通系统建模、交通信号控制,E-mail:zhyao@swjtu.edu.cn
蒋阳升(1976—),男,教授,博导,研究方向为交通系统优化,E-mail:jiangyangsheng@swjtu.edu.cn
姚志洪,郝慧君,巫雪梅,等. 考虑自动驾驶的混合交通流路段阻抗函数[J]. 交通运输工程与信息学报,2021, 19(4): 1-12.
YAO Zhi-hong, HAO Hui-jun, WU Xue-mei, et al. Cost Function of Mixed Traffic Flow with Autonomous Driving[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 1-12.
(责任编辑:李愈)
