高温后混凝土初始压实阶段应力-应变关系

王 磊，赵燕茹，郝 松

(1.内蒙古工业大学理学院，呼和浩特 010051；2.内蒙古工业大学土木工程学院，呼和浩特 010051； 3.内蒙古自治区土木工程结构与力学重点实验室，呼和浩特 010051；4.海南三亚湾新城开发有限公司，三亚 572000)

0 引 言

混凝土结构在经历火灾或高温作用后，为防止发生二次破坏以及为抢运重要物资赢得时间，同时也为后期的修复加固方案和安全施工方案的制定提供依据，往往需要对受损结构的真实受力状态重新进行评估，预判一些薄弱点进行临时支护[1-2]。因此，需要对经历不同温度后混凝土的应力-应变关系进行研究。为表征高温后混凝土的单轴压缩应力-应变关系，学者们建立许多模型，常用的有过镇海[3]提出的分段模型及其修正模型[4-7]，以及一些其他的多项式或分式拟合的分段函数模型[8-9]。这些模型虽然形式简单使用方便，但均未能考虑高温后混凝土的初始压实现象[10]。这种现象是由于高温损伤后混凝土基体内部的空隙和微裂缝在加载初期被压实所导致的，而且这种初始压实现象会随着温度的增加越来越显著。

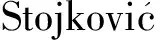
本文将基于混凝土单轴压缩试验，研究高温后混凝土的应力-应变关系，通过定义压实系数和密实程度指标，评价高温后混凝土的密实程度，探讨混凝土初始压实阶段随温度的变化规律，最后采用统一形式的分段函数建立考虑初始压实阶段的单轴压缩应力-应变全曲线方程，并分析高温后混凝土的压缩损伤全过程。为高温后混凝土的力学性能和变形性能研究提供理论依据。

1 试验方法

1.1 原材料及配合比

水泥采用42.5普通硅酸盐水泥；细骨料采用天然水洗河砂，细度模数为2.45，密度为2 650 kg/m3；粗骨料选用碎石，粒径为5～20 mm，密度为2 800 kg/m3；拌合水采用自来水。混凝土强度等级为C30，水胶比为0.45，砂率为0.35，配合比为m(水泥) ∶m(水) ∶m(砂子) ∶m(石子)=489 ∶220 ∶591 ∶1 160。试件为100 mm×100 mm×300 mm的棱柱体，每组3块，共5组试件，标准养护28 d。

1.2 高温试验

高温试验采用硅碳棒加热的GW-1000型高温炉，最高温度可达1 000 ℃，额定功率30 kW。升温制度依据ISO-834规定的火灾标准升温曲线[18]进行。试验设置5个目标温度，分别为20 ℃(室温)、200 ℃、400 ℃、600 ℃、800 ℃，当达到目标温度后恒温120 min，然后自然冷却到室温。

1.3 抗压试验

采用微机控制电液伺服万能试验机加载，试验过程按照GB/T 50081—2019《混凝土物理力学性能试验方法标准》的规定执行，加载过程采用位移控制，加载速率为0.05 mm/min。采用应变片进行应变测试，在棱柱体试件相对的两个测面上，沿竖向中线各粘贴一个长度为100 mm应变片，用于测试轴向应变；在棱柱体试件另外的一个侧面上，沿着水平中线粘贴一个长度为50 mm的应变片，用于测试横向应变。应变片电阻值为(120.5±0.2) Ω，灵敏系数为(2.06±1)%。

2 试验结果

2.1 应力-应变关系曲线

图1为高温后混凝土单轴压缩应力-应变曲线随温度的变化趋势。由图1(a)可知，随温度的增加，应力-应变曲线由陡峭逐渐趋于扁平，峰值点不断下降和右移，初始斜率不断减小。与常温相比，200 ℃和400 ℃时，峰值应力下降幅度较小，在20%～25%，峰值应变与20 ℃时相差不大，混凝土在应力上升阶段的弹性模量与20 ℃相比仅有小幅下降，而在应力下降阶段，曲线迅速回落，混凝土整个压缩损伤破坏过程呈明显的脆性特征。对于600 ℃和800 ℃，峰值应力大幅减小，降幅约为60%～90%，峰值应变迅速增加，最大增幅约为160%，同时应力-应变曲线上升阶段的弹性模量大幅减小，曲线下降阶段的下降速度明显减缓，混凝土整个压缩损伤破坏过程呈延性特征。

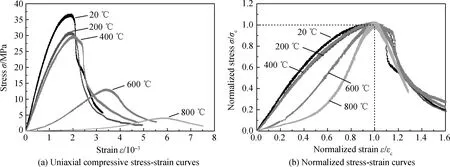
图1 高温后混凝土单轴压缩应力-应变曲线Fig.1 Uniaxial compressive stress-strain curves of concrete after high temperature

图1(b)给出了用峰值应力和峰值应变分别对应力和应变做归一化处理之后的曲线。由图1(b)可知，曲线上升阶段在不同温度下存在明显差异。20 ℃、200 ℃和400 ℃时，三条曲线非常接近，且存在明显的线性增长阶段，切线模量随荷载的增加逐渐减小，反映出混凝土随荷载的增加损伤在逐渐加剧。当温度达到600 ℃和800 ℃时，曲线上升段呈凹曲向上的增长趋势，切线模量随荷载的增加先增加后减小，同时伴随有较大的压缩应变。这是因为混凝土的高温劣化，使其内部集聚了大量微裂缝和孔洞，在荷载作用下这些微裂缝和孔洞的首先发生压实和闭合，呈现出切线模量增加的趋势，这个过程为混凝土的初始压实过程。当基体被完全压实后，继续增加荷载，基体才开始损伤破坏，呈现出切线模量减小的趋势。而且，温度越高，混凝土的初始压实阶段就越明显。

2.2 压实系数和相对密实度

图2 应力-应变曲线初始压实阶段示意图Fig.2 Schematic diagram of initial compaction stage of the stress-strain curve

为描述混凝土的初始压实阶段，先假设在应力-应变曲线上升过程中当切线模量达到最大值时，混凝土被完全压实。最大切线模量称为临界压实模量，记作Ecr，所对应的应力-应变曲线上的点称为临界压实点，记作(εcr，σcr)，应力-应变曲线初始压实阶段如图2所示。本文利用Origin软件对应力-应变曲线先进行高阶多项式拟合再求微分，分别确定初始弹性模量E0和临界压实模量Ecr，最终确定临界压实点，结果如表1所示。

由表1可知，初始弹性模量和临界压实模量均随温度的增加而逐渐减小。200 ℃和400 ℃时减小幅度约为30%，600 ℃和800 ℃时减小幅度约为80%。临界压实模量相对于初始弹性模量均有一定幅度的提高，这说明不论是室温还是高温条件下，混凝土材料均存在初始压实现象。

为表征不同温度后混凝土的初始压实阶段，文本分别定义了压实系数φ和相对密实度Φ，即：

(1)

(2)

式中:φ为混凝土初始压实过程中弹性模量的总增长率，0≤φ≤1，其值越大，表明混凝土的压实效果越明显；Φ是评价混凝土密实程度的一个综合指标，0≤Φ≤1，它不仅与弹性模量的总增长率有关，还与压实阶段占应力-应变曲线上升段的比例有关，在本文中该比例用σcr/σc来近似表示。相对密实度Φ的值越大，表明混凝土材料的密实程度越高，初始压实阶段越不明显；其值越小，表明混凝土材料越疏松，初始压实阶段也越显著。

表1 高温后混凝土临界压实点的参数Table 1 Parameters of critical compaction point of concrete after high temperature

图3 高温后混凝土压实系数和相对密实度Fig.3 Compaction coefficient and relative compactness of concrete after high temperature

图3给出了压实系数和相对密实度随温度的变化规律。由图3可知，20 ℃时，压实系数φ仅为0.06，说明弹性模量的总增长率很小，而相对密实度Φ高达0.99，说明此时混凝土的密实程度很高。200 ℃和400 ℃时，虽然压实系数φ有一定程度提高，但是相对密实度Φ仍保持在0.94以上，说明此时混凝土基体密实程度仍然很高。结合图1分析可知，温度为20～400 ℃时，应力-应变曲线的初始压实阶段几乎可以忽略。当温度从600 ℃增大到800 ℃时，此时压实系数φ增大到0.92，趋近于1，说明弹性模量的总增长率显著增加，同时压实过程占应力-应变曲线上升段比例也显著提高，因此计算的相对密实度Φ下降至0.29，此时混凝土内部疏松劣化严重，孔隙度增加，结合图1分析可知，此时混凝土基体密实程度迅速下降，在压缩荷载作用下有着明显的初始压实阶段，因此初始压实阶段在应力-应变曲线研究中不可忽略。

2.3 横向应变和体应变

在小变形条件下，混凝土的体应变εv为：

εv=2εl+ε

(3)

式中：εl为混凝土横向应变；ε为混凝土轴向应变。图4为不同温度后横向应变和体应变随应力变化曲线，由图4可知，横向应变随应力的增大向负方向逐渐增加，表明试件发生横向膨胀变形。体应变随应力的增大，先正向增加，然后又向负方向一直增加，直到试件破坏，这说明在加载初期，试件首先被压缩，当荷载继续增大时，试件的总体积才发生膨胀直到破坏。

由图4可知，温度对横向应变和体应变曲线的发展趋势产生了重要影响。首先，20～400 ℃时横向应变和体应变的数值要明显小于600 ℃和800 ℃时的值。其次，从曲线上升阶段的特征来看，20～400 ℃时，横向应变和体应变曲线存在明显的线性增长阶段；600～800 ℃时，横向应变和体应变曲线呈非线性增长趋势。最后，从临近破坏时的变形特征来看，20 ℃时，横向应变和体应变曲线在应力接近峰值时才会突然向负方向迅速增长，形成明显的转折点，体现出脆性破坏特征；200 ℃和400 ℃时，横向应变和体应变曲线的这种转折会更早出现，但转折过程变得更平滑，说明温度在改变试件破坏的脆性特征；600 ℃和800 ℃时，横向应变曲线变得非常平滑，没有明显的转折过程，类似地，体应变曲线的在加载初期就已发生转折，且转折过程更缓和平滑，体现出明显的延性特征。

20～400 ℃时，体应变曲线表明混凝土在加载初期体积被压缩，但由于此时混凝土密实程度较高，体积压缩量相对较小，因此，初始压实过程不是很显著。而600 ℃和800 ℃时，体应变曲线表明混凝土在加载初期体积被迅速压缩，存在一个明显的压实过程，说明混凝土基体已经疏松劣化非常严重。

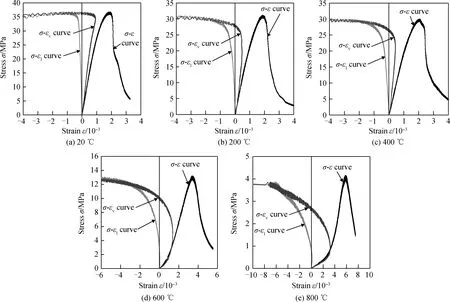
图4 不同温度后横向应变和体应变随应力变化曲线Fig.4 Stress-lateral strain and volumetric strain curves of concrete after different temperatures

3 高温后混凝土应力-应变关系全曲线方程

为了准确表征不同温度后混凝土单轴压缩应力-应变曲线的初始压实阶段，同时，考虑到归一化处理后各个温度下应力-应变曲线的下降段差异性不显著。本文采用过镇海模型[3]中的分式表达式，并对其进行改进，分别拟合应力-应变曲线的上升段和下降段，建立不同温度后混凝土单轴压缩应力-应变关系全曲线方程：

(4)

式中：a1和a2分别是上升段和下降段所对应的拟合参数；σc和εc分别是峰值应力和峰值应变。不同温度下a1和a2的拟合结果见表2，由表2可知参数的拟合度较高，说明该全曲线方程与试验值吻合较好，而且该方程的形式简洁，参数较少，方便工程应用。

由表2可知，拟合参数a1随温度的增加逐渐增大，而a2随温度的增加逐渐减小。由公式(4)的性质可知，参数a反映曲线的凹曲程度，因此，a1增大表征了初始压实阶段随温度增加逐渐显著，而a2减小表征了应力-应变曲线下降段的脆性破坏特征随温度的增加逐渐向延性特征转变。最后，a1和a2分别与温度T进行拟合，得到其随温度变化的公式为：

(5)

表2 高温后混凝土应力-应变全曲线方程的拟合参数Table 2 Fitting parameters of stress-strain relationship of concrete after high temperature

4 高温后混凝土单轴压缩损伤分析

根据损伤力学中Lemaitre应变等价性理论，荷载损伤的名义应力σ与有效应力σ′之间存在如下关系：

σ=(1-D)σ′=(1-D)E′ε

(6)

(7)

联立公式(4)、(6)和(7)可得荷载损伤度的表达式为：

(8)

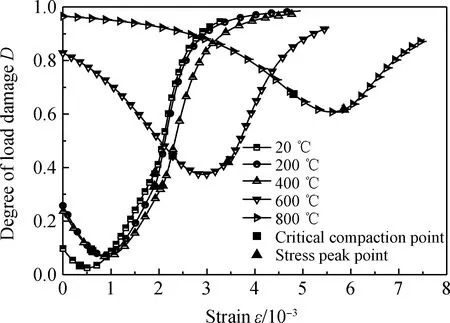
图5 不同温度下荷载损伤度D随应变的变化曲线Fig.5 Curves of load damage degree D with strain at different temperatures

绘制不同温度下荷载损伤度D随应变的发展趋势，如图5所示。从图5可以看出，荷载损伤度曲线与通常情况下的变化趋势略有不同，并不是从0开始逐渐增加并趋近于1，而是存在一个初始损伤度，之后荷载损伤度随应变增加先减小再增大，并逐渐趋近于1。这是因为本文建立的应力-应变全曲线方程考虑了初始压实阶段，高温后混凝土初始状态的疏松程度广义上可以看作是已有的损伤。随着荷载的增加，疏松的试件首先被压实，荷载损伤度逐渐减小，这个过程从广义上可以理解为一个损伤修复的过程。当压实阶段结束之后，荷载继续增加，试件逐渐损伤并最终发生破坏，对应荷载损伤度又重新增长并趋近于1。

从图5还可知，荷载损伤度曲线的最小值始终大于0，且始终位于临界压实点和峰值点之间。这正是由于初始压实阶段的存在，使得临界压实模量Ecr的延长线与应变轴的截距γ0不为0。因此，应力-应变曲线上其任意点的割线模量Esec均小于临界压实模量Ecr，导致基于临界压实模量所计算的广义荷载损伤度D始终大于0。由于初始压实阶段的存在，应力-应变曲线上割线模量的最大值Esecmax，也就是损伤度最小值，只能位于临界压实点和峰值点之间，如图2所示。

从图5中还可以看出，温度较低(20～400 ℃)时，荷载损伤度曲线从开始到临界压实点的过程非常短暂，说明初始压实阶段的影响较小，荷载损伤度的最小值趋近于0，然后荷载损伤度全曲线随应变增加迅速上升并趋近于1，整个损伤过程呈脆性特征。而当温度较高(600 ℃和800 ℃)时，荷载损伤度曲线的下降过程越来越显著，同时伴随有较大的压缩应变，也正是由于初始压实阶段产生的较大压缩应变，使得荷载损伤度的数值保持在一个较高的区间内，荷载损伤度曲线变得非常平缓，整个损伤过程呈现延性特征。

5 结 论

(1)当温度为200 ℃和400 ℃时，混凝土的高温损伤相对较小，峰值应力下降幅度约为20%～25%，峰值应变与20 ℃时相差不大，初始弹性模量与临界压实模量均下降30%左右。当温度为600 ℃和800 ℃时，混凝土高温损伤迅速增加，峰值应力降幅约为60%～90%，峰值应变迅速增加，最大增幅约为160%，初始弹性模量和临界压实模量下降幅度约为80%。

(2)当温度为20 ℃、200 ℃和400 ℃时，混凝土的压实系数相对较小，而相对密实度很高，均在0.94以上，此时混凝土的初始压实阶段几乎可以忽略。当温度为600 ℃和800 ℃时，压实系数逐渐增大并趋近于1，相对密实度迅速下降，800 ℃时下降至0.29，此时混凝土具有明显的初始压实阶段，因此建议600 ℃以后，高温后混凝土的单轴压缩应力-应变关系应考虑初始压实阶段。

(3)本文建立的应力-应变全曲线方程，拟合度高且参数较少。基于全曲线方程计算的荷载损伤度曲线存在一个初始损伤度，此时的损伤度是将高温后混凝土的初始疏松状态看作一种广义损伤。同时，荷载损伤度曲线在初始压实阶段是一个下降过程，此时可将初始压实阶段理解为一个损伤修复的过程。